星球车锥齿轮式差速机构低温传动适应性设计

赵志军 林云成 袁宝峰

(北京空间飞行器总体设计部 空间智能机器人系统技术与应用北京市重点实验室，北京 100094)

锥齿轮式差速机构结构紧凑，对星球车载荷布局约束少，我国月球车和火星车均采用该种差速机构。但其内部存在多个锥齿轮互相啮合，使得该种传动方式对温度变化较为敏感，低温时易出现锥齿轮传动卡滞现象。在月球、火星等温度变化范围大的星球表面工作时(高低温差可达近百摄氏度)，为了防止锥齿轮式差速机构传动回差大导致星球车车体俯仰晃动大，同时防止其传动回差小导致低温传动卡滞，有必要开展锥齿轮式差速机构低温传动适应性设计，提出传动回差与传动轴设计参数之间的数学关系，保证其在低温环境中传动平稳无卡滞且启动力矩较常温时无明显变化。

目前，高低温环境中齿轮传动研究多集中在单对直齿轮副的传动精度、系统动力学特性等方面，且研究以理论分析为主[1-2]，针对锥齿轮式差速机构低温传动适应性设计的研究及工程应用鲜有报道。因此，结合我国祝融号火星车工程实施需求，开展锥齿轮式差速机构低温传动适应性设计及其应用研究具有重要意义。

本文结合祝融号火星车锥齿轮式差速机构传动设计，提出了锥齿轮式差速机构传动回差估算数学模型，利用差速机构工程样机对回差估算数学模型的正确性进行验证。根据回差估算数学模型确定祝融号火星车差速机构的传动回差值，并在常温常压、低温环境下对该差速机构的传动性能进行测试。测试结果表明：常温及低温条件下差速机构传动平稳无卡滞、常温和低温启动力矩较为接近，传动回差估算数学模型可指导锥齿轮式差速机构的工程化设计。

1 锥齿轮式差速机构传动方案

星球车(如月球车、火星车)移动装置多采用Rocker-Bogie构型[3-7]，该构型具有良好的地形适应能力和越障能力，其主要由主摇臂、副摇臂、差速机构等组成。差速机构在Rocker-Bogie构型中具有重要作用：①连接左右两侧主摇臂实现它们之间的反向同步联动，以提高移动装置的地形适应能力；②承载车体绕左右两侧主摇臂转动轴线产生的俯仰弯矩，阻止车体俯仰倾翻。截至目前，国内外提出了多种星球车用差速机构设计方案，例如：美国勇气号、机遇号火星车移动装置采用行星减速器式差速机构[8]，好奇号火星车移动装置采用连杆式差速机构[9]；我国玉兔号月球车移动装置、祝融号火星车移动装置采用锥齿轮式差速机构[10]。

本文以祝融号火星车为例，其锥齿轮式差速机构采用4个锥齿轮啮合传动，传动原理及设计模型如图1所示。为减小差速机构的质量和体积，4个锥齿轮中2个为大锥齿轮、2个为小锥齿轮；在输出轴上设计有旋转变压器，用于测量左右两侧主轴之间的相对转角，可反演火星车行驶过程中路面的起伏程度。

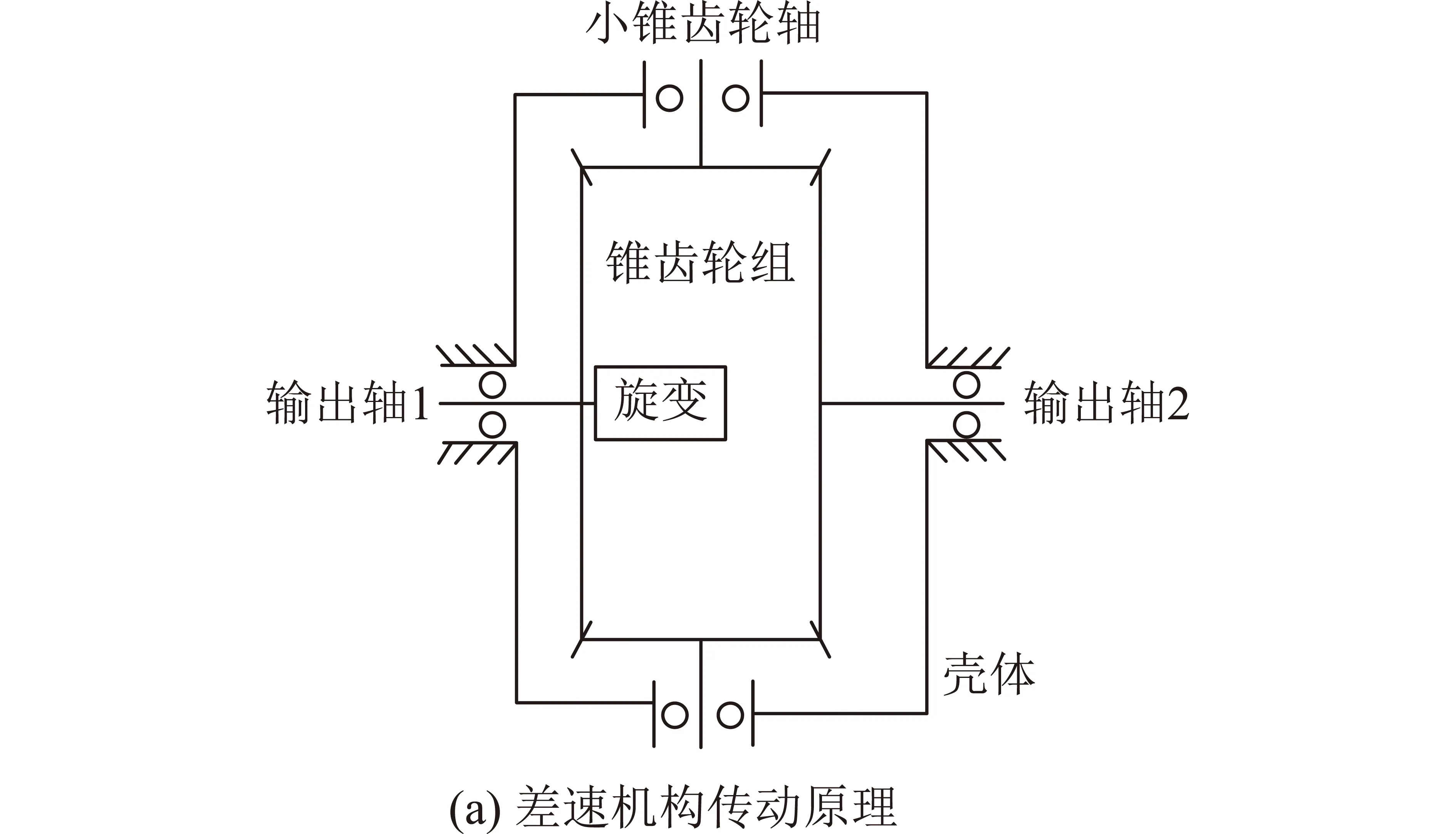
图1 差速机构传动原理及设计模型

如图2所示，祝融号火星车的差速机构位于主轴中间，左右2个输出轴(输出轴1和输出轴2)通过主轴与车体两侧的悬架固连，使得左右两侧悬架可实现反向联动，提高火星车移动过程中车轮对不平坦地形的适应能力。差速机构壳体与车体固连，用于承载车体的俯仰弯矩。

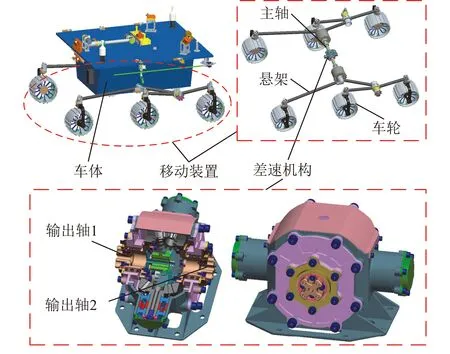
图2 祝融号火星车移动装置及差速机构示意

2 差速机构低温传动适应性设计

锥齿轮式差速机构的4个锥齿轮轴线交叉，低温环境下壳体收缩会导致4个锥齿轮之间的啮合侧隙变小，如果常温时侧隙控制不合理，低温时锥齿轮之间极可能发生卡滞。若能在设计阶段预测温度变化对侧隙的影响，便可在产品实现时预留适当侧隙，以补偿低温侧隙收缩，保证低温时侧隙仍大于零，实现锥齿轮低温传动不卡滞。

2.1 锥齿轮传动回差估算数学模型

影响锥齿轮传动回差的主要因素为壳体冷缩、大锥齿轮及小锥齿轮分度圆冷缩、大锥齿及小锥齿轮回转轴轴向冷缩等。壳体、锥齿轮、锥齿轮回转轴等部件的关键尺寸及相对位置关系，如图3所示。其中：a为壳体内侧小锥齿轮安装面之间的距离；b为壳体内侧大锥齿轮安装面之间的距离；d1为大锥齿轮分度圆直径；d2为小锥齿轮分度圆直径；l1为大锥齿轮分度圆距离其在壳体上安装位置内侧的距离(大锥齿轮分体设计，l1=l11+l12，l11为大锥齿轮转轴的长度，l12为大锥齿轮分度圆距其与转轴连接处的距离)；l2为小锥齿轮分度圆与其壳体安装位置内侧之间的距离；δ1为大锥齿轮分锥角；δ2为小锥齿轮分锥角。

大、小锥齿轮分度圆沿各自回转轴线移动，导致锥齿轮啮合副侧隙发生变化。如图3所示，将大、小锥齿轮分度圆沿各自轴线的移动量在啮合面公法线及啮合线方向上进行分解，r1为大锥齿轮移动量ΔS1在齿轮啮合面公法线方向上的分量，t1为大锥齿轮移动量ΔS1在齿轮啮合线方向上的分量，r2为小锥齿轮移动量ΔS2在齿轮啮合面公法线方向上的分量，t2为小锥齿轮移动量ΔS2在齿轮啮合线方向上的分量，可得

图3 锥齿轮啮合间隙分析示意

(1)

传动回差分析时，涉及到结构件的基本尺寸及其材料的线膨胀系数。以祝融号火星车差速机构为例进行传动回差分析，其壳体材料为铝合金7A09，齿轮材料为高强度不锈钢CF170，输出轴材料为钛合金TC4R，3种材料的近似线膨胀系数如表1所示，影响差速机构锥齿轮传动回差的零部件设计参数值如表2所示。

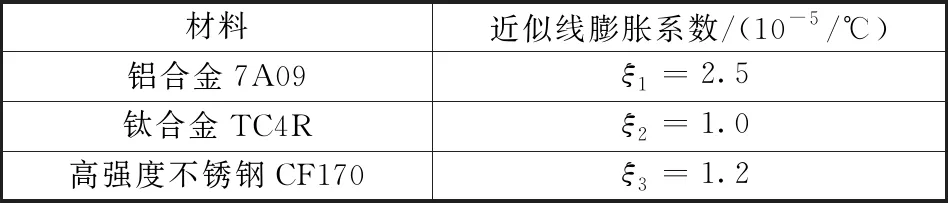
表1 材料近似线膨胀系数

表2 差速机构零部件设计参数值

当环境温度从室温降到低温时(温度变化为ΔT)，差速机构单个大锥齿轮分度圆沿其回转轴线向壳体中心收缩的距离为

ΔL1=[ξ1b/2-(ξ2l11+ξ3l12)]ΔT

(2)

大锥齿轮分度圆直径冷缩量为

Δd1=ξ3d1ΔT

(3)

单个小锥齿轮分度圆沿其回转轴线向壳体中心收缩的距离为

ΔL2=[ξ1a/2-ξ3l2]ΔT

(4)

小锥齿轮分度圆直径冷缩量为

Δd2=ξ3d2ΔT

(5)

因此，在大锥齿轮轴线方向，大锥齿轮分度圆相对于小锥齿轮分度圆接近的距离为

ΔS1=ΔL1-Δd2/2=

[ξ1b/2-(ξ2l11+ξ3l12)-ξ3d2/2]ΔT

(6)

同理，在小锥齿轮轴线方向，小锥齿轮分度圆相对于大锥齿轮分度圆接近的距离为

ΔS2=ΔL2-Δd1/2=

[ξ1a/2-ξ3l2-ξ3d1/2]ΔT

(7)

低温冷缩导致锥齿轮啮合副在啮合面公法线方向的侧隙减小量为r1+r2，导致锥齿轮啮合副在啮合线方向上的相对错动量为t1-t2。定义锥齿轮每个齿的两侧齿面上啮合线之间的夹角为θ(分度圆位置)，则啮合副相对错动引起的侧隙变化约为2(t1-t2)tan(θ/2)。因此，低温冷缩引起的沿啮合面公法线方向的侧隙减小量为

Δjn=r1+r2+2(t1-t2)tan(θ/2)

(8)

类比圆柱齿轮径向侧隙与圆周向侧隙关系，可计算出锥齿轮圆周向侧隙减小量为

Δjc=2Δjntanα=

2[r1+r2+2(t1-t2)tan(θ/2)]tanα

(9)

由圆周向侧隙减小量可求得单侧大锥齿轮回差减小量为

(10)

将表2中差速机构参数代入式(1)和式(6)～(10)，可求得当温度降低90 ℃(差速机构从室温25 ℃降低到低温工作温度-65 ℃)时，差速机构单侧锥齿轮副(输出轴1或输出轴2位置的锥齿轮副)的回差减小3.4′，则两侧锥齿轮副(输出轴1与输出轴2位置的锥齿轮副)总的回差减小6.8′。因此，为保证差速机构低温不发生卡滞，室温(25 ℃)环境下其两侧锥齿轮副之间(即输出轴1与输出轴2之间)的传动回差应不小于6.8′。

差速机构装配过程中可通过调整垫片调整大锥齿轮在壳体上的安装位置(如图1所示)，以调整大小锥齿轮啮合侧隙，进而调整啮合传动回差。假设每侧大锥齿轮位置调整垫片厚度为x，小锥齿轮无调整垫片，此时ΔS1=x，ΔS2=0。由式(1)和式(8)～(10)可求得x厚调整垫片导致每侧锥齿轮副传动回差增大ε′(计算见式(11))，则两侧锥齿轮副回差增大2ε′。

(11)

2.2 锥齿轮传动回差估算正确性验证

为了验证回差估算数学模型的正确性，本节以差速机构工程样机为试验平台，通过在调整垫片位置安装不同厚度垫片改变4个锥齿轮之间的相对位置，以产生不同的传动回差，将该传动回差实测值与利用回差估算数学模型计算的理论值对比，从而验证回差估算数学模型的正确性。

差速机构装配过程中通过调整垫片厚度x控制传动回差，取调整垫片厚度x分别为0.00 mm，0.05 mm，0.10 mm，0.15 mm，差速机构左右两侧输出轴之间的传动回差实测值在第3.1节中的差速机构试验件上测试，同时利用式(11)对4种调整垫片条件下的理论传动回差增大量进行计算。4种调整垫片下差速机构两侧大锥齿轮输出轴之间传动回差实测值与理论值，如表3所示，变化趋势如图4所示。0.00 mm调整垫片传动回差实测值即为差速机构未安装调整垫片时的传动回差，该情况下由式(11)计算的回差增大量为0.00 mm，为便于数据比对，该情况下的理论回差值用测试回差均值代替。

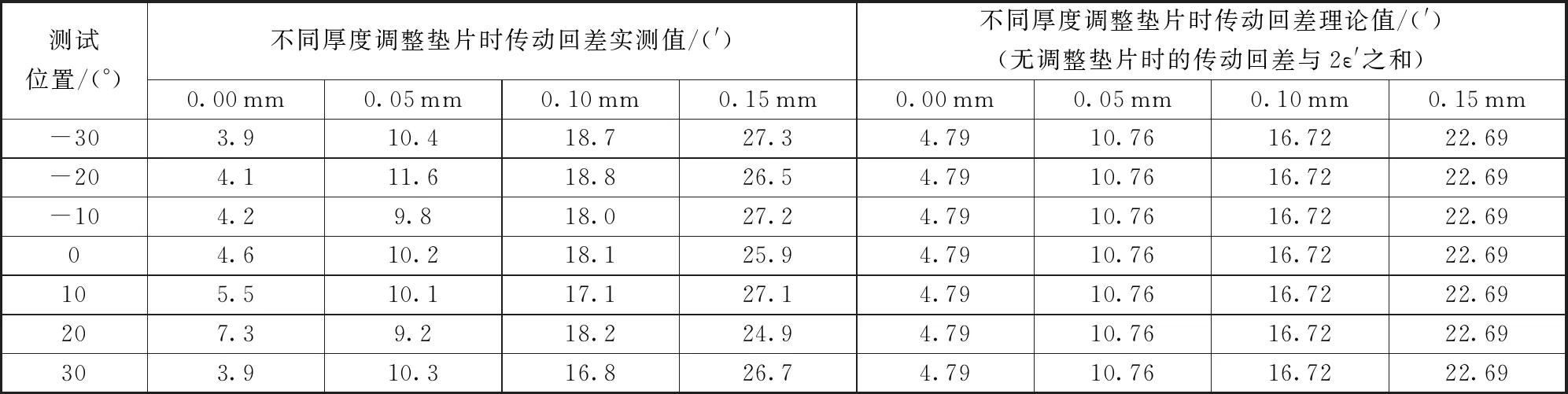
表3 不同调整垫片对应的差速机构传动回差

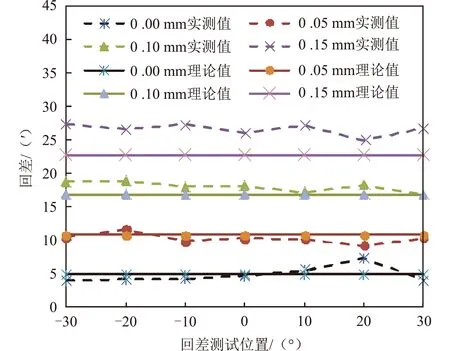
图4 不同调整垫片对应的差速机构传动回差变化

由表3和图4可以看出：调整垫片厚度分别为0.00 mm，0.05 mm，0.10 mm时，差速机构理论传动回差与实测传动回差均较为一致。当调整垫片厚度为0.15 mm时，差速机构理论传动回差略虽小于实测传动回差，但仍较为接近。造成实测传动回差大于理论传动回差的原因是：当调整垫片较厚时，锥齿轮实际啮合区域会向齿顶位置偏移，而理论计算回差时始终认为锥齿轮啮合位置在分度圆上。因此，本文提出的试验表明传动回差估算数学模型可对差速机构冷缩时传动回差变化量进行预测，可用于指导差速机构低温传动适应性设计。

3 试验验证

3.1 差速机构试验件

锥齿轮式差速机构低温传动适应性测试用试验件选用祝融号火星车差速机构工程样机。该样机设计时采用传动回差估算数学模型对传动回差进行控制，以保证差速机构低温传动无卡滞、高温车体俯仰小。差速机构样机传动回差控制用调整垫片厚度取为0.10 mm，保证差速机构从室温25 ℃降低到-65 ℃后，其传动回差即使减小6.8′也仍不小于10′，确保低温传动不卡滞。

差速机构工程样机核心部件如壳体、锥齿轮、输出轴等均采用轻量化设计，以大锥齿轮为例，其一方面切除了不参与啮合的齿，另一方面齿轮与齿轮轴采用不同材料。大小锥齿轮采用标准渐开线齿形，模数为2.5 mm，齿数分别为13和33，齿宽为14 mm。差速机构核心部件及强度分析如表4所示，强度分析载荷取为156 N·m(火星车车体最大设计弯矩)。差速机构工程样机实物如图5所示，其质量约为1.6 kg。

表4 差速机构核心部件强度分析

图5 差速机构工程样机

3.2 差速机构常温常压传动性能测试及结果

差速机构低温传动适应性测试前，首先进行常温常压性能测试以确认装配合理，主要包括空载传动回差、空载启动力矩、小负载俯仰空程等测试。测试结果如表5所示，常温常压下差速机构传动性能良好。

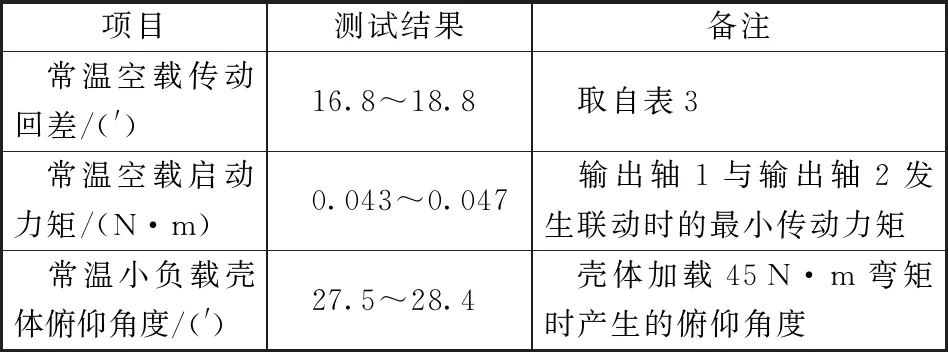
表5 差速机构样机常温传动性能

将差速机构样机与模拟车体进行联试(如图6所示)，其可承载整车俯仰弯矩、同时车体首尾俯仰晃动量等满足需求。

图6 差速机构与模拟火星车体联试

3.3 差速机构低温传动适应性测试及结果

低温传动适应性测试主要考核差速机构在低温环境下传动是否平稳、是否卡滞、低温启动力矩与常温启动力矩是否接近等。祝融号火星车差速机构设计时覆盖的存储温度范围为-130～+70 ℃，工作温度范围为-60～+55 ℃，本文对差速机构经历低温存储和低温循环2种工况后的低温传动适应性进行测试。

差速机构低温传动测试状态如图7所示，力矩传感器置于真空罐外侧，其可感知差速机构传动的平稳性、低温启动力矩、是否卡滞等，罐内的差速机构经磁流体密封装置与罐外的力矩传感器连接。试验工况1是将差速机构由室温降到-135 ℃低温中存储12 h后，将温度回升到-60 ℃并保温4 h，对差速机构空载和带负载条件下的传动性能进行测试；试验工况2是将差速机构由室温降到-65 ℃低温中停留4 h，对差速机构空载条件下的传动性能进行测试。2种工况下测试结果如表6所示，2种工况下差速机构低温均运转平稳无卡滞，156 N·m弯矩负载条件下差速机构低温启动力矩与常温启动力矩基本一致，证明该差速机构的锥齿轮间在低温环境中仍留有合理的传动间隙，传动回差控制合理；空载条件下差速机构低温启动力矩比常温启动力矩增大约5～10倍，这主要与磁流体密封装置运转力矩不稳定且受温度变化影响大有很大关系，空载条件下差速机构启动力矩湮灭在了磁流体密封装置运转力矩中。上述试验进一步表明本文提出的传动回差估算数学模型可指导锥齿轮式差速机构低温传动适应性设计以及工程样机研制。

图7 差速机构低温传动测试

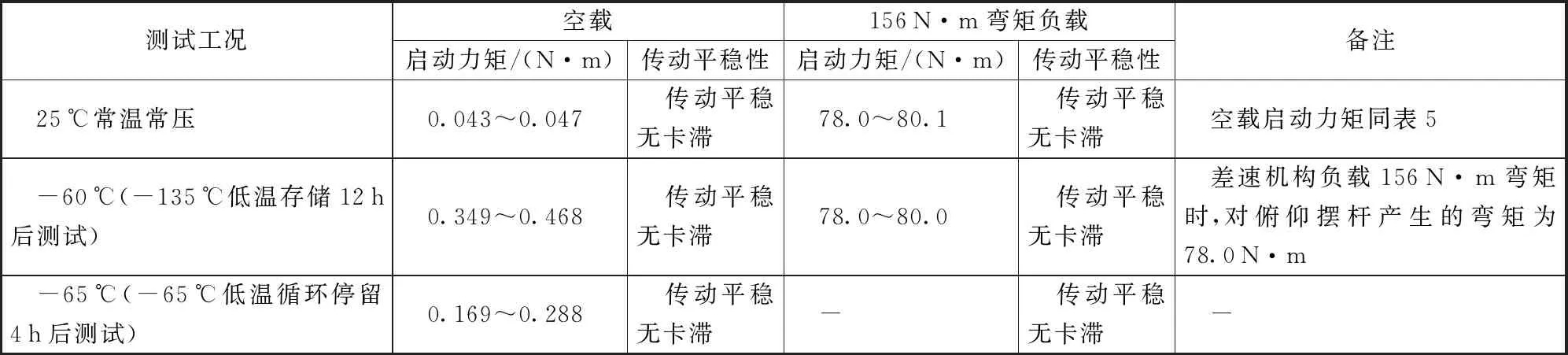
表6 差速机构低温传动性能测试结果

4 结束语

锥齿轮式差速机构传动回差估算数学模型综合考虑了温度变化、组成材料、零部件基本尺寸等设计参数，可预测温度变化对差速机构传动回差的影响，其计算的差速机构传动回差理论值与实测值基本一致，该模型在指导宽温域工作的锥齿轮式差速机构设计中具有重要意义。该传动回差估算数学模型已应用于祝融号火星车差速机构设计，为确保差速机构低温传动不卡滞，经模型分析计算出祝融号火星车差速机构常温传动回差应不大于6.8′，结合设计实现并预留一定裕度选择传动回差控制用调整垫片厚度为0.10 mm，控制差速机构常温传动回差为16.8′～18.8′。在经历-135 ℃低温存储或-65 ℃低温循环后、在空载或负载156 N·m弯矩条件下，该差速机构在-60 ℃和-65 ℃时的启动力矩、传动平稳性与常温时基本一致，低温传动适应性良好。