虹吸排水自补偿降雨量测量装置*

王先贺，陈华民，童仁园，葛仁望，陈向阳，李 青*

(1.中国计量大学灾害监测技术与仪器国家地方联合工程实验室，浙江 杭州310018；2.金华市地质环境监测站，浙江 金华321000)

我国是一个多山的国家，是地质灾害频发的国家之一。 由于全球气候异常变化，我国局部地区短时间内出现暴雨、特大暴雨的情况日渐增多，这使得发生滑坡和泥石流等地质灾害的隐患也在不断增加[1]。 短时间内持续性的强降雨是引发的滑坡和泥石流等地质灾害的关键因素，因此，如何实时、准确地获取降雨数据，及时采取防范措施，降低不必要的损失，对于地质灾害的预警工作显得尤为重要。

雨量计是气象及社会各相关部门普遍应用的测量降雨的仪器，是指能记录和显示降雨量的观测仪器。 目前国内应用较多的雨量计有翻斗式、虹吸式、称重式、压电式等多种类型[2-3]。 但每种类型的雨量计在精度或操作上都有一定的局限性。 翻斗式雨量计受降雨强度大小的限制，雨越大，测量误差越大[4]；虹吸式雨量计虹吸过程会漏记降雨量，而且必须定时到现场去更换记录纸，操作繁琐[5-6]；称重式雨量计不能自动排水或排水不及时，造成降雨测量数据不准确[7]；压电式雨量计受环境影响大，风、灰尘等易引起雨量板振动频率变化，导致数据误差变大[8-9]。 国外上世纪50年代就开始了降雨自动计量的研究，起步较早，目前已经实现了降雨的连续、非接触自动测量，国外比较成熟的产品有:芬兰VAISALA 公司生产的PWD22 天气现象传感器[10]，德国OTT 公司的Parsivel 激光降水粒子谱测量系统[11]，美国Borrmann 和Jaenicke 研制的全息液滴和气溶胶系统。 以上测量系统也有测量不准确，易受环境影响等缺点[12]。 国内对于雨量计的研制工作起步较晚，存在一定的差距，因此，研究一款可以精确测量降雨量的装置意义重大。

针对以上问题，在传统虹吸式雨量计的基础上进行了改进，设计了一种虹吸排水自补偿降雨量测量装置。 提出了该装置的系统结构及原理技术，设计了硬件电路，实现了自动化监测，建立了一套完整的降雨监测系统。 针对虹吸排水带来的计量误差问题，建立了一种高精度虹吸补偿数学模型，有效地提高了测量精度和灵敏度，在降雨监测领域具有很好的应用前景。

1 系统结构及测量原理

为了解决传统虹吸式雨量计虹吸时产生计量误差的问题，实现对降雨的高精度监测，设计了虹吸排水自补偿降雨量测量装置，结构示意图及实物图如图1、图2 所示。 其工作流程可表述如下，当有降雨发生时，降雨顺着承水漏斗流入盛水器，盛水器中的水位便随之上升。 当盛水器中的水位高度达到A点时，盛水器中的雨水便会由于虹吸作用，顺着虹吸管自动排出到装置外，直到盛水器中的水位降到O点，虹吸排水才算结束。 我们将盛水器中的水位从O点开始，上升到A点后，发生虹吸排水再回落到O点的过程，称为一次降雨虹吸过程。 当发生虹吸排水时，测量装置处于一边接水一边放水的状态，那么虹吸排水的这段时间里的降雨也会被随之排走而漏记，所以需要对虹吸过程中漏记的降雨进行补偿，本文提供了一种高精度虹吸补偿数学模型对虹吸排水过程造成的计量误差进行补偿。 虹吸补偿算法将在下面章节详细介绍。

图1 装置结构示意图

图2 装置内部结构实物图

本文的测量原理如下，当降雨发生时，测量装置收集降雨，位于盛水器底部的称重传感器的输出电压会随雨水重量的不同而产生相应变化。 然后将称重传感器输出的电信号传送给数据采集系统，由数据采集系统中的内部电路完成相应的差分放大、模数转换、滤波、数据处理、虹吸补偿等处理工作，得到精准的降雨重量，再把降雨重量转换成降雨量，通过电路搭载的4G 物联网模块，将降雨数据上传到阿里云平台，实现远程监测。

2 测量系统的研究与设计

2.1 虹吸管的设计

虹吸管作为雨量计的排水部件，性能的优劣直接影响到整套设备的设计要求，因此选取合适的虹吸管非常重要。 虹吸管的工作原理是利用虹吸现象引起排水的自然过程，无需消耗能量，因此非常符合系统低功耗的设计要求。 发生虹吸排水时，当水面升至弯曲段时，由于水的重力作用，下浸润边超前上浸润边，当水达到虹吸管顶时，下浸润边可能产生滴水，带来测量误差。 通过多次实验验证后，最终选用玻璃弯管弧度为28°，管内径为4 mm，厚度为1.5 mm 的虹吸管，虹吸管结构示意图如图3 所示。 当临近虹吸时，该虹吸管不会发生滴水现象；当雨水达到虹吸高度时，也不会出现虹吸无法发生的现象。 根据国家标准《GB/T 21978.3-2008 降雨量观测仪器》，连续降雨强度范围为0.01 mm/min～4.00 mm/min，通过查阅资料了解到，国内最大降雨速度的记录发生在1971年7月1 日，山西太原地区古交市梅洞沟，5 min 降雨量达53.1 mm，平均每分钟的降雨量为10.62 mm。 该虹吸管的最大排水速度18.3 mm/min，不会发生阻流现象，满足设计要求。

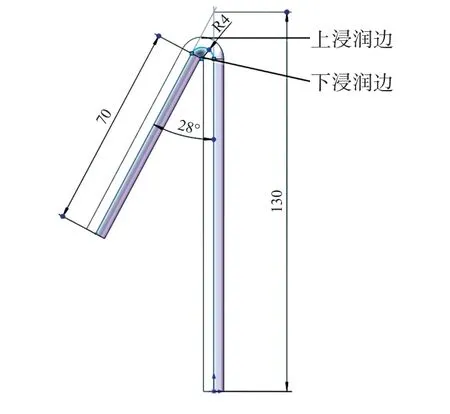
图3 虹吸管结构示意图

2.2 应变式称重传感器工作原理

传感模块采用的是电阻应变式称重传感器，其工作原理是弹性体在外力作用下产生弹性变形，使粘贴在它表面的电阻应变片也随同产生变形；电阻应变片变形后，它的阻值将发生变化，再经相应的测量电路把这一电阻变化转换为电信号输出。 该类型传感器精度高、频响特性好、结构简单、易实现小型化、耐劳时间长、能在恶劣条件下工作，符合应用条件。 电阻应变式称重传感器机械结构和内部电路图如图4 所示。

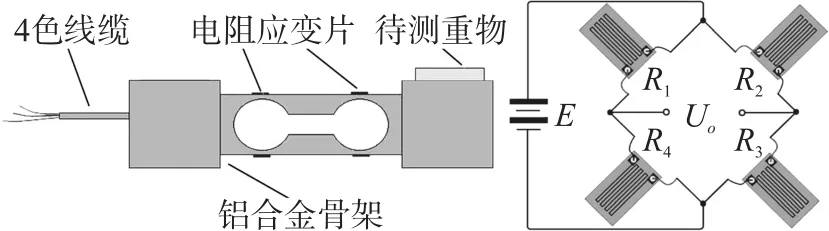
图4 称重传感器机械结构和内部电路图

该传感器的工作原理主要是利用了应变电阻的压阻效应和惠斯通电桥的平衡原理，惠斯通电桥的输出电压为:

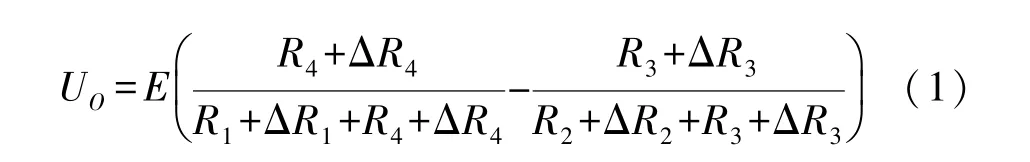
式中:E为激励电压，R1～R4为应变电阻的阻值，ΔR为应变电阻因形变产生的变化量。 有R1=R2=R3=R4=R，此时惠斯通电桥的输出电压为:

惠斯通电桥能感应微小的电阻变化，使电桥产生一个与压力成正比的高度线性、与激励电压也成正比的电压信号[13]。

2.3 称重传感器的电路设计

称重传感器电路决定着测量系统的工作效果，称重传感器的硬件电路主要包括:信号采集电路、放大滤波电路、模数转换电路、无线传输电路、测温电路、供电电源电路以及微控制器，具体设计框图如图5所示。

图5 硬件电路设计示意图

称重传感器会将降雨重量转化为微弱电压信号输出，经过差分放大电路和滤波电路完成信号放大和噪声滤除，数模转换电路将采集到的电信号转化为数字信号以SPI 串行通信的方式传输至微控制器，微控制器对采集到的数字信号进行了软件滤波，本设计使用了“滑动平均值滤波法”，并且在“滑动平均值滤波法”的基础上先得到一定数据宽度的滑动窗口数据，然后进行“中值滤波”，最后求平均值，从而在一定程度上减小干扰信号的影响。

接下来将滤波后的数字量和砝码进行标定，得到砝码重量与数字量的关系。 本设计以0.2 g 为一个单位进行标定，从0 g 至满量程1 kg 依次增大砝码的重量，并进行多次重复测量，记录砝码的重量和数据采集系统得到的数字量，并根据最小二乘法原理，对测量数据进行曲线拟合，其关系曲线如图6所示，横坐标为数据采集系统得到的数字量，纵坐标为砝码重量。

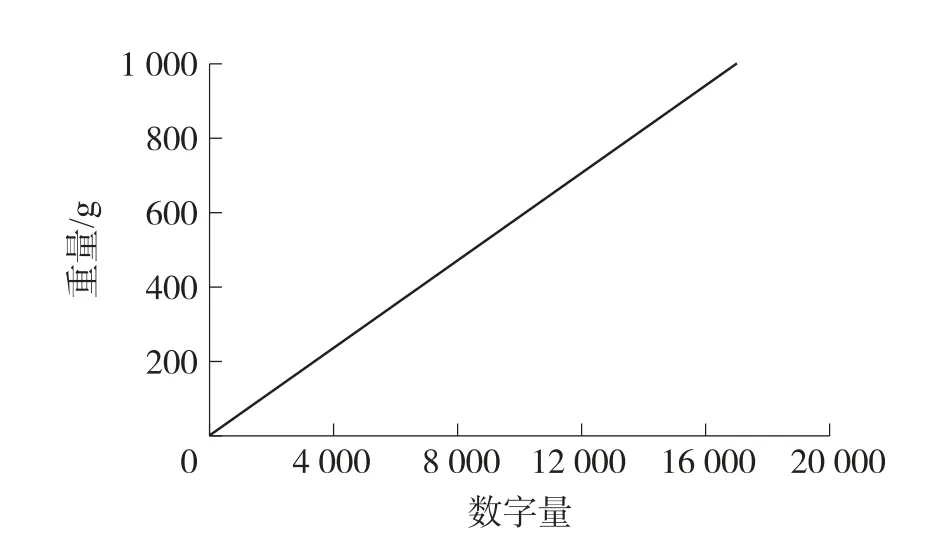
图6 称重标定曲线图

其线性表达式为:

其线性拟合曲线线性相关系数为0.999975，非常接近于1，说明数字量与砝码重量具有良好的线性关系。 标定完成后，制作完成的电子秤量程为1 kg，最小分度值为0.5 g，精度为1/2000。 电子秤实物图如图7 所示。 通过制作完成的电子秤测量降雨重量，微控制器进行数据处理和虹吸补偿，得到降雨数据，并通过物联网模块将降雨数据上传到阿里云平台实现远程监测。

图7 电子秤实物图

根据国家标准《GB/T 21978.3-2008 降雨量观测仪器》要求:虹吸式雨量计集雨桶直径为200 mm，分辨率要达到0.1 mm。 该电子秤的分辨率为0.5 g，已知水的密度ρ 为0.001 g/mm3，设计完成的雨量计集雨桶直径为200 mm，经计算，该雨量计的分辨率可达0.02 mm，符合设计要求。

考虑到本装置需要长期工作在野外进行降雨量的监测，实际的工况环境难以实现有线连接，因此要想保证装置能够长期稳定工作，装置所需能量的外部获取以及低功耗设计是非常重要的环节。 鉴于该装置放置在野外环境中工作，太阳能可作为一种稳定可靠的能量来源，所以本设计采用太阳能电池板和蓄电池作为装置的电源。 考虑到功耗问题，本装置的硬件电路设计均采用单电源供电，降低了功耗，简化了电路的设计结构。 另外，降雨过程是一个阶段性非持续的过程，因此对降雨的监测频率不需要太高，一个小时或者几个小时监测一次即可。 为了进一步降低功耗，设计了休眠/唤醒模式，通过STM32 单片机进行控制，使得装置可以根据实际需求工作在休眠和唤醒模式下。 如果没有发生降雨，系统便会工作在休眠状态，由于远程传输模块功耗相对较大，在休眠模式下，单片机会切断4G 物联网模块的供电网络，仅保留STM32 单片机、称重传感器、仪表运放AD8422 和模数转换芯片AD7606 的供电，休眠模式下，测量装置不会进行监测，这样会大大降低功耗。 当数据采集系统检测到降雨发生时，单片机控制系统会打开4G 物联网模块的供电电源，装置会自动对降雨进行监测。 以上工作状态都是由单片机控制系统自动完成的，经过试验测试，在太阳能作为直接能量来源的条件下，配合蓄电池在夜晚或者阴天的情况下提供电源，本装置能够实现长期稳定工作。

2.4 系统软件设计

系统软件设计流程如图8 所示。

图8 系统软件设计流程图

系统上电后，初始化各个模块，全部初始化完毕后就进入待机状态，不停地检测是否有数据传输过来。 当系统检测到有降雨发生时，便唤醒系统，处理数据，并把降雨数据发送至云端。 监测系统可以定时发送降雨数据，本设计每隔1 h 发送一次数据，如果前1 h 的降雨超过7 mm，监测端自动发出大雨报警。 如果监测系统检测到没有降雨或降雨停止，系统便进入待机休眠状态。

3 虹吸补偿算法数学模型

当发生降雨时，盛水器内的降雨重量逐渐增大，当盛水器内的水位高度达到虹吸点高度时(此时在虹吸点测得的降雨重量为mN)，由于虹吸作用，盛水器内的雨水便会通过虹吸管排出，盛水器内的降雨重量随之减小，一次降雨虹吸过程中盛水器内的降雨重量变化曲线如图9(a)所示。 由于虹吸排水的速度远远大于降雨的速度，最终盛水器内的雨水还是会被排出盛水器，只是有降雨时发生虹吸排水的时间要比没有降雨时的虹吸排水的时间要长一些[14]。

在发生虹吸排水的过程中，盛水器处在一边接水一边放水的状态，那么就会致使Δt这段时间的降雨会被随之排走而漏记，这里把漏记的降雨重量记为ΔmN，一次降雨虹吸过程中漏记的降雨重量ΔmN分析图如图9 所示。 那么如何找到一种补偿算法，得到一次虹吸排水过程中漏记的降雨重量ΔmN，成为提高测量精度的关键所在。

根据上述分析，本文提出了一种在虹吸发生时的测量补偿方法，以消除误差[15]。 首先分析一种理想的情况，假设在虹吸过程降雨速度和虹吸排水的速度都是匀速的，则虹吸排水曲线就是一条固定斜率的曲线，图9(a)是实际降雨过程中盛水器中的降雨重量变化曲线图。 图9(b)表示无降雨时虹吸发生时盛水器内降雨重量变化曲线图，从虹吸的机理可知，图9(b)降雨重量减小过程t1≤t≤t′2的曲线是盛水器和虹吸管制成后的固有曲线，不会随降雨量的变化而变化。 将有降雨发生时的虹吸过程(即t1≤t≤t2)盛水器内的降雨重量变化曲线(即图9(a)的A-B 线段)减去无降雨发生虹吸时盛水器内的降雨重量变化线段和该线段的延长线段(图9(b)中t1≤t≤t′2的实线和t′2≤t≤t2的点划线)，即可得到在t1≤t≤t2时间内实际降雨量对应的盛水器降雨重量变化曲线，如图9(c)虹吸过程漏记的降雨重量曲线图所示，从而得出一次降雨虹吸过程中漏记的降雨重量ΔmN。

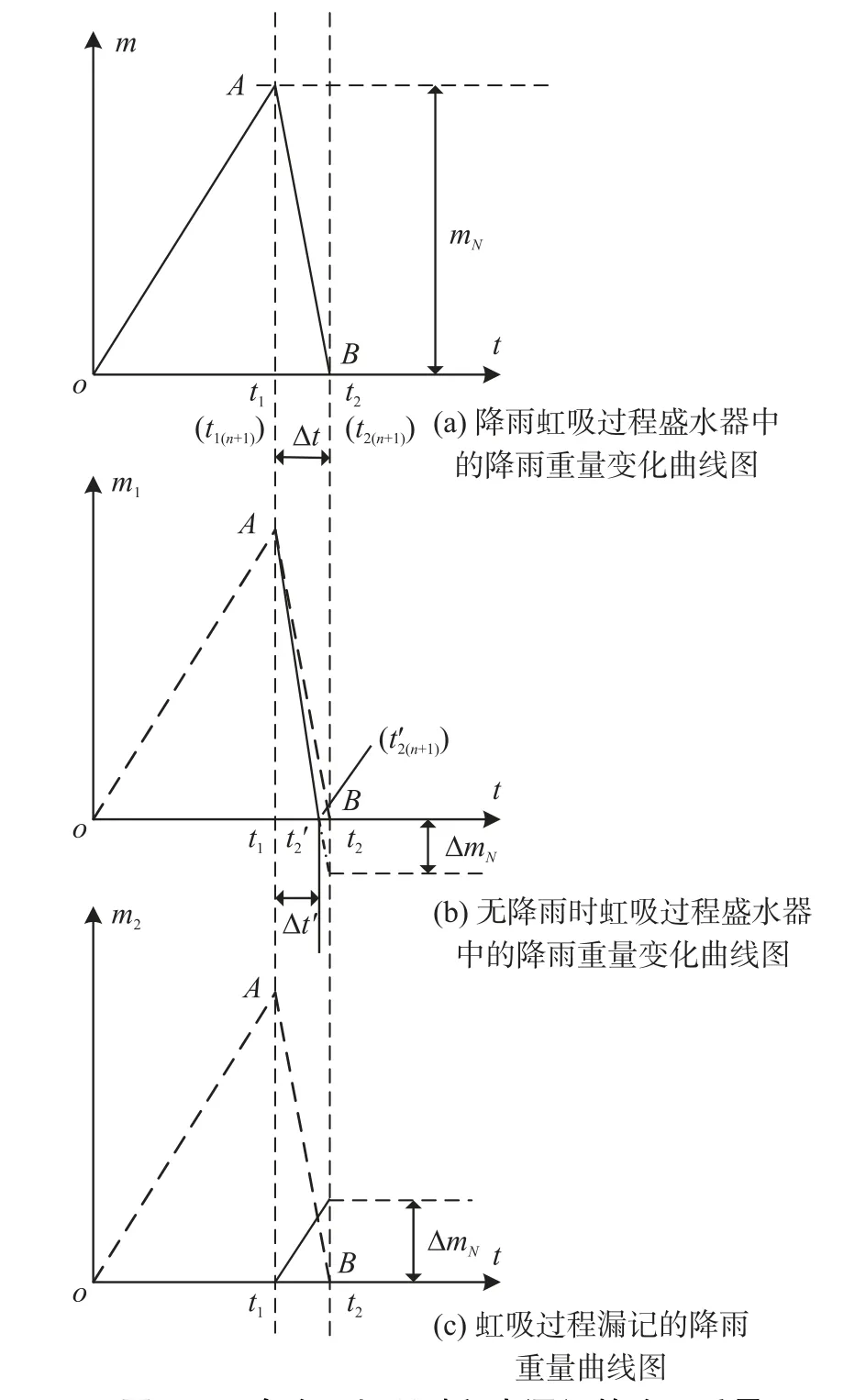
图9 一次降雨虹吸过程中漏记的降雨重量ΔmN 分析图

图9 中m(t)是降雨过程实际的盛水器内降雨重量变化的函数，m1(t)是无降雨发生虹吸时盛水器重量变化的直线和延长段直线的函数，m2(t)是测量过程中t1≤t≤t2时间内虹吸发生时的漏记的降雨重量变化的函数。 单次测量(其中0≤t≤t2)带补偿的测量函数关系:

式中:m(t)是由图2 的测量装置实际测出的；m1(t)是在虹吸管和盛水器的结构都定下后，专门标定实验测出其实线部分，再根据实线斜率延长，延长的长度由t2时刻决定，t2则是由降雨速率的大小决定，降雨速率越大则t2越大，降雨速率越小则t2越小，每一个单次测量循环的时间长度0≤t≤t2是不等的；mN是m(t)的最大值，即虹吸点的降雨重量，其大小也是由虹吸管和盛水器的结构决定。 由于实际降雨是变化的，m(t)的实际曲线不一定是直线，m2(t)也不一定是m(t)的O-A线段的平移。 根据上式，任何瞬时的降雨量测量表达式为:

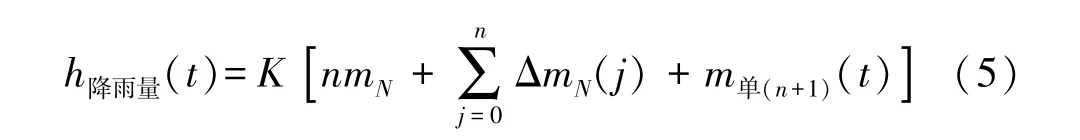
式中:ΔmN(j)是由第j＋1 次发生虹吸现象时(j∈Z)，在t1≤t≤t2时间内降雨重量的值，即如图9(c)所示的ΔmN，由于降雨的速率不是恒定量，一般各ΔmN(j)不等，即:ΔmN(j-1)≠ΔmN(j)≠ΔmN(j＋1)，且j＜0 时ΔmN(j)= 0；n表示已有n次虹吸完成，n∈Z；K是盛水器内的降雨重量转换成降雨量的比例系数；m单(n＋1)(t)是第n＋1 次的m单(t)，参考式(4)，得到m单(n＋1)(t)的表达式为:

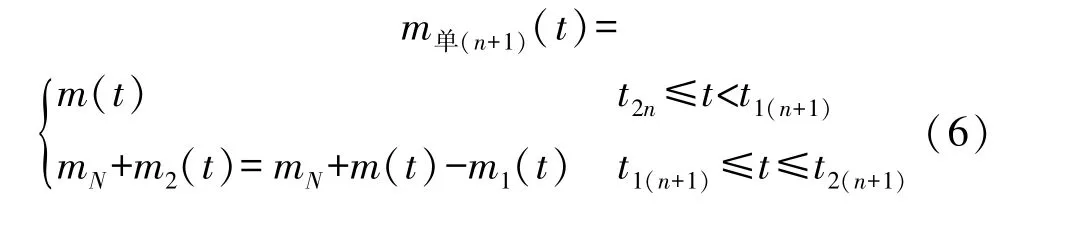
式(6)表述的是降雨过程中任何一次盛水器内降雨重量增加和虹吸排水的循环，当n=0 时表达是第一次盛水器内降雨重量增加和虹吸排水的过程；t′2(n＋1)≤t≤t2(n＋1)是固有的虹吸排水直线的延长段，t2(n＋1)可通过图9(a)到达最低点的时刻确定，这在测量装置的MCU 可用相应的判断程序实现，得到t2(n＋1)后，由MCU 的程序作虹吸排水直线的延长段，m1(t)在t1(n＋1)≤t≤t2(n＋1)内完全确定。 将式(6)的结果代入式(5)，则可得出带补偿关系的降雨量测量值h降雨量(t)。

4 实验数据处理与分析

4.1 有无降雨虹吸过程模拟实验

对上述提出的虹吸补偿算法模型进行试验验证，首先进行降雨模拟实验， 将雨速控制在0.9408 mm/min，根据实际降雨过程和虹吸过程得到的降雨重量数据，绘制降雨模拟曲线。 一次降雨虹吸过程盛水器内的降雨重量变化曲线如图10 所示，实际有降雨过程虹吸现象产生时的起始重量为mN；虹吸过程持续时间为t1～t2。

图10 一次降雨虹吸过程盛水器内的降雨重量变化曲线图

要想对虹吸过程中漏记的降雨量进行补偿，首先要得到没有降雨时虹吸过程曲线和有降雨时虹吸过程曲线的实验数据，如图11 所示，t′2为无降雨虹吸排水过程的时间长度，t2为有降雨虹吸排水过程的时间长度。

图11 有无降雨虹吸过程降雨重量变化对比曲线图

从虹吸补偿算法的理论分析可知，无降雨时虹吸过程是一条固有曲线，是由虹吸装置本身决定的。事实上，在实验过程中由于虹吸排水过程可能发生提前虹吸，会导致虹吸点的重量并不完全相同，相应的无降雨时虹吸过程的曲线也就不是唯一的。 为了解决这一问题，就进行了多次无降雨时的虹吸排水实验，绘制出多条虹吸排水过程重量变化曲线。 然后将无降雨时虹吸过程中的虹吸点重量划分了5 个不同的区间，根据不同的虹吸点重量区间，挑选出了5 条无降雨时的虹吸过程曲线，有针对性地对有降雨时虹吸过程中不同的虹吸点重量区间进行虹吸补偿。 无降雨时虹吸过程的曲线在某一虹吸点重量区间是唯一确定的。

根据上述分析，虹吸点的重量并不完全相同，降雨总重量的计算方法是将每次虹吸点重量和每次虹吸过程漏记的降雨重量进行叠加，并考虑降雨结束时没有达到虹吸点的降雨重量。 实际降雨过程任何瞬时的降雨量测量表达式为:

式中:mN(j)是由第j＋1 次发生虹吸现象时虹吸点的降雨重量，j∈Z，一般各mN(j)不等，即:mN(j-1)≠mN(j)≠mN(j＋1)，且j＜0 时mN(j)= 0。

4.2 虹吸补偿算法应用

由于实际得到的无降雨时虹吸过程曲线和有降雨时虹吸过程曲线是非线性的，而图9 的虹吸补偿算法的理论分析是建立在虹吸过程曲线是线性的基础上，那么现在需要将虹吸补偿算法推广到单调非线性的实际虹吸过程。

首先需要对实际得到的有无降雨时虹吸过程的曲线进行分析，有降雨时虹吸过程盛水器内降雨重量变化随雨速的大小而不同，可以根据实际降雨数据通过程序算法进行处理。 有降雨时虹吸过程的时间长度为t2，t2可以通过降雨过程降雨重量达到最低点时得到，通过最小二乘法对无降雨虹吸过程的曲线进行多项式拟合，得到L1(t)，将L1(t)按照自身的函数关系延长至t2，得到带补偿关系的虹吸过程降雨重量变化曲线，令其为L′1(t)。 此虹吸补偿方法记为算法A，如图12 所示。

图12 算法A 带补偿关系的虹吸过程降雨重量变化曲线图

将L(t)和L′1(t)两者相减的结果便是一次虹吸过程漏记的降雨重量变化曲线L2(t)，以上算法可以通过软件编程实现。 通过算法A 得到的虹吸过程漏记的降雨重量曲线如图13 所示。

图13 算法A 求得虹吸过程漏记的降雨重量曲线图

为了提高测量精度，找到最优的补偿算法。 经分析，由于实际的虹吸过程是一条曲线，而虹吸补偿算法的理论分析是建立在虹吸过程是一条直线的基础上。 因此，提出了一种新的数据处理算法对无降雨时虹吸过程的曲线L1(t)进行处理，首先找到无降雨时虹吸结束时间t′2，过点t′2并做其切线延长至t2，得到带补偿关系的虹吸过程降雨重量变化曲线，令其为，此虹吸补偿方法记为算法B，如图14 所示。

图14 算法B 带补偿关系的虹吸过程降雨重量变化曲线图

将L(t)和L″1(t)两者相减的结果便得到算法B一次虹吸过程漏记的降雨重量变化曲线L′2(t)，以上算法可以通过软件编程实现。 通过算法B 得到的虹吸过程漏记的降雨重量曲线如图15 所示。

图15 算法B 求得虹吸过程漏记的降雨重量曲线图

4.3 实验结果分析

利用降雨模拟试验场地模拟实际降雨的过程，调节水阀使得模拟降雨速度在0.1 mm/min ～1.0 mm/min的范围内，通过实验测得各个降雨速度下降雨虹吸过程的数据。 然后，将这些数据利用虹吸补偿算法A、B 求出虹吸过程中漏记的降雨重量ΔmN，通过MCU 程序计算得出一次降雨虹吸过程中的降雨量，并与实际的降雨虹吸过程中的降雨量进行对比，比较两种算法之间哪个误差更小。

实验选取了大雨、暴雨、特大暴雨三个降雨等级的雨速进行降雨模拟实验，将降雨速度设定在0.157 mm/min、 0. 314 mm/min、 0. 470 mm/min、0.627 mm/min、0.862 mm/min、0.941 mm/min，对这6 组实验样本数据采用虹吸补偿算法A、B 后，求得在一次降雨虹吸过程中(包括水位上升和虹吸排水过程)的降雨量，降雨量的误差分析如表1 所示。

表1 一次降雨虹吸过程中降雨量的误差分析

从实验结果可知，在一次降雨虹吸过程中，不作虹吸补偿算法的降雨量测量误差范围为2.682%～8.147%，经过虹吸补偿算法A、B 补偿后降雨量测量误差明显减小，其中算法A 的最大测量误差为2.127%，算法B 的最大测量误差为0.704%。 通过对虹吸补偿算法A、B 对比可知，算法B 的补偿效果较好，其测量误差范围在1%以内。 根据以上分析可得，虹吸补偿算法有效地消除了降雨随虹吸排水造成的计量误差，提高了降雨量的测量精度。

5 结论

为了解决传统虹吸式雨量计虹吸时产生的计量误差，提高降雨量的测量精度，实现降雨自动化监测，本文基于称重传感器研制了一种降雨量测量装置，并融合工业物联网技术开发了一套精密在线监测系统。 首先选择内部结构为一个惠斯通电桥的电阻应变式称重传感器，设计出弱小信号差分放大电路及基于单片机的数据采集处理系统，建立了虹吸补偿算法数学模型，通过对降雨重量信号的实时采集及模型计算，获取降雨量数据。 结果表明:将虹吸补偿算法数学模型应用于降雨量测量，有效地消除了降雨随虹吸排水造成的计量误差，降雨测量误差在1%以内，比传统虹吸式雨量计的测量精度更高。该装置具有供电方便、通信稳定、测量精度高等优势，在降雨量监测领域有极大的使用价值。