基于优化模糊加权核极限学习机的下肢运动识别方法*

赵 翔涂 娟*黄紫娟

(1.福州大学，电气工程与自动化学院，福建 福州350108；2.福建省医疗器械与医药技术重点实验室，福建 福州350108)

表面肌电信号(Surface Electromyography，sEMG)是一种易受实验环境影响的微弱生物电信号[1]，是由运动时肌肉兴奋所产生的动作电位序列在皮肤叠加而成，它一般比肢体运动超前30 ms ～150 ms[2]，易获取，主要依赖于驱动运动的肌肉，并不依赖于执行运动的肢体，广泛应用于人机交互技术[3]。 目前肌电信号特征提取方法有时域分析法、频域分析法和非线性分析法[4-7]。 下肢肌肉存在于皮肤深处，且彼此之间存在明显的重叠，与上肢肌肉相比，下肢肌肉表面肌电信号的分类更加困难[8]。采用多域特征融合进行动作分类，可以有效提高分类准确率。 文献[9]将时域特征和频域特征组合成多特征组合，用于步态识别，获得95%的平均识别率。 特征融合能够增加特征的多样性，但是增加了计算复杂度，并导致分类性能的下降。 文献[10]使用有监督降维方法局部Fisher 差别分析(Local Fisher Discriminant Analysis，LFDA)和无监督降维方法局部保持投影(Locality Preserving Projections，LPP)来处理冗余特征，提高了分类性能。

反向传播(Back Propagation，BP)神经网络通过实验数据正向传播、误差反向传播来训练神经网络，进行运动分类时会出现权值参数设置繁琐、且训练速度慢等缺点[11]。 黄广斌[12]提出了一种单隐层前馈神经网络算法，即极限学习机(Extreme Learning Machine，ELM)，学习速度比BP 神经网络要快，准确率也较高，但ELM 权重参数和隐含层神经元个数会对分类结果产生较大的影响。 核极限学习机(Kernel ELM，KELM)将正则化系数和核函数引入ELM，可以解决ELM 随机选择权重参数和隐含层神经元个数所造成的分类结果稳定性差的问题。 文献[13]采用量子粒子群算法(Quantum Particle Swam Optimization，QPSO)优化KELM 的正则化系数和核函数，提高了KELM 的泛化性能。 文献[14]使用模糊加权核极限学习机(KFWELM)来解决离散点和噪声样本对KELM 分类的影响，提高了分类性能，但处理数据的能力有待提高。

本文提出一种基于优化KFWELM 的下肢运动分类方法。 该方法分别使用LPP 和LFDA 对提取的EMG 多域特征进行降维处理，采用改进高斯量子离子群算法(Gaussian Quantum Particle Swarm Optimization，GQPSO)优化KFWELM 的正则化系数和核参数，提高KFWELM 处理特征的能力，最后进行自适应融合得到分类结果。 实验表明，该方法具有良好的分类精度，能够用来实现下肢运动的准确分类。

1 特征提取

为了更好地揭示下肢运动模式获取的EMG 信号的内在属性，提取其时域、频域、非线性特征，组成48 维多域特征。 如果将多域特征直接输入神经网络中，会出现特征冗余等问题，从而造成分类性能的下降，需要对特征值进行降维处理。 目前降维分为有监督降维和无监督降维，有监督降维主要考虑特征实现数据有效的分类，无监督降维主要考虑低维特征有效地表示高维特征。 有监督降维方法LFDA[10，15-16]通过选定一个较优的投影方向，将高维问题降低到一维问题，变换后的一维数据既可以聚集每一类的数据，又可以使不同类的数据尽可能分隔开。 因此在进行降维处理时，可以在实现最大区分类间可分性的同时保持类内局部特性。 无监督降维方法LPP 处理特征值时能够保持其局部性[10，17]。 本文结合这两种降维方式的优点，同时使用有监督LFDA 降维和无监督LPP 降维，最后进行自适应融合，以提高分类性能，尽可能减少原特征的信息损失，更全面地分析数据特征。

2 模糊加权核极限学习机的自适应融合算法

2.1 模糊加权核极限学习机(KFWELM)

ELM 是一种单隐含层前馈神经网络[12]，随机产生输入层权重和偏差，并使用广义逆矩阵求解出输出权值，测试数据利用训练好的输出权值实现分类或回归。 隐含层节点、输入权重和偏差对模型性能会产生极大的影响，对此引入核函数，构建KELM，对输入数据进行核映射，进而求出输出权值。 为了进一步消除离散点和噪声样本对KELM分类的影响，处理不平衡数据，采用模糊加权核极限学习机(KFWELM)。

给定N个任意样本组成的数据集(xj，tj)，其中tj=[tj1，…，tjm]T∈Rm，xj=[xj1，…，xjn]∈Rn，第j个输入样本xj是n×1 个特征向量，第j个输出样本tj是m×1 个编码后的目标输出向量，KFWELM 表示为[14]:

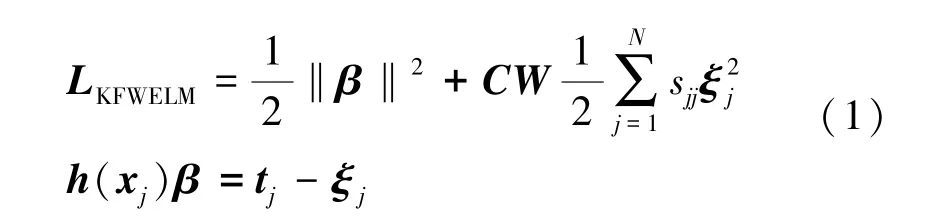
式中:W为权重矩阵，S为模糊隶属度，sjj为S的对角元素，h(·)为隐含层输出向量，C为正则化系数，tj为输出向量，xj为输入向量，β为输出权值，ξj为训练误差。

权重W表示如下:

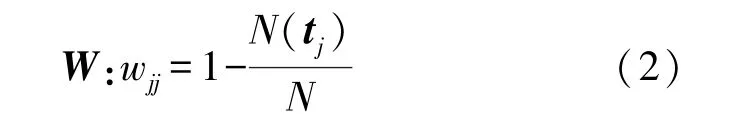
式中:W是对角矩阵，wjj为W的对角元素，N(tj)是tj类中的样本数，N是样本总数。

模糊隶属度S的计算:

①考虑训练样本和样本中心距离的模糊隶属度定义为:

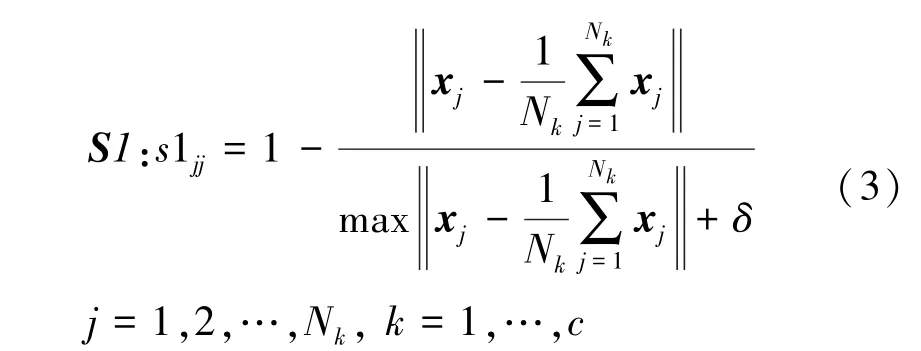
式中:xj是第j个输入样本，Nk是第k类输入样本数，c是类别数，δ是任意小的正数，S1为对角矩阵，s1jj为S1的对角元素，

从式(3)中可以看出，赋予噪声样本等最小的模糊隶属度，以减少对分类的影响。

②使用K近邻(K Nearest Neighbor，KNN)分类方法来度量训练集周围的关联性，第k类的样本xj周围的关联性定义为:

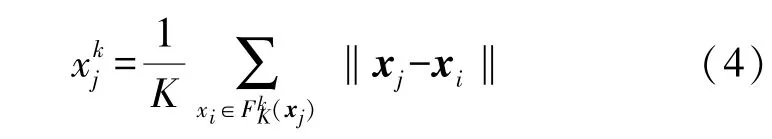
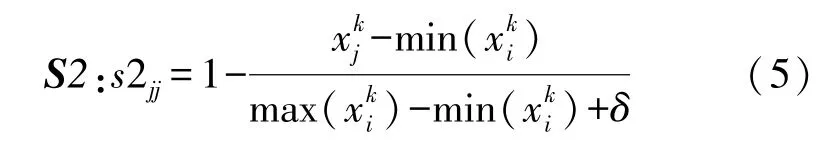
从(5)中可以看到离散值和噪声样本的关联性是稀疏的，因此离散值和噪声样本也将被赋予最小模糊隶属度。

将S1和S2相结合的模糊隶属度S定义为:

式中:S是对角矩阵，sjj是S的对角元素。

运用KKT[12，18]原理求解(1)，输出权值β定义为:

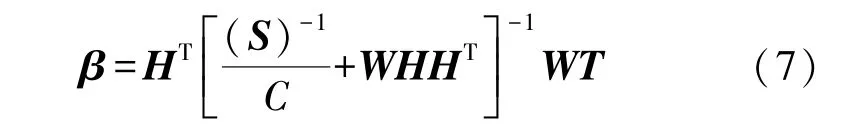
式中:H为隐含层输出矩阵，H= [h(x1)，…，h(xN)]T，W为权重矩阵，S为模糊隶属度，C为正则化系数，T为输出矩阵。

KFWELM 的输出函数矩阵为:

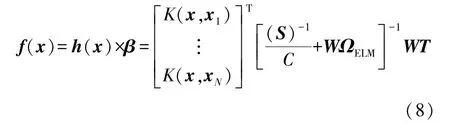
式中:ΩELM=HHT，h(xi)×h(xj)=K(xi，xj)=ΩELMi，j，小波核函数K(xi，xj)为:

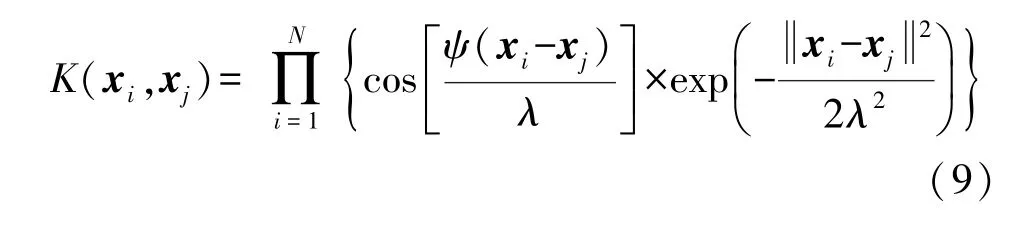
式中:ψ和λ为核参数，适当选择可提高算法性能。

2.2 改进高斯量子粒子群算法

KFWELM 的正则化系数和核参数需要人为设定，为提高KFWELM 的泛化性能和稳定性，使用优化算法对这两种参数进行优化。 GQPSO 在进行参数寻优时，采用高斯变异算子替代随机序列，可以防止其过早收敛，提高寻优的能力，但还是有陷入局部最优值的可能[19]。 为此提出一种扰动式的动态惯性权重来改进GQPSO，对KFWELM 的正则化系数(C)和核参数(γ和ψ)进行优化，并使用混沌映射产生初始化参数，提高算法的全局寻优能力。

GQPSO 的基本公式为:

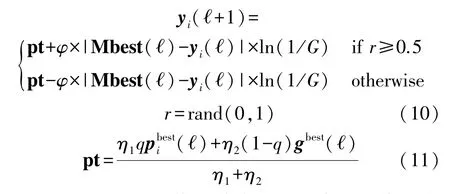
式中:利用具有零均值和单位方差的高斯概率分布的绝对值来产生随机数G和q，即为abs(N(0，1))，Mbest(ℓ)是个体最优值的平均值，φ为惯性权重，ℓ为当前迭代次数，yi(ℓ)为粒子当前位置，pbesti(ℓ)为当前粒子的最优位置，gbest(ℓ)为当前所有粒子的最优位置，η1和η2为学习因子。

使用混沌映射初始化粒子位置，可以提高粒子的整体性和多样性，取得比伪随机数更好的结果，本文使用Logistic 映射进行粒子种群初始化:

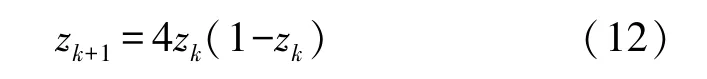
式中:zk是第k个混沌数，范围为0 到1 之间，z0∈rand(0，1)且z0∉(0，0.25，0.5，0.75，1)。

初始化粒子群位置(y(start))为:

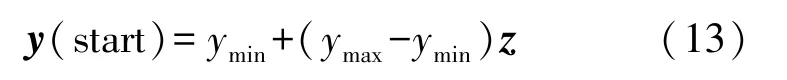
式中:ymax和ymin分别为粒子位置最大值和最小值。z为Logistic 映射后的初始矩阵，范围为0 到1之间。

为避免算法陷入局部最优，采用一种扰动式的动态惯性权重来更新粒子的位置，使得权重虽然整体呈减少趋势但是在一定范围内波动，提高算法全局搜索能力:

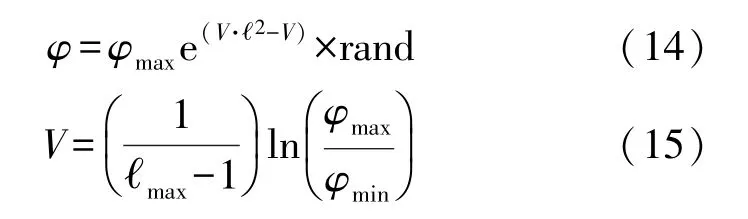
式中:φmax和φmin分别为惯性权重的最大值和最小值，ℓmax为最大迭代数。

改进GQPSO-KFWELM 基本步骤如下:

①改进GQPSO 的最大进化代数为ℓmax=400，粒子群种群规模为M=100，惯性权值的最大值φmax和最小值φmin分别取0.9 和0.4，学习因子分别为η1=1.49 和η2= 1.49，粒子位置设定为yi(ℓ)=[Ci(ℓ)γi(ℓ)ψi(ℓ)]T，粒子位置最大值和最小值分别为ymax=600 和ymin=0.01，并采用混沌序列进行粒子种群初始化。

②使用五折交叉验证产生训练集和验证集，将其平均分类准确值作为适应度。 将当前计算的适应度值与该粒子最优位置的适应度值进行比较，选择适应度值较大粒子的位置作为新的。 将当前计算的适应度值与所有粒子最优位置gbest(ℓ)的适应度值进行比较，选择适应度值较大粒子的位置作为新的gbest(ℓ)。

③根据式(10)和式(11)来更新每个粒子的位置。

④判断yi(ℓ)中的数据是否超出了范围，若yi(ℓ)中的数据大于ymax，取ymax，若yi(ℓ)中的数据小于ymin，取ymin。 对最大迭代次数进行检验，检查当前迭代次数大于等于ℓmax时，得到最优参数gbest=[Cbestγbestψbest]T，反之则令ℓ=ℓ＋1，继续执行步骤②～步骤④。

2.3 分类器融合

为防止单一降维造成信号特征的缺失，同时使用有监督LFDA 和无监督LPP 对特征进行降维，并在决策级对最终处理后的数据进行自适应融合。 根据参考文献[20]，首先将运用这两种降维方式组成的输出矩阵f(x)转换成概率输出矩阵，记为PI(x)

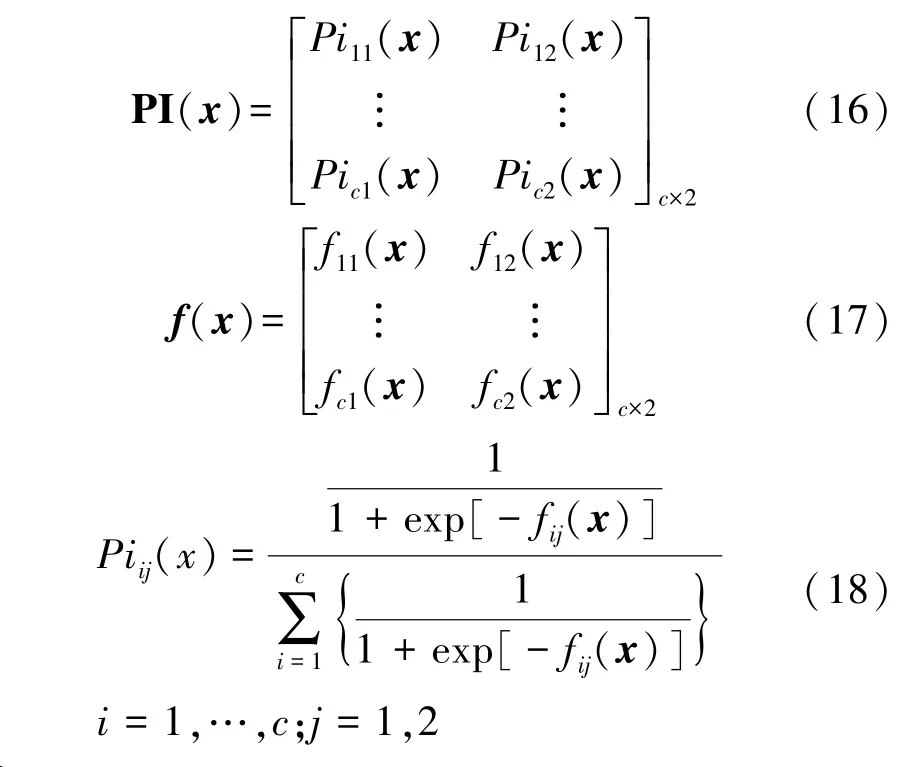
式中:c为类别数

融合权值计算方式为:

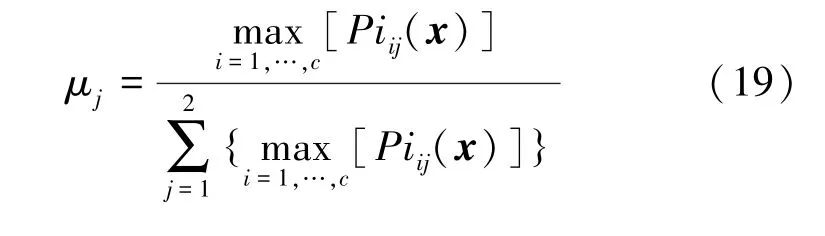
将每组分类器中的概率进行加权处理，加权结果最大标签作为融合结果的输出，即为:

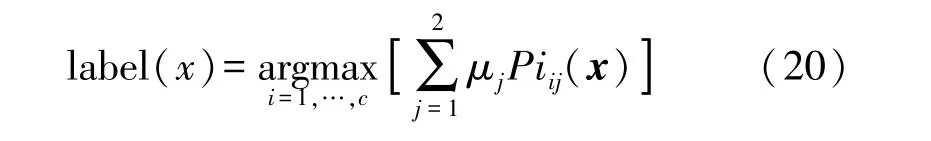
3 实验结果

3.1 数据描述

本文使用UCI 数据库(http:/ /archive.ics.uci.edu/ml/datasets/EMG＋dataset＋in＋Lower＋Limb)，该数据库提供了22 名18 岁以下的男性参与者下肢的4 通道EMG 数据和1 通道测角仪数据，参与者中11人健康，11 人有膝关节病变(6 人前交叉韧带损伤，4 人半月板损伤，1 人坐骨神经损伤)。 采集股内侧肌、半腱肌、股二头肌和股直肌的表面肌电信号，并将测角器保持在膝关节外侧。 分别记录坐着伸膝、站立屈膝、平地行走3 种三种运行方式的EMG 和膝关节角度。 最后把4 通道EMG 数据分成具有64 ms重叠的256 ms 窗口。

3.2 实验步骤

将预处理后的表面肌电信号提取时域、频域、非线性特征，组成48 维特征，采用本文方法进行下肢运动分类，其中正则化系数与核参数的范围为0.01～600，最后使用三折交叉验证算法分类的准确率，算法流程如图1 所示。

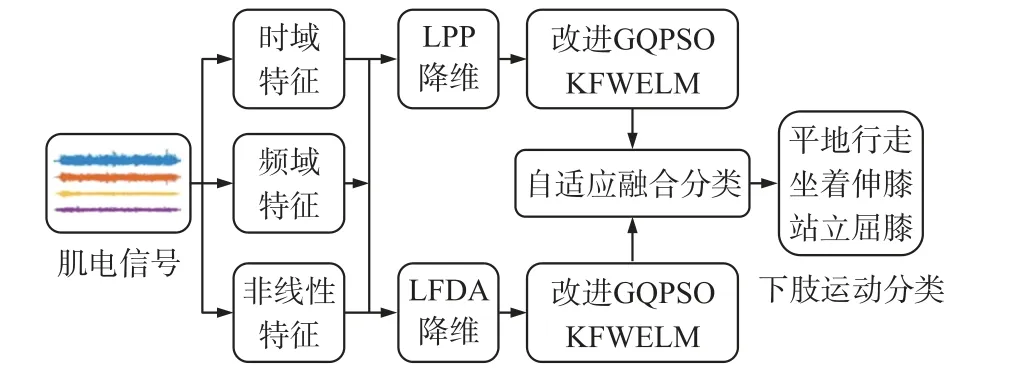
图1 算法流程图

3.3 实验结果与分析

使用BP、KNN、ELM、KELM、KFWELM、GQPSOKFWELM 和本文方法对UCI 数据库中的数据集进行下肢运动识别，健康人群和患病人群的算法分类性能如表1 所示。 将多域特征直接输入BP、KNN、ELM、KELM、KFWELM 和GQPSO-KFWELM 进行训练测试；本文方法使用LFDA 和LPP 对48 维特征降维处理。

从表1 看出，在对健康人群和患病人群进行坐着伸膝、站立屈膝、平地行走三种下肢运动识别中，相较于传统的分类算法，KFWELM 的分类准确性更高，说明构建权重和模糊隶属度可以提高KELM 处理特征值的能力，从而提高分类准确率。 本文提出使用GQPSO 优化KFWELM 的正则化系数和核参数，实验结果表明，对健康人群和患病人群的三种下肢运动识别率与KFWELM 相比较，分别提高了0.022、0.008、0.011 和0.011、0.014、0.009，采用GQPSO-KFWELM 方法可以有效解决随机选择KFWELM的正则化系数和核参数所带来的鲁棒性差、分类准确率降低等问题，提高了KFWELM 的泛化性能和分类准确率。 本文方法的运动识别准确率是最高的。 在GQPSO-KFWELM 的基础上采用有监督和无监督降维、决策级融合的分类方法，有效地解决了多域特征的冗余性会造成GQPSO-KFWELM 分类性能下降的问题。

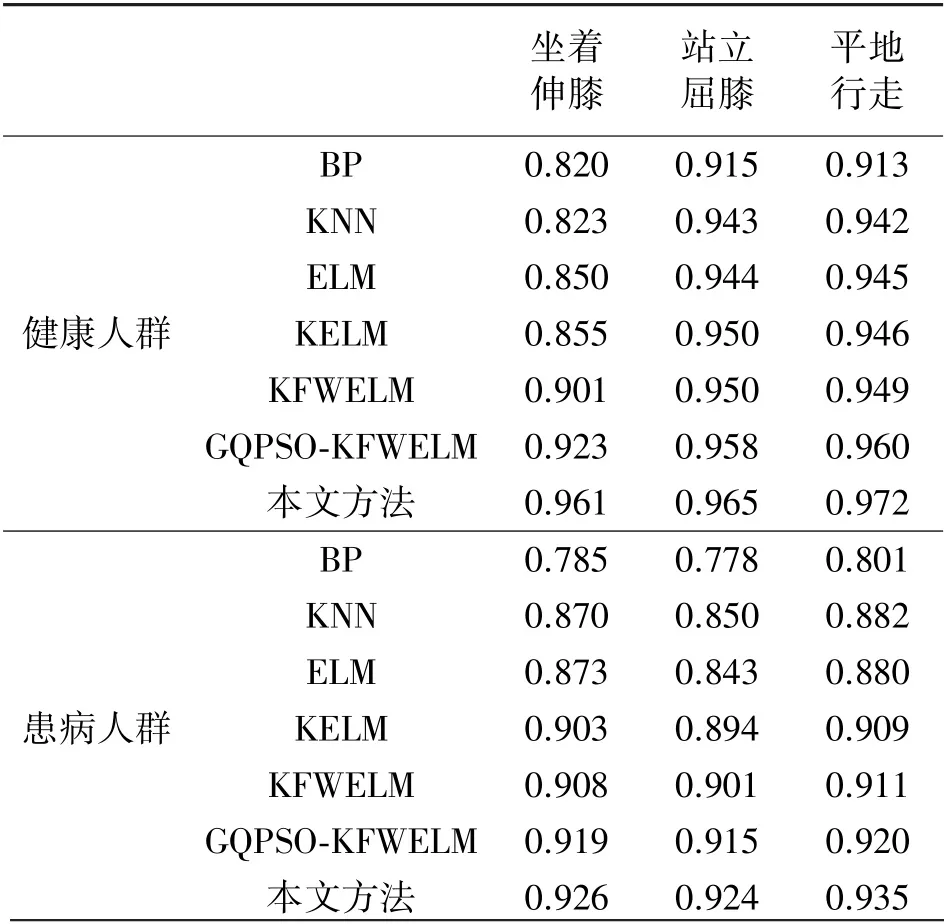
表1 本文方法与传统方法的分类准确率对比

表2 为本文方法与已发表且采用相同数据集验证的改进算法性能对比。 本文提出的改进算法可以有效提高坐着伸膝、站立屈膝、平地行走三种下肢运动识别准确率。

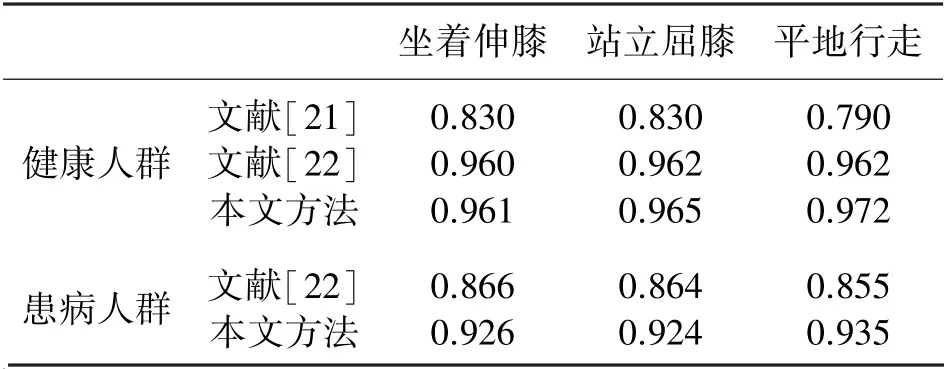
表2 本文方法与已发表论文方法的分类准确率对比

4 结论

针对不同情况下获取的表面肌电信号存在差异性等问题，本文提出了一种优化KFWELM 的分类算法，以实现人体下肢运动分类。 为了消除肌电特征冗余及不相关的特征，同时避免单个降维造成特征信号的缺失，分别采用LFDA 有监督降维和LPP 无监督降维，使用改进的GQPSO-KFWELM 对降维后的特征值进行处理，避免正则化系数和核参数对KFWELM 的影响，最后使用决策级融合得到分类结果。 本文方法准确度高，适合用于下肢运动分类。