一种揭示异质无线传感器网络恶意程序传播的动力学模型*

沈士根，杨淑敏，黄龙军，刘建华*，吴国文，张 红，曹奇英

(1.绍兴文理学院计算机科学与工程系，浙江 绍兴312000；2.东华大学计算机科学与技术学院，上海201620)

随着异质无线传感器网络(Heterogeneous WSNs，HWSNs)的应用越来越广泛，HWSNs 中恶意程序传播导致的安全问题日益严峻[1-3]。 由于恶意程序可以根据代码构成实现自我复制的功能，而且恶意程序一旦被激活就可以主动进行传播，使得恶意程序将以指数增长方式四处扩散，严重威胁HWSNs 的数据安全和网络可靠性[4-6]。

要研究HWSNs 恶意程序的传播问题，首先需要通过建模分析HWSNs 恶意程序传播模型，再进一步研究其稳定性，从而揭示HWSNs 恶意程序的传播规律，为恶意程序的防御、传播遏制以及HWSNs 性能安全的提高提供借鉴和参考。 王小明团队[7]较早研究了WSNs 中的恶意程序传播问题，在考虑节点死亡状态基础上扩展传统的SIR 模型得到了iSIRS 传播模型，系统研究了移动传感网中的恶意程序传播问题，建立了基于偏微分方程理论的恶意程序传播时空动力学模型[8]、基于元胞自动机的传播模型[9]以及SIRD 模型[10]，分析了动力学模型的稳定性和分歧性[11]，还很好地综述了传感器网络恶意程序传播模型和遏制方法[12]。 罗小娟等人[13]融合免疫机制，得到了一种改进的SIR 模型。 黄一才等人[14]综合考虑节点通信距离、休眠和隔离状态提出一种包含8 个状态的恶意程序传播模型。 Song 和Zhang[15]提出了具有时滞性质的e-SEIR 模型。 Nowzari 等人[16]以异质节点构成的有向图为基础，提出了一种SEIV(Susceptible-Exposed-Infected-Vigilant)模型。 Zhang 等人[17]提出了一种SAIS(Susceptible-Alert-Infectious-Susceptible)模型并评估了不同警报策略的作用。 Singh 等人[18]考虑WSNs 传感节点通信半径和节点分布密度，提出了一种考虑接种机制的SEIRV(Susceptible-Exposed-Infected-Recovered-Vaccinated)模型。 Acarali等人[19]以基于WSNs 的物联网为基础，建立了一种能综合反映节点处理能力有限、能量有限和节点密度高等物联网特性的IoT-SIS 模型。 Shen 等人[20]扩展传统的SIR 模型从而得到一种反映节点异质特性的SIR 模型，并对模型的稳定性进行了分析。 Liu 等人[21]针对可充电WSNs，提出了一种考虑电源状态的SILS(Susceptible-Infected-Low energy-Susceptible)模型。 其他典型的模型还有HSIORD(Heterogeneous Susceptible-Infected-isOlated-Removed-Deceased ) 模型[22]、 SITPS ( Susceptible-Infected-Traced-Patched-Susceptible)模型[23]、车联网恶意程序随机传播模型[24]、考虑社会属性的物联网恶意程序传播模型[25]、以及反映节点时滞特性[26-27]、空间关联性[28]、干扰攻击传播[29]、攻防博弈[30]的WSNs 恶意程序传播模型。 然而，上述相关文献对WSNs 恶意程序传播过程中节点状态的表述还不全面，对恶意程序传染率的表达没有体现WSNs 的异质特性。

本文提出一种考虑节点潜伏和隔离状态，同时反映节点异质特性的HWSNs 恶意程序传播模型，再分析其稳定性，为揭示HWSNs 恶意程序扩散机制和系统管理员有效抑制HWSNs 恶意程序传播提供理论指导。 首先，根据恶意程序可能潜伏和恶意节点可能被成功检测后隔离的特性，提出一种HWSNs 恶意程序传播模型SEQIRD(Susceptible-Exposed-Quarantined-Infected-Recovered-Dead)；其次，以与单个异质传感器节点(Heterogeneous Sensor Node，HSN)直接通信的节点数，即节点的度，反映其异质特性，建立微分方程，从而反映HWSNs 恶意程序传播过程中具有异质性的传感器节点状态的动态变化过程；然后，根据稳定点的数学特性，计算该模型的稳定点，采用下一代矩阵法计算该模型的基本再生数，并证明该模型无病稳定点的局部渐进稳定性。 表1 从模型优点、缺点、关键贡献等方面对本文模型和现有模型进行了比较。

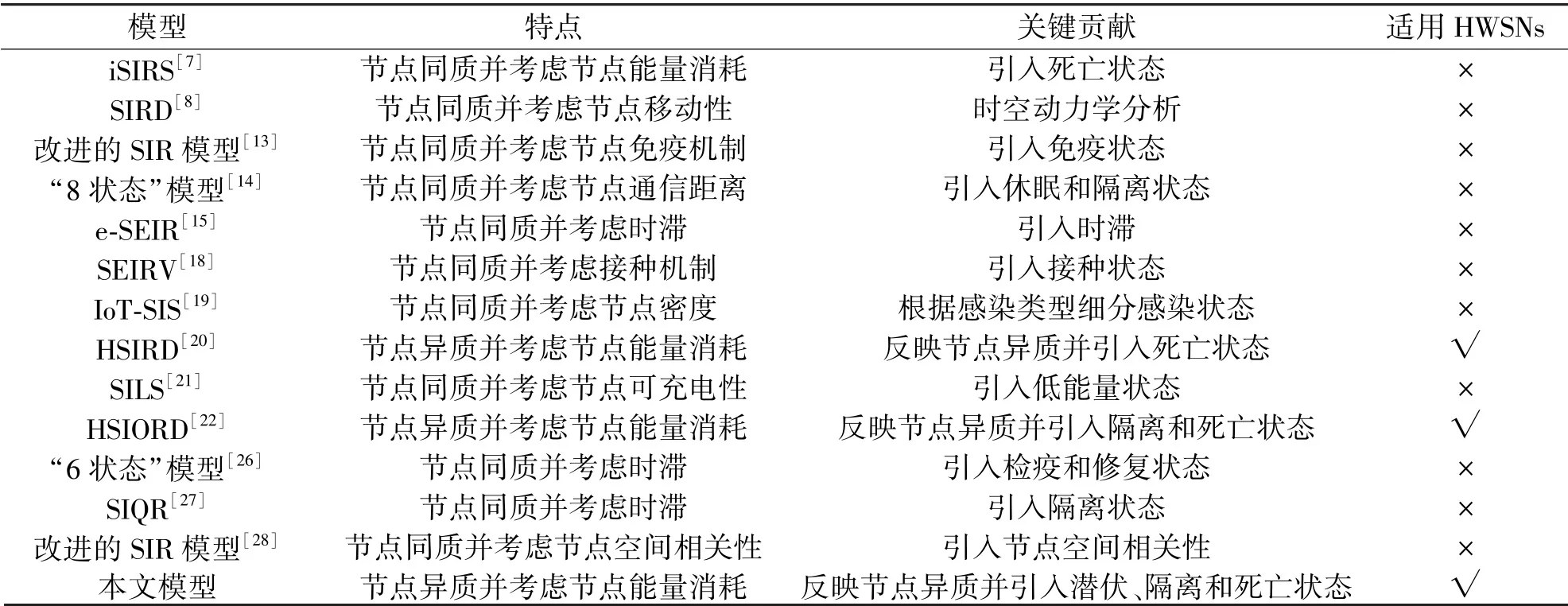
表1 本文模型和现有模型的比较

1 HWSNs 恶意程序传播模型

HWSNs 中的HSN 在被恶意程序攻击而感染前后状态会发生一系列变化，本文共定义六种HSN 状态:易感状态S、潜伏状态E、隔离状态Q、感染状态I、恢复状态R、死亡状态D，如图1 所示。 当HSN 因为安全等级较低而存在漏洞，有被感染风险的时候，所处的状态称为易感状态S；处于易感状态的HSN 被恶意程序感染，但是恶意程序还没有被激活的状态称为潜伏状态E；当HSN 因存在恶意程序而被安全系统发现并隔离时所处的状态称为隔离状态Q；被恶意程序感染的HSN 在与其他节点通信的过程中传播恶意程序时所处的状态称为感染状态I；当HSN 中的恶意程序被安全系统消除，以后不会再受该恶意程序攻击时所处的状态称为恢复状态R；HSN 因为环境影响和能量消耗等因素而不能提供正常服务时所处的状态为死亡状态D。

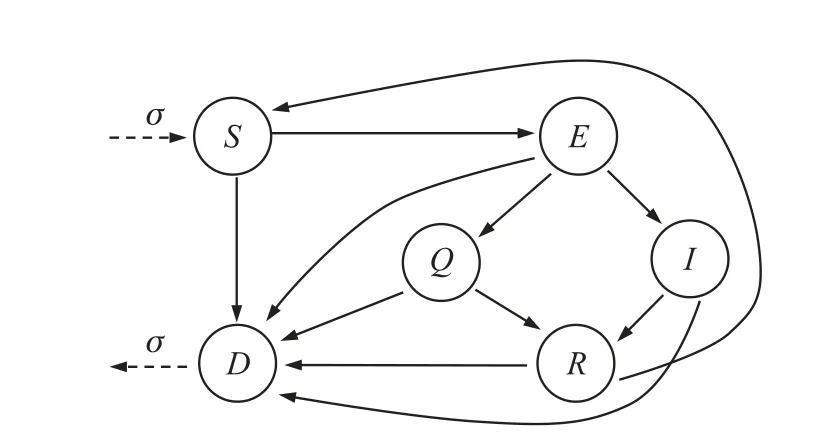
图1 HWSNs 恶意程序传播模型SEQIRD 中节点状态转换图

设一个HWSNs 共包含M个HSN，与一个HSN通信的其他HSN 数量为i(1≤i＜M)个，即该HSN 的度为i。 记Si(t)、Ei(t)、Qi(t)、Ii(t)、Ri(t)、Di(t)表示度为i的HSN 在t时刻分别处于S、E、Q、I、R、D状态的数量占传感器节点总数的比例，则易得:

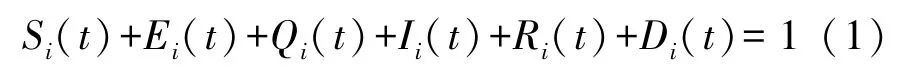
将处于感染状态I且度为i的HSN 初始比例记为o，即

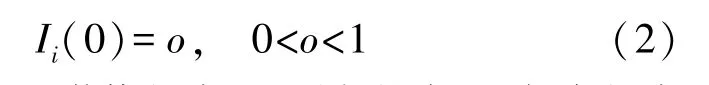
假设分别处于潜伏状态E、隔离状态Q、免疫状态R和死亡状态D且度为i的HSN 初始比例均为0，即

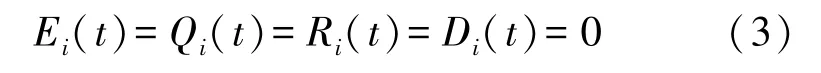
根据式(1)～式(3)，可以得到处于易感状态S且度为i的HSN 初始比例:

在t时刻，处于感染状态的HSN 向周围度为i的易感状态节点传播恶意程序的概率记为Θi(t)，则

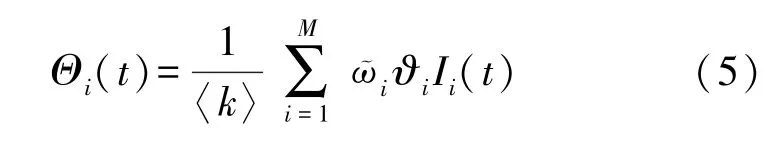
式中:HWSNs 的平均度为〈k〉，HSN 度为i的概率为ῶi，恶意程序被激活启动后处于活跃状态时向其他不存在恶意程序的HSN 发起攻击的概率为ϑi。 而且，参数满足条件:

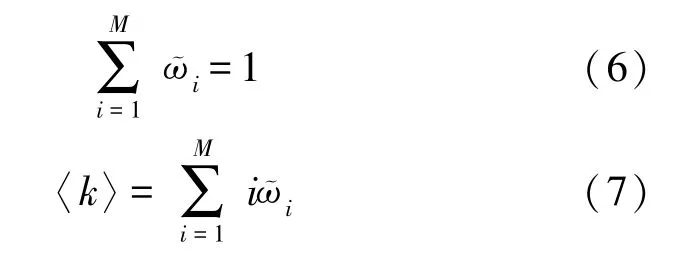
度为i的HSN 从状态x(x∈{S，E，Q，I，R，D})转换到状态y(y∈{S，E，Q，I，R，D})的概率记为qxyi。另外，为了维持整个HWSNs 正常的生命周期，会有比例为σ的度为i且易感的HSN 新接入网络，用于更换一些损坏的HSN 以保证整个HWSNs 正常运行。对处于状态S的HSN，其比例变化值等于σ加上从状态R转换到S的比例，减去从状态S转换到状态E的比例，再减去从状态S转换到状态D的比例，用微分方程可以表示为:

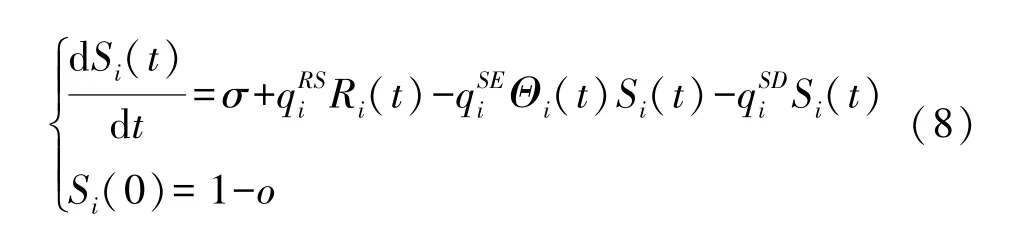
类似地，可以得到描述其他状态比例变化的微分方程为:

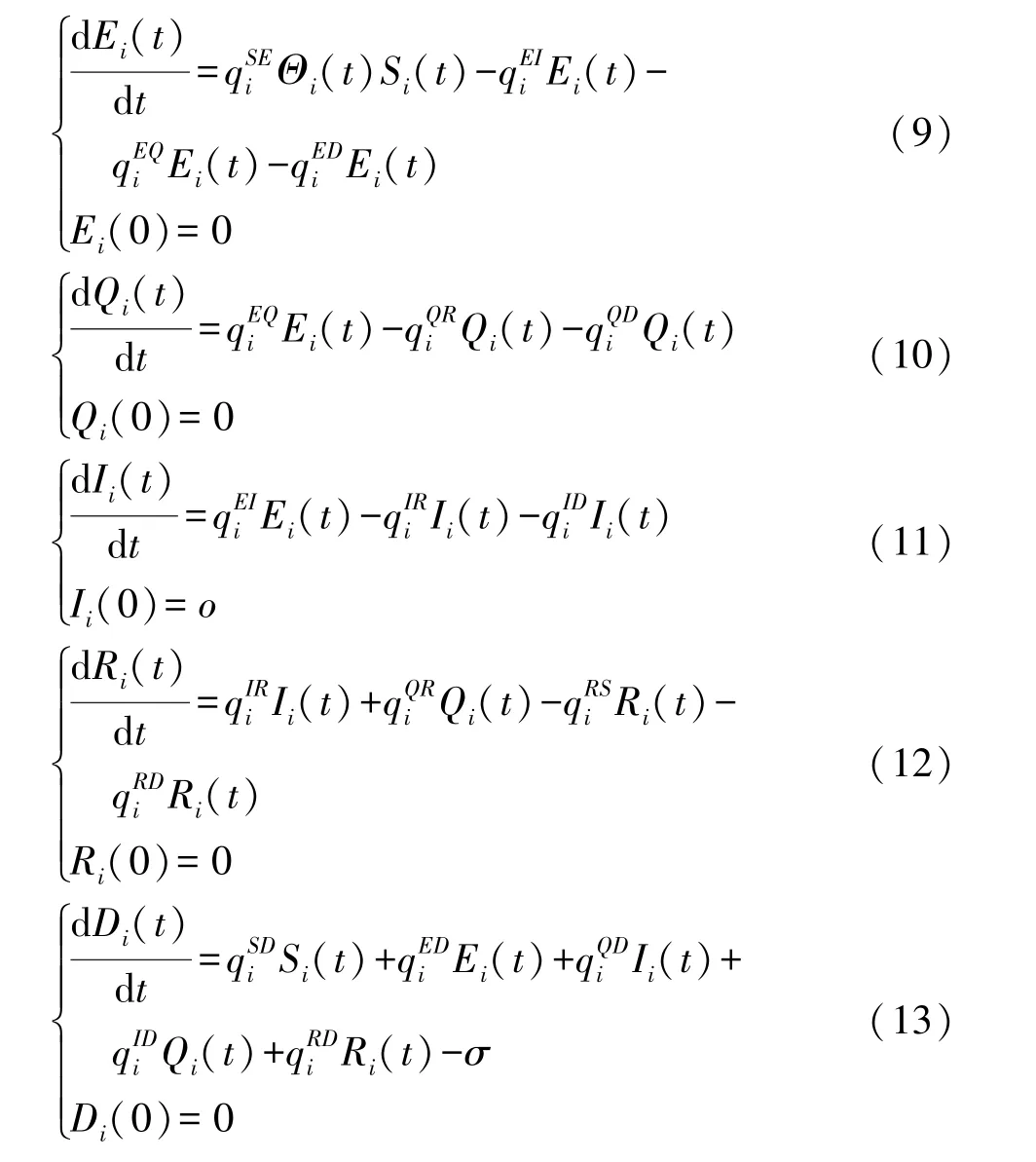
2 恶意程序传播模型SEQIRD 的稳定点

通过计算得到模型SEQIRD 的稳定点，能够确定HWSNs 中恶意程序消亡或传播的阈值，从而能对面向恶意程序传播的HWSNs 防御提供有效的指导。 实际上，求解模型SEQIRD 的稳定点跟求解微分方程组的稳定点一致，具体求解时，令反映各个状态动态变化的微分方程值为0 后形成方程组，再求解该方程组即可得到模型SEQIRD 的稳定点。

定理1面向恶意程序传播的模型SEQIRD 存在稳定点。

证明当模型SEQIRD 中反映各节点状态动态变化的微分方程达到稳定点时，各节点状态动态变化值均为0，即:

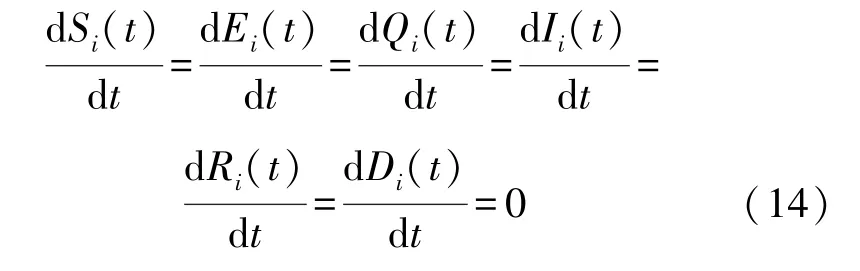
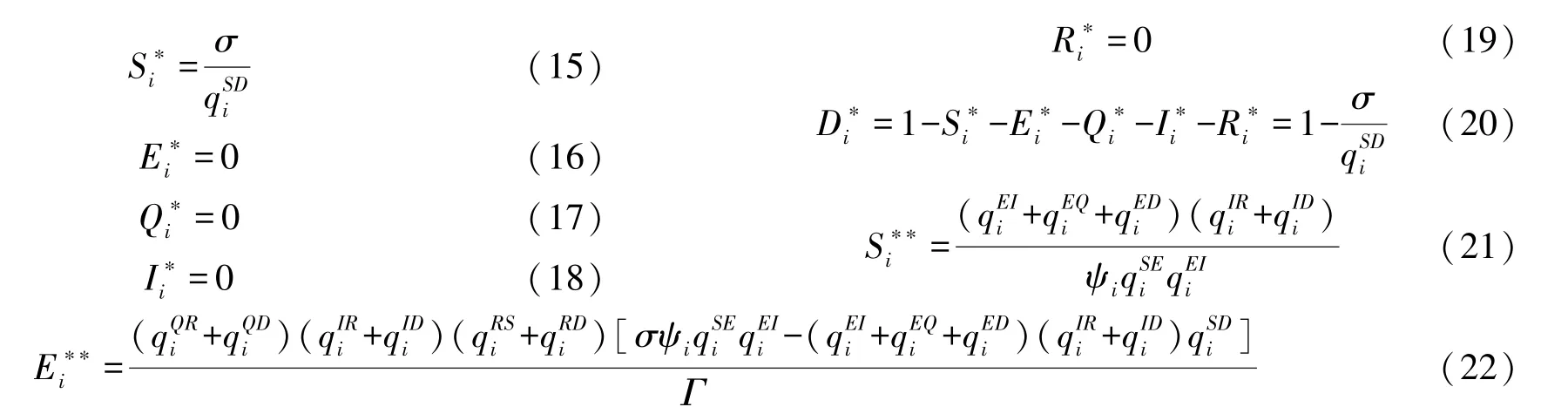
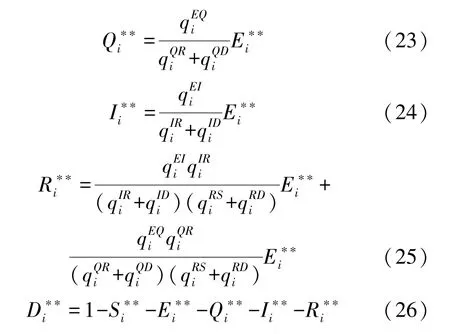
式中:

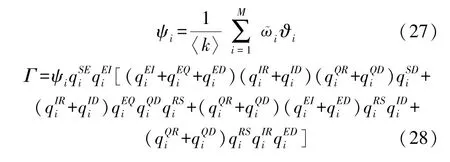
证毕。

定理1 得到的稳定点O*和O**含义不同。 其中，稳定点O*称为无病稳定点，即I*=0，表示整个HWSNs 达到稳定点O*后被恶意程序成功攻击感染的HSN 已不存在，也就是说，HWSNs 恶意程序最终将消亡。 稳定点O**称为有病稳定点，即I**＞0，表示整个HWSNs 达到稳定点O**后被恶意程序成功攻击感染的HSN 将大量存在，也就是说，恶意程序在整个HWSNs 中将处于传染状态。 因此，实际的HWSNs应用场景中，系统管理员应该采取相应的防御措施使得HWSNs 恶意程序传播模型SEQIRD 趋向于无病稳定点O*，从而抑制HWSNs 恶意程序的传播。

3 恶意程序传播模型SEQIRD 的基本再生数

通过探寻HWSNs 恶意程序传播模型SEQIRD的基本再生数，能以此判断被恶意程序成功攻击并感染的HSN 能够感染其他与其直接通讯的节点的平均个数。 若基本再生数的值小于1，则表明一个被恶意程序成功攻击并感染的HSN 能感染与其直接通讯的易感节点的个数少于1 个，这将使整个HWSNs 趋向于无病稳定点O*；若基本再生数的值大于1，则表明一个被恶意程序成功攻击并感染的HSN 能感染与其直接通讯的易感节点个数大于1，这将使整个HWSNs 趋向于有病稳定点O**。 所以，计算得到模型SEQIRD 的基本再生数就能确定HWSNs 趋向于无病稳定点O*的条件，从而为系统管理员防御HWSNs 恶意程序传播指明方向。

本文基本再生数的计算采用下一代矩阵法。 记ζ为HWSNs 恶意程序传播模型SEQIRD 的基本再生数，则ζ=ρ(FV-1)，其中，ρ(·)代表矩阵的谱半径，F代表当前HWSNs 在无病稳定点O*处状态I的新增HSN 动态变化率矩阵，V代表HWSNs 在无病稳定点O*处状态任意的两个HSN 之间的动态转换率矩阵，V-1代表矩阵V的逆矩阵。 通过这种方法计算恶意程序传播阈值需要用到状态E和状态I，为了清楚地描述F、V的计算过程，引入临时变量A、B、a11、a21、b11、b21。 令:

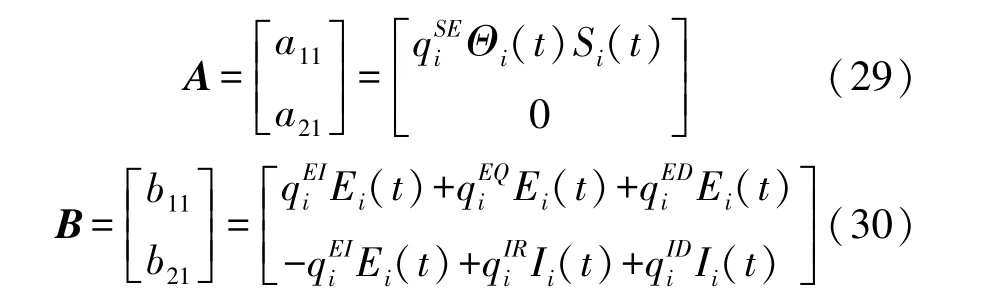
由式(29)可以得到新增HSN 动态变化率矩阵F为:

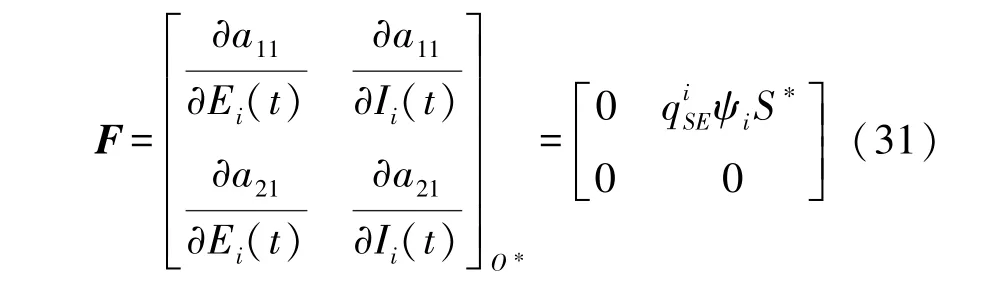
由式(30)可以得到动态转换率矩阵V为:

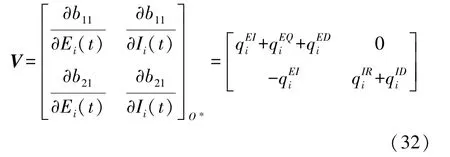
因此，可以得到HWSNs 恶意程序传播模型SEQIRD的基本再生数ζ为:

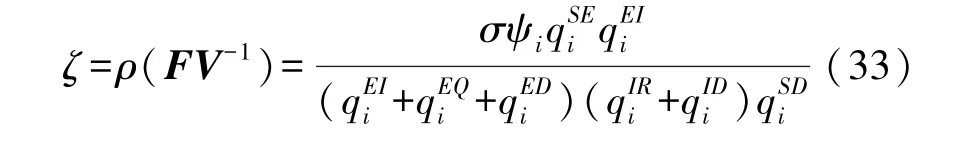
4 恶意程序传播模型SEQIRD 的稳定性分析

对于HWSNs 恶意程序传播模型SEQIRD 的稳定点O*和O**，只有系统管理员采取安全防御措施使模型SEQIRD 趋向于无病稳定点O*，才能有效控制HWSNs 恶意程序的传播。 所以，本文仅研究无病稳定点O*的稳定性。

定理2当ζ＜1 时，HWSNs 恶意程序传播模型SEQIRD 的无病稳定点O*局部渐进稳定；而当ζ＞1时，无病稳定点O*不稳定。

证明HWSNs 恶意程序传播模型SEQIRD 的雅克比矩阵J为:

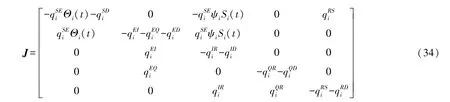
进一步，得到在无病稳定点O*的雅克比矩阵J(O*)为:

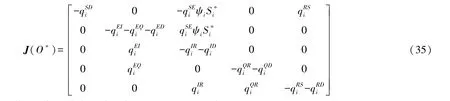
记λ代表特征值，E代表单位矩阵，则J(O*)对应雅克比行列式的三个特征值为:

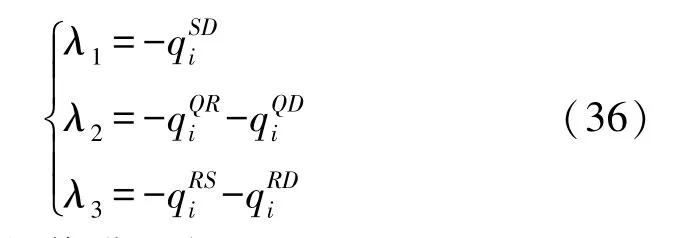
另外两个特征值满足方程:

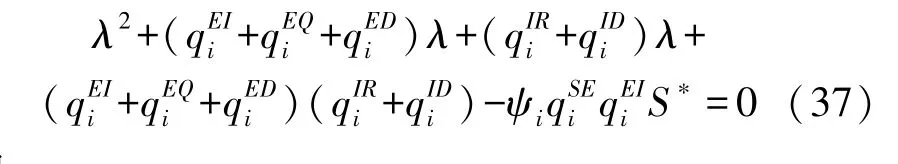
式中:

记

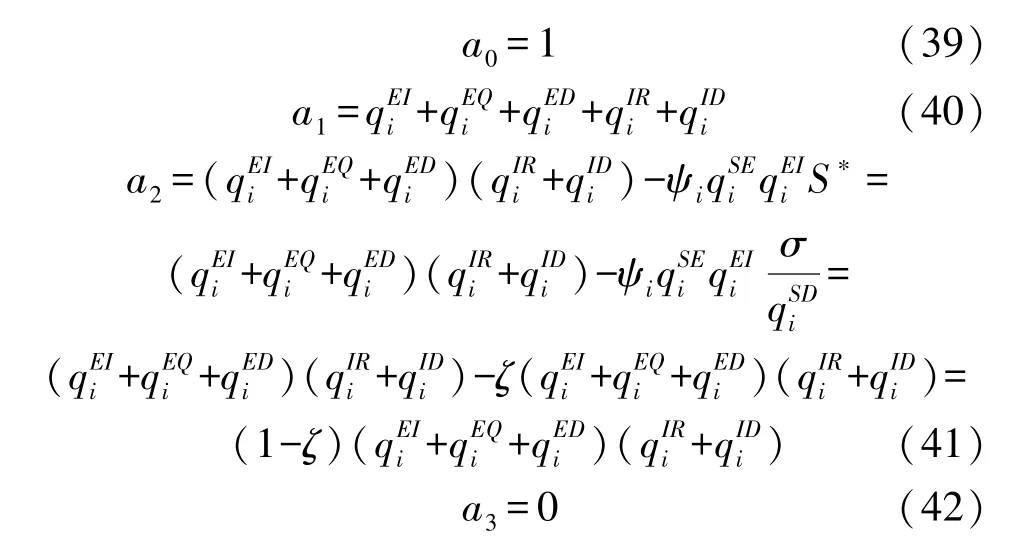
根据Routh-Hurwitz 判据[18]可知，

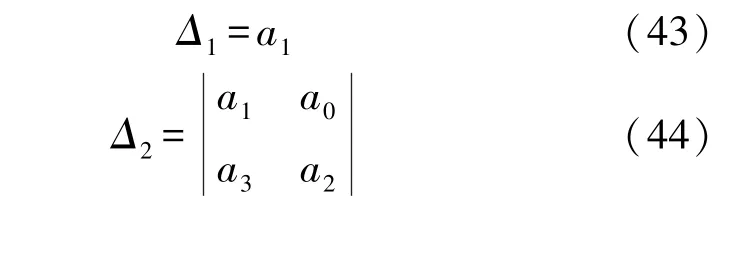
当Δ1和Δ2均大于0，即当a1＞0，a1a2-a0a3＞0时，方程对应的矩阵存在负实部特征值。 显然，当ζ＜1时，满足a1＞0，a1a2-a0a3=a1a2＞0，由Lyapunov稳定性定理可得，HWSNs 恶意程序传播模型SEQIRD 的无病稳定点O*是局部渐进稳定的；而当ζ＞1 时，a1＞0，a1a2-a0a3=a1a2＜0，方程对应矩阵的特征值没有负实部，所以，HWSNs 恶意程序传播模型SEQIRD 的无病稳定点O*是不稳定的。 证毕。

定理2 结论揭示当ζ＜1 的时候，处于状态S、E、Q、I、R、D且度为i的HSN 所占比例Si(t)、Ei(t)、Qi(t)、Ii(t)、Ri(t)、Di(t)最终分别趋向于、0、0、0、0、。 即当条件ζ＜1 满足时，不管HWSNs 中已经被恶意程序成功攻击并感染的HSN 的初始比例如何，只要系统管理员能够保持目前的安全防御措施，HWSNs 恶意程序最终能被彻底清除，这对HWSNs 安全防御具有现实指导意义。

5 仿真及分析

通过仿真软件MATLAB，验证HWSNs 恶意程序传播模型SEQIRD 无病稳定点O*的稳定性，以及关键转换概率和对HWSNs 恶意程序传播的影响。 具体仿真时，先将模型SEQIRD 变换成离散形式，即:

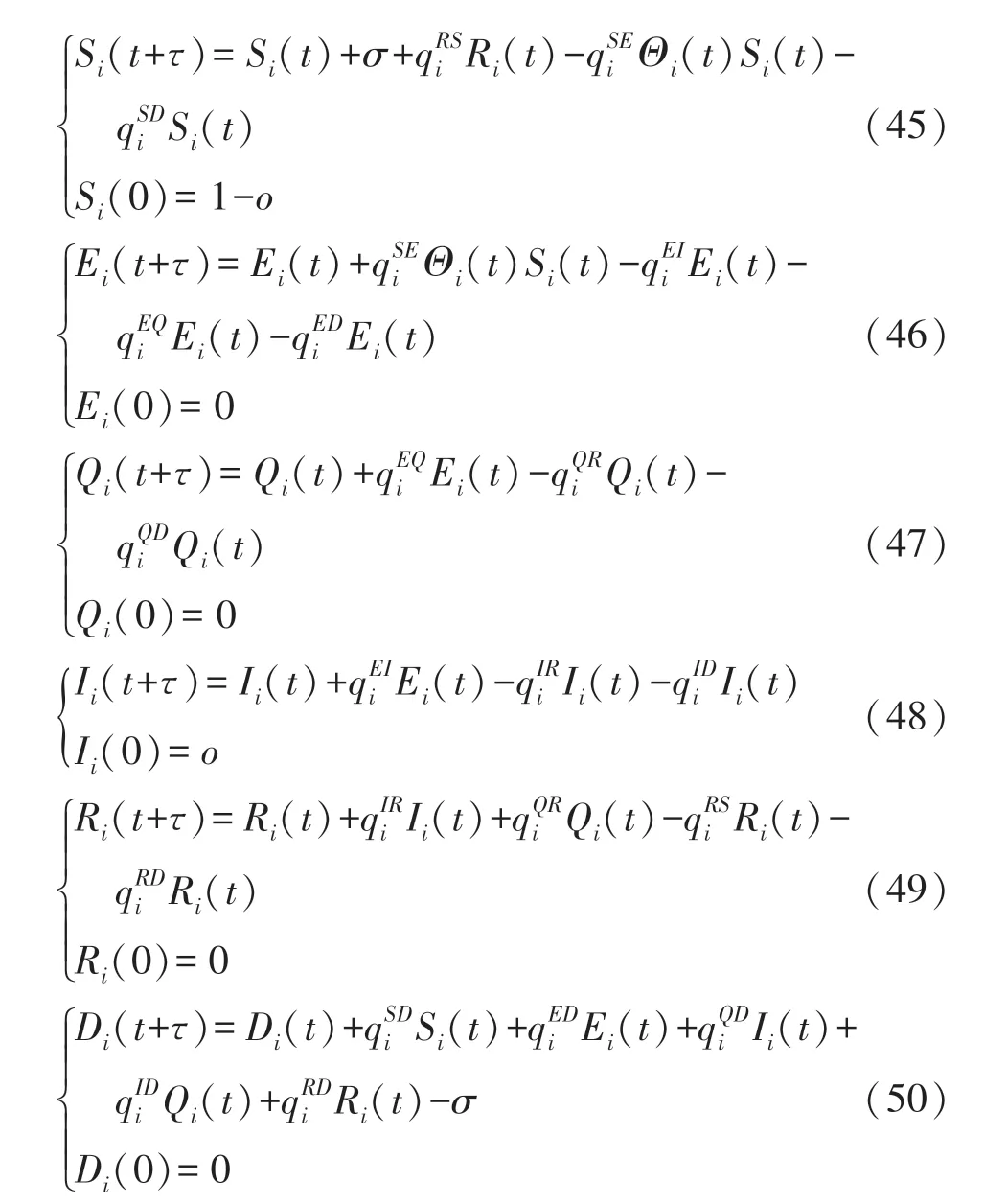
式中:τ代表离散的时间间隔。 这样，通过使用Runge-Kutta 方法即可求解离散形式的SEQIRD 模型。 具体的仿真算法如算法1 所示。

算法1 验证HWSNs 恶意程序传播模型SEQIRD 的算法

仿真实验中设置参数如下:M= 1000，表示HWSNs 中包含1000 个HSN；τ=1 h，表示离散的时间间隔是1 h。 一个HSN 的最小度为2，最大度为20，并且〈k〉=4，即HSN 的平均度为4。 一个HSN 被恶意程序成功攻击并感染使状态从S状态转换为E状态的转换率设置为βi，其中，β=0.01。 被恶意程序成功攻击并感染的一个HSN，处于易感状态的概率ϑi设置为ξiγ/(1＋μiγ)，其中，ξ=5，γ=0.5，μ=1。 根据HWSNs 的特性，其他参数分别设置为σ=0.01，=0.015。

5.1 验证无病稳定点的稳定性

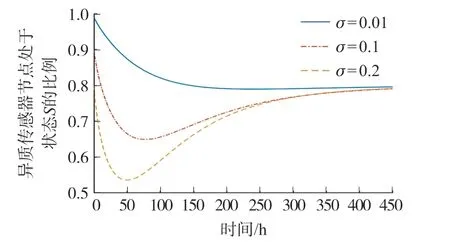
图2 处于状态S 的HSN 比例变化趋势

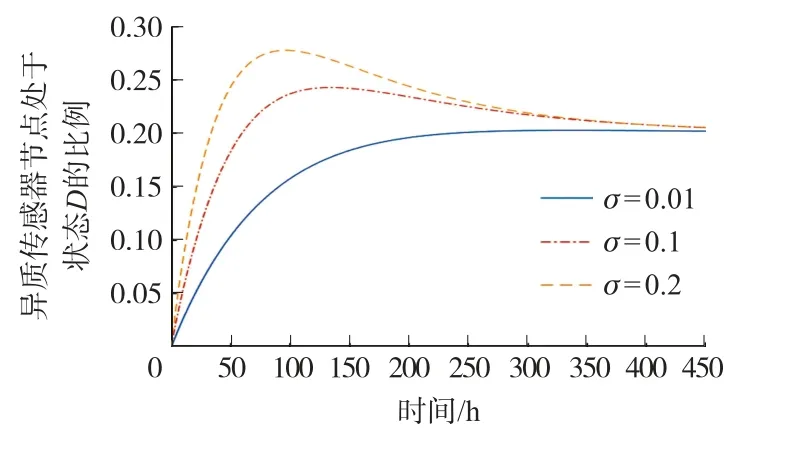
图7 处于状态D 的HSN 比例变化趋势

在图2 中，处于状态S且度为i的HSN 比例Si(t)在不同的o取值下呈现不同的变化趋势。 当o为1%的时候，Si(t)缓慢减少至约80%后，趋于稳定；当o为10%的时候，Si(t)缓慢减少至最低值约65%后，再缓慢上升最后稳定于约80%；当o为20%的时候，Si(t)缓慢减少至最低值约54%后，再缓慢上升最后稳定于约80%。 也就是说，最终Si(t)趋向于无病稳定点中的值0.8。

在图3～图6 中，处于状态E、Q、I、R的HSN 比例Ei(t)、Qi(t)、Ii(t)、Ri(t)的变化趋势在不同的o取值下保持一致。 由图3 可以看出，Ei(t)逐步上升分别达到最高值约0.8%、6%和9.6%后，再缓慢下降最后趋向于0，这和无病稳定点中的值保持一致。 由图4 可以看出，Qi(t)逐步上升分别达到最高值约0.3%、2.1%和3.1%后，再缓慢下降最后趋向于0，这和无病稳定点中的值保持一致。由图5 可以看出，Ii(t)呈现下降趋势最后趋向于0，这和无病稳定点中的值保持一致。 由图6 可以看出，Ri(t)逐步上升分别达到最高值约1%、6%和9.3%后，再缓慢下降最后趋向于0，这和无病稳定点中的值保持一致。

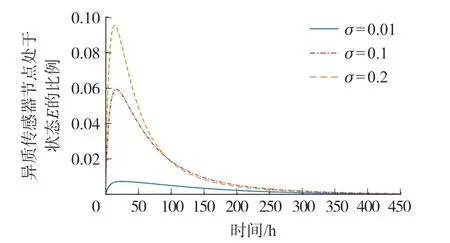
图3 处于状态E 的HSN 比例变化趋势

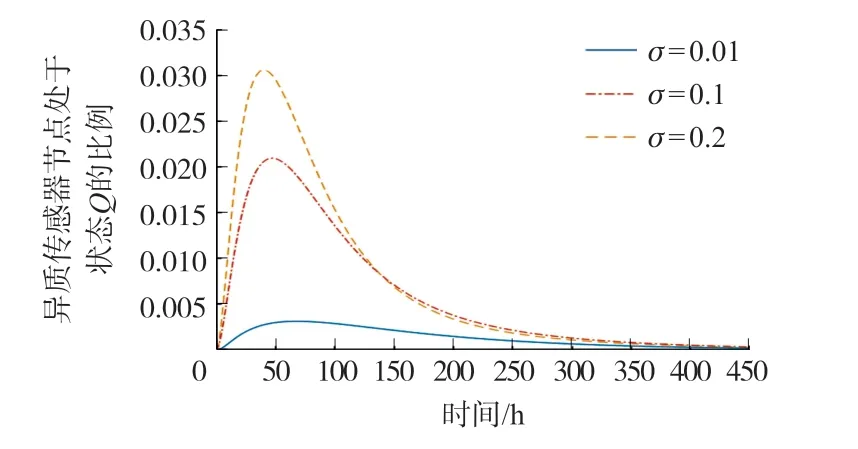
图4 处于状态Q 的HSN 比例变化趋势

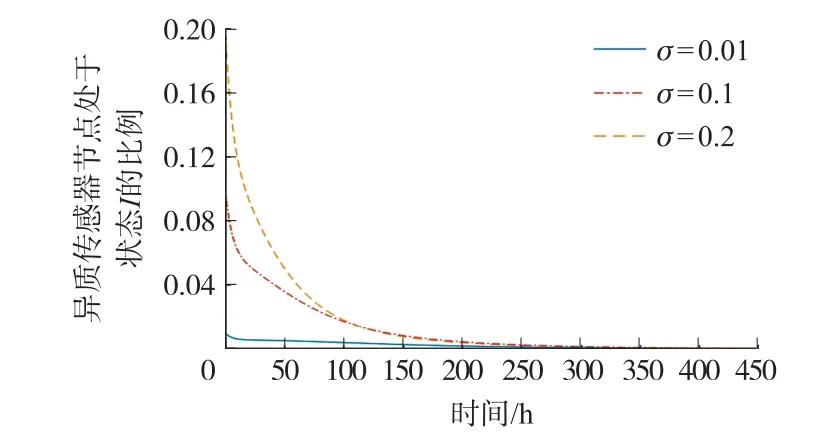
图5 处于状态I 的HSN 比例变化趋势

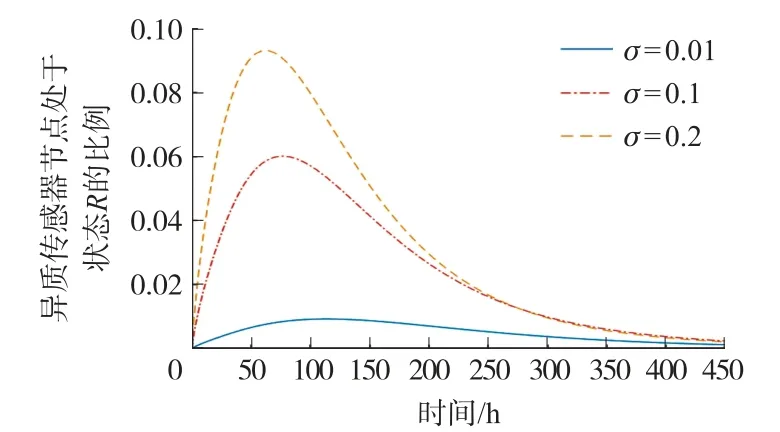
图6 处于状态R 的HSN 比例变化趋势

在图7 中，处于状态D且度为i的HSN 比例Di(t)在不同的o取值下呈现不同的变化趋势。 当o为1%的时候，Di(t)缓慢上升至约20%后趋于稳定；当o为10%的时候，Di(t)缓慢上升至最高值约24%后，再缓慢减小比例最后稳定于约20%；当o为20%的时候，Di(t)逐渐增大至最高值约27%后，比例再逐渐减小，最后稳定于约20%。 也就是说，最终Di(t)趋向于无病稳定点中的值0.2。

从而验证了不管处于状态I的HSN 初始比例设置值如何，只要满足基本再生数ζ值小于1 的条件，经过恶意HSN 的反复攻击感染和反复传播，以及系统管理员采取相应的防御措施，对恶意HSN 的反复攻击感染和反复传播进行抑制，处于状态S、E、Q、I、R、D且度为i的HSN 比例最终将分别趋向于无病稳定点。 实验结果反映出在现实的HWSNs 管理过程中，系统管理员采取的安全防御措施要能影响并控制HWSNs 中的参数，达到定理2 中基本再生数值小于1 的条件，使得HWSNs 即使存在大量初期被恶意程序成功攻击并感染的HSN，其中的恶意节点都将被治愈，从而有效控制HWSNs 恶意程序的传播。

5.2 状态转移概率和对HWSNs 恶意程序传播的影响

由式可知，一旦HWSNs 拓扑结构固定下来后，状态转移概率等参数值也相对固定，而状态转移概率和两个参数变化较大，因此，本节通过仿真分析和对HWSNs 恶意程序传播的影响，为系统管理员控制HWSNs 恶意程序传播提供实验依据。 实验采用变量控制的思想，即将处于状态I且度为i的HSN 初始比例设置为10%，其他状态转移概率参数的值保持不变，分别调整状态转移概率和参数值得到不同的仿真结果，再进行分析。

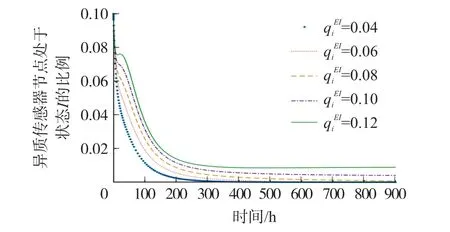
图8 处于感染状态I 且度为i 的HSN 比例在不同参数值下的变化曲线

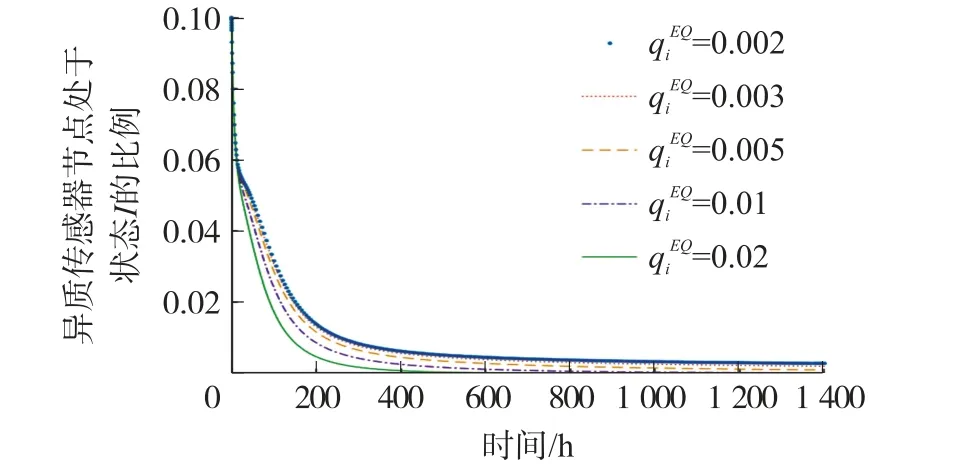
图9 处于感染状态I 且度为i 的HSN 比例在不同参数值下的变化曲线

6 结论

在扩展传统传染病模型SIR 基础上，构建了基于潜伏和隔离机制的HWSNs 恶意程序传播模型SEQIRD，分析了HWSNs 恶意程序的传播特性。 通过引入单个HSN 的度来反映该节点异质的通信能力特性，解决了未体现HSN 异质特性的现有传染病模型不能用于HWSNs 恶意程序传播建模的问题。得到的HSN 状态动态变化方程解决了现有模型没有充分考虑HWSNs 恶意程序传播具有隐蔽性、恶意HSN 被成功检测而被隔离、HSN 因被恶意程序感染导致恶意破坏或自然损坏等情形的问题。 通过计算得到的模型SEQIRD 的稳定点以及基本再生数，明确了HWSNs 恶意程序消亡或传播的阈值，进一步得到的HSN 易感状态到潜伏状态和隔离状态的转换概率阈值，为系统管理员制定一系列安全防御策略，从而遏制HWSNs 恶意程序传播，并保证HWSNs 稳定、健康运行奠定理论基础。

需要说明的是，本文考虑的HWSNs 恶意程序属于同一种类型，而通常HWSNs 存在不同的恶意程序，因此，如何揭示HWSNs 中不同恶意程序的传播机制是研究者值得进一步研究的实际问题。 另外，本文在借鉴经典传染病模型思想时，考虑新加入的是易感节点，但如果加入的是打了安全补丁的节点，那么将得到用于描述状态比例变化的不同的微分方程、不同的模型稳定点、不同的基本再生数，这样得到的新模型是否还能保证稳定? 该问题符合实际的HWSNs，也是值得进一步研究的问题。