配电网变电站经济供电半径研究

程军照，李芳方，莫海峰，徐 敏，袁智勇

配电网变电站经济供电半径研究

程军照1，李芳方1，莫海峰1，徐 敏2，袁智勇2

(1.云南电网有限责任公司电网规划建设研究中心，云南 昆明 650011；2.南方电网科学研究院，广东 广州 510080)

为减少规划投资并提高供电质量，针对变电站经济供电半径进行了研究。首先，构建了考虑变电站建设投资和运维费用并以单位供电面积年费用最小为目标函数的变电站供电半径优化模型，研究了变电站经济供电半径求解算法。其次，建立了不同负荷情形下的变电站供电半径和线路电压损失之间的定量关系，在此基础上根据配电网对电压损失的规定对优化计算得到的经济供电半径进行电压质量校验。通过对实际电网数据的测算，验证了算法的准确性和合理性。计算结果可为地区配电网规划提供有效的参考。

配电网；变电站；规划；经济供电半径；线路电压损失

0 引言

随着社会经济的发展，在提高中压配电网供电能力的同时，对中压配电网运行方式的可靠性和灵活性等提出了更高的要求[1-5]。网架结构的合理性决定了中压配电网运行的可靠性和未来的发展空间，合理的供电半径是确定中压配电网网架布局的重要因素之一。供电半径的选择不仅直接影响配电网的电能质量，还影响着配电网中变电站和线路的投资及运行费用[6]。

以往研究中，通过电能质量极限值核算供电半径的方法[7-9]，忽略了配电网经济性的要求，因此越来越无法满足配电网规划建设的需要。目前对于变电站供电半径的优化研究是基于以单位面积年费用最小为目标函数[10-12]，以各项技术指标为约束条件的方法计算最优供电半径[13]。

文献[14]建立以总费用最小为目标函数、以变电站满足“-1”准则为约束条件的变电站优化模型。采用该优化模型可分别计算得到变电站最优容量、变压器最优台数和变电站最优供电半径，但前提条件是已知三者中的两个，这限制了该模型的应用场景。文献[15]在建立单位容量年费用函数过程中，采用固定值衡量变压器运行时的电能损失费用，未对计算得到的变电站最优供电半径进行电能质量检验，会影响计算结果的准确性与合理性。文献[16-19]分别引入动态规划思想、柔性规划理念和加权Voronoi图算法改进变电站供电半径的优化模型，但都未考虑负荷同时率对容载比的影响，其计算结果会降低变压器等设备的利用率[20]。文献[21-24]提出了混合启发式和学习自动机算法，采用静态和动态规划方法建立变电站选址定容优化模型，但对变电站供电范围的划分较粗糙，无法保证变电站负载的均衡性。文献[25-26]研究了配电网投资效益综合评估方法和评估模型，涉及多个指标维度的综合分析，但未对变电站经济供电半径进行详细分析。

针对以上问题，本文将在不同负荷密度下，建立基于单位面积年总费用最小的变电站供电半径优化模型。通过线性回归拟合得到变压器的电能损耗费用与实际负载的函数关系，同时考虑负荷同时率对变电站容载比的影响，并且对最优计算求得的经济供电半径在不同负荷分布场景下进行电压偏差校验，实现基于差异化原则确定变电站经济供电半径，兼顾中压配电网经济性和电能质量的要求。

1 基于年费用最小的变电站供电半径

1.1 假设条件

本文采用以单位供电面积年投资费用最小为目标函数，建立变电站供电半径算法模型。在建立模型过程中，需要设定如下假设条件：

1) 近似认为供电区域内的目标电网电力负荷均匀分布，变电站的供电区域为圆形，变电站置于圆心。

2) 投资过程中不考虑资金的动态性，建设费用分年等量投入，运行费用在当年的某一负荷水平下一次性投入。

1.2 目标函数

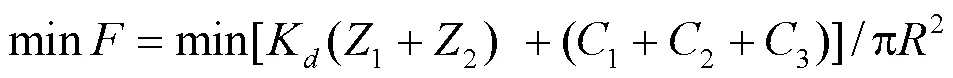
1.2.1建设投资费用

1) 变电站建设投资费用

2) 中压配电网线路建设投资费用

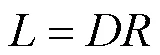
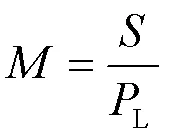
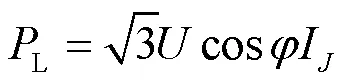
基于容载比，考虑负荷同时率，则有

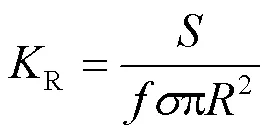
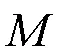
负荷同时率可以衡量线路负荷的变动情况，以及考察变压器的利用情况，其定义为电力系统综合最大负荷与各部分最大负荷之和的比值。根据文献[27]可以得到不同情况下的负荷同时率，如表1所示。

对于不同供电地区，由于负荷组成不同，可由地区电网历史数据计算实际的同时率。

表1 负荷同时率

1.2.2维护运行费用

1) 维护费用

2) 中压出线线路年损耗费用

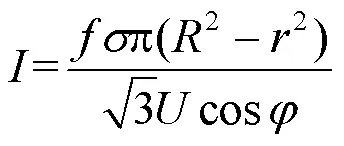
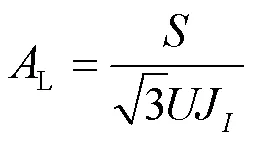
将式(8)、式(12)和式(13)代入式(14)，得到

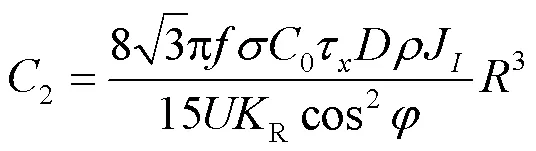
3) 变压器年损耗费用

变压器年损耗费用的表达式为

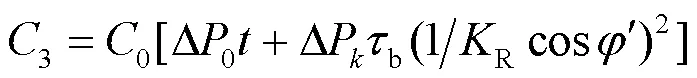
可通过线性回归拟合得到变压器空载损耗与其容量之间的关系，如式(17)所示。

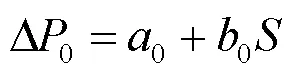
变压器负载损耗模型可以拟合为

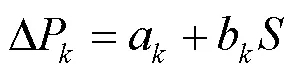
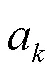
变压器空载和负载损耗模型经校验计算，满足工程精度要求，可以用于变压器供电半径的推导和计算。

1.3 模型求解

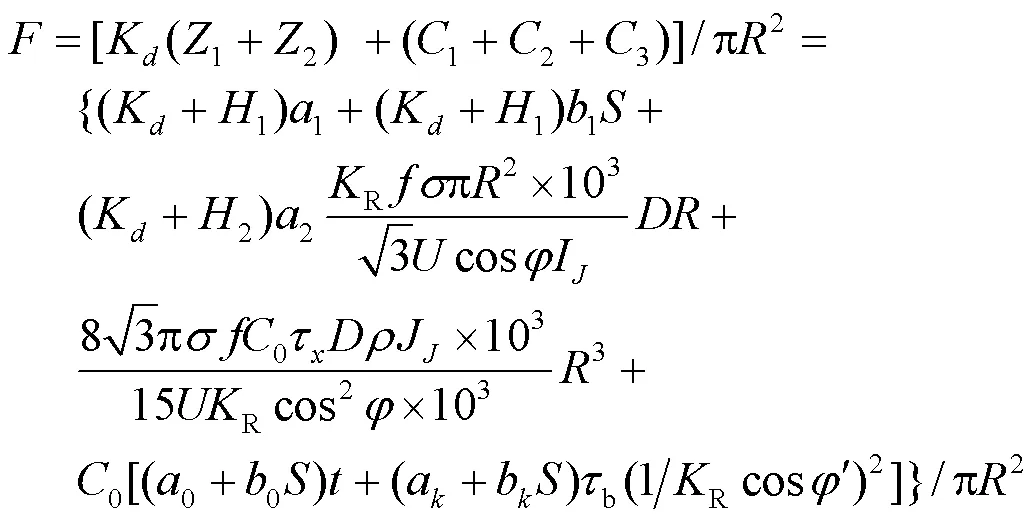
令

则目标函数可表示为

对式(20)求导，得

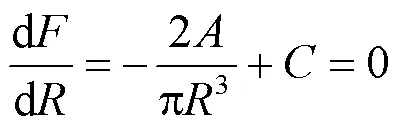
由此可以获得使单位供电面积年投资费用最小的最佳供电半径为

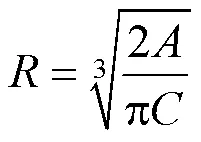
可知，最佳供电半径与负荷密度、容载比、负荷同时率和最大负荷损耗时间等参数相关。

2  基于线路电压损失约束的变电站供电半径算法

电压降需保障变电站出线末端电压水平满足电能质量标准，根据电路理论，电压降为

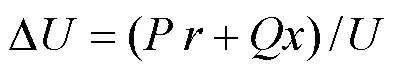
单回出线线路所带负荷可以表示为

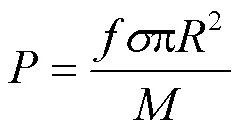
代入式(23)可以得到

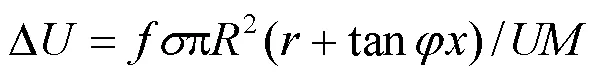
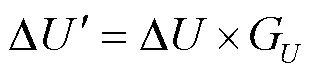
表2 不同负荷分布的电压损耗系数表

参考配电网对10 kV线路电压损失范围的规定，获得

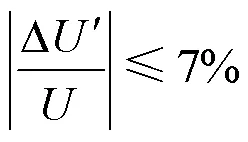
即可得到满足电压降约束的供电半径取值范围。

综上所述，配电网变电站最优供电半径计算流程如图1所示。

图1 配电网变电站经济供电半径算法流程图

3 算例分析

3.1 算例数据

1) 变压器数据

变压器损耗表如表3所示。由表3可绘制得到变压器的空载损耗、负载损耗与变压器容量的关系曲线，分别如图2和图3所示。

由图2可以看出，变压器空载损耗与容量存在一阶线性关系，通过拟合可获得变压器空载损耗模型为

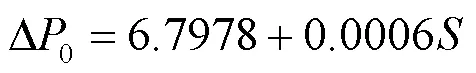
由图3可以看出，变压器负载损耗与容量存在一阶线性关系，通过拟合可获得变压器负载损耗模型为

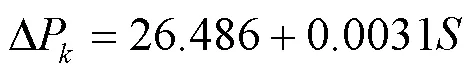
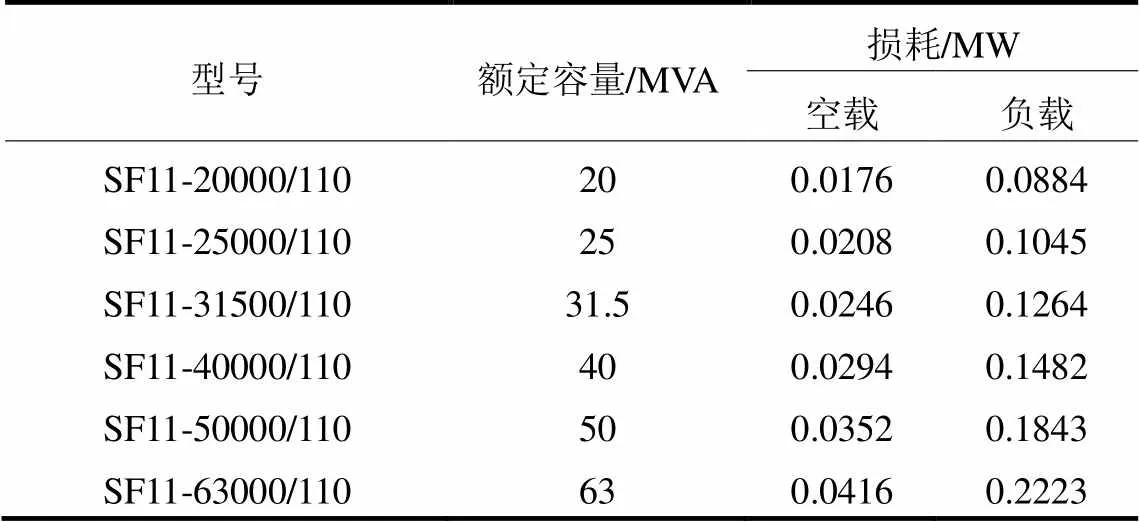
表3 变压器损耗表(SF11)

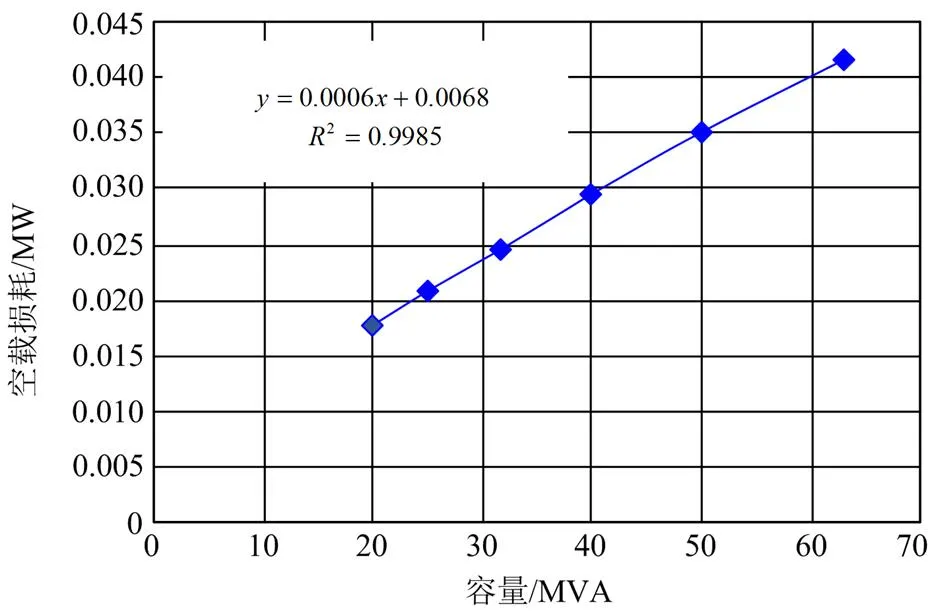
图2 变压器空载损耗与变压器容量的关系图

图3 变压器负载损耗与变压器容量的关系图

2) 投资数据

参考配电网规划的投资单价，可测算得到变电站投资与变电站总容量之间的关系曲线如图4所示。

由图4可以看出变电站建设投资模型为

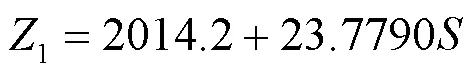
3) 参数选取

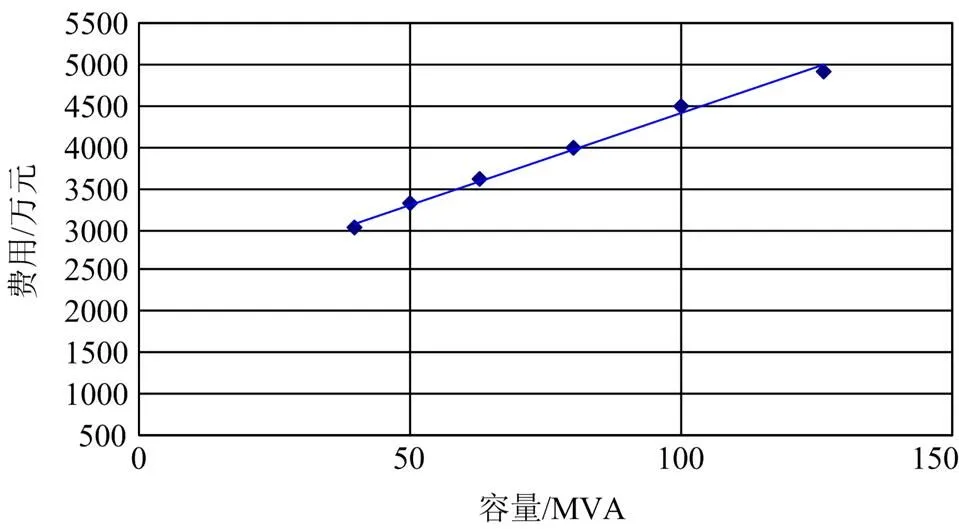
图4 变电站投资与变电站总容量的关系图

3.2 算例结果及分析

3.2.1单位面积年费用最小法计算结果

变电站投资及线路投资在最优供电半径选取中有重要地位，但是在变电站投资高的情况下，线路投资也较高，相互抵消了对供电半径的影响。为确保投资数据的准确性、真实性，投资数据参考实际地区配电网规划的单位工程综合造价。

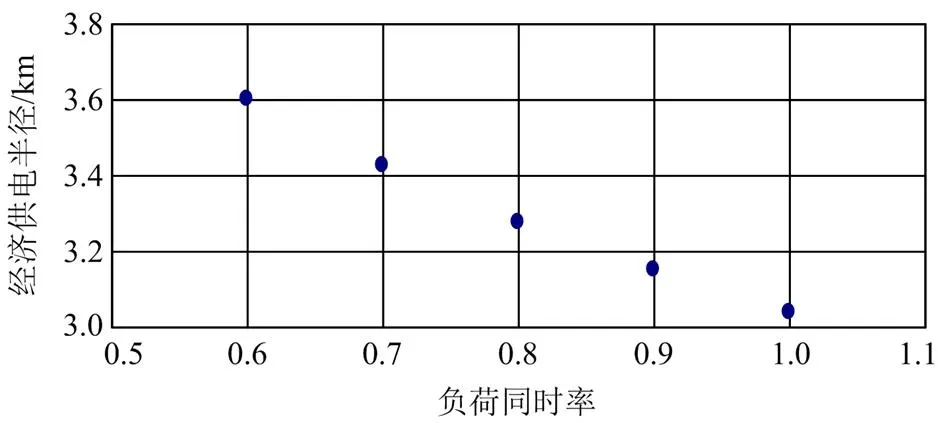
图5 经济供电半径随负荷同时率变化图

由图5 可见，当负荷同时率递增时，经济供电半径的取值递减。在负荷密度一定的情况下，负荷同时率越高，变电站最大负荷越大，线路负荷越重，线路经济供电半径相应减小。

2) 当其他参数不变时，经济供电半径随容载比变化情况如图6所示。

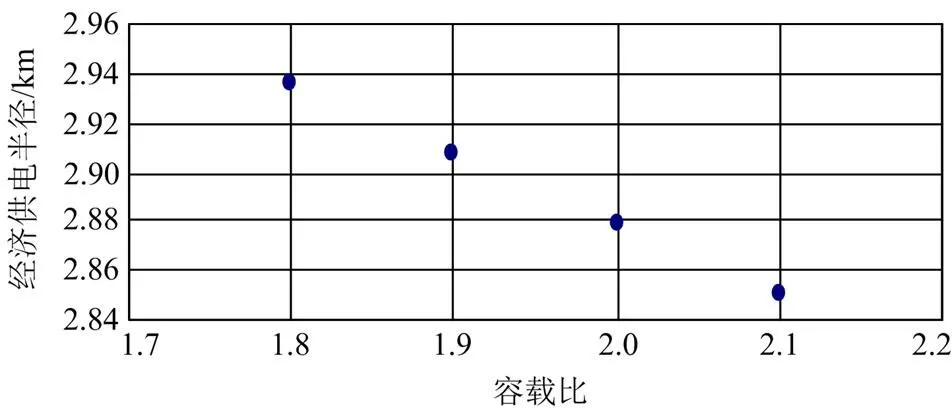
图6 经济供电半径随容载比变化图

由此可见，当容载比递增时，经济供电半径的取值递减。当容载比变化时，地区变电站总的配置容量也随之发生变化，变电站和线路建设总投资和维护费用、损耗及相应运行费用也随着变化，最终使容载比与经济供电半径成反比的关系。

3) 当其他参数不变时，供电半径随最大负荷利用小时数变化情况如图7所示。

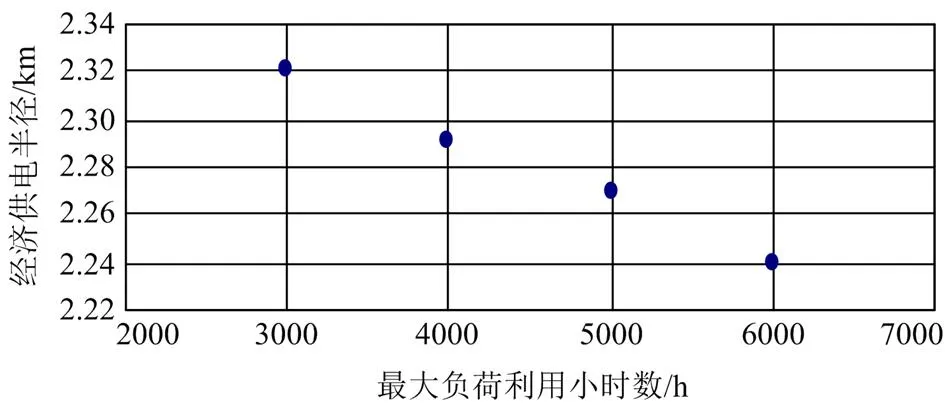
图7 经济供电半径随最大负荷利用小时数变化图

由此可见，最大负荷利用小时数对供电半径的计算影响较小，当最大负荷利用小时数递增时，经济供电半径的取值递减。最大负荷利用小时数与变压器损耗和线路损耗有关，其中起主要作用的是线路损耗，所以供电半径随最大负荷利用小时数的增大而减小。在实际电网运行状况下，最大负荷利用小时数取值范围为3000～6000 h。

4) 10 kV线路经济电流密度与导线型号、最大负荷利用小时数有关，其值在0.8～1.3之间，本次测算中将线路经济电流密度取为常用值1.05。

5) 线路的投资会影响经济供电半径的求取。

表4给出了常用的线路型号及其单价。

当线路选LGJ-150的情况下得到经济供电半径的高值，当线路选YJV-240的情况下得到经济供电半径的低值。

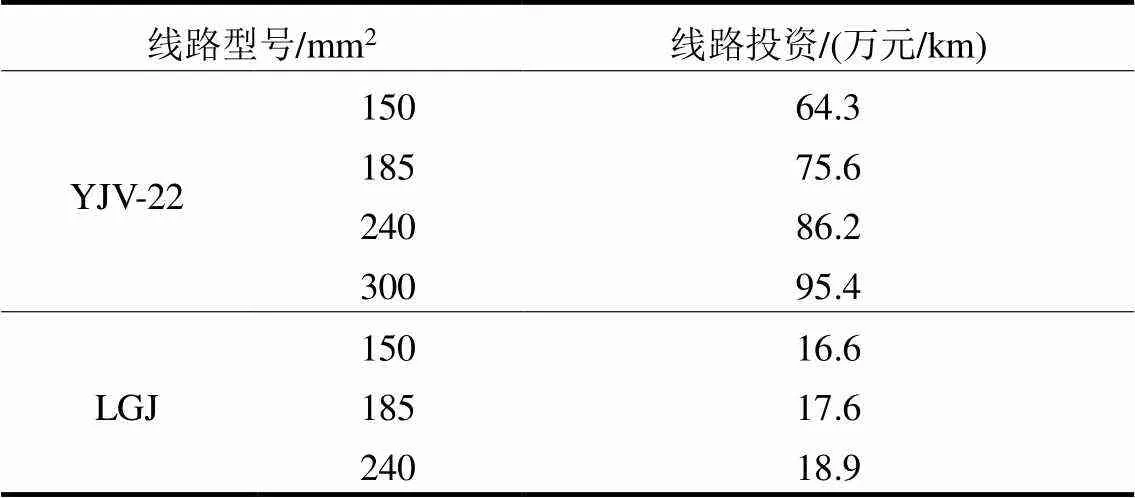
表4 线路型号单价推荐表

通过分析可知，对供电半径范围影响较大的参数是容载比、负荷同时率及负荷密度。参考表5所示的供电区域负荷密度划分，采用单位面积年费用最小法计算不同参数配合下的经济供电半径，如表6和表7所示。

综合表6和表7的计算结果，可得不同负荷密度供电区域下的供电距离，如表8所示。

3.2.2基于电压损失的供电半径计算结果

计算获得满足电压损失的各类供电区域供电半径范围，如表9所示。

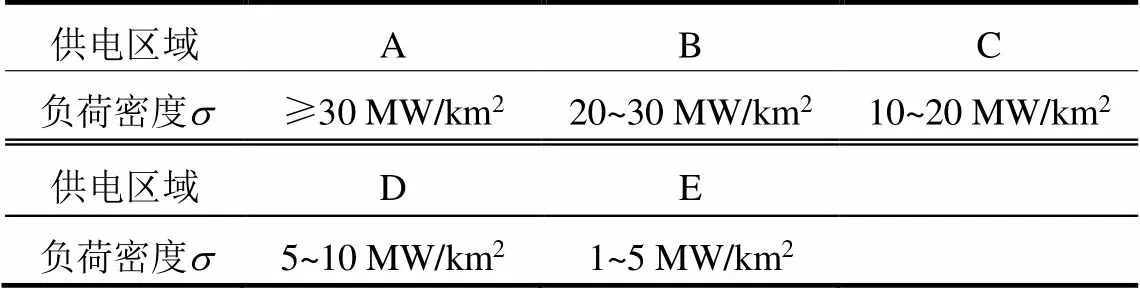
表5 供电区域负荷密度

表6 经济供电半径高值

注：表中变电站为GIS变电站，线路为架空线LGJ-150。

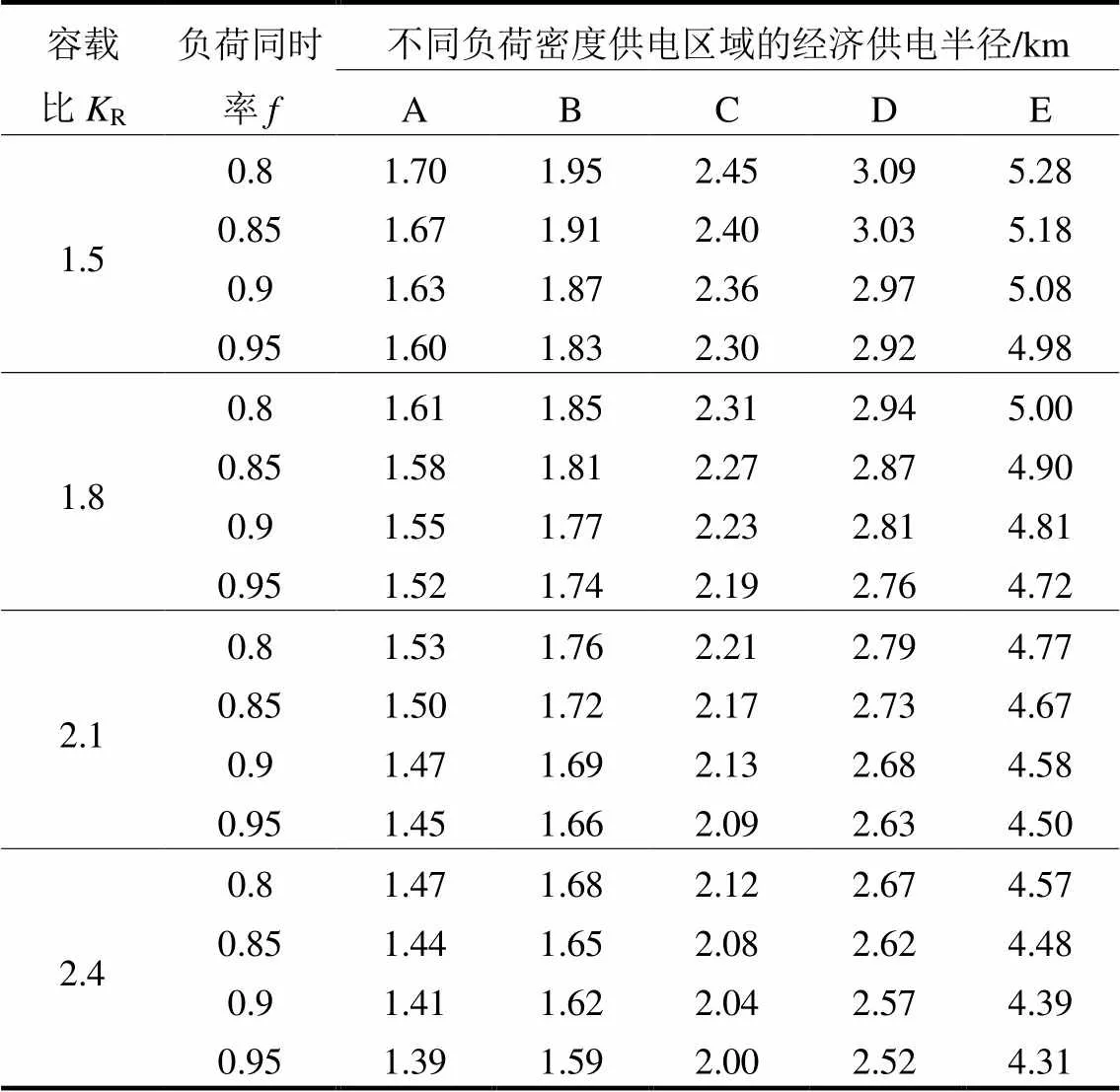
表7 经济供电半径低值

注：表中变电站为常规变电站，线路为电缆YJV-240。

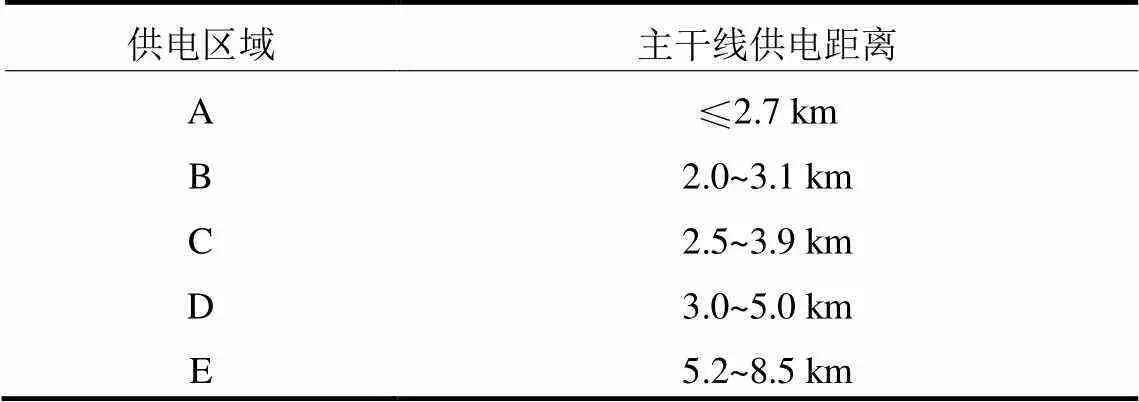
表8 不同负荷密度供电区域的供电距离

注：负荷同时率为0.8～0.95；容载比R为1.5～2.4；最大负荷利用小时数为3000～6000 h；线路曲折系数为1.3。

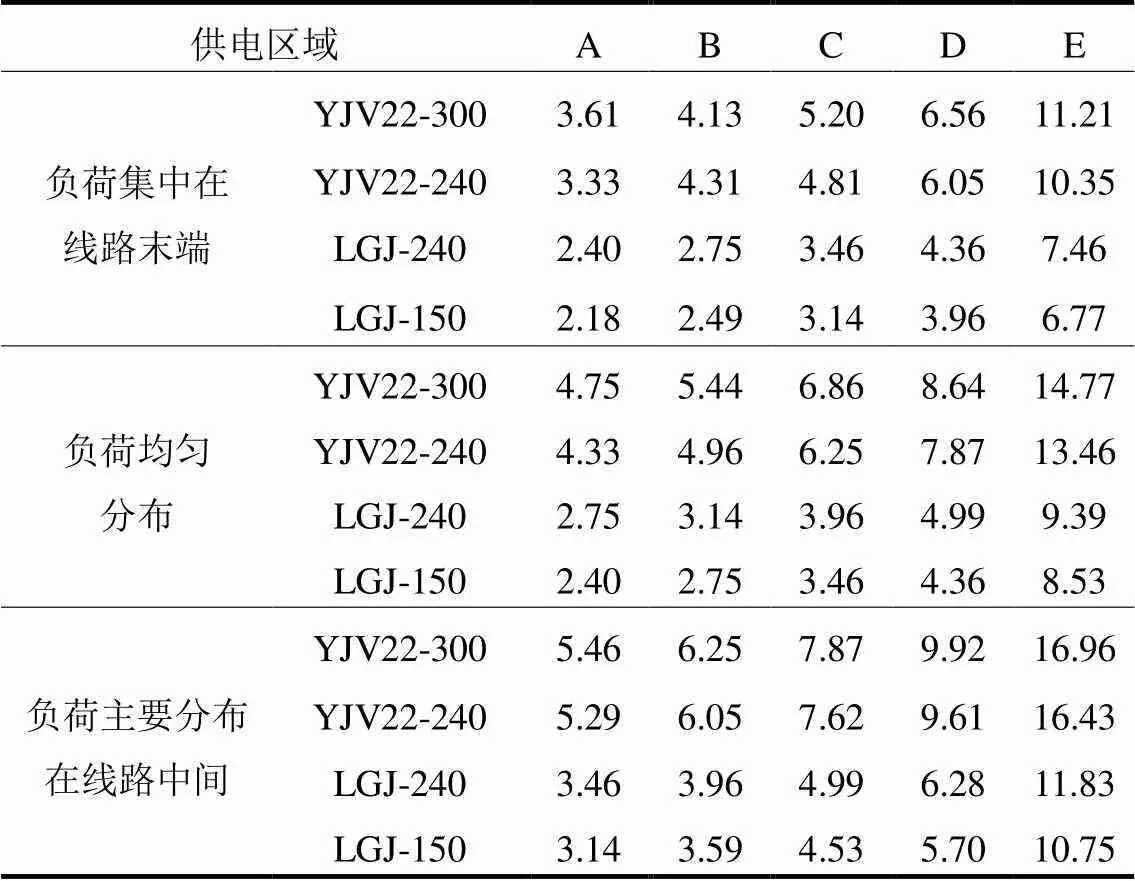
表9 电压损失法测算供电半径(≤km)

注：考虑变电站出线回数在20～48范围内。

3.2.3综合结果

结合以上分析结果，综合考虑单位面积年费用最小，并满足供电半径内电压损失的要求，得到不同负荷密度下各类供电区域的供电半径推荐值，如表10所示。

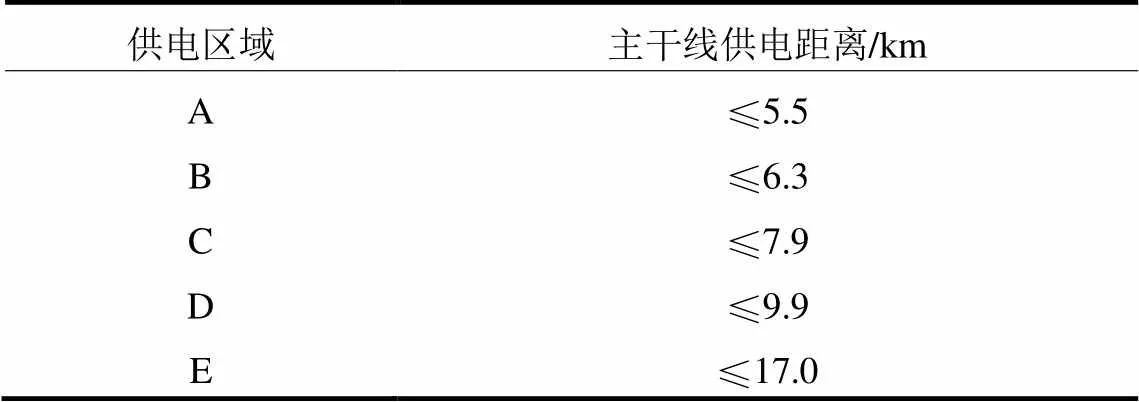
表10 不同类别供电区下供电半径推荐值

注：负荷同时率为0.8～0.95；容载比R为1.5～2.4；最大负荷利用小时数为3000～6000 h；线路曲折系数为1.3。

4  结论

本文综合考虑配电网变电站的变压器和线路的建设及运行参数，建立以单位供电面积年费用最小为目标函数的变电站供电半径优化模型，计及线路沿线电压损失约束，以保证电能质量。所建立的优化模型全面分析不同负荷密度、不同负荷构成和不同负荷分布对变电站供电半径的影响，获得涵盖各类规划运行情况的配电网经济供电半径。所提出的变电站经济供电半径优化模型和求解算法能指导地区配电网规划工作，提高地区配电网规划方案的经济性和可行性。

本文的研究基于常规中低压配电网规划，优化模型和算法中并未计及分布式电源和新型负荷，未来将进一步研究分布式电源和新型负荷接入对变电站经济供电半径的影响。

[1] 唐俊熙, 王梓耀, 张俊潇, 等. 基于文化蚁群算法的高可靠多电源配电网规划模型[J]. 电力系统保护与控制, 2020, 48(7): 99-107.

TANG Junxi, WANG Ziyao, ZHANG Junxiao, et al. High reliability multi-power distribution network planning model based on memetic ant colony algorithm[J]. Power System Protection and Control, 2020, 48(7): 99-107.

[2] 韩俊, 谢珍建, 黄河, 等. 基于停电损失计算与成本分析的配电网单元制供电网格可靠性规划[J]. 智慧电力, 2020, 48(1): 63-68, 117.

HAN Jun, XIE Zhenjian, HUANG He, et al. Unit mesh reliability planning for distribution network based on outage cost calculation and cost analysis[J]. Smart Power, 2020, 48(1): 63-68, 117.

[3] 邵华, 贺春光, 安佳坤, 等. 基于线性约束的有源配电网规划研究[J]. 电力科学与技术学报, 2020, 35(5): 66-74.

SHAO Hua, HE Chunguang, AN Jiakun, et al. Active distribution network planning model based on linearized constraints[J]. Journal of Electric Power Science and Technology, 2020, 35(5): 66-74.

[4] 宁超, 张峰, 李卫华, 等. 基于空间负荷布局的低碳主动配电网扩展规划研究[J]. 电网与清洁能源, 2020, 36(9): 37-42.

NING Chao, ZHANG Feng, LI Weihua, et al. Research on expansion planning of low carbon active distribution network based on space load layout[J]. Power System and Clean Energy, 2020, 36(9): 37-42.

[5] 林卓琼, 彭显刚. 基于帕累托最优法的中低压配电网多属性规划方案比选方法[J]. 广东电力, 2020, 33(8): 46-53.

LIN Zhuoqiong, PENG Xiangang. Comparison method of multi-attribute planning for medium and low voltage distribution network based on Pareto optimality[J]. Guangdong Electric Power, 2020, 33(8): 46-53.

[6] 柳占杰, 许跃进. 基于电压制式的电网最优供电半径研究[J]. 电力系统保护与控制, 2010, 38(19): 87-101.

LIU Zhanjie, XU Yuejin. Research on the optimal grid radius based on standard voltage[J]. Power System Protection and Control, 2010, 38(19): 87-101.

[7] 贾利, 刘令富, 张宇星, 等. 基于负荷密度的配电电压供电距离研究[J]. 中国电力教育, 2008(增刊3): 557-559.

JIA Li, LIU Lingfu, ZHANG Yuxing, et al. Research on power supply distance of distribution voltage based on load density[J]. China Electric Power Education, 2008(S3): 557-559.

[8] 王吉合. 关于配电线路最佳供电半径的探讨[J]. 青海电力, 1999(1): 1-6.

WANG Jihe. On the optimal supply radius of the electrical power distribution system[J]. Qinghai Electric Power, 1999(1): 1-6.

[9] 马永飞, 王沧海. 浅析配电网供电半径与最大负荷的关系[J]. 青海电力, 2011, 30(1): 1-3.

MA Yongfei, WANG Canghai. Discussion the relationship between power supply radius and maximum power supply load of distribution network[J]. Qinghai Electric Power, 2011, 30(1): 1-3.

[10] 郑博文, 李姝润, 杨隽, 等. 配电网规划决策中的可计算性问题研究[J]. 电力系统保护与控制, 2017, 45(22): 16-21.

ZHENG Bowen, LI Shurun, YANG Jun, et al. Study on computable problems in distribution network planning decision[J]. Power System Protection and Control, 2017, 45(22): 16-21.

[11] 顾雨嘉, 许跃进, 尹志. 农村电网优化电压制式及经济供电半径的研究[J]. 农业工程学报, 2010, 26(2): 146-150.

GU Yujia, XU Yuejin, YIN Zhi. Research on optimized voltage pattern and economic power supply radius of rural grid[J]. Transactions of CSAE, 2010, 26(2): 146-150.

[12] 刘友强, 李欣然. 变电站经济容量和经济供电半径的探讨[J]. 广东电力, 2005, 18(11): 7-11.

LIU Youqiang, LI Xinran. Discussion on economical capacity and economical power supply radius for transformer substations[J]. Guangdong Electric Power, 2005, 18(11): 7-11.

[13] 王波, 虞殷树, 贺旭, 等. 计及分布式电源并网安全约束的配电网改接优化模型[J]. 电力系统保护与控制, 2019, 47(22): 67-77.

WANG Bo, YU Yinshu, HE Xu, et al. An optimization model for restructuring distribution network considering grid-connected security constraints of DGs[J]. Power System Protection and Control, 2019, 47(22): 67-77.

[14] 王璞, 王承民, 张焰, 等. 城市配电网规划中变电站最佳供电半径及容量的实用计算方法[J]. 电气应用, 2011, 30(23): 38-41.

[15] 厉达, 程浩忠, 俞国勤, 等. 变电站的经济容量优化模型及其不同负荷密度下的变压器配置研究[J]. 电力系统保护与控制, 2009, 37(19): 5-9.

LI Da, CHENG Haozhong, YU Guoqin, et al. Optimum model for substation’s economical capacity and the configuration of transformer under different load density[J]. Power System Protection and Control, 2009, 37(19): 5-9.

[16] 葛少云, 贾鸥莎. 配电变电站多阶段优化规划模型[J].电网技术, 2012, 36(10): 113-118.

GE Shaoyun, JIA Ousha. Multi-stage model for optimal distribution substation planning[J]. Power System Technology, 2012, 36(10): 113-118.

[17] 张漫, 王主丁, 王敬宇, 等. 计及发展不确定性的配电网柔性规划方法[J]．电力系统自动化, 2019, 43(13): 114-123, 168.

ZHANG Man, WANG Zhuding, WANG Jingyu, et al. Flexible planning methods for distribution network with uncertainties during development[J]. Automation of Electric Power Systems, 2019, 43(13): 114-123, 168.

[18] 曹昉, 孟琦斌, 苗培青, 等. 基于改进加权Voronoi图和遗传算法的变电站规划[J]. 电网技术, 2015, 39(2): 511-516.

CAO Fang, MENG Qibin, MIAO Peiqing, et al. Optimal substation planning based on improved weighted Voronoi diagram and Genetic algorithm[J]. Power System Technology, 2015, 39(2): 511-516.

[19] 胡玉生, 瞿进乾, 张辉, 等. 变电站规划优化解析模型和简化算法[J]. 智慧电力, 2018, 46(1): 63-70.

HU Yusheng, QU Jinqian, ZHANG Hui, et al. Analytical models and simplified algorithms for substation optimization planning[J]. Smart Power, 2018, 46(1): 63-70.

[20] HE Yuqing, CHEN Yuehui, YANG Zhiqiang. A review on the influence of intelligent power consumption technologies on the utilization rate of distribution network equipment[J]. Protection and Control of Modern Power Systems, 2018, 3(2): 183-193.

[21] MAZHARI S M, MONSEF H, ROMERO R. A hybrid heuristic and evolutionary algorithm for distribution substation planning[J]. IEEE Systems Journal, 2015, 9(4): 1396-1408.

[22] RAVADANEGH S N, ROSHANAGH R G. On optimal multistage electric power distribution networks expansion planning[J]. International Journal of Electrical Power & Energy Systems, 2014, 54: 487-497.

[23] RAVADANEGH S N, ROSHANAGH R G. A heuristic algorithm for optimal multistage sizing, siting and timing of MV distribution substations[J]. Electric Power Systems Research, 2013, 105: 134-141.

[24] 郑爽, 杨晓楠, 句荣滨, 等. 两种启发式电网规划算法的比较与改进[J]. 电力系统保护与控制, 2019, 47(17): 109-116.

ZHENG Shuang, YANG Xiaonan, JU Rongbin, et al. Comparison and improvement of two heuristic algorithms for power network planning[J]. Power System Protection and Control, 2019, 47(17): 109-116.

[25] 刘旭娜, 魏俊, 张文涛, 等. 基于信息熵和模糊分析法的配电网投资效益评估及决策[J]. 电力系统保护与控制, 2019, 47(12): 48-56.

LIU Xuna, WEI Jun, ZHANG Wentao, et al. Investment benefits evaluation and decision for distribution network based on information entropy and fuzzy analysis method[J]. Power System Protection and Control, 2019, 47(12): 48-56.

[26] 孔祥玉, 尧静涛, 崔凯, 等. 考虑分布式电源接入的区域配电网规划投资决策方法[J]. 中国电力, 2020, 53(4): 41-48.

KONG Xiangyu, YAO Jingtao, CUI Kai, et al. Investment decision-making method for regional distribution network planning considering distributed generations[J]. Electric Power, 2020, 53(4): 41-48.

[27] 纪雯. 电力系统设计手册[M]. 北京: 中国电力出版社, 1998.

[28] 赵俊光, 王主丁, 乐欢. 中压配电网规划中馈线电气计算的估算方法[J]．电力系统自动化, 2008, 32(16): 98-101.

ZHAO Junguang, WANG Zhuding, YUE Huan. Estimation method for electrical calculation of feeders in middle voltage distribution network planning[J]. Automation of Electric Power Systems, 2008, 32(16): 98-101.

[29] 方向晖. 中低压配电网规划与设计基础[M]. 北京: 中国水利水电出版社, 2004.

Economic power supply radius of a substation in a distribution network

CHENG Junzhao1, LI Fangfang1, MO Haifeng1, XU Min2, YUAN Zhiyong2

(1. Power Grid Planning and Construction Research Center, Yunnan Power Grid Co., Ltd., Kunming 650011, China; 2. Electric Power Research Institute, CSG, Guangzhou 510080, China)

To lower cost and improve power supply quality, the economic power supply radius of a substation is investigated. First, taking the construction cost as well as operation and maintenance cost into consideration, an economic power supply optimization model of the substation to minimize the annual supply cost of per unit area is established and a solution method is provided. Then, the quantitative relationship between power supply radius and voltage loss of lines under different load scenarios is also established, through which the voltage quality of optimized economical power supply radius is examined according to voltage loss regulation in the distribution network. The correctness and effectiveness of the proposed method are verified using actual distribution network data. The result provided can be used as a reference in regional distribution network planning.

distribution network; substation; planning; economic power supply radius; line voltage loss

10.19783/j.cnki.pspc.201598

2020-12-23；

2021-06-28

程军照(1982—)，男，硕士，高级工程师，研究方向为配电网规划；E-mail: chengjunzhao@126.com

李芳方(1987—)，男，本科，高级工程师，研究方向为配电网规划。E-mail: 407514199@qq.com

南方电网公司重点科技项目“基于数据深度分析的配电网精准规划投资决策技术研究”(059100KK52190009)

This work is supported by the Key Science and Technology Project of China Southern Power Grid Co., Ltd. (No. 059100KK52190009).

(编辑 魏小丽)