基于ADINA的水利枢纽闸门预应力结构参数设计优化研究

刘忠干

(广东省源天工程有限公司，广州 511340)

1 概述

水工结构设计水平关乎水利设施的运营可靠性，而此安全问题不仅仅是静力场应力、位移稳定性，同样也与结构抗震设计密切相关[1-2]，有效结合静、动力场安全综合技术优势，才更利于水工设计优化。宋峰[3]、许涛等[4]、李艺等[5]从结构静力场计算考虑，采用ANSYS等数值计算方法，分析了不同设计方案下闸门、挡墙等水工建筑的应力、位移变化特征，由此评价结构最优设计方案。何志亚等[6-7]、沈卫[8]从水工建筑渗流场特征参数影响效应评价，利用模型试验方法开展了消能池、溢洪道等水利设施的体型优化，丰富了水工设计优化成果。地震动响应特征研究可以依赖于振动台试验或地震动仿真计算，杨玉生等[9]、冯新等[10]采用前一种试验方法，开展了水工设施的地震动响应特征分析，有助于揭示结构抗震设计机理。杨庚鑫等[11]、曹洋等[12]采用地震动拟静力法、振型分解或反应谱叠加等方法，开展了水工结构的地震动响应特征分析，有助于探讨不同方案下动力响应特征，推动水工设计优化与地震动力响应特征的联系性。本文根据扩建水利枢纽预应力结构体系与闸门钢梁结构的设计优化问题，针对结构拉锚系数参数开展静、动力场综合计算评价，为该闸门钢结构安全设计提供参考。

2 模拟设计分析

2.1 工程概况

北江作为粤北地区重要地表供水来源，有效的供水枢纽对提升地区用水安全具有重要意义，特别是水工设施安全运营与之密切相关，对解决地区水资源分布时空离散具有重要作用。在北江原水利枢纽基础上考虑进行扩建，重点在泄洪闸、溢洪道及输水灌渠等水利设施上，计划扩建后水利枢纽工程可实现年最大供水量超过1 200万m3。北江水利枢纽溢洪道位于泄洪闸右坝段，平面布置如图1所示，整体支撑加固体系采用预应力锚索。根据工程扩建设计，计划泄洪闸采用多孔式闸门通流设计形态，其底板厚度为1.2 m，闸室轴线全长为8 m，单孔净宽为3.5 m，以弧形钢闸门为挡水设施，根据设计部门的初步设计，其模型如图2所示，闸门全面板上最大压强可支持达 1.5 MPa。泄洪水闸整体支撑结构为8根预应力混凝土闸墩，墩径为1.2 m，其立面分布如图3所示。由于泄洪闸作为该扩建水利枢纽的重要水工建筑，特别是其闸门导流设施，有效的支撑加固设计对提升整体运营具有较大帮助，因而工程管理部门综合泄洪闸与溢洪道两水工建筑的预应力体系，讨论以泄洪闸门推力与支撑结构体系的预应力为研究对象，评价此两“力”的比值参数拉锚系数最优化设计。

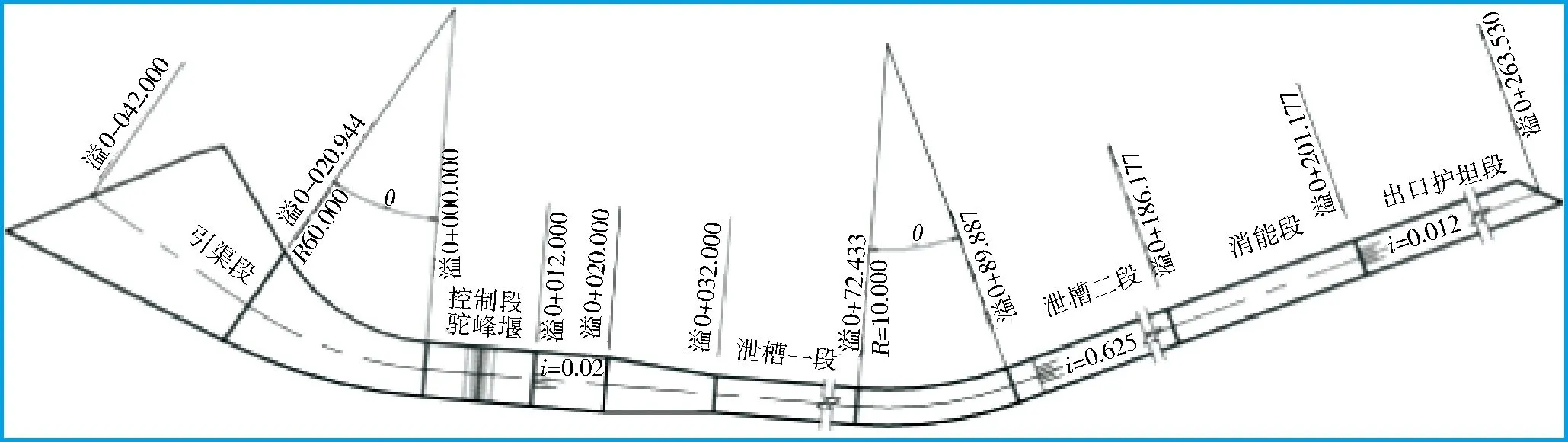
图1 溢洪道平面示意

图2 闸门模型示意

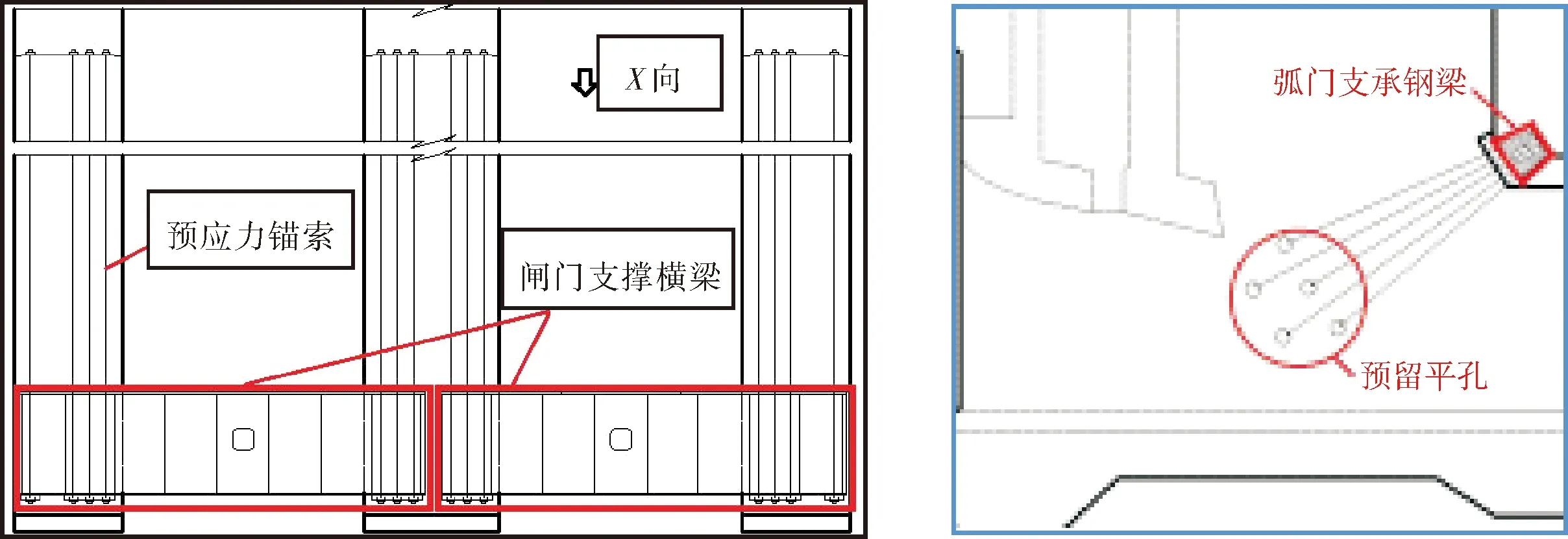
a 闸门与横梁立面 b 闸门与钢梁结构剖面

2.2 设计模拟

根据对泄洪闸门结构分析，其支撑加固钢结构剖面如图4a所示，对称式分布有两边梁，并与预应力锚索相耦接，全轴线长度为5 m，采用型钢构件，其跨中处设置有集中垫板，避免荷载传递偏心，上、下翼缘厚度分别为60 mm、45 mm，加劲肋板厚度为40 mm，肋间距为2.6 m。采用的腹板为耐拉材料，厚度为30 mm。为确保优化设计计算结果可靠性，本文在前期综合对比基础上，设定钢梁结构翼缘宽厚比与腹板高厚比参数分别为30、56，腹板与闸门向夹角为82°，钢梁结构立面如图4b所示。

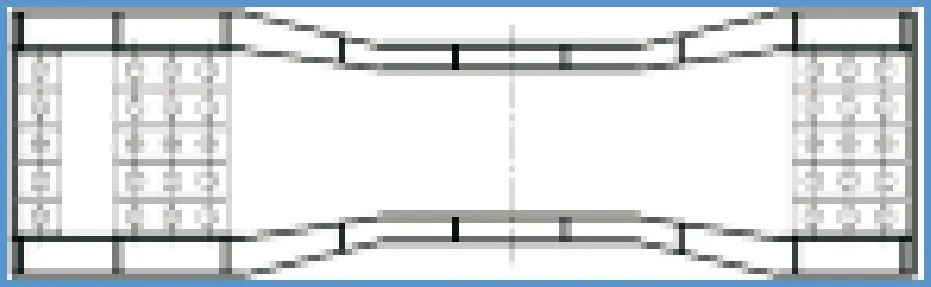
a 钢结构剖面

采用CAD几何建模与ADINA仿真计算相结合方式[13-14]，建立该泄洪闸整体模型及钢结构计算模型(如图5所示)。整体泄洪闸模型中均采用与闸身主材相匹配的力学本构模型，变形方程与物理力学参数均来自工程实测，共获得网格为168 284个，节点数为145 832个。该钢梁结构计算模型中顶、底面分别设定为法向单一约束与全向约束边界条件，计算闸上、下水位按照运营期设定。模型中X～Z正向分别取顺闸墩流水向、闸室右岸方向及结构重心上方。

a 整体模型

由于拉锚系数在已知工程中分布区间较广，结合本工程具体现状及国内已应用工程[15-16]，拉锚系数最大未超过3.5，本文在整体结构其他设计参数均为一致的前提下，仅改变拉锚系数，且固定设定单支锚索张拉荷载为4 650 kN，确定拉锚系数分布在1～3，且对比方案按照梯次0.3设定，共有8个方案。由于本文需优化设计的为一个比例参数，且该比例参数牵涉面包括有闸门与预应力锚索，因而需综合有效评判最优参数影响的静、动力响应特征。静力响应特征涉及外荷载主要以结构自重及水压力为主，而地震动荷载采用与本工程场地相匹配的峰值加速度地震动参数，为多频率峰值加速度的EI Centro地震波，其0～8 s内的加速度时程谱如图6所示。地震动响应计算过程中设定模型具有粘滞性边界条件，并采用拟静力法将加速度时程分布输入至模型动荷载中，综合静、动力对比计算，分析上述8种拉锚系数设计方案的优劣。

图6 加速度时程谱示意

3 结构静力影响特征

3.1 应力特征

根据对结构静力场计算，获得了不同拉锚系数方案下结构拉应力影响特征(如图7所示)。分析图7中拉应变变化可知，受拉锚系数变化，各处拉应力均有差异性变化特征，其中下翼缘与腹板拉应力具有一致性类似特征，随拉锚系数增大，两处拉应力均为先减后增变化，以拉锚系数2.2方案下拉应力为最低，分别为3.02 MPa、2.1 MPa，而下翼缘在拉锚系数1、1.6方案内拉应力较前者分别增大了124.1%、53.6%，而拉锚系数2.2拉应力最低方案较之拉锚系数2.5、3.1下分别减少了9.3%、43.1%；整体上看，在梯次0.3增长的拉锚系数1～2.2方案内，下翼缘与腹板拉应分别具有平均降幅18.1%、20%，而超过节点方案后，两处拉应力的增幅分别为21%、25.8%。从结构抗拉安全性考虑，在拉锚系数低于2.2时更利于此两处安全。加劲肋处拉应力随拉锚系数为递减变化，在拉锚系数低于2.5方案前，其拉应力为结构上最高，但在该方案后，其拉应力甚至接近腹板处量值。从拉应力的降幅来看，集中在拉锚系数1～2.2方案阶段内，该梯次区间内最大降幅达22.7%，平均降幅为21.4%，而拉锚系数超过2.2后，加劲肋拉应力最大降幅仅为1.5%。从加劲肋处拉应力影响与设计优化考虑，控制拉锚系数位于较合理区间更佳。上翼缘处拉应力与前三处有所差异，其在拉锚系数1～2.2区间方案内，拉应力稳定在1.5MPa左右，最大变幅不超过2%，而拉锚系数为2.5、3.1后，其拉应力较前阶段稳定值分别增长了22.8%、101.1%，因而确保上翼缘安全稳定性与拉锚系数位于1～2.2密不可分。综合拉应力影响变化来看，各处拉应力均在拉锚系数 1～2.2方案内表现更优，而从优化设计考量，拉应力的最优方案应为拉锚系数2.2。

图7 拉应力与拉锚系数参数关系示意

图8为拉锚系数2.2方案下预应力闸墩结构与弧门面板预留孔第一主应力分布特征。从图8中可知：预应力闸墩与弧形闸门的接触面上最大主应力为1.9 MPa，位于预应力锚索与加固钢梁的凹面处，整体预应力闸墩受拉应力不超过1 MPa。锚索预留孔中由于应力集中效应，其拉应力较大，达3.3 MPa，此与钢梁结构与预应力闸墩间的垫块接触位置有关。整体上看，在该拉锚系数方案下，钢结构拉应力满足设计安全要求。

a 钢梁接触面

3.2 位移特征

同理，可获得加固结构位移特征(如图9所示)，包括有结构各向位移与钢结构截面跨中与端部处挠度变化。从图9中可知，三向位移与拉锚系数关系均保持一致，以拉锚系数2.2方案下位移值最低，X～Z三向位移分别为4.5 mm、4.97 mm、5.84 mm。当拉锚系数低于2.2时，拉锚系数愈大，对结构各向位移具有抑制效应，当拉锚系数方案内梯次增长0.3，则X～Z向位移分别平均可减少18.1%、19.1%、18.4%，而拉锚系数超过2.2后，拉锚系数对结构变形具有促进作用，不利于结构安全稳定，X～Z各向位移在该梯次区间内分别具有平均增幅25.1%、25.6%、26.3%。在三向位移影响表现过程中，以拉锚系数2.2方案下更利于结构静力场稳定性。

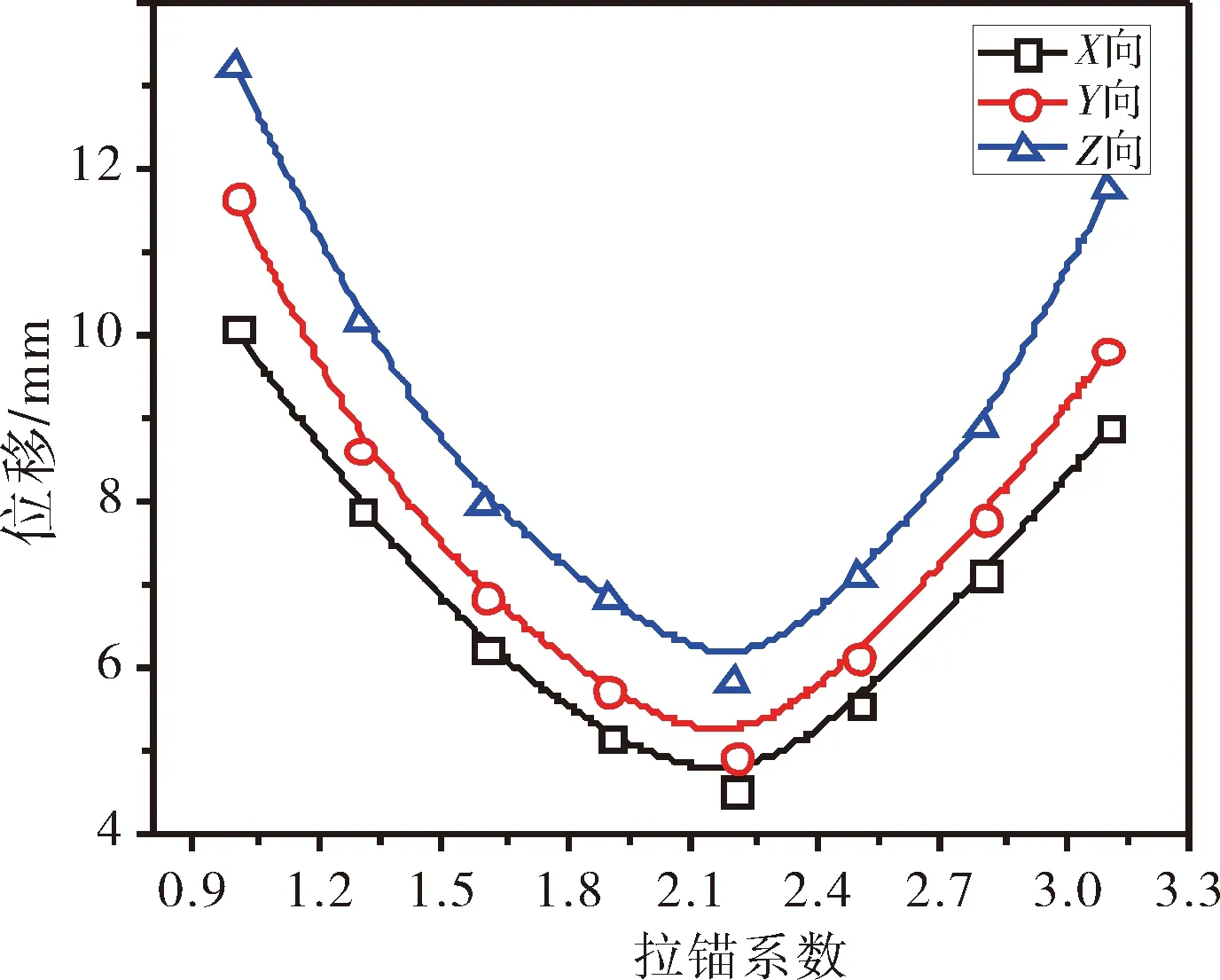
a 各向位移

从钢结构截面跨中与端部挠度来看，两者挠度值与拉锚系数具有差异性，端部挠度随拉锚系数的变化特征与结构各向位移变化一致，以拉锚系数2.2方案下为最低，达2.3 mm，但在该方案后，端部挠度出现较大增幅，甚至量值超过跨中挠度；而跨中挠度在拉锚系数增长过程中均保持递减，只是在拉锚系数维持在低于2.2时集中较大增幅，其中拉锚系数2.2方案下挠度较之系数1.3、1.9下分别减少了38.3%、12%，而在拉锚系数2.2方案后挠度低于端部，其挠度值过渡至稳定状态。结合各向位移与截面挠度变化可知，不论是位移限制亦或是挠度控制，在拉锚系数2.2下结构静力场更处于设计最优。

4 结构动力响应特征

基于EI Centro地震波的叠加计算，获得不同拉锚系数的方案下，闸门加固钢结构跨中处加速度响应特征(如图10所示)。

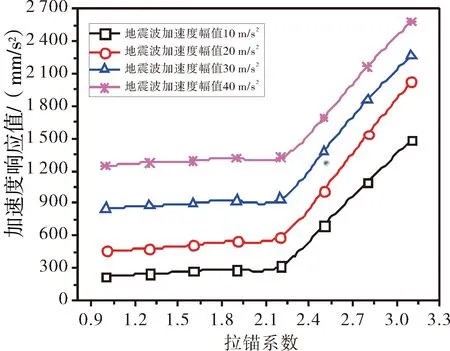
图10 加速度响应特征示意

从图10中可知，EI Centro地震波峰值加速度愈大，则结构地震动响应特征值愈高，在拉锚系数1.3方案下，EI Centro波的峰值加速度10 m/s2工况下加速度响应值为249.1 mm/s2，而动荷载峰值加速度每增大10 m/s2下，其加速度响应值平均可增长73.7%，对结构抗震设防来说难度加大。而拉锚系数增长至1.9、2.2或3.1时，其加速度响应值随地震波峰值加速度幅值的影响增幅分别为61.3%、20.7%，即拉锚系数愈大，受动荷载幅值影响更弱[17]。同一幅值地震波下拉锚系数愈大，则加速度响应值水平愈大，但在4个地震波幅值工况中，加速度响应值随拉锚系数的变化可分为两阶段特征：在拉锚系数1～2.2方案内，加速度响应值水平增幅较小，地震波幅值10～40 m/s2下梯次拉锚系数增长过程中分别具有平均增幅9.2%、6.7%、2.4%、1.5%；而在系数为2.2～3.1方案内，其加速度响应值增幅较为显著，4个工况中平均增幅分别超过了70.2%、51.1%、34.5%、25.3%，极不利于结构抗震设计，因而从拉锚系数控制结构动力响应角度考虑，静力场设计优化的2.2方案亦利于结构抗震要求。

5 结语

1) 下翼缘与腹板拉应力随拉锚系数均为先减后增变化，以拉锚系数2.2方案下最低，分别为3.02 MPa、2.1 MPa；加劲肋处拉应力随拉锚系数为递减变化，但降幅在拉锚系数1～2.2方案内，最大降幅达22.7%；上翼缘处拉应力在拉锚系数1～2.2方案内稳定在1.5 MPa，超出该方案区间为递增态势；拉锚系数2.2方案下主应力分布较合理，主应力值满足安全要求。

2)X～Z向位移均以拉锚系数2.2方案下位移值最低，分别为4.5 mm、4.97 mm、5.84 mm；在拉锚系数低于2.2时，各向位移处于抑制，而超过该值后，作用相反；端部挠度以拉锚系数2.2方案下为最低，而拉锚系数超过该方案后，挠度具有较大增幅，跨中挠度在拉锚系数低于2.2方案内具有较大降幅，但在系数2.2方案后降幅趋稳定。

3) 地震波幅值愈大，则结构加速度响应值愈高，且拉锚系数愈大，加速度响应值受地震波幅值影响影响愈小；拉锚系数愈大，加速度响应值愈大，但增幅具有两阶段特征，拉锚系数1～2.2方案内，地震波幅值10～40 m/s2下分别具有平均增幅9.2%、6.7%、2.4%、1.5%；而在系数为2.2～3.1方案内，平均增幅分别超过了70.2%、51.1%、34.5%、25.3%。

4) 综合结构静、动力场影响特征，拉锚系数2.2下结构静力安全与动力场抗震设计均最优。