弹性接触支撑梁横向振动动力学建模研究

陈校锋，朱 翔，李天匀，毛艺达，王春旭

（1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.船舶与海洋水动力湖北省重点实验室，武汉 430074；4.中国舰船研究设计中心，武汉 430064）

梁结构在工程中得到广泛使用，其振动中的非线性通常包括物理非线性、几何非线性和边界条件的非线性。对于船舶推进轴系等梁类结构的振动，激振测试表明轴系与船体结构的横向振动具有强耦合特性，且是接触耦合，这种接触耦合一般是非线性的。关于物理或几何非线性梁的振动已经受到众多学者的关注。Pielorz[1]分析了悬臂梁在小应变下的大挠度和大转动时的有限振动，采用伽辽金法求解弹性和黏弹性梁的双曲或抛物非线性偏微分方程。Barari 等[2]采用变分迭代和参数摄动法研究了轴向载荷作用下Euler-Bernoulli梁的非线性振动，将结果和误差与四阶Runge-Kutta 法的计算结果进行了比较。刘小靖等[3]提出了一种修正小波伽辽金法，用以解决任意强非线性的梁弯曲问题，该方法克服了边界延拓问题，成功用于求解具有非线性特征的梁的大挠度弯曲问题。贾布裕等[4]考虑了材料的弹塑非线性对计算组合梁的可靠度的影响，结果表明几何非线性降低了组合梁结构的可靠度值。祖福兴等[5]将配点法与径向基函数相结合，得到了一种适用于求解非线性梁的计算方法。黄正等[6]借助向量式力学的思想，提出了一种新的有限质点法来描述梁的非线性变形。张年梅等[7]研究了受轴向载荷作用的非线性弹性梁的混沌运动，采用Melnikov 法确定系统发生混沌的临界条件。

典型的边界条件非线性包括结构构件间的接触或间隙，各构件间的相互碰撞、分离及摩擦容易引发机械振动和噪声，导致系统性能下降等一系列问题[8]。目前，已有部分学者针对接触或间隙边界条件下非线性梁的振动问题开展了相关的研究。Turner[9]采用多尺度法研究了赫兹接触边界条件下悬臂梁的非线性振动问题，通过推导证明了非线性幅频关系取决于模态数和线性接触刚度。Sedighi等[10－11]针对死区非线性问题，提出了一种新的有效的精确等效函数，并采用参数展开法研究了存在死区非线性边界条件悬臂梁的非线性振动。翟国富等[12]对含有非线性赫兹接触条件的双梁结构进行了冲击特性分析，其结果相比于线性模型更能准确地预测接触系统的耐冲击能力。相关学者也进行了试验研究，Praveen 等[13]从实验和数值两方面研究了悬臂梁双侧碰撞的振动问题，考虑了接触刚度、间隙和接触材料对结果的影响。曹妍妍等[14]同样以具有间隙约束的悬臂梁为试验模型，分析了系统在不同激励参数和接触刚度下响应状态随系统参数的变化规律。万雨婷等[15]采用扫频的方式研究了含间隙限位约束梁结构的一阶频响特征，考虑了激励幅值和间隙大小对结构振动特性的影响。

从以上研究可见，针对梁与弹性支撑在接触状态下的研究还相当匮乏，相关研究尚难以揭示梁和弹性支撑在接触状态下的非线性动力学特性。本文将弹性梁与支撑弹簧的非线性接触简化为用一种分段线性模型表示，通过能量法建立三支撑弹性接触梁的动力学模型，采用Runge-Kutta法分析模型在简谐激励下的动态特性，并讨论了激励参数和支撑刚度对结构非线性振动特性的影响。

1 弹性接触支撑梁横向振动动力学模型

考虑三支撑弹性接触梁模型，模型中假设支撑弹簧只能压缩而不能伸长，以此来模拟梁和支撑弹簧的接触行为，如图1所示。以弹性梁的左端面作为x轴的原点，梁刚接触弹簧即弹簧无压缩时的位置为初始位置和z轴的原点。梁的长度为l，横截面宽为b，厚为h。材料密度为ρ，杨氏模量为E。支撑弹簧分别位于x1、x2、x3处，其刚度分别为k1、k2、k3。在梁的左端x0处作用垂向动态激励力F。

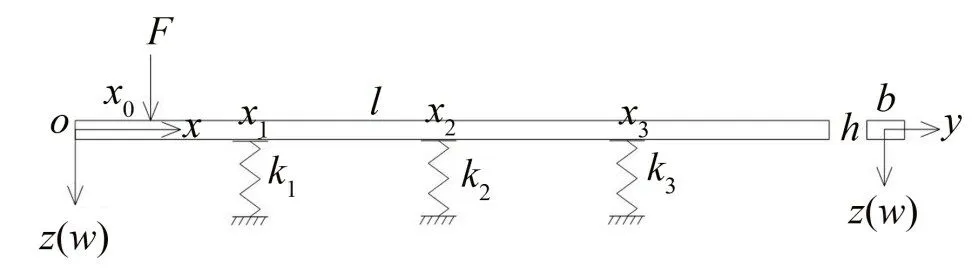
图1 三支撑弹性接触梁模型示意图

为了求解接触支撑梁在受到激励后的响应，采用假定振型法来确定接触支撑梁的运动方程，假设接触支撑梁的横向位移为：

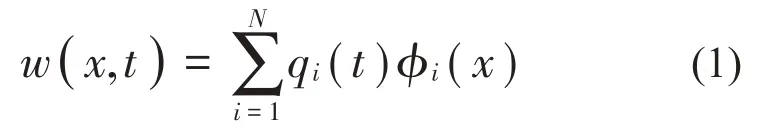
式中的形函数假设为：

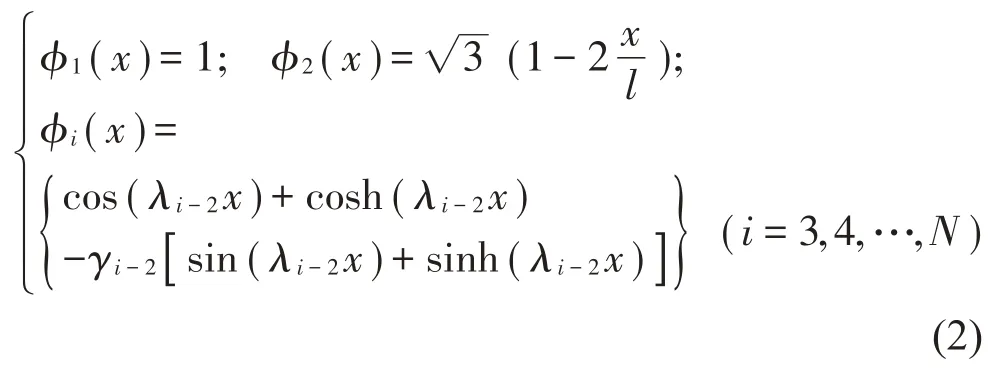
其中：γi-2=且 1-cosλlcoshλl=0，可近似取λi-2=其中形函数的前两项φ1(x)和φ2(x)为两端自由梁运动的刚体模态，描述梁垂向的平动和转动。

假设梁为线弹性材料，则梁的动能和应变能可以分别表示为：

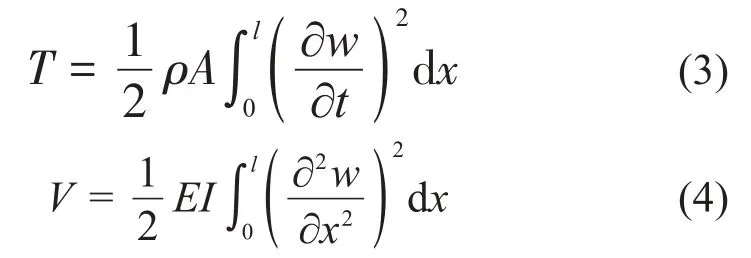
其中：A为横截面面积，I为惯性矩。忽略支撑弹簧的质量，则其弹性势能为：

考虑重力的影响，梁的重力势能为：

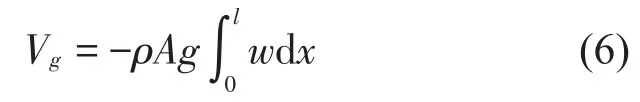
激励力做功：

根据哈密顿原理：

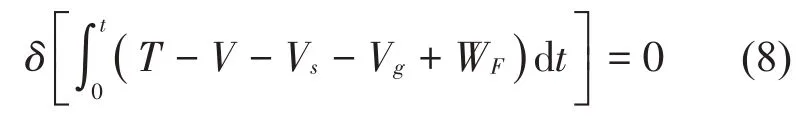
由此得到接触支撑梁的运动方程为：

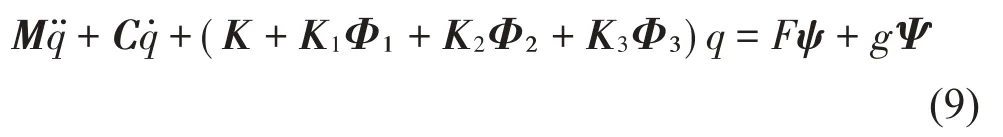
假设系统的阻尼形式为瑞利阻尼，即：

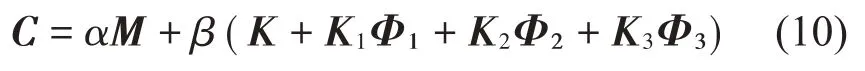
其中：α和β是比例系数，假设弹簧只能压缩，则：

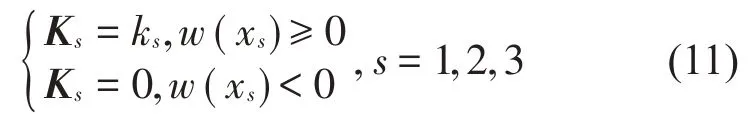
由此可以看出，本文将弹性接触支撑梁的振动等效为一种分段线性振动。

引入2N维状态向量p(t)=，则运动方程可写成1阶微分方程组[16]：

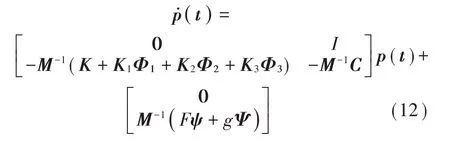
采用经典的4 阶Runge-Kutta 法对q(t) 的值进行求解，再代回假定位移的表达式中，即可得到该时刻梁在任意位置处的横向位移。

当分析模型被简化为线性模型时，支撑弹簧与梁之间不产生分离，此时可以通过改变梁与弹簧的连接条件，即可得到线性弹簧支撑梁模型，可同样采用Runge-Kutta法进行时域响应分析，或者采用能量法进行频域响应分析。

2 算例分析

在算例分析中，取以下参数进行计算：梁的材料密度为ρ=7 850 kg/m3，杨氏模量为E=2.1×1011Pa，梁长l=2 m，宽b=0.05 m，厚h=0.05 m，支撑弹簧的刚度分别为k1=k2=k3=1×106N/m，位置坐标分别为x1=0.5 m，x2=1 m，x3=1.5 m。激励位置坐标x0=0.2 m，重力加速度g=9.8 m/s2。

形函数的截断项数N取10，通过对式(9)的求解，得到弹性支撑梁的前3 阶固有频率分别为30.27 Hz、40.52 Hz、75.52 Hz。

根据下式计算瑞利阻尼的比例系数[17]：

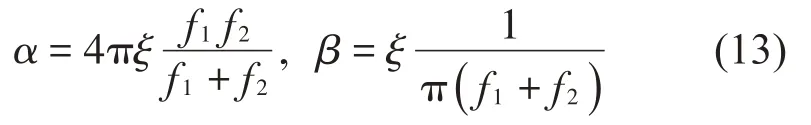
由于主要考虑梁的低频振动，取f1=10 Hz、f2=100 Hz，阻尼比取ξ=0.03，得到α=3.427 s-1，β=8.681×10-5s。

在x0处施加垂向的简谐激励力，激励幅值为150 N，频率为10 Hz，进行时域响应分析，分析时长为t=10 s。接触支撑梁在x1处的响应结果如图2所示，其中图2(c)和图2(d)是根据接触支撑梁在6 s～10 s时间内的位移及速度响应所绘制的相平面图和庞加莱截面图。

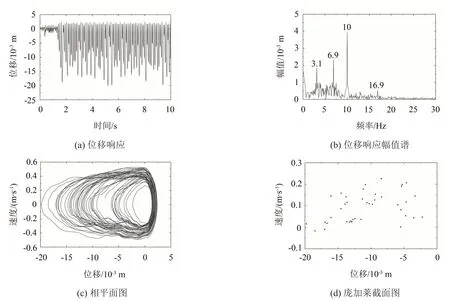
图2 接触支撑梁在简谐激励下的时域响应(F=150 N，f=10 Hz)

计算结果表明，在该激励下的梁和弹簧的接触行为处于接触(u(xs)≥0)与不接触(u(xs)＜0)交替进行的状态。位移响应幅值谱的峰值频率点中并没有出现弹性支撑梁的固有频率点，而是出现了非线性振动中所特有的超谐波共振和次谐波共振。从相平面图和庞加莱截面图则可以更明显地看出接触支撑梁的响应不是简单的周期或准周期运动，而是一种有界的不规则的稳态运动形式，说明弹性接触支撑梁的运动是非线性振动。

3 验证分析

3.1 有限元模型

为了验证本文计算方法的正确性，采用了有限元分析软件ANSYS 对三支撑弹性接触梁进行建模分析。弹性梁采用BEAM188 梁单元模拟。进行模态分析时，不考虑梁与弹簧的接触行为，即支撑梁模型的弹簧采用COMBIN14弹簧单元模拟；进行时域响应分析时考虑接触的情况，即接触支撑梁模型的弹簧采用COMBIN40弹簧单元模拟，该单元的物理模型如图3所示。

图3中的GAP 表示间隙的大小，当u(J)-u(I)+GAP≥0 时，间隙打开，此时弹簧不受力，当u(J)-u(I)+GAP＜0时，间隙闭合，弹簧受压。在本文中，可将GAP设置为一个足够小的小量，用以模拟梁和弹簧的接触行为。设置梁单元的大小并划分网格，约束弹簧下端点处的所有位移，得到接触支撑梁的有限元模型，如图4所示。

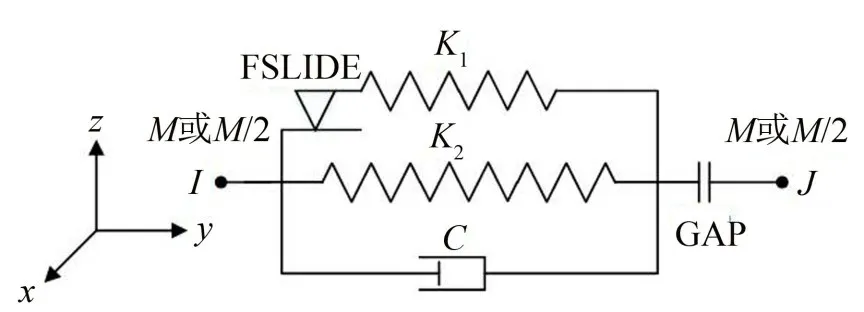
图3 COMBIN40单元

图4 三支撑弹性接触梁有限元模型

3.2 结果对比

当不考虑梁与弹簧的接触行为时，计算弹性支撑梁的固有频率，如表1所示。可以看出，在形函数的截断项数N=10 时，本文的求解结果已经收敛，且前5 阶固有频率与有限元结果的误差均在1.5%以内，说明形函数取N=10进行计算分析是较为准确可靠的。

表1 弹性支撑梁的固有频率/Hz

考虑梁与弹簧的接触行为，对弹性接触支撑梁有限元模型施加激励幅值为150 N，频率为10 Hz的简谐激励，选用Newmark-β直接计算法进行瞬态分析，对比本文和有限元的计算结果，如图5所示。可以看出两种方法的计算结果吻合较好，表明本文所采用的计算方法是可行的，准确的。

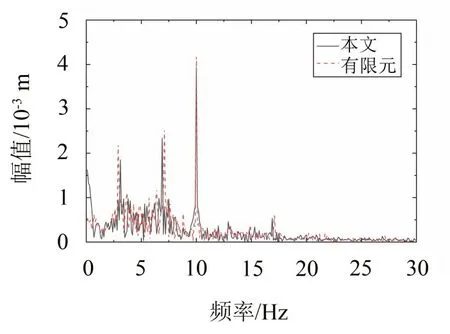
图5 弹性接触支撑梁时域响应结果对比(x1处的位移幅值谱)

4 参数讨论

对于非线性系统，其初始状态对振动的特性有较大影响。尤其是当系统进入混沌后，系统对初始值十分敏感，即初值的微小扰动会使系统的长期运动发生很大变化，其运动是一种有界的不规则的稳态运动[18]。其中有界是指混沌运动的状态变量(如：位移、速度)是在某个区间内变动的，不规则指的是其运动轨迹没有规律可循，类似于随机运动。本节通过分岔图研究弹性接触支撑梁系统中所施加激振力的幅值、频率和弹簧刚度对接触支撑梁运动状态的影响。分岔图是由状态变量和分岔参数所构成的图形空间，表示状态变量随参数的变化。

以接触支撑梁在支撑位置x1处的位移作为状态变量，激励力的幅值作为分岔参数绘制接触支撑梁关于激励幅值的分岔图，如图6所示。其中，激励频率为10 Hz，激励幅值的变化范围是50 N～300 N。在F＜138 N 时，分岔图表现为1 条随激励幅值变化的曲线，表明接触支撑梁在该激励下的运动为周期运动。当F≥138 N时，其运动状态突然改变，进入了混沌运动，在分岔图上表现为一个分岔参数对应无限个状态变量点。运动状态的突然改变可能是因为激励幅值增大到一定的值，梁和弹簧的接触行为一直处于接触与不接触交替进行的状态，从而进入了混沌。而激励幅值小于这个值时，梁和弹簧最终会处于接触的状态，不再分离，此时结构为线性系统，故梁的运动为周期运动。

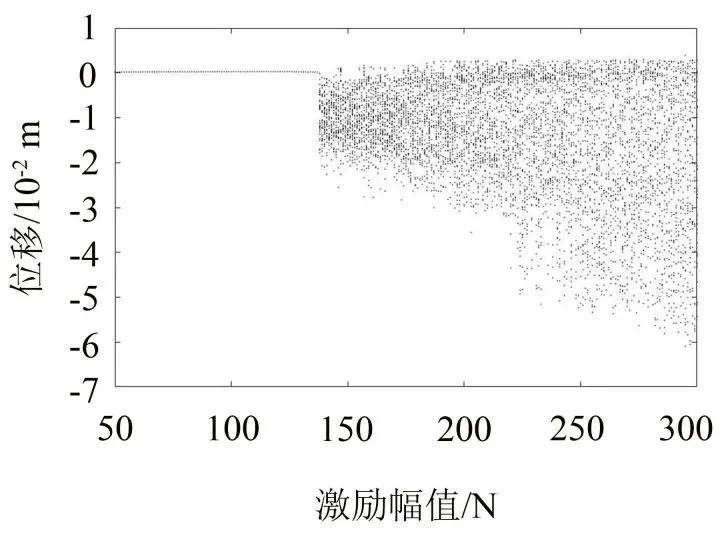
图6 接触支撑梁关于激励幅值的分岔图

固定激励力幅值为200 N，以x1处的位移作为状态变量绘制分岔图，激励的频率范围为10 Hz～100 Hz，如图7所示。分岔图中某个分岔参数下的状态变量为有限个(k个)孤立点，可以表示系统在该分岔参数下的周期k运动[18]。从图7可见，接触支撑梁在激励频率f小于76.5 Hz的大部分区间内均作混沌运动，而在46 Hz～48 Hz 和60 Hz～68 Hz 之间，接触支撑梁分别发生了周期2和周期1运动。最后，接触支撑梁的振动大约在77 Hz处从混沌运动转为周期2运动，并在79.5 Hz处进入周期1运动。此外，随着激励频率的增大，状态变量的变化区间呈现减小的趋势。因此，当激励频率较低时，接触支撑梁的运动更有可能进入混沌运动。

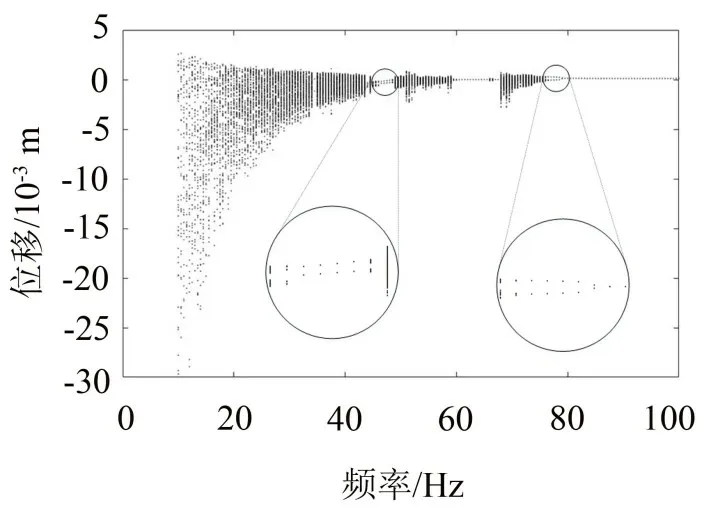
图7 接触支撑梁关于激励频率的分岔图

改变支撑弹簧k1的刚度系数，令F=150 N，f=10 Hz，以x1处的速度作为状态变量绘制分岔图，如图8所示。在弹簧刚度k1小于1.3×107N/m的区间内，接触支撑梁作混沌运动，但在[0.66,0.8]×107N/m 的区间内则突然变为周期1运动。之后便进入了周期运动，其中在约1.64×107N/m处进入周期2运动，并最终在3.3×107N/m处重新进入周期1运动。这说明了支撑弹簧的刚度系数对接触支撑梁的振动状态也会产生较大的影响。

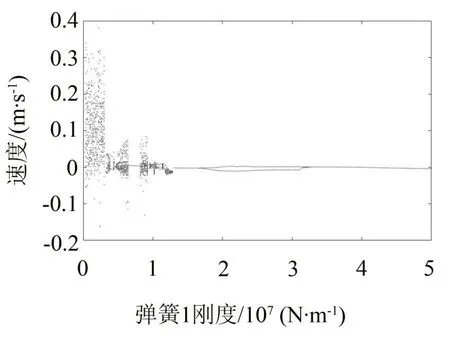
图8 接触支撑梁关于弹簧刚度k1的分岔图

5 结语

工程中某些情况下梁和弹性支撑之间并不是理想的线性耦合关系，本文考虑了弹性梁与支撑弹簧之间的接触行为，假设梁的支撑弹簧仅能承受压缩，探讨非线性边界条件对接触支撑梁的振动特性的影响。建立了三支撑弹性接触梁的分段线性动力学模型，采用Runge-Kutta法求解结构在简谐激励下的动态特性。通过与有限元软件的仿真结果对比，验证了该方法的有效性。

本文还讨论了激励参数和弹簧刚度系数对接触支撑梁非线性振动特性的影响。结果表明，激励幅值较大或激励频率较低时，都有可能会使接触支撑梁的振动从周期运动进入混沌运动，弹簧刚度系数也会对接触支撑梁的振动状态产生一定的影响。得到弹性接触支撑梁在不同参数下的振动特性后，可以通过合理的结构参数设计来避免系统进入混沌等不稳定的振动状态，以上研究可为梁类结构的振动控制提供参考。