考虑后视和多前车信息反馈的车辆跟驰模型

惠 飞,席 辉,张凯望,魏 思

(长安大学信息工程学院，陕西 西安 710064)

0 引 言

随着我国经济发展，交通运输业蓬勃发展，但交通运输量的增加和交通建设的滞后使得交通拥塞问题逐渐突显，成为人们关注和亟待解决的问题[1-2]。交通理论中，缓解交通拥塞在某些方面可理解为解决交通失稳问题[3-4]。为探究交通失稳的形成成因与演化规律，国内外许多学者依托车辆跟驰模型，以微观交通流角度用数学模型来表达模拟交通流的演变情况，对交通波动进行了深入研究[5-8]。

基于交通流与阻塞交通存在阻塞转移的特性，Brackstone等人[5]提出了微观交通流视角下的车辆跟驰的基本概念。Chandler等人[6]和Newelld[7]提出了刺激-反应原理，其考虑跟驰前后车的速度差及间距对跟驰状态的影响来描述车辆跟驰模型。Bando等人[8]于1995年提出了基于跟驰前后车间距最优化速度函数的最优速度(Optimal Velocity，OV)模型，可以模拟如走走停停、交通失稳之类更为真实的交通场景，为车辆跟驰研究打开了思路，诸多改进模型被研究提出[9-10]。其中，1998年Helbing等人[11]改进了OV模型中会产生的过大加减速问题，提出了考虑负速度差对跟驰行为影响的广义力(Generalized Force，GF)模型。Jiang等人[12]在2001年改进了GF模型，引入正速度差对车辆跟驰的积极效应，提出了全速度差(Full Velocity Difference，FVD)模型。Peng等人[13]为进一步提高交通流稳定性，在FVD模型上引入最优速度记忆项差值，提出了考虑驾驶员记忆的最优速度(Optimal Velocity Changes with Driving Memory，OVCM)模型，相比FVD模型具有更大的稳定区域。

随着车联网技术的发展，智能网联环境日渐成熟[14]，车辆可通过车车通信、车路通信技术获取到超视距范围下邻近多辆车的行驶状态信息[15-20]，诸多学者着眼于网联车新特性展开研究[21-24]。王涛等人[25]基于超视距下能获取更多车辆信息的特点改进了FVD模型，提出了引入多前车速度差信息的多速度差(Multiple Velocity Difference，MVD)模型，研究表明，引入多辆前车的状态信息能有效吸收跟驰车辆突变扰动，提升车流稳定性。孙棣华等人[26]从获取跟随车辆信息的角度研究，在FVD模型加入后视效应对交通流的影响，提出向后观测速度差(Backward Looking and Velocity Difference，BLVD)模型，结果表明，该模型可以有效减少交通流不稳定区域。在上述模型的基础上，考虑后视效应和最优速度记忆[3]以及考虑多前车速度差和最优速度[13]的车辆跟驰模型被相继提出。但是，同时考虑后视、多前车速度差和多前车最优速度记忆综合反馈的交通流特性并未在以上模型中体现。

综上所述，本文在OVCM模型的基础上，提出一种考虑后视效应和多前车速度差及最优速度记忆(Backward Looking-Multi-preceding Vehicle’ Velocity Difference and Optimal Velocity Changes with Memory，BL-MVDOVCM)的跟驰模型，并对模型进行线性稳定性分析，同时分析了多车和后视参数对交通流稳定性的影响，最后利用数值仿真验证模型，进行了与OV、FVD、OVCM模型的稳定性对比分析。

1 BL-MVDOVCM模型建立

基于车联网交通环境下，每辆车可获取到超视距的车辆行驶状态，因此考虑引入紧邻多前车的速度差及最优速度记忆信息和后视效应来改进OVCM模型，提出BL-MVDOVCM模型的微分方程描述为：

(1)

对式(1)展开描述：

=α[pVF(Δxn(t))+(1-p)VB(Δxn-1(t))]

-V(Δxn+i-1(t-τ))]

(2)

式中α为最优速度敏感系数；VF(·)和VB(·)分别为跟驰车及紧邻跟驰车的后车的最优速度函数；Δxn(t)表示前后车间距；t为当前时刻，v为t时刻车速，k为考虑紧邻前车的数量，T为人为和机械因素产生的延时，λi以及γi分别为第n+i-1辆车与其前车速度差项的敏感系数及最优速度记忆项的敏感系数；τ为最优速度记忆采样时间间隔。若不考虑后视效应和多车信息，则可取p=1、k=1，则简化为OVCM模型；若再忽略最优速度记忆影响，取p=1、k=1、γ=0(或τ=0)，则模型简化为FVD模型；当在前述基础上，不考虑前后车速度差因素，取p=1、k=1、γ=0(或τ=0)、λ=0时，模型简化为OV模型。

根据文献[3]采用最优速度函数计算公式如下：

(3)

其中，α′、α″分别为VF、VB的最优速度函数系数，h为跟驰前后车车头安全间距。

为降低模型的稳定性分析和数值分析的复杂度[3]，对公式中的T进行简化：

vn(t+T)=vn(t)+Tan(t)

(4)

将式(4)带入式(2)得：

(5)

-VF(Δxn+i-1(t-τ))]

(6)

简化Δxn(t-τ)，对其进行泰勒展开，并忽略非线性项：

Δxn(t-τ)=Δxn(t)-τΔvn(t)

(7)

同理对V(Δxn(t-τ))进行简化：

V(Δxn(t-τ))

=V(Δxn(t)-τΔvn(t))

=V(Δxn(t))-τΔvn(t)V′(Δxn(t))

(8)

将式(8)带入式(6)得：

(9)

2 线性稳定性分析

本节采用Lyapunov第一法及线性谐波微扰法[27]对车辆跟驰模型进行线性稳定性分析，具体是对稳态交通系统在周期边界条件下施加微小的扰动，使稳态交通系统产生微小的状态失衡，观察系统中扰动传播的变化规律并分析[15]。

施加一初始扰动yn(t)=eikn+zt后，每辆车的位置改变为：

(10)

由式(10)可得：

Δxn(t)=h+Δyn(t)

(11)

(12)

将式(11)、式(12)带入速度公式，得：

V(Δxn(t))=V(h+Δyn(t))=V(h)+V′(h)Δyn(t)

(13)

(14)

联立式(13)式(14)得:

(15)

带入式(11)式(12)式(15)到式(10)，可得扰动相关的微分方程yn(t)如下：

(16)

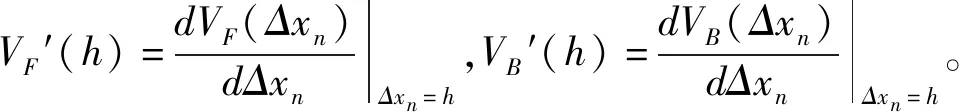
简化式(16)中yn(t)，设eikn+zt=eβ，则yn(t)=eikn+zt=eβ，有：

(17)

式(16)中yn(t)按傅里叶级数展开，并将式(17)带入可得：

z2eβ=αeβ[pVF′(h)(eik-1)+

(18)

式(18)等式两端约掉eβ，得：

z2=α[pVF′(h)(eik-1)+

(19)

对参数z按z=z1(ik)+z2(ik)2展开，同时将eik进行泰勒展开，均带入式(19)，则可得到z1、z2的表达式：

z1=pVF′(h)+(1-p)VB′(h)；

(20)

当z2<0，交通流系统车辆跟驰状态不稳定。反之，系统保持稳定状态。则新建模型的中性稳定条件为：

(21)

若要交通流系统在一微小扰动下仍能保持稳态，则满足的条件为：

(22)

反之，则不稳定。

取h=4，α=0.85，α′=1，α″=1，BL-MVDOVCM模型的λi和γi参数值[3，13]分别取为{λ1，λ2，λ3}={0.2，0.15，0.1}，{γ1，γ2，γ3}={0.1，0.08，0.06}，其他参数取值[12-13，25-26]如表1所示：

表1 各模型的其他参数表

根据表1参数，在MATLAB中绘制4种模型的临界稳定性曲线如图1所示，其中曲线以上为稳定区域，以下为不稳定区域。

图1 OV，FVD，OVCM，BL-MVDOVCM模型稳定性曲线图

处于稳定区域内的交通流在受到随机扰动后，经一段时间调整会被系统逐渐消化，交通流最终趋于稳定。而在非稳定相位区域内，随机扰动随时间对交通流影响会增加，使得交通流趋于产生时走时停的车流现象，最终导致交通拥塞的发生。从图1可看出，各模型稳定相位区域按OV，FVD，OVCM，BL-MVDOVCM模型次序依次增大，BL-MVDOVCM模型的不稳定区域最小。

图2和图3为k和p取不同值时所提模型的临界稳定性曲线图。从图中可看出：当初始条件一致时，在一定范围内增加k或减少p，不稳定区域缩小。由此可得，引入后视效应项和多前车综合信息项有益于进一步提高稳态交通流系统的抗扰动能力，保持车辆跟驰的稳定。

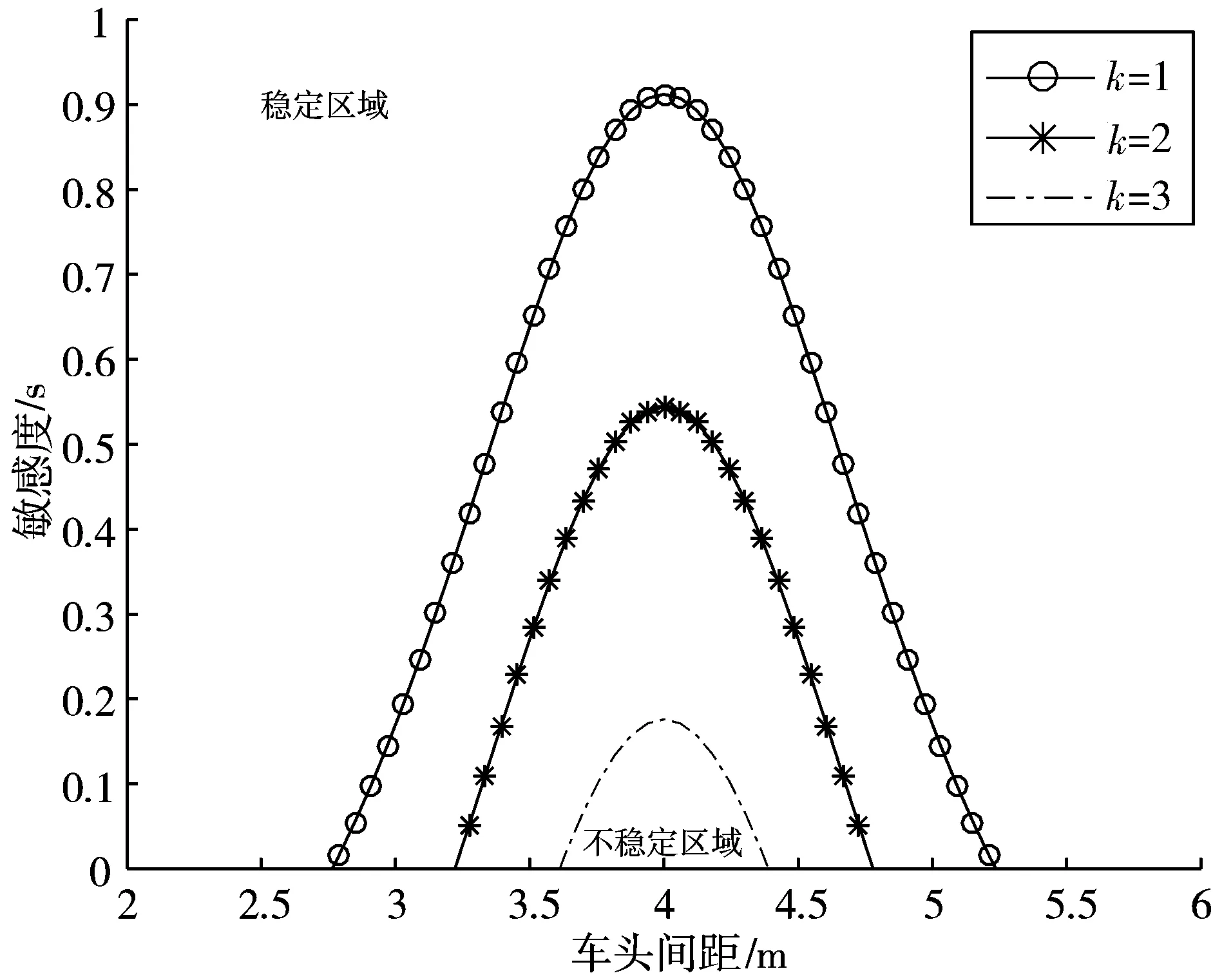
图2 不同k值下的BL-MVDOVCM模型稳定性曲线图

图3 不同p值下的BL-MVDOVCM模型稳定性曲线图

3 数值模拟与分析

利用数值仿真对BL-MVAOVCM模型的稳定性进行模拟验证和分析。根据跟驰模型特性选取一长L为400 m的环形车道，车辆总数N为100，各车以4 m为安全车头间距，有序分布在环形车道[27]。设定最高车速为2 m/s，即α′=1、α″=1，最优速度敏感系数α取0.8 5-1进行实验[3]。

数值模拟实验中，稳态交通系统车辆初始位置与车速为：

(23)

(24)

对第一辆车施加一个微小扰动：

x1(0)=1

(25)

即改变第一辆车的位置，观察稳态交通流系统受扰后状态变化并分析。

3.1 多车速度差、多车最优速度记忆及后视效应对系统稳定性影响分析

为验证BL-MVDOVCM模型中前车速度车信息、前车最优速度记忆信息以及后视效应信息对交通流的稳定性影响效果，分别在前述实验交通场景下用控制变量法对λ、γ、p敏感系数设定不同数值进行实验并分析。

3.1.1 前车速度差信息致稳实验

取考虑的前车数量k=1，后视效应敏感系数p=0.9，最优速度记忆敏感系数γ=0.3，记忆步长τ=0.3，在其他条件一致下将前车速度差敏感系数分别设置为λ=0、λ=0.1、λ=0.2，绘制车流在100 s、300 s时刻的速度变化曲线，受扰车流车速随前车速度差敏感系数λ的变化情况如图4所示。

(a) t=100 s

由图4可看出当λ值为0时，仿真时间100 s时刻的车流中车辆速度波动大，且在300 s时刻时，可明显看出车辆的速度显示出时走时停的趋势。

而随着λ值在0到0.2增加过程中，跟驰车流在仿真时间100 s和300 s的速度波动明显减小，特别是λ=0.2在300 s时刻的波动近乎平缓，说明在当前时刻交通流系统受初始扰动干扰而造成的速度波动已被系统消化，系统恢复为稳定交通，即考虑前车速度差可使稳态交通系统受扰振幅变小，因此模型引入速度差项可有效减少时走时停现象，增强交通流稳定性。

3.1.2 最优速度记忆信息致稳实验

取前车数量k=1，后视敏感系数p=0.9，速度差敏感系数λ=0.2，记忆步长τ=0.3，最优速度记忆敏感系数γ分别设为0、0.15、0.3，其他条件一致，绘制车流100 s和300 s时刻速度变化曲线，分析车流受扰后车速随最优速度记忆敏感系数γ的波动变化。

(a) t=100 s

由图5可得γ=0.3或0.15时，跟驰车流速度波动明显小于γ=0时的车速波动，即引入记忆效应能使车辆的速度波动范围区间变小，改善交通流的稳定性。同时明显看出γ为0.3的模型，在300 s时刻的车辆速度曲线较100 s时刻更平缓，且比γ取0.15的曲线峰要少，故选取γ=0.3作为之后实验敏感系数数值。

3.1.3 后视效应致稳实验

取前车数量k=1，速度差系数λ=0.2，最优速度记忆系数γ=0.3，记忆步长τ=0.3，将后视效应系数p分别取p=1、p=0.9、p=0.8进行数值模拟，绘制在500 s内的100辆车的速度曲线波动如图6所示，观察分析后视效应敏感系数p对交通流的致稳效果。

(a) p=1

由图6可看出随着p取值减小，100辆车速整体趋于一个稳定速度的耗时缩短，速度变化幅度范围减少，因干扰引起过大车速变化的车辆数更少。p=1的模型中，稳态交通受干扰后，跟驰车流内受影响车辆范围广，车辆受波动引起的速度差幅度平均在20%。而p=0.9时速度幅度明显降低，受干扰影响变小。p取0.8时，车流车辆速度曲线经200 s仿真时间的调整已趋于平缓。因此可得，引入后视效应能使受扰交通的速度波动幅度与影响时长降低，有助于交通流的稳态保持。

3.2 多前车综合信息及后视效应对系统稳定性影响分析

采用前述环形车道场景，根据参考文献[26]选取后视效应敏感系数条件p=0.9，对模型引入不同数量的邻近前k车行驶状态综合信息进行数值模拟，分析的交通车流中特定车辆(第25、50、75辆车)在仿真时间内的速度变化及其与前车车间距波动情况如图7～图9所示，其他参数采用表1中BL-MVDOVCM模型参数值，进行数值模拟。

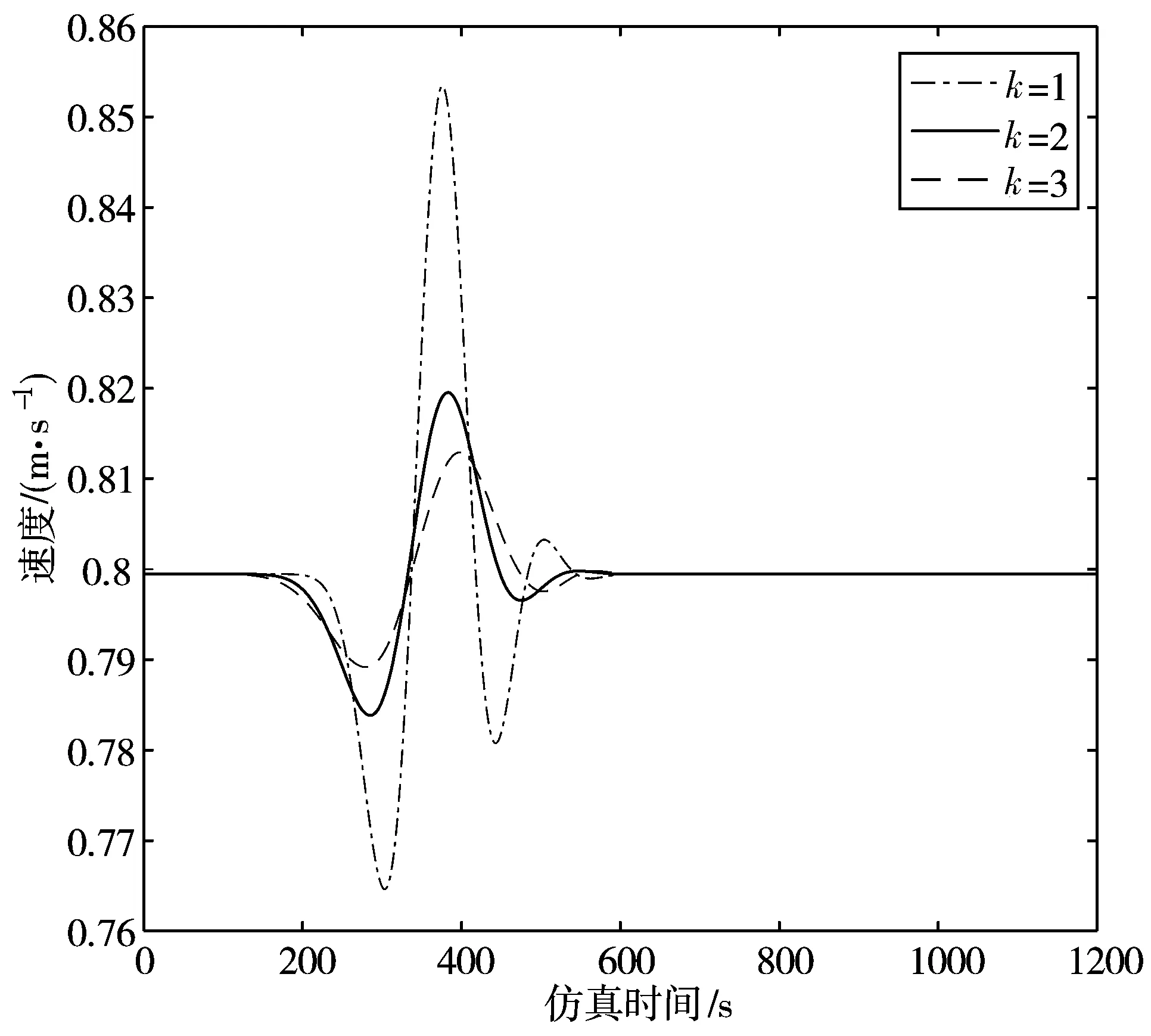
图7 第25辆车车速、距离随参数k变化波动图

图8 第50辆车车速、距离随参数k变化波动图

图9 第75辆车车速、距离随参数k变化波动图

由图7～图9可看出，k=3时的仿真结果的车流速度和车间距离的波动小于k=1、k=2时的车流波动，说明在k从1到3增加的过程中，即以跟驰车为主体，从考虑邻近1辆前车与其前车速度差及最优速度记忆综合信息，到考虑邻近3辆前车与其前车的综合信息的过程中，增加考虑邻近前车与其前车速度差等信息使得速度扰动振幅降低，距离的范围区间缩小，即减少了随机干扰的影响，使得交通流稳定性增强。结果说明：在其他条件一致下，引入多个前邻近车辆的速度差及多个前邻近车辆的最优速度记忆效应的综合信息能有效提升交通流的稳定性。

3.3 模型对比

在相同仿真场景下对经典OV、FVD、OVCM模型以及BL-MVDOVCM模型进行仿真实验，分析引入后视效应和多前车信息反馈的模型交通流的稳定能力，并与其他模型进行性能对比。

仿真环境与上述场景相同，各模型仿真参数按表1取值，统计采样时刻分别为30 s、100 s、500 s时不同模型百辆车的最大车速、最小车速、平均车速、以及速度波动率数据如表2～表4所示。

表2 第30采样时刻不同模型的速度及其波动率

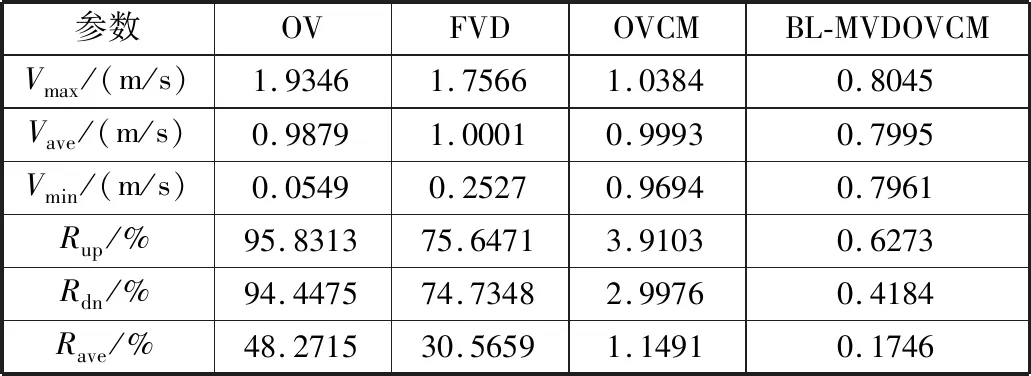
表3 第100采样时刻不同模型的速度及其波动率

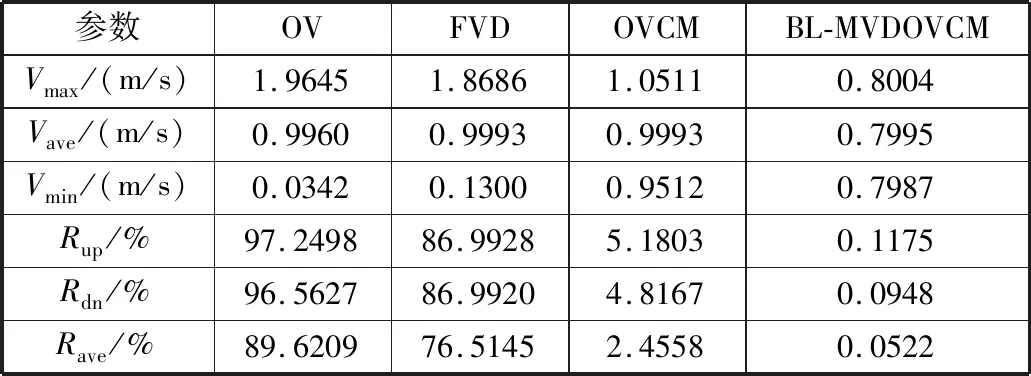
表4 第500采样时刻不同模型的速度及其波动率

从表2～表4可看出，不同采样时刻内下OV模型、FVD模型的速度波动率随采样时间递增而增大，特别是采样时刻500 s，OV模型的平均速度波动率达到了89.62%，而FVD模型也达到76.61%，表明此时的交通流已经出现了时走时停的交通现象，跟驰车流失稳。

而对于OVCM模型和BL-MVDOVCM模型，表中的速度波动率随采样时间递增而减少，同时500 s时刻2个模型的平均速度波动率均低于5%，说明模型的交通流系统正在消化初始扰动的影响。在3次采样时刻，相比OVCM模型、BL-MVDOVCM模型的向上和向下速度波动率均在1%附近，平均速度波动率低于0.5%，均明显小于OVCM模型的波动率采样值，说明扰动对所提模型的影响更小，BL-MVDOVCM模型的干扰控制能力更强。因此，所提模型引入多前车综合信息反馈和后视效应的考虑对稳态交通受扰维稳具有更优作用效果，改进了OVCM模型的抗扰能力，提高了交通流的稳定性。

4 结束语

本文为提升交通流的稳定性，基于OVCM模型上进行维稳性能改进，综合考虑融合超视距多前车信息与后视效应的影响，提出了考虑多前车信息反馈和后视效应的扩展跟驰模型(BL-MVDOVCM)。由临界稳定性曲线分析证明相对于OV、FVD、OVCM模型，BL-MVDOVCM模型具有更小的不稳定性区域。数值模拟实验结果得出：后视效应、速度差及最优速度记忆的考虑对交通流的致稳有明显效果。验证了综合考虑多前车信息和后视效应能有效改善OVCM模型的稳定性控制，所提BL-MVDOVCM模型的跟驰车流具有较好的稳定性。但本模型考虑仍有欠缺，如未考虑后视效应与交通流稳定速度的关系平衡，同时鉴于仿真场景设定的局限也未考虑到实际交通场景中不同交通环境对交通流稳定性的影响，这将是本文下一步改进模型和研究的方向。