基于FLANN改进的KNN医疗分类算法

郭 凯，艾菊梅

(东华理工大学信息工程学院，江西 南昌 330013)

0 引 言

近年来，国家卫生健康委员会统计出我国脑中风的发病率持续升高[1]，脑中风疾病将对患者产生极大的影响，摧残患者身心，且对患者家庭和整个社会都是一笔不小的负担，那么如何能早期预测患者患病风险就变得非常重要。因此，通过充分挖掘历史病历数据，综合人群各项身体指标，建立起体系全面完善的脑中风预测手段[2]，能够协助医护人员判断一般人群是否有罹患脑中风的可能性，以实现早诊断、早治疗、早预防的目的。基于现有的脑中风数据，利用分类算法等构建基于深度学习的脑中风预测方法[3]，有利于帮助医护人员对心脑血管疾病的预测和公众对脑中风的预防。

KNN算法简单易实现，在疾病预测领域使用广泛[4]，本文将KNN算法用于脑中风的预测中。KNN算法优点是可以处理具有2个以上类的数据集，并且对输入数据不强加任何假设分布。KNN缺点也相对明显[5]，KNN算法对样本进行分类时，要计算它与其他所有样本之间的距离，根据距离远近进行判断分类，这样非常消耗时间，影响算法效率。文献[6]提出了一种基于聚类去噪的改进KNN(C_KNN)算法来实现疾病情况的预测，该文先对数据进行聚类找出噪音数据进行清除，减小数据集，以此减少算法工作量和噪音数据干扰，提高算法准确率和效率。文献[7]提出了一种基于布雷-柯蒂斯(Bray Curtis)距离的加权k-最近邻分类算法(B_KNN)来实现癫痫的检测，该文主要是将KNN分类器中的欧氏距离替换为布雷-柯蒂斯距离。在高维空间中数据之间的布雷-柯蒂斯距离可以直接表示数据之间的相似性[8]。布雷-柯蒂斯距离具有在特征参数之前挖掘相关性的特点，对于度量高维空间中数据的相似性具有重要意义,以布雷-柯蒂斯距离取代欧氏距离能提高算法的准确率。

上述2种算法在大数据分类预测和癫痫诊断方面有非常大的意义和作用，但在脑中风领域中，因为引发脑中风的因素[9]很多，特征向量多且权重各不相同，一些病患的数据可能表现在不同特征向量上，简单聚类去噪可能会对待测数据中较为重要的数据进行清除，影响算法的准确率[10]。直接用布雷-柯蒂斯距离取代欧氏距离也不理想，需要科学有效地对各特征向量进行权重分配[11]。

针对上述问题，本文采用FLANN在总样本中循环搜索待测样本的最近邻点[12]，记录若干个最近邻点作为最近邻点子集，用最近邻点子集与待测样本进行匹配，降低计算量，提高算法效率，降低其他样本对待测样本的干扰，提高算法准确率[13]。KNN在处理高维数据时，对数据的各特征向量平等对待，容易出现误差，影响算法的准确率[9]，本文采用AHP方法[14]为各特征向量分配权重，正确处理各特征向量的影响，提高算法的准确率。本文充分考虑KNN算法在脑中风领域应用的不足，在专家们的研究基础上进行相应的改善：在考虑全体样本的情况下使用最近邻点子集替代全集[15]；针对脑中风数据集特征向量多且权重各不相同的特点，使用AHP方法为各特征向量科学有效地分配权重。这在脑中风领域将更加适用。

本文针对这2个KNN的缺点进行相应优化后采用一组脑中风的数据集进行实验，实验结果表明，F_KNN算法比传统KNN算法和上述的C_KNN算法、B_KNN算法准确率更高且速率更快。

1 相关工作

1.1 AHP

层次分析法(The analytic hierarchy process)简称AHP，是美国运筹学家托马斯·塞蒂(T.L. Saaty)在20世纪70年代中期正式提出的。AHP是将与决策有关的因素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。将结果作为目标层，各特征向量作为准则层，而后两两比较特征向量，构造准则层判断矩阵，通过不断实验，最后得出最恰当的权重分配[16]。

1.2 FLANN

FLANN(快速最近邻搜索包)是一个对大数据集和高维特征进行最近邻搜索的算法的集合。在机器学习中，对于一个高维数据集，FLANN库可以快速找到待测样本的最近邻样本。

FLANN库中的优先搜索K-means树算法[17]，它利用数据固有的结构信息，根据数据的所有维度进行聚类，对于需要高精度计算的情形效果极好[18]。K-means树算法分为2大部分，步骤归纳为如下8步：

1.建立优先搜索K-means tree:

1)建立一个层次化的K-means树。

2)将每个层次聚类中心作为树节点。

3)当某个集群内的点数量小于K时，将这些数据节点作为叶子节点。

2.在优先搜索K-means tree中进行搜索。

4)从根节点N开始检索。

5)如果N是叶子节点则将同层次的叶子节点都加入到搜索结果。

6)如果N不是叶子节点，则找出最近的那个节点Cq，同层次的其他节点加入到优先队列中。

7)对Cq节点进行递归搜索。

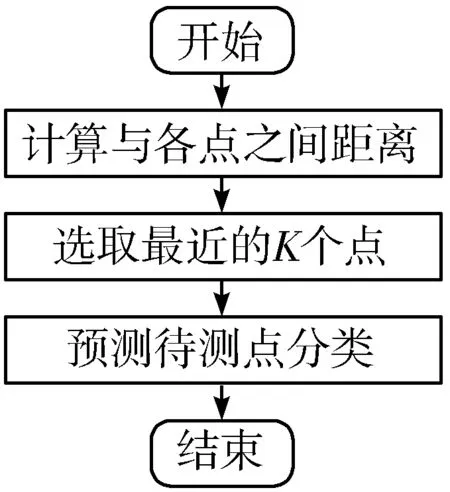
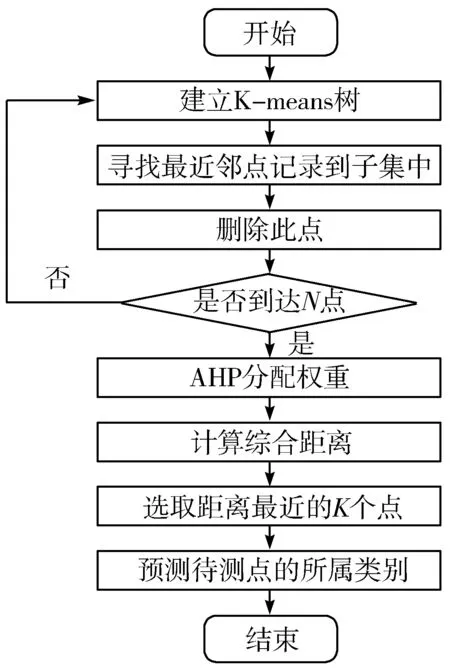
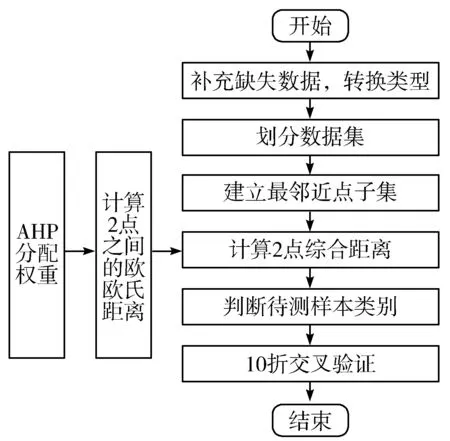
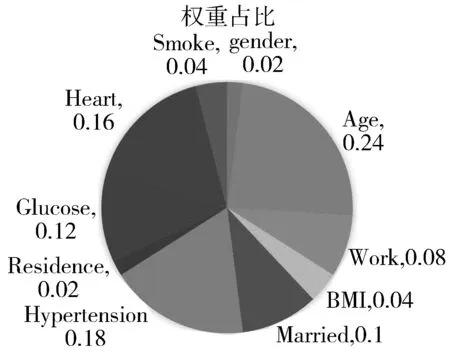
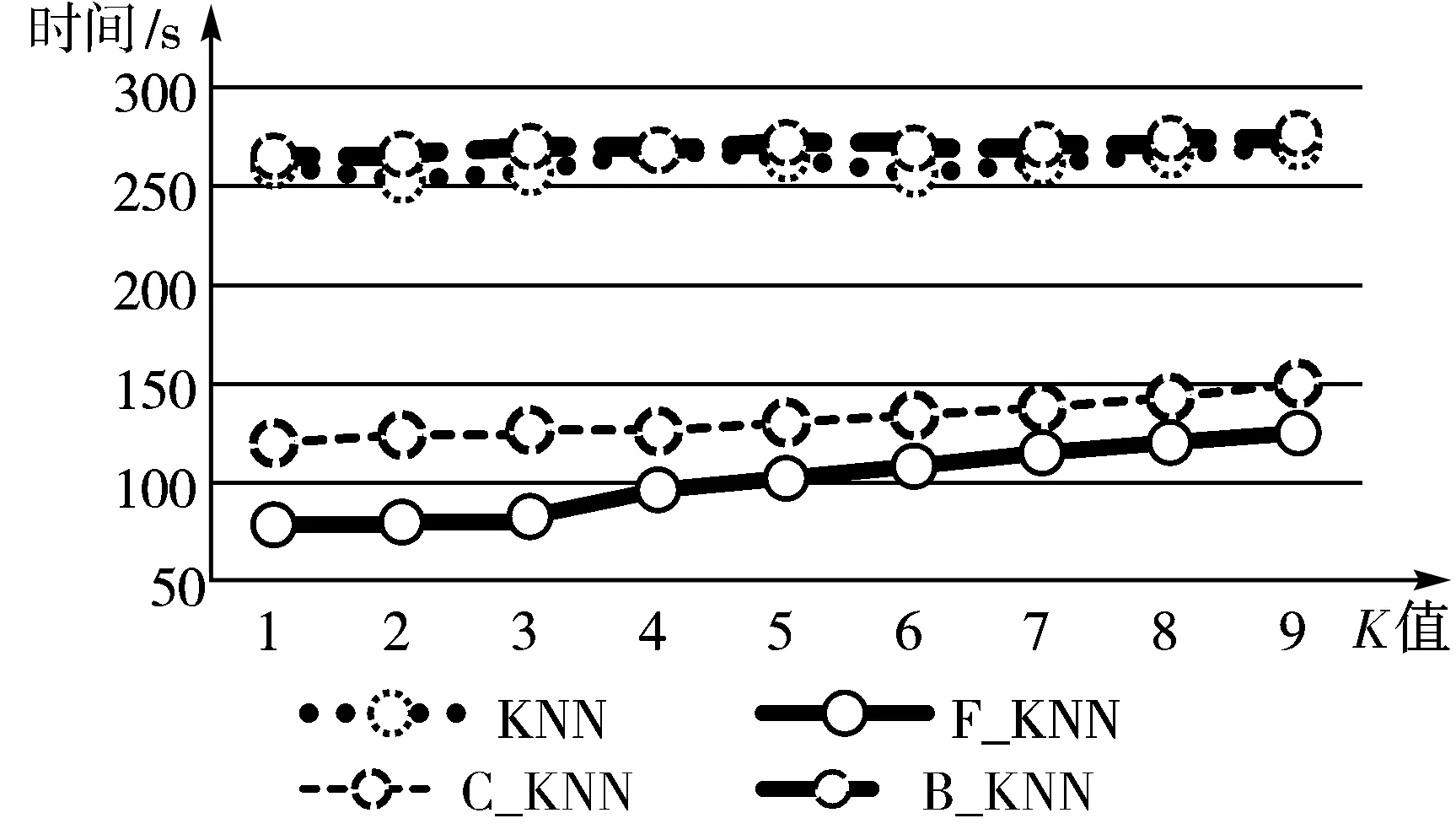
8)如果优先队列不为空且count

最终快速准确地找到待测样本的最近邻样本[19]。

1.3 KNN

KNN算法是一种基本的分类和回归方法，优点是简单，易于理解，无需建模与训练，易于实现；缺点是惰性算法，内存开销大，对测试样本分类时计算量大，性能较低。

KNN最邻近分类算法的实现原理[20]：为判断待测样本的类别，计算此样本与所有已知类别样本之间的距离，根据距离远近进行排序，若前K个最近邻已知样本中那个所属类别最多，即把未知样本也归为此类。KNN算法流程如图1所示，算法步骤归纳为如下3步：

图1 KNN算法流程图

1)计算测试数据与各个训练数据之间的距离。

2)选取距离最近的K个点。

3)返回前K个点中出现频率最高的类别作为测试数据的预测分类。

2 F_KNN算法

在本文提出的基于FLANN改进的KNN算法即F_KNN(循环搜索最近邻)算法，其主要思想是在已知样本中循环利用FLANN寻找待测样本的最近邻点，记录此点，再从已知样本中删除这个最近邻点，继续寻找第2个待测样本的最近邻点。将记录的若干个最近邻点作为最近邻点子集，利用最近邻点子集来判断待测样本的所属类别[21]。以最近邻点子集代替整个已知样本，计算出在计算距离时采用AHP分配特征向量的权重，求得子集中与待测样本综合距离最近的K个样本，把K个最邻近样本中所属类别占比较多的类别作为待测样本的预测类别输出。在F_KNN算法中，可减小计算量，极大提高算法的效率，降低各特征向量的影响，提高算法的准确率[22]。F_KNN算法流程如图2所示，算法步骤归纳为如下9步：

图2 F_KNN算法流程图

1)在已知样本中建立K-means树。

2)利用K-means树快速寻找待测样本的最近邻点，并将此点记录到最近邻点子集中。

3)在已知样本中删除此点。

4)重复N次步骤1～步骤3。

5)将记录的N个点作为最近邻点子集。

6)使用AHP为各特征向量分配权重。

7)根据各特征向量权重计算待测样本与子集中各样本之间的综合距离。

8)选取离待测样本距离最近的K个点。

9)返回前K个点中出现频率最高的类别作为待测样本的预测分类。

在脑中风预测领域，算法要结合患者的血压、血糖、心脏病等多个因素来进行预测诊断，简单去除噪音数据可能会影响检测结果[23]，而且特征向量较多且占比不同，需要一个科学有效的权重分配方法。F_KNN算法面对脑中风领域预测进行针对性的优化，对待测样本较为重要的样本都进行相应的处理且减小算法的工作量[24]，同时使用AHP方法对各特征向量分配最为合适的权重。优化后的F_KNN算法将更适用于脑中风领域的预测。

3 实验分析

3.1 实验框架

3.1.1 数据集

本实验应用的数据集为Kaggle官方提供的healthcare-dataset-stroke-data.csv数据集，含有5110组数据，每组数据包含12个信息，数据包含的信息如表1所示。

表1 数据集信息表

3.1.2 实验方案

实验中，使用JetBrains PyCharm 2017.1.2 x64作为程序后台代码开发IDE；测试平台CPU:Intel(R) Core(TM) i5-6200U 2.4 GHz，显卡:AMD Radeon R7 M370，操作系统：Microsoft Windows 10；记录测试平台上运行算法的准确率和时间。

3.2 实验流程

本文使用F_KNN算法对脑中风进行预测的思路为先初步处理数据，完善数据集，再使用F_KNN算法对数据集进行训练与测试，最后进行10折交叉验证求得算法准确率。实验的具体流程如图3所示，实验归纳为如下6步：

图3 实验流程图

Step1补充缺失数据。数据集中BMI(体重指数)缺失了3.93%，以中间值28.10替代缺失值并且对类别变量使用独热编码,将字符串类别转换为数值。

Step2划分数据集。对脑中风数据集的5110组数据进行划分，3577(70%)组数据作为训练集，1533(30%)作为测试集。

Step3建立最近邻点子集。本文循环使用FLANN来寻找与待分类样本最近的N个点作为最近邻点子集，因为各特征向量的权重不同，所以综合距离和实际的距离并不相等，为了减小误差，N一般要大于K,才能找到离待测样本综合距离最近的K个点。经过反复实验，本文采用N=6K，在缩小子集降低计算量提高效率的同时不影响准确率。

Step4计算距离。由于数据集是高维数据集，含有多个特征向量，每个特征向量对分类结果的影响差别很大，因此首先要确定每个特征向量的权重。本文采用AHP来确定各特征向量权重，把是否中风作为目标层，各特征向量作为准则层，而后两两比较特征向量，通过不断实验，最后得出最恰当的权重分配，如图4所示。

图4 特征向量分配图

经过实验对比，本文计算距离时采用欧氏距离效果最佳，故本文采用AHP计算各特征向量权重后，再计算2个样本之间的欧氏距离，最后根据各特征向量权重求2个样本之间的综合距离。

Step5判断待测样本类别。对所有距离进行升序排序得出离待测样本最近的前K个点，前K个点中出现频率最高的类别作为待测样本的预测分类。

Step610折交叉验证[25]。为了充分利用数据集对算法效果进行测试，进行10折交叉验证，再求其均值，作为对算法准确性的估计。

4 实验结果及分析

4.1 对比实验

本文引用上述提到的C_KNN和B_KNN同样对脑中风数据集进行实验，最后将F_KNN、C_KNN、B_KNN、传统KNN的结果进行比较分析。

C_KNN算法通过聚类，将训练集中同一类别的样本按照相似度分成若干个子类别，形成多个聚类中心。聚类后，出现一些没有分类成任何小聚类的样本。这些文本一般属于噪声样本，该类样本的代表性较小，可去除这些样本，在最后KNN算法对待测样本进行计算时，选取与待测样本最为接近的子集取代全集进行计算，将大大降低KNN算法的计算复杂度，提高KNN算法的时间效率。

B_KNN算法以布雷-柯蒂斯距离取代KNN算法中的欧氏距离，通过这种方法来挖掘样本之间的相似性对待测样本进行比较，可以一定程度上提高算法的准确率。首先利用Bray Curtis距离计算训练集中y(y=(y1,y2，…，yN))与采样点之间的距离。

其中，N为样本的特征个数。显然，b=0表示样本完全相同，而b=1是2个样本之间可以观察到的最大差异。

4.2 实验分析

本文从准确率、召回率和F1值3个方面对F_KNN算法进行评价。

准确率是正确样本数(Sc)比实际样本数(Sm)，计算公式为:Pc=Sc/Sm。利用最优参数训练好的F_KNN与C_KNN、B_KNN和传统KNN对脑中风数据集进行分类得到分类的准确率对比如图5所示。

图5 不同算法准确率对比图

从图5可以看出在面对脑中风数据集时，F_KNN表现最为良好，准确率波动不大且一直较高，在K取值为6时达到最大值0.9642。这表明F_KNN算法的分类性能更高，表现更好。

召回率[26]是用实验正确样本数(Sc)除以所有正确样本数(So)。计算公式如下：Pr=Sc/So。F_KNN算法与传统KNN算法的召回率对比如图6所示。

F1值[27]是一个综合评价分类效果的指标，计算公式如下：F1=Pc·Pr·2/(Pc+Pr)。F_KNN与C_KNN、B_KNN和传统KNN的F1值对比如图6所示。

图6 不同算法召回率与F1值对比图

从图6中可以看出F_KNN的F1值最高，召回率偏高，这表明F_KNN算法的邻域稳定性更优。

本文在实验代码运行中添加1个计时器，计算每次代码运行的时间，用来比较算法的效率。本文选择当K取不同值时运行F_KNN与C_KNN、B_KNN和传统KNN各20次，取平均时长，时长对比图如图7所示。

图7 不同算法运行时间对比图

从图7可以看出F_KNN算法的运行时间远低于传统的KNN算法和B_KNN算法，也低于C_KNN算法，这表明F_KNN算法的效率最高。

综上所述，优化后的F_KNN算法提高了分类准确率且极大提高了分类效率。在处理高维且数据较大的数据集时，优化后的KNN算法优势明显，具有较好的应用前景。

5 结束语

本文工作主要围绕脑中风疾病预测开展。首先系统地介绍KNN算法的基本原理并分析KNN算法在高维数据集运用中的缺陷。针对KNN算法的缺陷，本文使用AHP为特征向量分配权重；使用FLANN寻找最近邻点子集，取代全集，减少算法计算量，对算法进行优化。最后实验从准确率、召回率、F1值3个方面验证F_KNN算法比传统KNN算法更加有效。

本文优化后的F_KNN算法在医疗大数据方面的应用，不仅缩短了算法的预测时间，而且可以取得更好的预测效果。将F_KNN算法运用在疾病预测领域，可以简单快速地预测用户的身体状况，对用户起到一个早诊断、早治疗的效果，能帮助医护人员对用户的疾病进行初步的预测和预防。