基于数学核心素养培养的解析几何复习备考策略
⦿江苏省灌云高级中学
林利芹
1 引言
最近几年,高考数学试卷中一直将解析几何题放在“压轴”位置,题目占据的分值非常大,且具备较强综合性,时常让学生感觉到解题思路受阻.究其原因可知,学生没有掌握解析几何题的实质,不了解题目考点,自然也就无法运用正确的解题技巧,最终浪费大量时间,并且出现丢分的情况.在高考复习备考阶段,教师可以从数学核心素养培养的角度,帮助学生提升解决解析几何题的能力,促使学生抓住解题关键点,通过自身的抽象思维和推理思维,解析出最终的结果.
2 认清解析几何题目的数学本质
2017年我国修订了《普通高中数学课程标准》(下文简称“新课标”).新课标中明确提到数学学习过程中需要重视其数量关系以及空间形式的相关内容,数学在现实世界中呈现出抽象性,其内容本身就具备抽象结构,不管是模型构建还是符号运算,均能够呈现出现实世界的本质内容,探寻不同事物之间的关系和规律.而高中数学课程教学,需要遵从学生的主体性,注重学生的未来发展,将立德树人作为高中数学的根本教学任务,不仅要让学生掌握数学解题方法,也要培养学生创新思维,促使学生数学核心素养显著提升.事实上,数学核心素养包含了数学运算、数据分析、逻辑推理、直观想象、数学抽象以及数学建模等能力,各项能力之间呈现出相互交融但又相互独立的状态,在组成有机整体以后,学生必然能够认清数学题目的本质,并从容应对要解决的问题.
目前高中教材中数学知识板块的划分主要有14个,各个知识板块有效组合在一起,从而形成完善的数学教学体系.解析几何知识是高中数学重要的内容,其连接了代数板块的知识,将代数与几何有效整合在一起,形成数形结合的教学内容.解析几何的相关题目不仅能够利用函数的知识解答,也能够利用方程进行标注,通过对曲线知识的理解,构建对应的方程式,在经过方程式消元之后,整理成一元二次方程,最终利用判别式以及韦达定理等知识,获得答案.此时,如果是采取函数思维,则需要建立对应目标函数,并理解各个函数之间的关联,通过对极值、最值等因素求解,最终达到合理求解的目的.
3 基于核心素养培养的解题能力训练策略
3.1 核心素养培养中解题能力的获取
数学核心素养的培养最注重数学抽象素养的培养,因此,在复习备考训练中,也需要重视对学生抽象能力的培养.新课标中表示,数学教学过程中,抽象思维的培养主要是对学生进行数量关系的抽象锻炼和空间形式的抽象锻炼,学生需要理解各个数量所具备的联系,并且寻找图形构建的主要规律,探究数字和图形之间形成的逻辑关系,挖掘题目背后的本质规律,以数学语言表达出来,从而形成数学的基本思想.而数学抽象思维也将成为学生学习和应用数学知识解决解析几何问题的关键,能够让学生在面对解析几何题目的时候,透过题目当中对数量关系的描述构建几何图形,并且不断转换数形关系,利用数形结合思想形成明确的解题思路,最终透过数学符号语言,解答出解析几何的正确答案.
除了抽象思维能力,数学核心素养的培养,也需要重视逻辑推理能力的培养,该能力是学生掌握解析几何题目数学本质的精髓.新课标中已经明确指出,逻辑推理能力是指从命题本身出发,遵从命题当中的规则,推理出其他的命题.数学逻辑推理包含两个类别:一类是从特殊规律推理出一般规律,其主要是通过归纳和类比的方式来完成推理;另一类则是从一般规律推理出特殊规律,主要是通过演绎和逻辑推理的方式来获取最终的数学结论.逻辑推理是数学的精髓,也是人们掌握数学知识和参与数学活动的基本品质.
3.2 核心素养培养中解题能力的训练
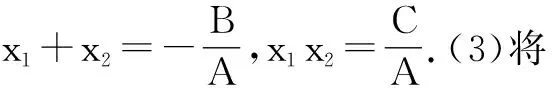
(2017年理科数学全国卷Ⅲ第20题)已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
(1)证明:直线AB过定点;
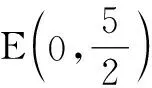
除了解题模式的训练,教师也需要帮助学生培养数学运算能力.一方面,教师在课堂上可以将更多的时间留给学生,促使学生自己参与到解析几何的运算当中.部分学生虽然运算能力并不好,但却能够将运算障碍暴露出来,只有亲身感受运算的艰难,才能够更好地了解自身不足.另一方面,教师可以为学生选择难度较高或者是综合性更强的运算题来训练,促使学生不断加大运算量,逐步提升运算能力.例如,2019年全国高中数学联赛A卷的第10题是一道运算量较大的解析几何题:平面直角坐标系xOy中,圆Ω与抛物线Γ:y2=4x恰有一个个公共点,且圆Ω和x轴相切于抛物线Γ的焦点F,求圆Ω的半径.学生根据教师所引导的解题思路,主要采用曲线系方程,逐渐化解题中的难点,充分凸显出学生所具备的创新能力.解题方法如下:
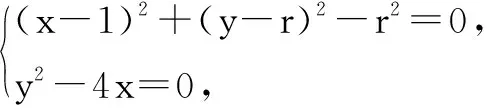
①
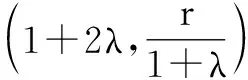
除了上述训练,教师还需要训练学生规范运用数学符号语言,在数学符号书写过程中需要注重细节.解析几何作为压轴大题,数学符号语言的表达直接关系到其是否能够利用方程或者不等式来完成逻辑推理,充分体现出学生在数学解题方面的思维严谨性.例如,建议学生不要在解解题过程中使用一些并不太常规的结论.在2018年高考数学全国卷中,一些学生直接使用了中点弦的有关结论,而在2019年的全国理科数学卷中,又有学生直接利用了抛物线y2=2px的中点弦相关结论.如果在选择题等方面使用不会暴露弊端,但如果运用到解析几何大题中,必然会对分数产生影响.
4 结束语
不管是采用函数还是方程方式求解解析几何的问题,都需要探究圆锥曲线与直线的位置关系,需要学生具备更加清晰的数学逻辑思维,并提升数学运算能力,在面对抽象数学问题时具备一定解题思路.总体来说,高考之前加强对解析几何知识的理解,能够促使学生更明确高考需要考查的知识点,促使学生掌握对应的数学能力,使其能够在高考期间有效攻克数学难点.

