基于转向熵的长隧道路段操纵特性分析

李永庆，阎莹

(长安大学 运输工程学院，陕西 西安 710054)

近年来，山区高速公路建设步伐日益加快，成为我国公路运输网络重要组成部分，也为我国交通运输业发展壮大奠定了基石。其中，隧道路段的兴建既克服了崇山峻岭导致的地理阻碍，又消除了海拔起伏导致的高程障碍，能明显减少两地或多地之间客货运输距离，节约运输时间，降低施工成本。然而，由于隧道特殊结构及由其产生的安全问题，使其成为扼制公路运输咽喉的关键部分。隧道路段交通事故发生率往往低于普通路段，但事故后果往往较为严重[1]。隧道声光环境交替变化剧烈，容易导致驾驶人操作行为发生异常，引发交通事故[2]。本文从驾驶员转向操作技能角度引入转向熵概念，探索山区高速公路路段运行环境对车辆操纵稳定性和驾驶安全的影响。

1 试验数据采集及处理

1.1 试验路段选取

本次试验以长隧道(1 000 m<隧道长度≤3 000 m)为隧道研究变量，因其长度适宜，可以作为研究隧道路段对驾驶人操作特性和生理影响的典型道路代表。选取包茂(包头-茂名)高速公路西安至安康路段，秦岭终南山隧道群中南五台隧道(2 564 m)为研究对象。

1.2 试验设备

驾驶员操作指标数据的收集采用无线传输方向盘转角仪，采样频率为20 Hz，体积小、重量轻，如图1所示。

(a)方向盘转角仪

1.3 试验人员招募

驾驶员来自于收费站和服务区，通过雇佣的方式招募组成。本次试验选出5名驾驶经验丰富的驾驶员参与，平均年龄40.7岁，平均驾龄20.6 a，并进行1至5编号。

1.4 试验过程

试验前1天对驾驶员进行流程及设备要领培训，告知安全和规范操作事宜。试验时，工作人员先为驾驶员佩戴并调试好设备，然后要求1至5号驾驶员按照自然驾驶习惯依次驾驶，并在试验过程中做好记录。

1.5 数据预处理

无线信号采集设备在使用过程中难免发生基线漂移(零点漂移)现象，如图2所示。因此，为了消除设备异常影响，需进行基线校正，如图3所示。

图2 发生基线漂移的方向盘转角Fig.2 Steering wheel angle with baseline drift

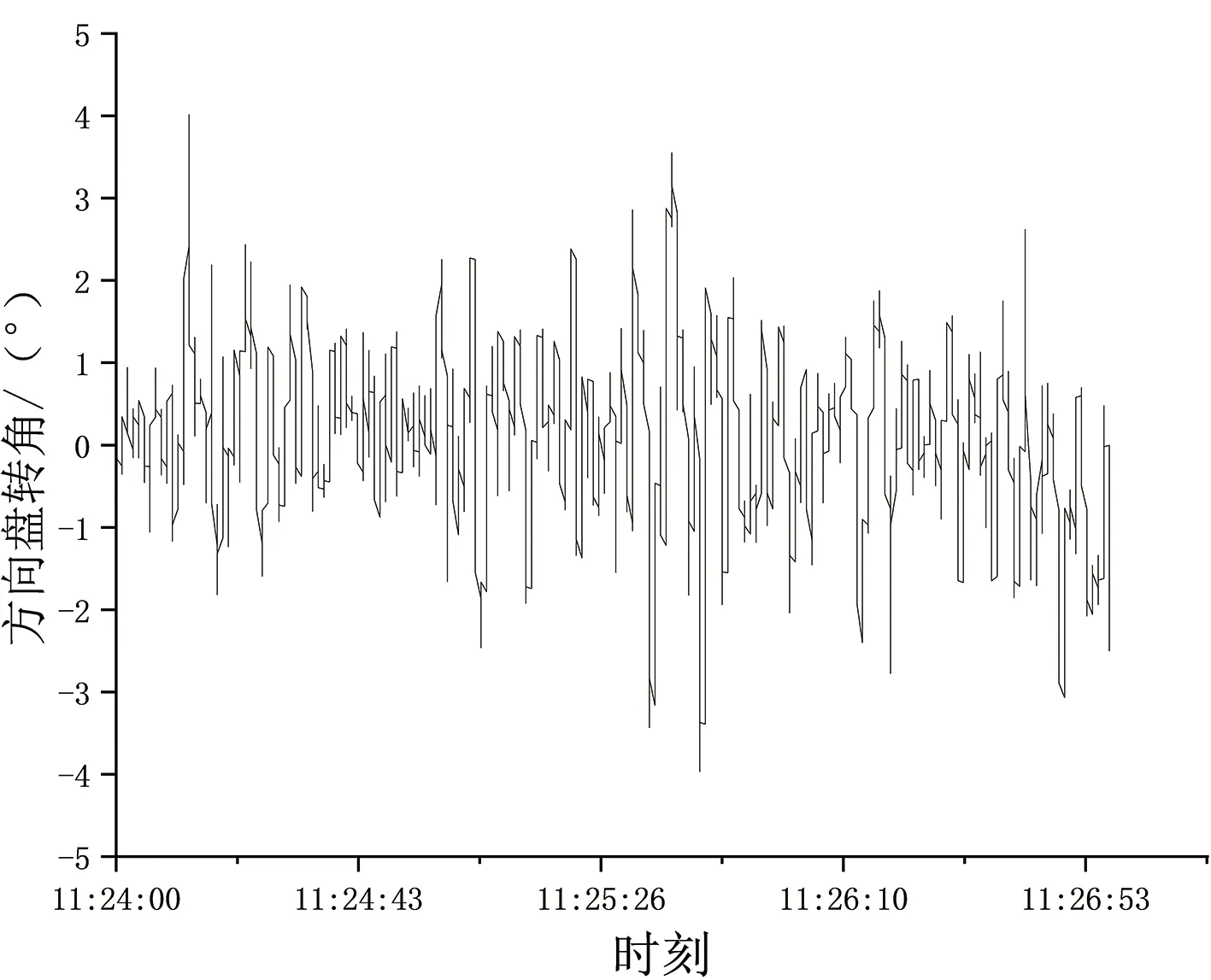
图3 基线校正后的方向盘转角Fig.3 Steering wheel angle after baseline correction

另外，在驾驶过程中，难免会因为道路线形引起驾驶员较大的转向差异。因此，为方便同时研究直线和弯道路段驾驶员横向稳定性保持特征，需要消除线形影响。消除规则为：如果在4 s内驾驶员具有相同转向时针，并且4 s内每秒均值之和大于等于20°，即可认为其中掺杂了线形影响信息，需滤除。将每秒数据减去均值即可得到弯道时转向保持数据，如图4所示。

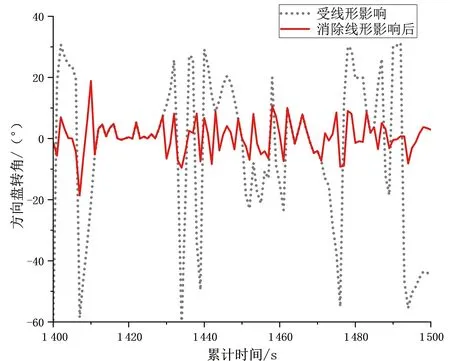
图4 弯道转向信息消除Fig.4 Elimination of curve turning information

2 转向熵特征提取

为了研究驾驶员在隧道出入口顺适应过度，本文将研究范围扩大至洞外100 m，其中：入口段由入口前100 m至入口后400 m组成；出口段由出口前400 m至出口后100 m组成，其余为中间段。为方便研究，将整段隧道(含连接段)划分成140个区间。

方向盘转角特征表现了驾驶员转向操作特性，适用于评价、判别驾驶员驾驶负荷状态或风险状态，常用指标包括方向盘转向熵及方向盘转角标准差等[3]。

本文以方向盘转向熵为特征变量，定量描述驾驶员在时间序列上的转角变化。熵的概念最初从物理学和化学角度进入人们的认知，熵代表的是体系的混乱程度。熵为零，代表系统是有规则的，是秩序的；熵无穷大，则表明系统是完全随机的[4]。所以，可以用转向熵来定量分析驾驶员横向操纵稳定性。因为熵在这里已经标准化，表示程度概念，故无量纲。

以每个小区间的转角数据作为分析对象，在已知的时间刻度上，利用前三处(θ(n-3)、θ(n-2)、θ(n-1))的方向盘转角值，在n-1时刻，通过二阶泰勒公式展开，可预测时刻n时方向盘转角θp(n)的值[5]：

θ(n-2))-(θ(n-1)-θ(n-3))] ，

(1)

即

(2)

若在时刻n实际测得的方向盘转角值为θ(n)，则预测的θp(n)与实际值θ(n)之间的误差e(n)为

e(n)=θ(n)-θp(n)。

(3)

根据方向盘转向熵理论，e(n)服从正态分布。现找出置信水平α值，使之将e(n)划分为以下9个区间：(-∞,-5α]，(-5α,-2.5α]，(-2.5α,-α]，(-α,-0.5α]，(-0.5α,0.5α)，[0.5α,α)，[α,2.5α)，[2.5α,5α)，[5α,∞)。α的值可由下面的概率公式确定：

P{-α

(4)

然后根据各区间的频数确定转角值在对应区间的分布概率pi，方向盘转向熵值由式(5)确定。

(5)

计算转向熵可得驾驶员在隧道路段驾驶时横向稳定性表现情况。对5名驾驶员在隧道路段行驶的转向熵计算结果取均值后，可视化结果如图5所示。从图5中可以看出，隧道路段整体转向熵普遍较高，各段均值在0.7以上。驾驶员转向熵从进入隧道至中间段行驶45个区间(约900 m)部分呈波浪式上升趋势，而后短时间内有所下降，从距离出口30个区间(约600 m)至出隧道又呈波浪式上升趋势，说明隧道出入口处的交通环境对驾驶员的横向稳定性存在一定影响。通过对比驾驶员在不同路段的转向熵分布情况来看，中间段均值(0.728 72)要低于入口段(0.736 54)和出口段(0.754 67)均值，也说明中间段的横向稳定性要高于其他两段。

图5 隧道路段方向盘转向熵Fig.5 Steering entropy of steering wheel in tunnel section

由此可见，驾驶员在隧道路段行车时往往倾向于频繁微调以修正转向，以获得驾驶安全感，从而导致驾驶横向稳定性差。研究表明，隧道内交通事故率要低于开放路段[6],所以频繁的修正并不会真正地导致驾驶事故，比如侧翻，碰撞隧道壁等，反而可能会促使驾驶员大脑皮层神经兴奋，抵抗驾驶疲劳，有利于安全驾驶。

作为对比，取隧道外2 000 m连接段长度用以研究开放路段驾驶员操纵特性，如图6所示。开放路段视野开阔，环境照度良好，驾驶员工作环境较隧道路段优越。但是，根据开放路段驾驶员熵值走势情况，并未从中得出驾驶员操纵规律。虽然转向熵仍然呈波浪式上升下降，但并不能得出如同隧道路段般驾驶员熵值分布规律。从图6中可以看出，开放路段各区间转向熵均值波动性较隧道路段大，且均值(0.739 75)较大，说明驾驶员在开放路段驾驶时，并没有因舒适的驾驶环境给道路交通增加安全性。

图6 开放路段方向盘转向熵Fig.6 Steering entropy of steering wheel in open road section

3 熵值特征指标分析

隧道路段由于其特殊盾构物形式，导致其运行环境和开放路段有较大差异，突出特点就显示在驾驶员受环境影响而表现出的驾驶规律。图7展示了4种路段的转向熵分布情况。

图7 各段转向熵分布Fig.7 Distribution of turning entropy in each section

在进入隧道前，驾驶员观察到隧道的存在，并迅速感知危险采取措施。受“黑洞效应”影响，驾驶员在进入隧道时产生一定时间的视觉盲期，导致驾驶员心里紧张，视觉负荷增加[7]。从“明环境”进入“暗环境”，驾驶员经历了视觉震荡的适应期，此时的转向操纵稳定性在开放路段的基础上发生略微恶化，使转向熵出现了增大的趋势，增幅为0.21%。

行至中间段，隧道环境表现出了低照度的鲜明特点。通常晴朗天空下室外环境照度可达10万lx，而隧道中间段照度通常最高不足500 lx，这无疑增加了驾驶员视觉负荷[8]。此时增加的驾驶负荷并没有导致驾驶员在转向操纵稳定性上出现恶化，反而使驾驶员在转向有序程度上呈现了有利变化。中间段的转向熵均值在4个路段处于最低状态，说明安全系数超出了其他路段。在入口段基础上，中间段熵值明显降低，降幅为1.62%。

中间段后期，驾驶员已经可以远眺隧道出口。此时的驾驶员多伴随紧张、惊恐、逃逸心理，期望迅速驶出隧道[9]。此时的驾驶行为属于“逆照度”驾驶，必然产生“眩光”现象，导致交通参与物不能清晰地在视网膜成像。在较大的心理负荷和恶劣的运行环境耦合作用下，驾驶员转向操纵有了新的恶化，并且操纵无序程度处于四段中的最高状态，较其他路段危险系数更高。熵值增幅在中间段基础上相当明显，增幅为3.55%。

出隧道后，驾驶员心理、视觉负荷下降，驾驶员转向操纵有序程度应当高于其他路段，但实际情况是较隧道中间段表现出恶化现象。开放路段驾驶员视野更加开阔，除去了隧道路段 “墙壁效应”的影响，以及“实线不可变道”的法规限制，于是在驾驶行为上较隧道路段更加“自由”。因此，开放路段驾驶员转向操纵稳定性并没有得到显著提升，反而无迹可寻。

图8横向对比了4种路段熵值概率分布，发现隧道路段(含前后开放路段)驾驶员转向熵总体大概率分布在0.67～0.77,说明隧道路段行车驾驶员横向操纵无序性高、稳定性差、危险性高。另外，开放路段驾驶员转向熵出现了明显的双峰现象，这是隧道其他路段不曾有的，说明开放路段行车时，驾驶员横向操纵行为有“两极分化”的趋势，再一次印证了开放路段横向操纵稳定性差、危险系数高的结论。

图8 各段熵值概率密度分布Fig.8 Entropy probability density distribution of each section

4种不同场景下驾驶员转向熵对比及变化见表1。在上述均值比较中，出口段均值表现出熵值大、稳定性差的现象。但是，综合考虑转向熵标准差、变异系数、极差结果来看，开放路段的综合不稳定特征更加明显。所以，设计者在进行开放路段安全合理性设计时，更不容易把握运行环境对驾驶员客观作用规律，容易造成设计出现缺陷等问题。而隧道运行环境对驾驶员的作用表现出了显著客观规律，有利于隧道设计者把握横向操纵规律，进行合理的安全设计。

表1 不同场景下熵值特征指标对比Tab.1 Comparison of entropy characteristic indexes under different scenarios

图9展示了4种路段的转向熵核密度图。显然，入口段和出口段更接近正态分布，再一次说明了隧道行车规律性更加可控，而中间段和开放路段出现了“分化”的趋势或已经出现了“分化”。对比4种路段累积分布函数图(如图10所示)发现，4种路段转向熵80%分位数均落在了0.8的后面，而60%分位数依旧高于0.75。因此，可以断定隧道路段行车时具有高转向熵的特点。

(a)入口段

4 结论

1)在心理与隧道环境耦合因素影响下，驾驶员转向操纵行为表现出了特定作用规律。其中，入口段整段至中间段600 m处，驾驶员转向熵呈波浪式上升趋势；中间段后半程呈波浪式下降趋势，且速度较快；出口段总体呈上升趋势，且熵值在隧道段达到峰值。

(a)入口段 (b)中间段

2)开放路段并没有因为驾驶员较低的运行环境干扰压力和心理负荷而表现出较低的转向熵和稳定的变化规律，相反却因为驾驶压力的减小而表现出更复杂的操纵特性，意味着开放路段的驾驶员横向操纵行为危险性并没有比隧道路段低。

3)通过对比隧道和开放路段驾驶员转向操纵特性，发现隧道内驾驶员受环境作用规律性明显强于开放路段。表明隧道设计人员可以将此规律应用于设计理念，保障隧道安全运行；而开放路段表现出的复杂特性要求公路开放路段设计者加强客观合理性设计。