基于模糊故障树和灰色关联算法的CASS污水系统分析
鲁明,吴志光
(池州职业技术学院 机电与汽车系,安徽 池州 247000)
随着“中国制造2025”和“工业4.0”计划战略的提出,国内外专家和学者开始重视利用智能技术解决故障诊断问题。污水处理是一个复杂的、多变量耦合、非线性的生化过程,当污水处理厂发生故障时,出水水质指标达不到标准,会造成二次污染。因此,如何解决和实现污水处理系统的故障诊断与识别是一个不可回避的难题。
近年来,大数据技术和多元统计理论的故障诊断方法得到了广泛的应用,特别是在机械、风电、航空技术、数控机床、化工、医药等领域,正朝着高效率的方向发展,因此必须依靠故障诊断知识和专家系统为其保驾护航。由于现代设备诊断规模大,每台设备可能出现多个故障点,数据采集频率高,因此必须通过检测故障诊断来获取海量数据,为此国内外专家付出了艰辛的努力,取得了巨大的研究成果。例如,许玉格等[1]将核理论与极限学习机相结合,对污水处理过程进行在线诊断。鲁明[2]将神经网络与PCA方法相结合,利用神经网络对关键出水指标值进行预测,消除了污水处理过程中的非线性和动态影响,该方法优于传统的PCA方法。王彤等[3]提出了基于模糊灰色关联的汽车驱动桥系统故障树分析方法,将模糊理论和灰色关联算法有效地结合起来,分析了基于模糊灰色关联的故障树建立过程,并将其应用于汽车驱动桥系统,证明了系统的可靠性。Cai等[4]提出了一种基于故障树的可靠性风险分析方法,解决了模糊和不确定信息的风险建模问题。Zhou等[5]提出了一种基于PCA的贡献图方法来识别与故障相关的关键变量。Sang等[6]提出了一种基于KPCA的故障识别方法,其构建鲁棒误差故障识别方法的基本思想是当重构变量为故障变量时,该变量的故障指数小于非故障变量的故障指数,实践证明该方法准确、效率高、应用广泛。上述研究都是对系统的模糊性进行分析,但是污水系统就是一个模糊性、复杂性、同时又具有灰色性的系统,由于故障信息的缺失,使得故障事件之间的相关性存在不确定性。
本文研究的是具有强非线性、先验知识少、模糊性和灰色性的非平稳CASS(cyclic activated sludge system),也称周期循环活性污泥法工艺工业废水处理过程,提出一种基于模糊灰色关联的污水处理系统故障树分析方法,将灰色理论与模糊数学理论相结合,采用模糊灰色关联的故障树分析方法,用三角模糊数表示污水处理底部事件的概率。
1 污水处理故障建立与分析
1.1 故障树分析(FTA)
故障树分析(FTA)是通过演绎的方法逐级分层找出故障的可能发生原因,以最后找到最基本的原因为止。该方法将系统中可能发生的故障或最不期望发生的事件作为故障树的顶事件(包括环境、软硬件、人为因素等),导致故障状态的所有可能原因作为中间事件,导致中间事件发生的最终原因作为底事件,然后通过事件之间的逻辑关系,建立系统故障的数学模型。其中,割集是指故障中一些底部事件的集合[7]。当这些底部事件有一个发生时,顶部事件必然发生。最小割集是指将集合中所含的底事件去掉1个就不能成为割集,一般来说,最小割集可以用下行法找到,即从顶事件开始,逐层找到割集,遇到“与门”时,增加割集的阶数,遇到”或门”时,增加阶级的个数。具体方法是:从故障树的顶事件开始,依次用顶部的上一个事件替换下一个事件;当遇到“与门”时,将事件横向连接在一起,当遇到“或门”时,将事件竖直串联接在一起,直到所有逻辑门都被底事件替换为止;这样,表的最后一列中的每一行都是故障树的割集,然后对割集进行比较,进行元素的合并和剔除,得到故障树的全部最小割集。
1.2 模糊数
模糊数的表示方法有多种形式,教材和文献中最常见的方法大概分为三类:三角模糊数、梯形模糊数和正态模糊数[8],本文采用的是三角模糊数,三角模糊数的隶属函数如图1所示。图1中Up(x)为x的隶属函数,a和b为模糊数的下限和上限。

图1 三角模糊隶属函数Fig.1 Triangular fuzzy membership function
通常在分析大型污水处理系统时,由于系统的复杂性和运算量大、过程复杂等原因,很难求解出顶事件发生的概率,但是可以运用三角模糊数解决这一难题,它的特点是计算和结构简单,对定量分析有着重要作用。其隶属函数表达式为
(1)
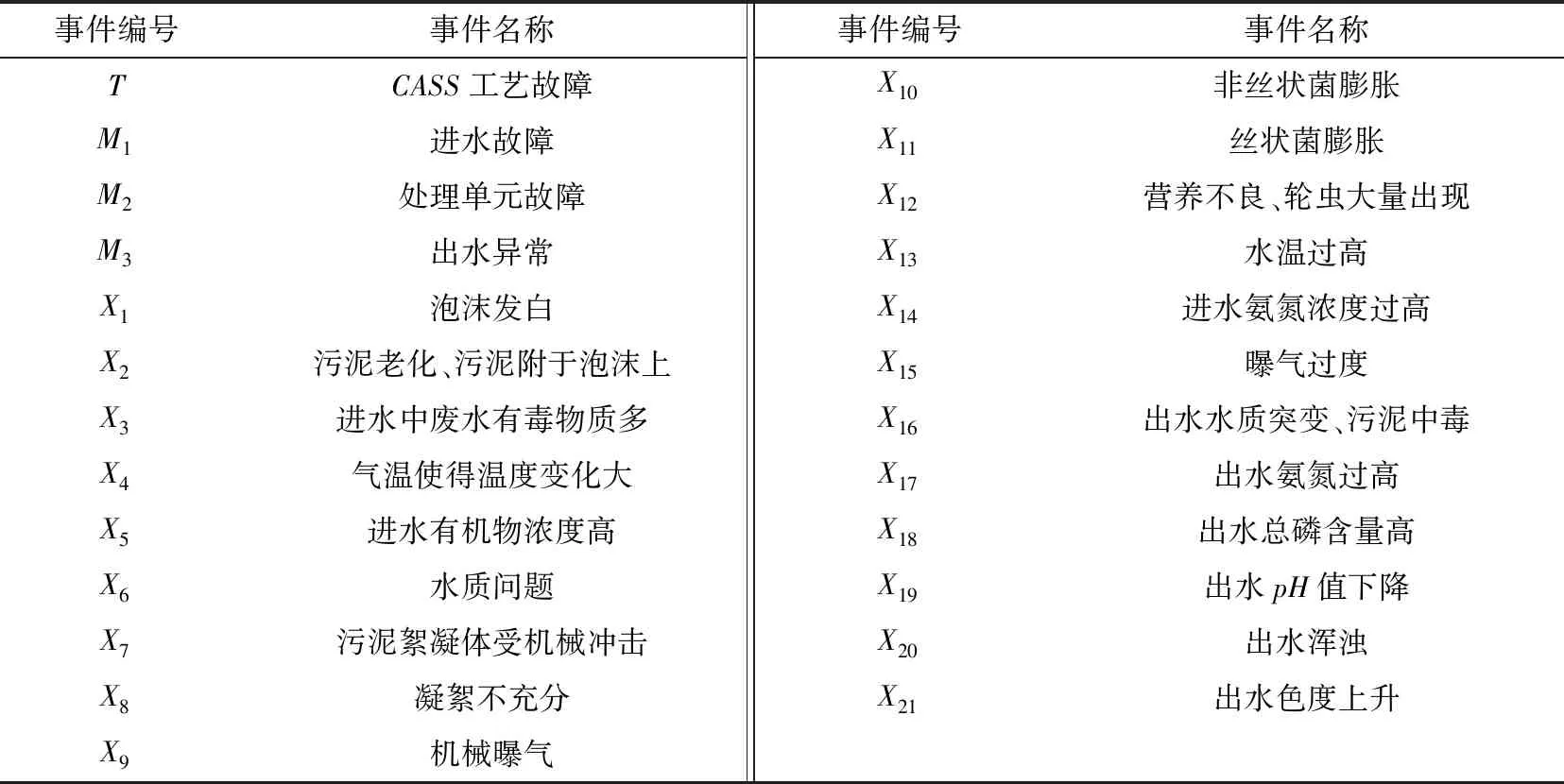
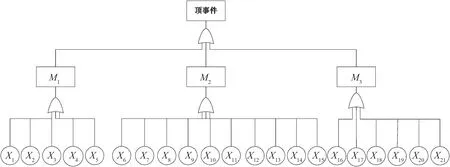
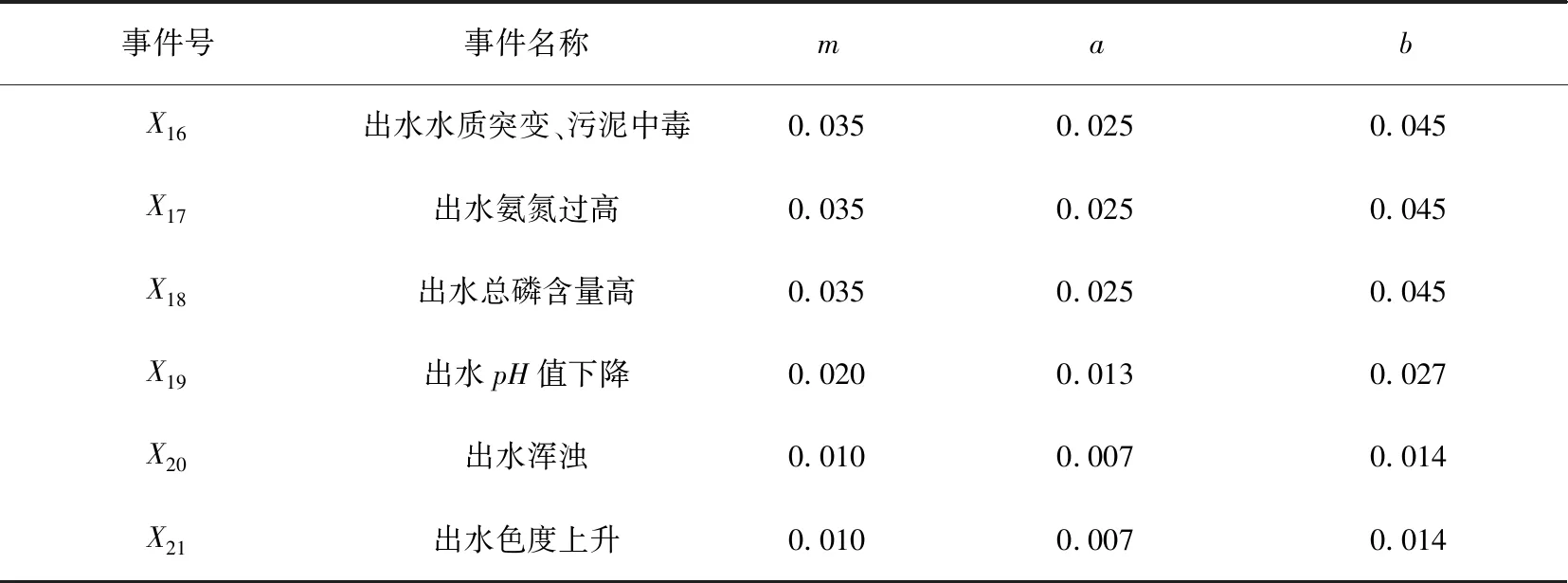
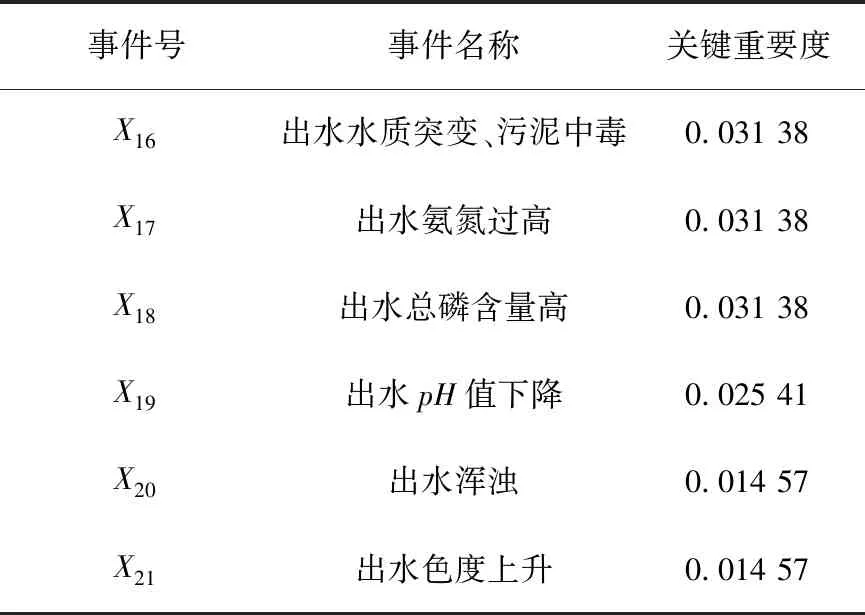
则设底事件xi(i=1,2,3,…,n),底事件发生的概率Pxi=(m-a,a,m+b),其中a,b为Pxi的上下限,m为底事件发生概率的中值,有0 (2) (3) 根据函数H(x)=H(x1,x2,x3,…,xn)以及底事件发生的概率,可判断顶事件T发生的概率:PT=(aT,mT,bT)。 (4) 式中:当第i个最小割集里包含的基本事件都不发生时,顶事件仍然能发生的概率PT=(aT,mT,bT);记模糊概率的中值为mT0,则顶事件在底事件xi没有发生故障时,仍会发生的概率PTi=(aTi,mTi,bTi)。 灰色系统就是利用数据信息量少、信息不全、各个元素之间无相关性的特点,实现对部分信息确切描述和理解。对于大型的污水处理系统而言,它的系统存在模糊性和非线性,在进行可靠性分析时,各个故障树之间、故障事件和顶事件之间的关联性也不确定[9];因此,将关联分析引进到故障树分析中很有必要。灰色关联分析就是通过灰色关联序列比较不同元素之间的强弱关系,将故障树中各个最小割集的模糊重要度均值化处理,作为灰色模型的子序列,其表达式为 XT=[XT(1),XT(2),…,XT(n)]= (5) (6) 则灰色模型的子序列可构成的矩阵为 (7) 为了诊断出各个元素的影响因素,将构成的矩阵Xm和XT进行灰色关联度的比较,通过关联度的计算,将关联度进行排序,就能得出不同故障模型对顶事件影响的重要程度。 在构成的两个矩阵Xm和XT中,将对应于第i个基本事件的差值的绝对值作为差序列,即 ΔMT(i)=|Xm(i)-XT(i)|。 (8) 在针对多元矩阵序列分析时,计算关联系数的公式为 (9) 式中ρ为分辨系数且0<ρ<1,通常取ρ=0.5。灰色关联度是表示两个灰色系统之间相似性的指标,变化范围为[0,1],越接近1影响越敏感,反之就越不敏感。由于关联度的数量多、信息分散,所以在计算其关联度时按照平均值法求解比较方便,可以得出 (10) 最后,根据求解的γk对最小割集进行排序,求出的灰色关联度越大,则最小割集对故障影响越敏感;反之则越不敏感。 在分析故障树时,底事件的发生会影响顶事件的发生,任何与最小割集结合的割集都是导致顶事件发生的最小割集。最小割集中的基本事件发生时,那么顶部事件一定发生[10]。对于一个故障树系统而言,设总共有M个元件,系统发生故障记为故障树的顶事件并记为T,构成的元件为底事件记为X1,设系统的元件有正常和非正常两种状态,分别用0和1表示,则 (11) 然而,由于顶事件的状态是底事件的状态函数,可以用T(x)=T(x1,x2,…,xn)描述,则 (12) 根据上述对故障树的描述,本文以污水处理系统的CASS工艺作为研究对象。CASS工艺的优点是能去除污水中的可降解有机物,同时也能去除易降解的可溶性有机物,促进系统中絮凝细菌的生长,提高系统运行的稳定性和可靠性。CASS工艺系统的运行分为4个不同阶段,即进水阶段、曝气阶段、沉淀阶段和闲置阶段,在此期间,污泥不断循环运行。池内污泥经过好氧和厌氧两种过程,有利于除磷菌的生长。在曝气阶段,通过硝化反应实现除磷脱氮;在非曝气阶段,还存在反硝化作用,将活性污泥带回生物选择都不在考虑的故障范围之内[11],即省去了在故障树设计中人为因素导致的故障。 根据资料和某污水处理厂的实时统计显示,CASS污水工艺故障如图2所示,各种故障事件见表1。 表1 故障事件表Tab.1 Failure event table 如图2所示,从故障树的底事件开始,最底层的每一个基本事件都是割集,只有当底事件都发生时,顶事件才会发生,但是如果随意删除一个基本事件,该割集就不是最小割集。由此可以得出故障树的最小割集是21个,分别为: 图2 CASS污水工艺故障树Fig.2 CASS wastewater process fault tree K1={X1},K2={X2},K3={X3},K4={X4}, K5={X5},K6={X6},K7={X7},K8={X8}, K9={X9},K10={X10},K11={X11},K12={X12}, K13={X13},K14={X14},K15={X15}, K16={X16},K17={X17},K18={X18}, K19={X19},K20={X20},K21={X21}。 顶事件是所有底事件和的表达形式,则该故障树可表示为H(X)=M1+M2+M3=X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11+X12+X13+X14+X15+X16+X17+X18+X19+X20+X21。如果对系统进行全部分析则较为复杂,因此本文仅对出水异常事件作为顶事件来进行分析,可知M3包含了6个最小割集,分别是{X16},{X17},{X18},{X19},{X20},{X21}。 统计近5年污水处理厂的数据以及可能发生故障的概率。根据经验可知,发生出水异常故障的概率为10%,且该故障概率中35%为水质突变、污泥中毒,表现为X16事件;35%为有机物含量过高,具体表现为X17和X18事件;20%为出水的pH值含量下降,具体表现为X19事件;10%为出水水质颜色的变化,具体表现为X20和X21事件。根据以上统计,采用三角模糊数表示上述事件的概率,得出如表2所示的故障发生概率。 表2 故障发生概率Tab.2 Probability of failure 根据式(2)和式(3)可以求出三角模糊概率PT=(0.109 78,0.164 53,0.204 37),进一步可以求出M3事件的概率模糊中值mTz=0.164 29,根据式(4)和式(5)可以求出最小割集。由于设计的故障树只有或门,所以每一个基本事件只有一个割集,各个割集的模糊重要度依次为(0.031 38,0.031 38,0.031 38,0.025 41,0.014 57,0.014 57)。 由上述实例得出底事件为6个,即m=6,在特征矩阵最小割集中所含有的底事件均取1,其余为0,这样可得到矩阵 (13) 根据故障树每个底事件发生的概率,可以获得每个底事件的关联重要度(见表3)组成检测模式的向量,即 表3 关联重要度Tab.3 Relevance importance (14) 把各个底事件的模糊重要度均值后,再将标准模式中的向量进行量化处理,可以得到待检测模式向量 (15) 以Z[J]为参考序列,X为比较序列,根据式(6)和式(7)可以计算出各个灰色关联度,采用平均值法,取Δmin=0,Δmax=1,ρ=0.5,得出{γ16,γ17,γ18,γ19,γ20,γ21} ={0.713 20,0.708 25,0.714 14,0.695 25,0.695 25,0.674 14}。根据上述结果,对构成中间事件M3出水的6种模式的最小割集灰色关联度依次进行排序,可以得出相应的结果:γ16>γ18>γ17>γ19=γ20>γ21。可以看出γ16水质突变、污泥中毒对出水异常影响最大,也是导致CASS工艺污水故障的重要影响因素之一。而在M3事件中,γ21出水色度上升对出水异常影响最小,符合污水处理厂长期数据统计的规律。经过灰色关联度的分析可以得出如下结论:水质突变、污泥中毒,出水氨氮过高,出水总磷含量高对出水异常故障影响最大,所以在检测时,需要进一步加大检测精度,改善工艺水平。 本文利用灰色关联算法和三角模糊数解决了故障树难以获得准确概率的问题,以及各事件之间关系难以确定和发生故障概率大小问题。根据模糊关联故障树的分析算法,首先根据故障树求出最小割集,然后利用三角模糊重要度求出故障发生的概率,建立灰色关联模型,通过计算得出最小割集与中间事件和顶事件的灰色关联度,找出系统的薄弱环节。结果表明,运用故障树和模糊理论以及灰色关联算法三者相结合的方法对污水处理的分析是可行的。此算法比传统BP神经网络具有更好的故障预测效果,准确度高、稳定性好。1.3 模糊重要度

1.4 灰色理论分析
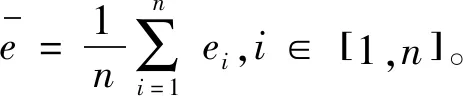
1.5 灰色关联的计算
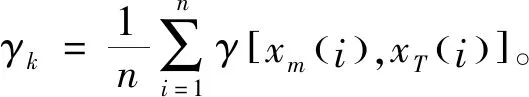
1.6 灰色关联分析在故障树中的应用

2 CASS污水工艺处理系统的故障树分析
2.1 模糊概率的计算
2.2 特征值的故障矩阵
2.3 计算关联系数


3 结束语

