穿越沙波区的海底管道冲刷研究
刘极莉,孙祥杰,余志兵,于洪旭,李秀锋
(海洋石油工程股份有限公司,天津 300451)
0 引言
穿越沙波区域的海底管道,可能形成自由悬跨,有时在强烈底流的作用下,管道周围的非黏性沉积物极易发生冲刷[1]。海底管道周围沉积物的冲刷是由管道本身的存在引起的,对海底管道的安全运营存在重大影响。例如,冲刷对海底管道现有悬跨的改变、由于冲刷而形成新的悬跨、冲刷导致海底管道的下沉或自埋[2],从而对管道稳定性产生影响等。因此,在海底管道设计过程中,尤其是穿越沙波区域的海底管道,在许多方面都需要研究冲刷问题。
1 管道冲刷下降和掩埋的机理
管道冲刷的基本机理取决于冲刷的间距,即孤立冲刷和相互作用冲刷[3]。孤立冲刷由于管道跨中的下垂而导致管道降低或埋设,相互作用冲刷由于沉积物承载的失效导致管道降低或埋设。
在管道孤立冲刷的情况下,初始冲刷孔向下延伸至平衡冲刷深度,并沿管道长度增长,直到管道以自重下沉到延长冲刷孔内。管道的初始下陷通常会导致冲刷深度的整体增加,因为它会对冲刷孔周围的沉积物产生更大的剪应力,从而增加平衡冲刷深度。在某一时刻,管道在跨中处的下陷剖面不再增加海底剪应力,随着冲刷孔的继续延长,管道将逐渐下沉。管道周围可能会发生沉积物沉积,从而根据达到的平衡冲刷深度造成管道的完全掩埋或部分掩埋,见图1。
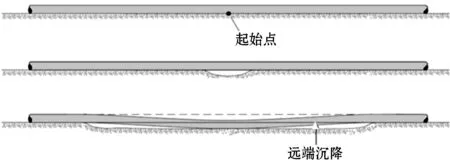
图1 孤立冲刷机理
在有许多冲刷起始点的情况下,每个冲刷孔沿着管道的长度增长到平衡冲刷深度,直到支撑管道的剩余泥沙达到极限承载力。之后持续的冲刷将会引起土壤承载破坏,导致管道下沉。土的任何承载破坏通常都会导致平衡冲刷深度的整体增加,因为它倾向于对剩余冲刷孔周围的泥沙产生更大的剪应力。当埋设管道对水流产生的扰动不足以产生超过冲刷开始时的泥沙剪切应力,此时管道埋设将趋于稳定,任何剩余的冲刷孔都可能被回填。在管道周围可能会发生沉积物沉积,导致管道全部或部分掩埋,见图2。
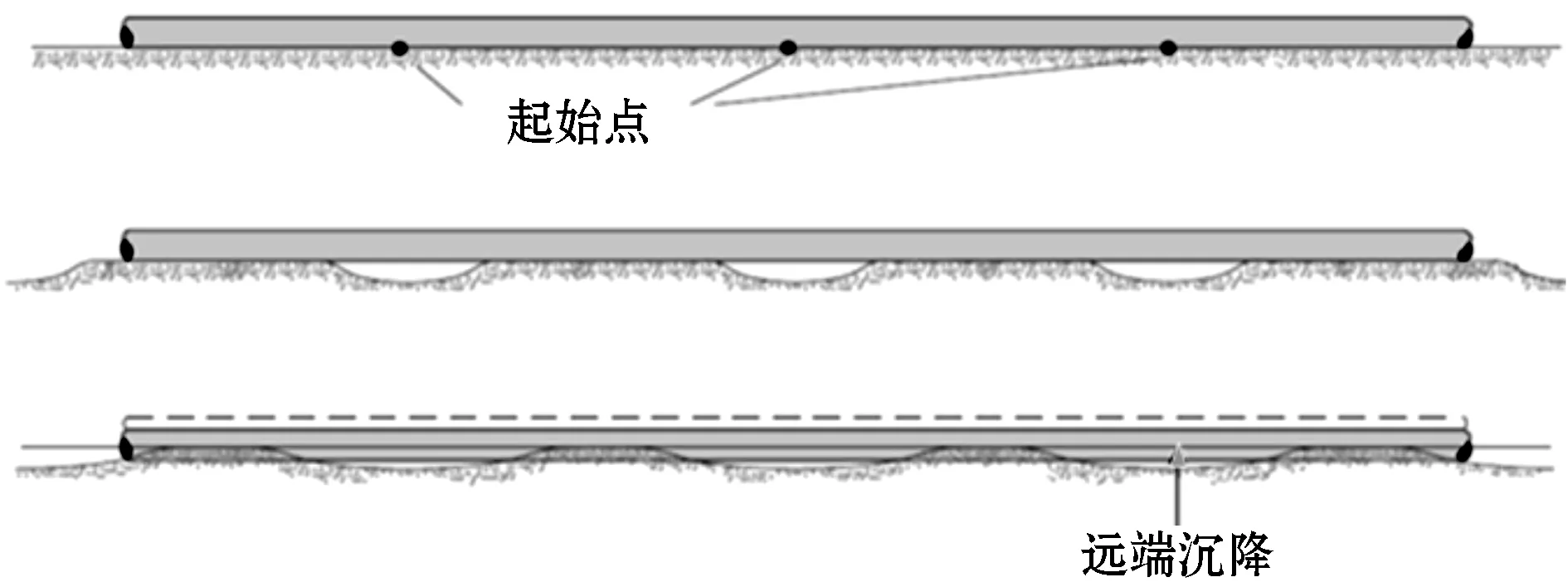
图2 相互作用冲刷机理
孤立冲刷倾向于使管道悬跨增大,相互作用冲刷倾向于使管道悬跨减小。孤立冲刷机制在理论上对可能发生的悬跨没有特定的限制,而相互作用的冲刷机制只能在冲刷终止之前发生。根据这一分析,孤立冲刷将主导管道的完整性。由于管道的自降也会发生,在接近着泥点时可以建立的海底剪应力将会减小,而随着管道进一步降低,管道附近的剪应力最终将达到一个应力水平,不再发生进一步的冲刷。这时,管道下降位置和局部冲刷孔都在着泥区,但悬跨不会进一步发展,因为海床剪应力不能超过临界水平。
2 冲刷的开始和发展
如果管道的初始沉降量较低,且管道周围的水流足够强,冲刷可能会穿透管道下方,这定义为冲刷的开始。冲刷的发生与管道上下游之间的压力差引起的管道底部砂土中的渗流直接相关。当流速逐渐增大达到一个临界点,此时渗流增加速度快于驱动压力差,沙子和水的混合物穿过管道下面的空隙,这在土力学中称为“管涌”。
Chiew对稳流条件下管道冲刷发生的条件进行了研究,包括渗流与冲刷开始的关系[3]。他将冲刷的开始与管涌现象联系起来,推断出管道上游和下游之间的压力差会导致管道下面的渗流,从而破坏管道下面海床的稳定。
Sumer等提出了恒定流中冲刷开始的解析表达式[4]。该表达式给出了给定沉降(e/D)以及土壤参数s和n条件下的临界流速Ucr。
(1)
式中:Ucr为开始冲刷临界流速,m/s;g为引力常数,m/s2;s为土壤相对密度;n为土壤孔隙度;e为沉降量,m;D为管径,m。
沉降与开始冲刷临界流速的关系曲线如图3所示。
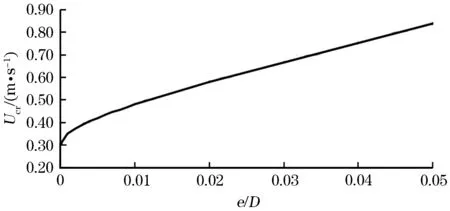
图3 恒定流条件下冲刷的开始
3 固定管道的平衡冲刷深度
随着时间的推移,海床的几何形状和冲刷深度最终将发展到一个平衡阶段,在这个阶段,海床剪应力将使海床发生非正常的运动。与这一完全发展阶段相对应的冲刷深度称为平衡冲刷深度。平衡冲刷深度必须经过一段时间才会达到,这段时间称为冲刷时间。
在恒定流的情况下,冲刷深度已经被广泛研究,Kjeldsen等在受控的海床条件下进行了冲刷实验,得出平衡冲刷深度可以用以下关系表示[5]:
(2)
Bijker和Leeuwestein对该表达式进行了改进,并考虑了砂粒大小的影响[6]:
(3)
式中:Se为平衡冲刷深度,m;v为恒定流速,m/s;d50为平均粒径,mm。
典型的管道平衡冲刷深度S/D随恒定流速v的变化如图4所示。
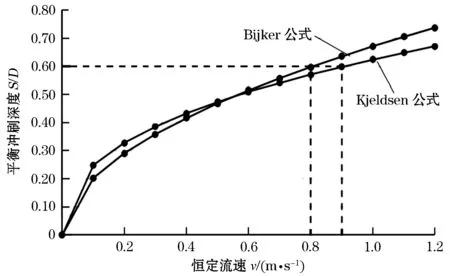
图4 平衡冲刷深度解析曲线
4 下降管道的平衡冲刷深度
实际上,管道会随着冲刷的进行而降低,在孤立冲刷的情况下,下降的管道通常会促进管道底部进一步冲刷。管道进入冲刷孔之前发生冲刷的程度取决于管道下降的速度和进一步冲刷速率的相互作用。研究发现,在大多数情况下,管道的下降会增加平衡冲刷深度。当管道下降到现有的冲刷孔中时,由于管道与海床之间的间隙减小,导致剪切应力增加,从而使平衡冲刷深度增加。由Cheng等[7]的研究可以看出,当近一半的管道处于海床高度以下(即e/D=0.5)时,海床平衡冲刷深度将达到最大。这时,流场发生了明显的变化,管道下方几乎没有流量。这个过渡点可以看作是持续冲刷和回填机制启动之间的过渡点。
Cheng等[7]的研究发现对于所有可能的管道下降率,在考虑管道降低的冲刷附加效应时,适用的冲刷基础应在0.65 冲刷时间
冲刷达到平衡的时间为
(4)
大多数研究都采用了p=1.0。Fredsoe等发现了一种归一化时间T*的方法[4],归一化时间是屏蔽参数的函数,表达式如下:
(5)
(6)
式中:T*为归一化时间;T为图5中实际时间,h;d为平均粒径d50,mm;θ为恒定流中屏蔽参数。
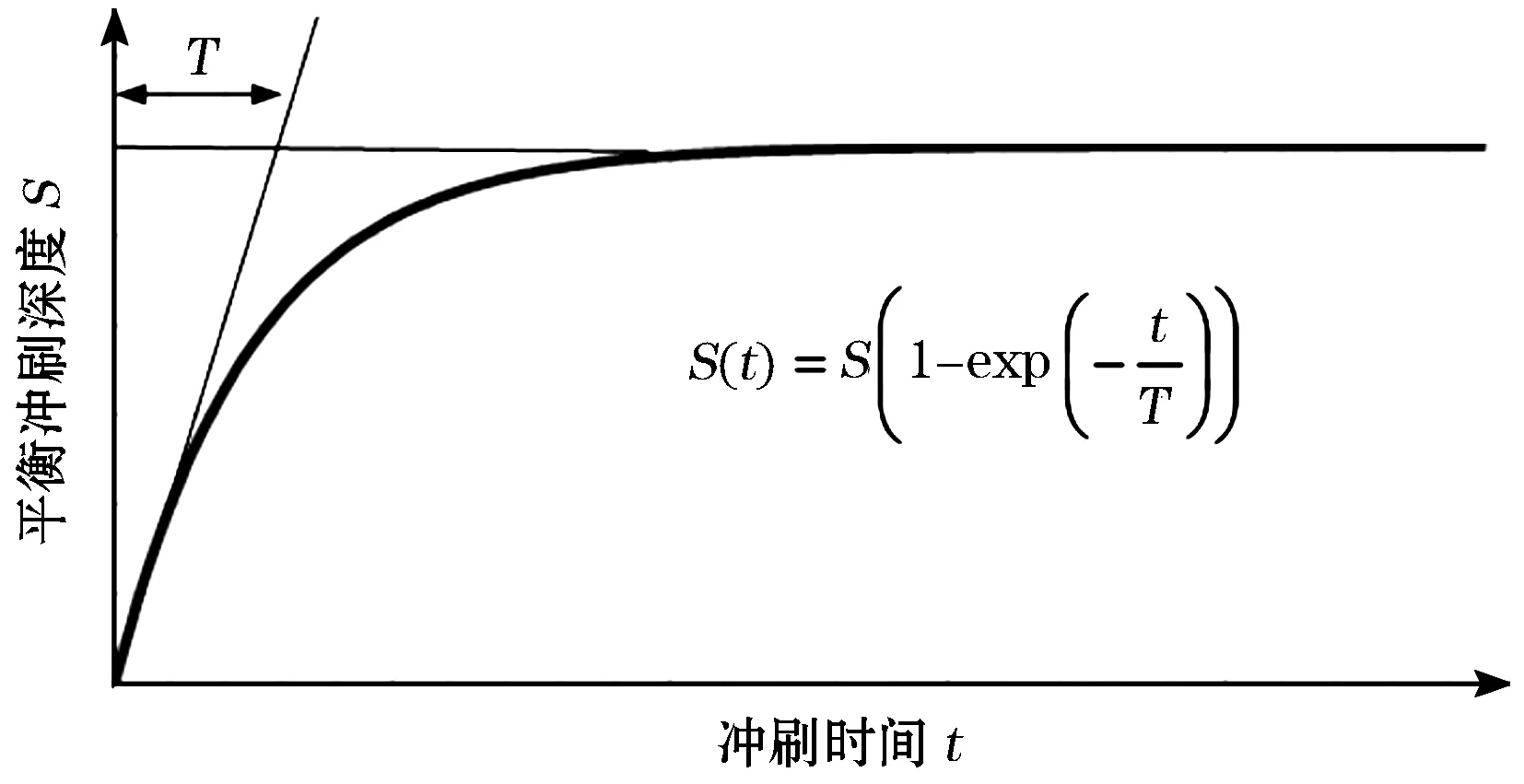
图5 平衡冲刷深度与冲刷时间的关系曲线
(7)
6 跨肩承载失效导致管道下降
相互冲刷作用的情况下,管道下降的机理是跨肩承载失效。排水条件下典型的非黏性沉积物,承载力适用以下关系式[8]:
(8)
式中:Qv为下降管道的垂向力,kN/m;γ′为土壤水下重,kN/m3;B为土壤承载宽度,m;Nγ、Nq均为土壤承载能力因子;dq为考虑深度影响的因数;Z0为深度影响的参考沉降量,m。
在实验中,出现了管道下降,这种情况发生在试验设施的侧面,并向内传播至管道中部,见图6。在某些临界点发生承载失效,管道因自身重量垂直沉入海床。
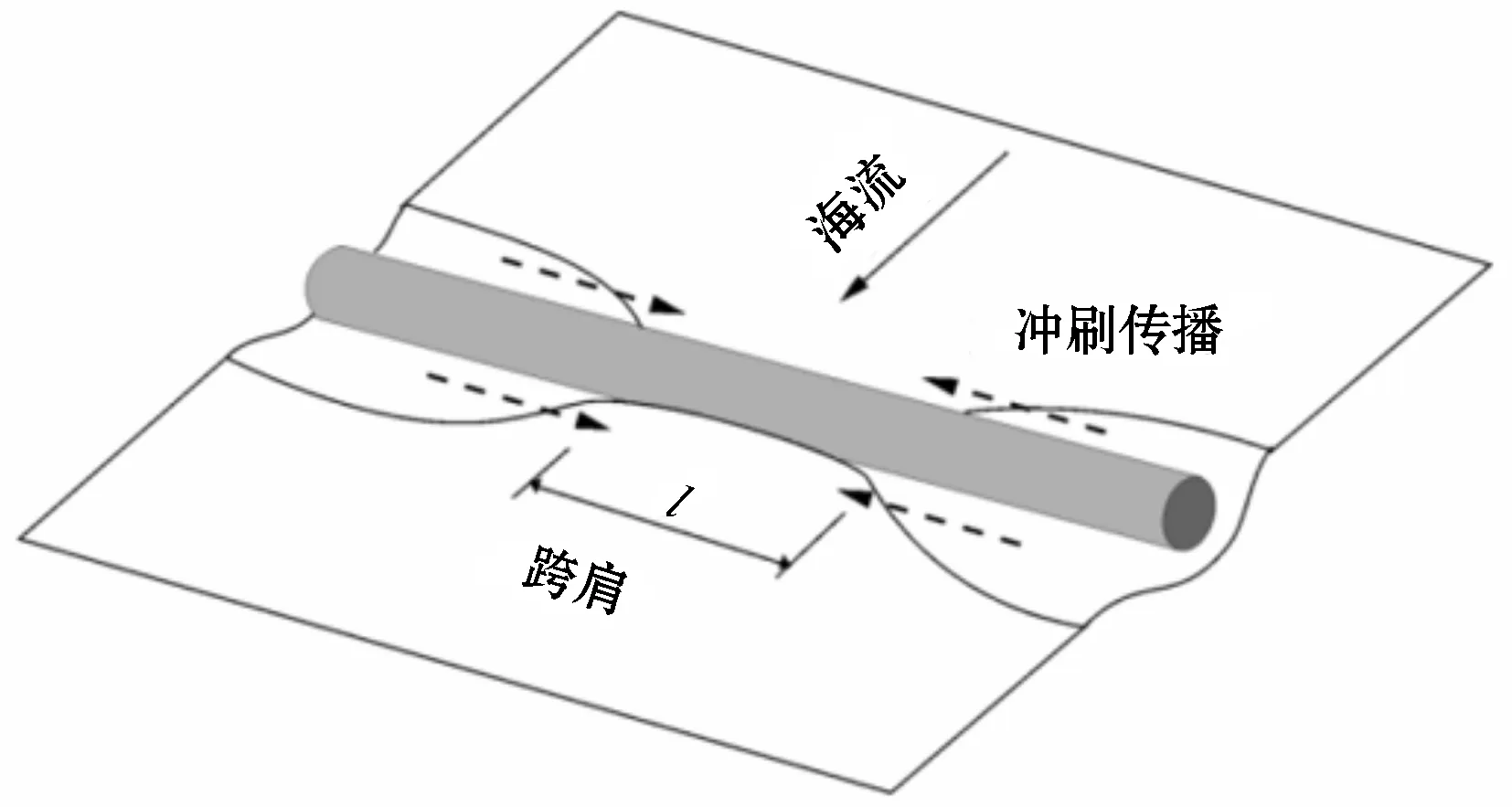
图6 冲刷传播减少悬跨肩长的实验示意图
管道在风暴的初始阶段经历了足够快的冲刷,基本被掩埋。增加初始沉降的效果是延迟冲刷的开始,这与Sumer等的发现是一致的[4]。管道的垂直位移不是平滑的,可能出现小的“跳跃”。这表明跨肩的阶段性“崩溃”,而不是连续的承载失效。这些跳跃对应的跨长与跨肩长之比是4∶1。此外,管道的下降很可能与管道的上游移动有关。这表明跨肩处的承载失效不是围绕管道轴线对称的。
7 研究实例
本文以南海某沙波区海底管道为例进行了冲刷分析,主要基础数据如表1所示。

表1 海底管道设计参数
海管总长26 km,水深范围144~286 m,输送介质密度953 kg/m3,土壤为中密实的细砂,内摩擦角Ф=20°。
表2中的结果是海底管道开始冲刷所需的恒定流速度。开始冲刷所需的流速与管道初始沉降深度密切相关,冲刷通常需要非常低的初始沉降来启动。对于超过3%的初始沉降,预计不会发生冲刷。
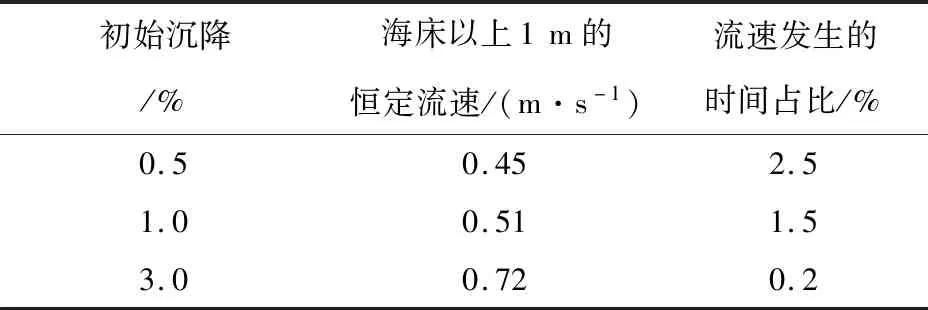
表2 海底管道开始冲刷的恒定流速
表3中的结果显示了根据Bijker和Leeuwestein[6]开发的公式计算出的固定管道在恒定流下的平衡冲刷深度。当预期的恒定流速全部发生时,固定管道的平衡冲刷深度大约为S/D=0.6。图7进一步描述了分析结果。
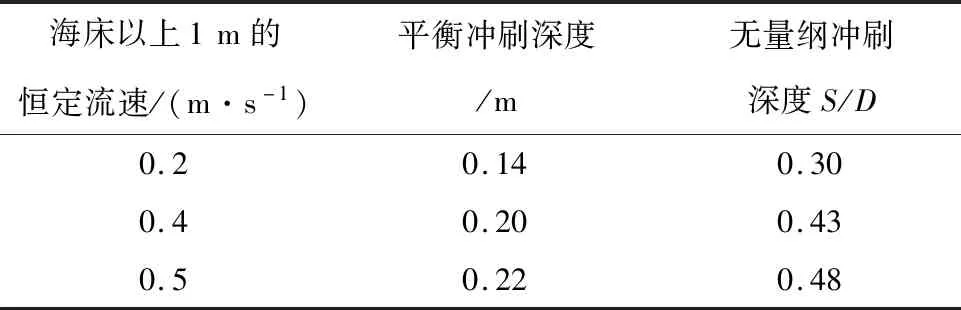
表3 海底管道的平衡冲刷深度

图7 海底管道在不同恒定流速下的平衡冲刷深度
表4中的结果显示了由于悬跨而下降的海底管道在恒定流速下的平衡冲刷深度预测。

表4 下降海底管道的平衡冲刷深度
计算结果表明,与固定管道相比,下降管道的平衡冲刷深度有相当大的增加。实际的平衡冲刷深度将受到管道下降速度、悬跨下垂距离和悬跨长度的限制,但将趋向于采用下降管道法预测的冲刷深度。
表5中的结果显示了采用Fredsoe等[4]的方法预测达到平衡冲刷深度的时间。
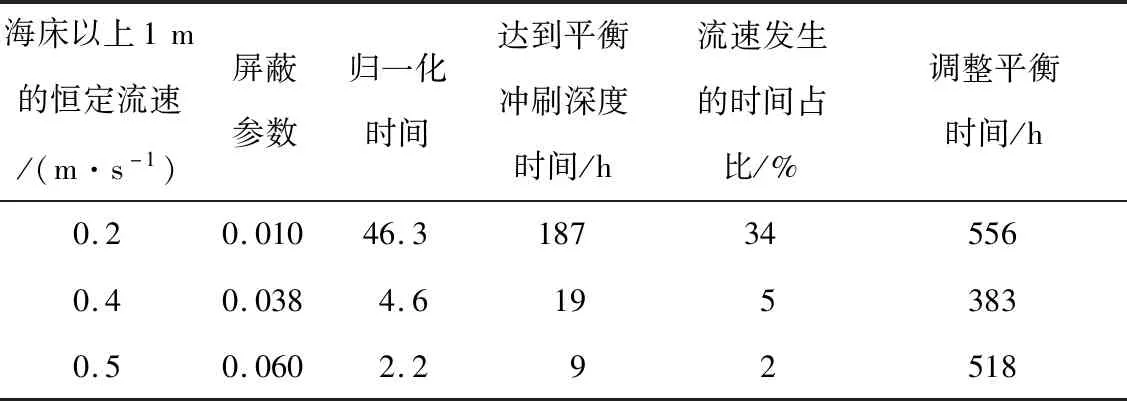
表5 海底管道达到平衡冲刷深度的时间
表6的结果显示了预计发生跨肩承载失效所需的跨肩比。例如,跨长与跨肩长度比为2∶1,表明在1 m长的跨肩上,跨长超过2 m将发生承载失效。该方法根据DNVGL-RP-F114[8]中给出的公式。在跨肩处管道埋设50%的基础上,全管径对承载力有贡献。根据承载力系数的取值范围,给出了相应的上下限。
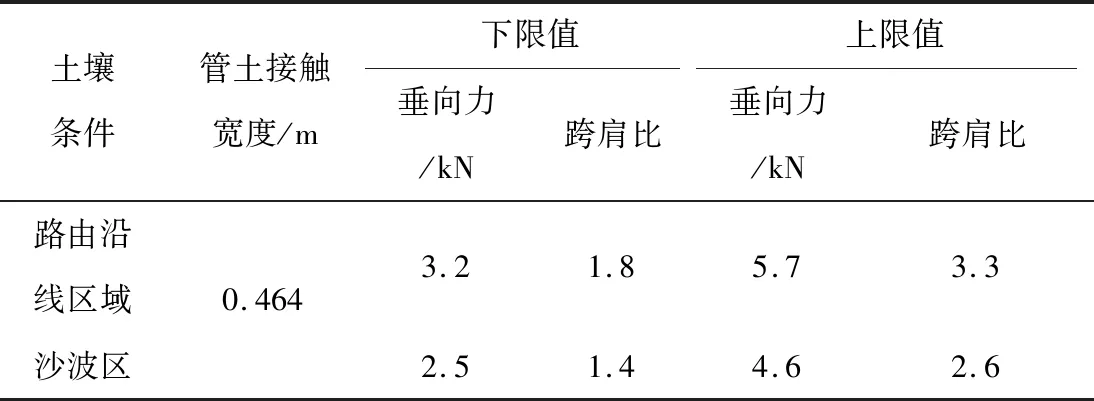
表6 预计发生跨肩承载失效所需的跨肩比
8 结论
冲刷行为是由周边的海洋条件主导的,如1年重现期的环境条件。在极端风暴,如10年一遇或100年一遇环境条件中,海床会发生显著的移动。在这种极端的情况下,是不能预测海底冲刷情况的。根据理论研究和工程实例的分析,可以得到如下结论:
(1)冲刷开始时需要非常低的嵌入量(如<1%)。沙土中,冲刷预计会发生在所有位置,除非有足够大的管道嵌入,冲刷不能启动。因为沙波和波纹贯穿了大部分海底管道路由,造成较多自由悬跨。这些影响将远超过铺设过程中发生的铺设嵌入效应(>3%)。预计约0.2 m/s的环境速度将足以使冲刷发生在这些自由悬跨的肩部,而且在海底管道整个操作期能同时发生孤立冲刷和相互作用冲刷。
(2)冲刷深度预计在0.6D~1.1D范围内。0.6D是固定管道仅在当前条件下的确定值,而1.1D是考虑管道自由悬跨下降率时的预测上限。对于实际下降管道的冲刷,埋深可达0.8D,甚至可能超过1D。
(3)时间的预测只适用于在特定位置已经开始的冲刷,且当前流速需持续不变,直至达到平衡深度,而这在实际中是不可能的。不同流速对调整平衡时间的影响不明显,说明冲刷时间整体量级与流速的关系不大。
(4)通过对具有多个冲刷位置相互作用的管道实例的计算表明,跨肩土壤承载失效将会发生的跨肩比在1.4∶1~3.3∶1的范围内。