食品包装热杀菌过程模型的建立及仿真研究进展

侯皓然，马淑凤，王利强

（江南大学机械工程学院 江苏省食品先进制造装备技术重点实验室 江苏无锡 214122）

热处理是食品包装工业化生产中维持产品品质稳定，延长货架期的有效手段。食品热处理技术主要包括干燥、杀菌。在杀菌方面，热处理过程可以杀灭包装内食品中的微生物，而同时也破坏了食品中的营养物质，导致营养物质降解，脂肪氧化分解等。随着计算机模拟技术的不断进步，越来越多研究者借助相关模型反映食品的热杀菌过程，并通过试验进行可靠性验证。在建模过程中，需考虑食品固有特性，加工过程中的多物理场耦合，以及包装、加热设备等介质特性，从而确保食品安全和食品营养、感官以及成本之间的平衡。本文从食品包装角度，综述食品传统热杀菌技术在计算机模拟与仿真方面的相关研究，主要关注热交换过程中，食品包装形式对内容物温度场分布、产品品质和微生物致死率的影响，为减少食品过度热杀菌提供理论支持，同时也为食品安全提供参考性指标。

1 传热过程控制方程

早期研究使用近似解析经验方法分析包装内部传导、自然对流的影响，例如合并固-液悬浮液有效扩散系数，将热阻限制于边界层等。这些研究很好的揭示了流体流动及传热情况，然而由于试验研究相对繁琐，这些测试所涉及的传感设备会产生较大误差，同时也会对内部食品造成污染，阻碍相关研究进展[1]。随着数值模拟技术的不断发展，结合计算机模拟仿真，对于复杂包装体系内的温度场分布以及其它相关数据可以得到更好的呈现。

1.1 Navier-Stokes 方程

相关传热过程中所涉及的数学模型主要与3位科学家有关，欧拉方程表征了牛顿流体的流动形式，也就是常见的质量、动量和能量守恒方程[2]。另外就是法国科学家Navier 和爱尔兰科学家Stokes 将动量守恒、动量通量本构方程以及不可压缩牛顿流体的质量守恒相结合得到Navier-Stokes 方程，针对牛顿流体而言，相关方程可简化如下：

式（1）是连续性方程，表示不可压缩流的流入质量与流出质量守恒；描述物质流变行为的连续性方程有很多，包括牛顿模型、能量定律模型、Bingham 模型、Bulkley 模型，其中能量定律模型使用最多[3]；式（2）是基于牛顿第二定律的动量守恒方程。对于一些具有非牛顿特征的食品而言，剪切力对热物性有着很大的影响，然而有相关研究认为在某些低速情况下，非牛顿流体可视为牛顿流体[4]，近些年也有许多关于非牛顿物质热交换模型方面的研究。Navier-Stokes 方程是食品传热传质建模的基础，通过方程求解可描述相关流体在热交换过程中速度场和压力场的变化，而速度和压力的变化会影响包装内温度场分布。

1.2 传热方程

用温度描述能量守恒，通过焓与温度和压力的关系表征，其中Cp为恒压热容，β 为体积膨胀系数，调用连续性方程得到温度方程：

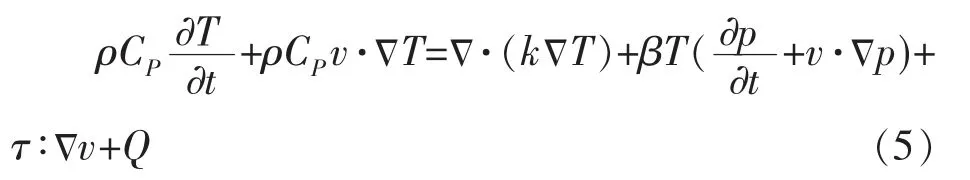
对于理想气体βT 项等于1，不可压缩流体的压力功项为零，大多数工程应用中，系统内没有明显压力变化，或马赫数远小于1，这时的压力功项也可以忽略，其简化方程为：

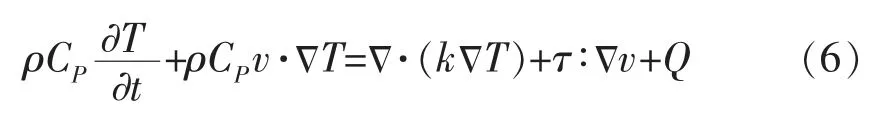
如果物质具有非牛顿属性，剪切速率非常高，需要考虑黏性加热问题，然而对于大多数情况而言，黏性加热可以忽略不计。

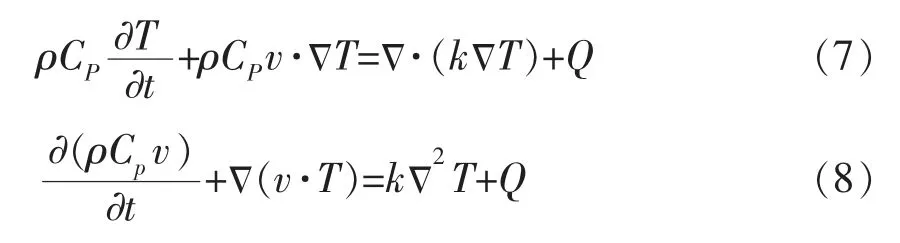
针对固体结构，在传热过程中模型在固液界面会进行持续的热交换，具有各向同性的固体热交换傅里叶方程为（9），该方程去掉了液体系统中温度对流混合项。

在使用数值方法实现方程时，不同的守恒方程并不等效。相关研究基于有限体积法，同时求解守恒形式的总焓输运方程，可以实现总能量守恒，然而利用总焓变求解容易发生数值振荡，降低求解结果精度，而利用温度方程建立总能量守恒，适用于有限元法，求解过程会更稳定，结果的精确度也较高。

设置相关材料热物性参数时，相关物质的密度与其所处的热力学状态有关，如温度和压力。热传导模型会得到相应物质材料的温度、水浓度和流体速度的变化曲线，这些曲线是传热过程中密度变化的函数。由于浮力产生的密度变化有2 个相关的模型，如下表1所示。

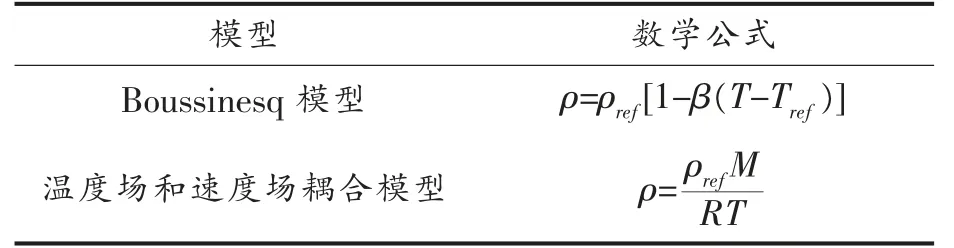
表1 密度变化模型Table 1 The model of density change

Boussinesq 模型假设温度与密度之间存在线性关系，其它相关特性恒定不变，由于该模型仅适用于单一液体成分，后面Taylor 提出相应的扩展理论，可以研究多种混合液体的变化。当温度变化较大时，会导致Boussinesq 模型的求解精度下降。因此提出温度场和速度场耦合模型，密度的变化与温度和组成成分有关，可以通过借助理想气体方程来表示密度差，该模型可以对弱可压缩物质建模，对于较小压力变化的情况也同样具有适用性。

1.3 边界条件与无因次数

设置适合于模型的边界条件，对于确定系统内的通量条件至关重要。为了保证温度分布的准确性，需要确定系统中加热食品与包装之间的对流传热系数。传热系数的确定可以通过优化方法和基于能量平衡求解的热交换数学模型得到。食品表面关于热量传递的边界条件数学模型[5]主要有Dirichlet 模型、Neumann 模型、Robin 模型，方程如下：

在建立包装食品传热过程模型时，边界条件必须与过程的相关物理参数精确匹配，由于涉及到食品品质机理相关的指标，有些试验过程复杂，难以直接获得或者难以获得大量可靠的试验数据，从而导致某些食品特性的不确定性。为解决这一问题，相关研究针对传热系数与食品及热过程变量关系建立预测模型，其中无量纲参数广泛用于传热系数问题的求解。

在热过程中，无量纲参数是输入变量和输出变量之间的联系，可以有效提高大试验量的运算速度，用于模型热过程中时间温度曲线相关问题，对不同热过程条件下的传热系数进行预测，确定传热过程中自然对流与强制对流之间比重关系；还可以在不考虑流体黏度和容器形状的情况下，快速粗略估计出所需的杀菌时间。常用于建立不同热过程条件与系统变量间联系的无量纲数主要有：Reynolds's 数、Nusselt 数、Biot 数、Prandtl 数、Grashoff 数等[6]。分析包装内液体的传热时，Fourier数表征最慢加热区（SHZ）的瞬时热扩散；液体的热扩散率还可以用Nusselt 数表征，是通过边界处对流和传导之比，解释杀菌过程中广义自然对流的影响[7]。

定义模型方程所依据的原理是根据守恒定律来定义用于产生通量的关系，需要在不同条件下反复求解给定系统的方程，然后研究计算结果，从而了解系统中的传递现象。

2 模拟热杀菌过程中的误差分析

许多计算机模拟软件中都包括计算流体力学（CFD） 模块，CFD 技术基于数值解析法可预测三维几何域中的传热机制。在食品包装领域，可用于分析包装内环境的热交换现象，明确SHZ 的位置，计算该区域杀菌过程时间，解释产品温度分布不均匀的现象。该技术对于保证产品质量安全，减少品质损失方面有着重要贡献。随着计算机模拟技术的不断进步，模拟过程可实现多物理场耦合，使模拟过程不断接近真实试验情况，试验对象也从单一模型扩展到整个环境系统研究，节约试验操作过程中大量的时间成本，减少环境误差。

在模拟传热分析过程中，主要涉及创建几何图形，将其划分为元素，离散化控制方程式以及使用合适的数值方案求解等，从大量关于食品包装的传热模拟研究中总结发现，影响模拟过程计算精度的主要因素有以下几个方面。

2.1 几何模型建立

对于一些大规模模拟仿真运算，由于几何模型较复杂，仿真历程所涉及的数据量较大，使得模型计算时间较长。对于一些几何较规则的模型，通常采用二维轴对称的方式进行简化，以达到缩短计算时间的目的。Lee 等[8]建立轴对称几何模型，通过试验测量沿着中心线上4 个不同位置的温度，以验证模拟结果的有效性。冷点位置温度可以得到F 值，以表征杀菌的有效性，然而由于包装内部自然对流的影响，致使冷点位置不断变化，导致无法测定杀菌强度，该研究对整个几何水平和垂直方向进行区域划分，将F 值最低的区域定义为最慢加热区（SHZ），观察整个杀菌过程SHZ 的温度分布，得到产品热杀菌温度变化规律。通过精细SHZ 大小，可以达到表征“冷点”温度变化的作用。在传热过程中，当1 个方向的尺寸远远大于另外2 个方向的尺寸时，可以选择建立二维模型[9]，以在确保精度的前提下减少计算时间。例如：薄膜、纸等包装材料，研究包含包装的传热过程中，可将其设置为二维薄层。然而对于一些不能轴对称简化的模型，仍需采用三维建模的方式，在一定程度上还可以提高其计算精度[10-11]。虽然在相关模拟研究中已广泛使用几何简化的方法以提升计算效率，但需要注意平衡求解结果误差与求解计算量之间的关系，选择合适的模型简化方案。

2.2 网格划分方案与时间步长的确定

网格的划分方式、尺寸大小影响模型求解精度和控制方程的空间离散。建模过程中的一般经验法则是：时间步长越小，网格细化程度越高，求解结果越精确。为了提高模型的精度，在定义网格时应该在一些尖端区域或特殊区域进行适当细化，以提高网格质量。偏斜角是通常用于衡量网格质量的指标，偏斜角的大小决定着边界扩散量是否可被计算。当偏斜角为0°时，表示两相邻元素中心矢量与两元素相邻界面正交，精度最佳；当偏斜角≥90°时，表示误差较大。然而有案例发现，有时网格细化程度高并不总能获得更高的精度，Boz等[12]研究发现，由于依赖计算域内液体的流动特征（如湍流、稳流）和求解参数（如时间步长、数值求解方案、网格细化结构），网格细化可能会导致计算结果的精确度降低。网格细化对温度的影响显著，在求解温度分布时会失去精度，即使缩小时间步长也不会带来相应的改善。网格过度细化在模拟初期会产生温度波动，从而破坏模拟结果。面对这一现象，Breuer 认为由于物理现象和数值影响不独立，预期模型和离散化误差在粗网格划分过程中会相互抵消[13]；另外一个解释来自于Druzˇeta等[14]的研究，由于处在CFL 环境下，细网格会使计算误差更快速的累计。

根据目前主要的研究发现，越来越多的研究者划分模型使用非结构化网格。非结构化网格是指采用多种形状的混合网格，从而增加网格形状与边界的匹配度[15]。研究发现，对温度和速度变化较小的区域进行细化网格划分，对结果的精度并没有很大的提升，仅延长了计算时间。Rabiey 等[16]在边界处使用较小的网格时，发现边界附近出现较大的速度和温度梯度。非结构化网格可在保证求解精度的前提下，对复杂的几何体进行自动离散。Habashi[17]在对边界处和几何主体进行网格划分时发现，在边界附近使用四边形或六面体网格时，边界层吻合程度较好，而几何主体区域可采用三角形和四面体结构，在保证精度的同时使求解更快收敛。

模型中时间步长的设置需要根据数值方案的求解稳定性、解决方案的时间精度和计算时间效率之间进行平衡。对于较复杂的数值计算而言，通常根据无量纲数Courant 来确定时间步长，保证计算过程稳定性。计算过程中为了获得合适的收敛水平Courant 数值应小于0.3，而Courant 数值与计算结果的准确性没有直接联系，采用粗网格划分的模型Courant 数值也可接近于0。Lespinard 研究发现时间步长与网格变化之间相互独立，可以根据模型建立适合的时间步长和网格划分方案[18]。

2.3 包装内部顶空对传热的影响

在实际工业生产过程中，无法做到密封包装内部空气完全消除，同时包装内部存在顶空气体也可以平衡包装内、外压力，使包装内存在一定真空度。对于这种情况，为了使模拟结果更加精确，相关研究者构建了包装内含顶空气体的模型，研究顶空气体对包装内温度场分布的影响。Erdogdu等[19]研究顶空与传热机制的关系，发现顶空的存在会加快包装内部的传热速率，这与一般经验认为的顶空气体影响传热的观点不符，仍需进一步研究证明。陈舒航等[20]发现顶空气体介质确实会加快传热速率，原因是由于顶空气体的比热与密度较小。同时，分析温度场云图还发现，气-液界面处由于水分蒸发，水蒸气未饱和时液面处温度较低。相比于固体包装产品，液体产品中内部顶空对传热速率的影响较大，原因解释为液体包装内部的传热主要涉及自然对流。Farazbakht 等[21]研究半刚性铝制包装下，内部顶空气体及浮力效应对传热的影响，通过模拟得到的温度场分布发现，SHZ并没有位于容器的几何中心，顶空气体的存在影响着SHZ 的位置和形状大小，然而有无顶空对SHZ 处的温度并没有太大影响。Tutar 等[22]模拟两相流在旋转杀菌模式下包装食品热杀菌过程，详细分析了罐旋转过程中顶空域形状及位置变化。增加旋转速率，顶空气泡离开罐壁，穿过液体，这加速了气-液两相流之间的混合，使温度场快速到达平衡状态。Ghani 等[23]研究发现旋转杀菌过程可使气-液两相流得到充分混合，SHZ 处的导热率是传统杀菌方式的4 倍。

3 基于传热相关模拟研究

在食品灭菌过程中，控制食品内部“冷点”或SHZ 的温度达到相应食品杀菌标准，同时尽量减少食品营养物质、品质的破坏至关重要。面对不同形式的物料，包装容器形状、摆放方式、内部食品成分比例及分布等都会影响相关温度场分布因素。

3.1 固体或黏性物料

通常认为固体 （或黏性较大的液体食品）的“冷点”位于食品的几何中心，数值求解时认为传热过程为纯热传导。然而对于一些不规则的食品几何模型，由于几何形状会影响传热率，因此“冷点”位置会受到模型几何尺寸的影响[24]。Kiziltas等[25]建立了固体含量较多的模型，巴氏杀菌（98℃）过程中分析温度云图发现，SHZ 位于几何中心与包装底部之间，固体成分的存在导致液体流动的速度场发生变化，在流动过程中与固体颗粒发生热交换。由于自然对流的传热现象，结合浮力作用，观察到温度场出现热分层现象，见图1。

图1 30 s 和300 s 时包装内的温度场分布图Fig.1 Temperature field distribution in the package at 30 s and 300 s

对于包装内容物为固体的产品，模拟杀菌过程通常忽略包装内部顶空的影响，因为固体食品热交换主要为食品内部热传导，顶空气体不影响食品内部“冷点”或SHZ 区域的导热。Shafiekhani等[26]研究半刚性铝塑包装容器（铝/聚丙烯PP 厚度125 μm） 在378 K 的环境温度下苹果泥的杀菌过程（T0=297.3 K），研究发现，顶空（高度为3 mm）水蒸气的传热系数较高，因此不会影响SHZ 的位置和形状。Vatankhah 等[27]模拟一种食品软包装的传统杀菌过程，同样得到该固体食品的SHZ 位置位于几何中心，选择该冷点位置测得F 值为23.8 min，优化模型得到最终F 值降为6.1 min 左右。

另一个影响固体类包装食品模拟结果精确度的因素是食品结构变化，如淀粉和蛋白质变性。Lee 等[28]建立了关于鱼肉蛋白的相关传热模型，结果发现考虑模型尺寸以及鳕鱼凝胶现象转变的模型具有更高的精度，如表2所示。

表2 不同包装形式（固体物料）的模拟案例Table 2 Model examples of different packaging forms （solid materials）

3.2 液体物料

由于液体物料具有流动性，较难确定SHZ 位置，液体流动提高热交换率从而传热过程加快。液体传热受自然对流的影响，而流体运动依赖于浮力的作用，因此可将能量方程中的温度与动量方程中的速度耦合。通过计算机模拟可以估计热杀菌所需时间，及热杀菌过程中的温度和速度场分布。

热杀菌过程中液体流动特征依赖于包装容器的形状和方向。Varma 等[31]研究非牛顿液体不同包装容器形状内SHZ 的位置变化，发现不同包装形状以及摆放方向影响热杀菌过程效率。Lespinard等[32]发现水平方向放置的容器内液体可以实现更快的混合，SHZ 处升温更迅速，同时计算得到水平放置的杀菌时间节约47.2%，减少质量损失约45.5%。Borah 等[33]以杀菌时间和热渗透参数为指标，评价不同椭圆率以及不同方向的容器承装非牛顿流体时的传热效率，通过改进包装以提供更加优质的传热特性。为了确定包装内液体流动形式以及温度场分布变化规律，针对包装容器内液体杀菌过程模拟的相关研究还有很多，见表3。

表3 液体杀菌过程模拟的相关研究Table 3 Related research on simulation of liquid sterilization process

有研究发现在模拟过程中，产品热物性参数的符合程度影响模拟结果的准确性。Bhuvaneswari等[42]研究热物性参数对于模拟结果精确度的影响，确定巴氏杀菌中7 个不同区域的温度场变化，得到PU 值17 作为品质控制指标，并发现受自然对流和热处理时间的影响，SHZ 位于包装底部。

3.3 固-液混合系统

关于食品热杀菌模拟研究，对于固液混合成分的物料，一般认为内容物中的液体成分的传热形式主要为热对流，而固体成分主要为热传导[43]。相关模拟研究发现对于固液混合系统来说，包装内部固体成分的存在影响SHZ 位置分布、灭菌时间以及内部液体的流动。

对于固液混合的食品物料，关于SHZ 位置的相关研究发现，因为热阻主要位于固体成分中，所以SHZ 位置分布于固体食品内部而不是包装罐几何中心；固体成分的存在会导致流体运动受阻，SHZ 位置相较于单纯液体成分的产品会上移；同时包装内固体成分的比重较大时，SHZ 位置也会上移[44]。Ansorena 等[45]研究固液混合系统中的SHZ位置与液体浓度之间的关系，发现SHZ 位于包装中轴线上，随固体成分比重增加，冷点位置会沿中轴线下移；而Dimou 等[46]研究芦笋罐头发现整体温度场分布和包装内部流场会受到固体成分比重和空间排布的影响，而最慢加热区和冷却区不受其影响，并且发现由于热阻主要位于芦笋内，液体流速不影响芦笋内温度分布。

在自然对流加热过程中，关于热交换速率和对流换热系数的研究发现，内部固体成分排布对液体流动方式和热交换率有显著影响；传递函数系数与包装尺寸之间也存在相应关系，该关系可用于不同尺寸的食品包装内温度场的预测[41]。Carino-sarabia 等[47]求解70 ℃和85 ℃温度下，不同液体环境中不同食物的对流换热系数，并研究食品颗粒数量对该系数的影响。Dimou 等[48]对糖水桃罐头产品内，热杀菌过程中不同桃摆放方式下的温度变化、液体流动形式、微生物F 值分布以及临界点位置进行了模拟分析。Cordioli 等[49]研究水果沙拉产品，发现靠近“冷点”区域附近的F 值最低，同时由于包装内自然对流，顶部区域水果的F值高于底部区域。Padmavati 等[50]以菠萝罐头为研究对象，研究包装内固体形状变化对热交换的影响。结果发现固体表面积较大的产品，导热率更大，同时自然对流加快。

4 结语

由于食品热交换可以使用偏微分方程对包装内空间传递进行表征，而对于食品内部相关品质变化涉及的理化反应模型却往往忽略热交换问题，这就导致建立宏观传热传质与微观分子理化综合模型难度较大[51]；另一方面，目前包装食品相关杀菌技术朝着多物理场结合的方向发展，这也对食品仿真技术提出了更高的要求。在食品包装形式多样化仿真方面，相关软包装材料产品由于其具有不规则几何特性，边界条件和几何近似简化数学模型研究比较困难。相对应的模型构建和试验验证，以及关于包装形式和热杀菌工艺的改进仍需进一步深入、系统的研究。同时为了便于模拟技术的商业化应用[52-53]，相关研究人员可针对不同种类的产品，参考相关应用开发适合于产品的用户界面，满足食品热处理工业环境模拟和相关优化条件的需求[54]。