“画”出思维过程,提升几何直观能力
江苏省苏州新区枫桥实验小学 李 珍
江苏省苏州市相城第一实验小学 谈怿斌
《义务教育数学课程标准(2011版)》的总目标中指出:要帮助学生初步形成几何直观能力,发展形象思维与抽象思维。同时要让学生获得分析问题和解决问题的一些基本方法,体验解决问题方法的多样性,发展创新意识。几何直观主要是利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。从本质上说,几何直观,就是利用图形进行思维及展开想象的能力。然而在目前的苏教版小学数学教材中,专门针对画图策略的教学内容只有三年级下册第三单元《解决问题的策略》中的例2和四年级下册第五单元《解决问题的策略》中的例1、例2。如果仅在这两个单元的教学中教学画图的策略,对培养学生几何直观能力一定是远远不够的。因此,我认为,培养学生几何直观能力,应贯穿于整个小学阶段的数学教学中。
一、深入挖掘教材内容,循序渐进教学画图策略
仔细研读苏教版小学数学教材,我们不难发现,在各册教材的编排中都大量运用了情境图、实物图、符号图等图形素材,许多例题都在引导教师和学生运用画图的方法探究解决问题的方法。因此,我们应当认真梳理各册教材,深入挖掘教材中的资源,充分发挥这部分例题、习题利用图形描述和分析问题的价值,让学生在潜移默化中理解画图的意义。
经过梳理,我把苏教版小学数学教材中渗透教学画图策略的相关内容分类如下:
(一)实物图
小学生的认知水平属于皮亚杰所划分的儿童认知发展阶段的第三个阶段(7~12岁):具体运算阶段。具体运算思维一般还离不开具体事物的支持。因而,在苏教版小学数学教材中,尤其是低年级教材,大量运用了实物图。例如:一年级上册第一单元《数一数》,第五单元《认识10以内的数》。《数一数》是学生进入小学阶段的第一节数学课,对于每个学生的数学学习都具有十分重要的意义。同时初步渗透了一一对应思想和符号化思想。《认识10以内的数》单元中,例1在主题图下面依次呈现了实物图、数珠图、数字,目的是把数字与相应的数珠以及相应个数的物体联系起来,赋予数字具体的含义,从而让学生有意义地接受数学符号,逐渐形成数的概念。
(二)符号图
皮亚杰指出,“具体运算阶段”发展最典型的标志就是能够运用符号进行有逻辑的思考活动。因此,在实物图的基础之上,教材逐步抽象,适时采用圆点图、数珠图、符号图等,使学生进一步感受一一对应等数学思想,从而深入直观地理解“同样多”“多多少”“少多少”等数量关系,为后续解决问题建立丰富的表象和经验。例如:一年级上册第五单元《认识10以内的数》第25页“想想做做”第8题,第27页“想想做做”第9题,第69页“想想做做”第2题。教材有意识地从比较实物的多少,逐步抽象为比较符号的多少,进而通过画画填填,使学生初步学会用“画”的方式解决简单的计算问题。
(三)直条图
在一年级的学习中,学生对实物图、符号图已经积累了较为丰富的表象,并能借助画符号解决一些简单的计算问题。随着年龄的增长,学生的思维从形象思维逐步向抽象思维过渡。教材中的实物图、符号图也随之逐步抽象为直条图。例如:二年级上册《100以内的加法、减法(三)》第7页“想想做做”第2题。教材借助相差关系的问题逐步把实物图抽象为直条图,为进一步抽象成线段图做好了过渡和铺垫。
(四)线段图
线段图利用线段来描述和分析问题中的数量关系,是最常用的画图形式之一,用线段图来表示相差关系、倍比关系、行程问题等,可以把复杂的数学问题变得简单、形象,有利于探索解决问题的思路。线段图以其形象、直观的特点,在数学教学中广泛应用。注重让学生运用线段图来解决实际问题,可以有效提高学生的自我学习能力和创新能力,同时促进学生思维的发展。
三年级下册《解决问题的策略——画线段图》,是学生第一次正式学习画线段图解决问题。特级教师徐斌在教学中,设计了红花和蓝花之间倍数关系的实物图,然后过渡到正方形图,再逐渐演变为条形图,最后抽象成线段图。这一过程让形象到抽象的过程变得可视,使学生在不知不觉中对线段图有了本源性认识。为接下来进一步学习画线段图和分析数量关系做好了充分铺垫。
(五)示意图
在第一学段的学习中,学生已经积累了一定的看图、画图经验,如学习一个数是另一个数的几倍时,用画一画、圈一圈的方法理解“倍”的含义;学习一个数比另一个数多(少)几时,通过线段图理解求较大数和求较小数的方法;学习长方形、正方形的周长与面积时,也经常画图……但是还没有将画图上升到策略的高度来体会和感悟。随着课程内容的螺旋上升,学生面临的学习内容难度逐步加深,数量关系愈加复杂。此时,学生需要进一步借助几何直观把复杂的问题变得简单、直观。除了进一步运用线段图之外,平面示意图和立体示意图在解决相关实际问题时也发挥着重要作用。

(1)平面示意图
四年级下册《解决问题的策略》,除了进一步学习用线段图解决“和差问题”之外,重点学习画平面示意图解决有关图形面积增加或减少的实际问题。
梅山小学有一块长方形花圃,长8米。在修建校园时,花圃的长增加了3米,这样面积就增加了18平方米。原来花圃的面积是多少平方米?
仅仅从文字上看,这个问题很难解决,但通过画图,可以清晰地看出长增加与增加面积之间的关系,从而求出原来宽,再解决面积问题。
(2)立体示意图
六年级上册《长方体和正方体》这一单元,安排了如下思考题:一个长方体,如果高增加2厘米,就变成一个正方体。这时表面积比原来增加56平方厘米。原来长方体的体积是多少立方厘米?
仅看文字,很难真正理解题意。通过画图,引导学生观察图形,找出表面积比原来增加的部分是4个完全相同的侧面。因此,用增加的面积先除以4,得到每个侧面的面积。从图中还能清楚地看出高增加的2厘米是这个小长方形的宽。基于以上理解,可以轻松求出现在正方体的棱长,进而求得原来长方体的高。原来长方体的体积也就迎刃而解了。
借助画图,可以把抽象的数据变成直观的图形,从而更好地理解条件和问题之间的联系,便于直观分析各数量之间的关系,从而形成解决问题的思路。
从低年级的实物图、符号图、直条图,到中高年级的线段图、平面示意图、立体示意图,教材编排层层递进,逐步渗透。无论是基于学生思维发展的特点,还是从教材编排意图看,教师都应将“数形结合”思想贯穿于整个小学数学教学中。
二、着力培养画图意识,由易到难教学画图方法
画图能力的培养绝非一日之功,需要逐步渗透,让学生在循序渐进中掌握。
(一)培养学生良好的画图习惯
低年级是形成良好学习习惯的关键时期。因此,画图习惯的培养同样要从低年级开始。还是以一年级上册第一单元《数一数》为例。当学生在用画圆点的方式表示每一种物体的数量时,老师一定要强调圆点的画法,要求大小均匀、排列整齐。从小培养学生严谨、细致的画图习惯,为后续进一步学习画图策略奠定良好基础。按要求画正方形,不仅要求正方形大小合适、形状规整,更要强调一一对应的画法,渗透对应思想,为后续画线段图埋下伏笔。教师示范、同伴影响,都是培养学生良好画图习惯的有效方法。
(二)激发学生自主画图的意识
画图作为一种解决问题的有效策略,如果变成老师一厢情愿的“推销”,那么非但起不到帮助解题的作用,反而会成为学生的负担。因此,培养学生自主画图的意识是关键。教师在教学中要尽量使用图形分析问题、解释结果,通过画图使学生感受在分析问题、解决问题时图形的优势,让学生由被动的画图逐步形成主动用画图来解决问题的意识。在润物细无声的教育中爱上画图策略。
(三)加强画图方法的指导
画图能力的形成依赖于画图方法的娴熟掌握,因此,教师在教学中要注意引领学生归纳整理画图方法。
特级教师徐斌在执教四年级下册《解决问题的策略——画示意图》一课时。为了让学生更好地理解“长增加3米,从而面积增加18平方米”的含义,大胆放手,让学生尝试自己画图。学生一开始只把其中的一条长增加了3米,教师问:“现在面积增加了吗?”
“没有增加。”
题目里说长增加了3米,面积就增加了18平方米,哪里是面积增加的部分?
“现在面积增加了吗?”
学生感觉好像缺了什么,又补上长方形的宽。
只有老师有意识地引领和指导,学生的画图能力才会不断增强。
三、灵活运用画图策略,由浅入深提升数学思维
画图策略,可以让学生的思维走向更深、更远处,让学生的思维能力在春风化雨中提升。
(一)“画”抽象为直观
数学是一门抽象的学科。有些数学问题仅凭文字,学生理解起来比较困难。例如,五年级下册《因数和倍数》单元中,学生运用“最大公因数”知识解决如下问题时,如果没有图形的支撑,很难深入理解题意。
把一张长15厘米,宽9厘米的长方形纸(如图)裁成同样大的正方形,如果要求纸没有剩余,裁出的正方形边长最大是多少厘米?一共可以裁出多少个这样的正方形?(在图中画一画,再回答)借助图形,可以使学生更直观地理解问题,从而有效突破教学的难点。
清污水分离主要是把厂区内村民生活水及职工澡堂水汇集回收再处理复用,保证污水不外排;减少生产系统内补加清水量。
(二)“画”繁为简
正如华罗庚先生所说:“数缺形时少直观,形少数时难入微。”五年级下册第七单元“解决问题的策略——转化”中的例2,是一道分数连加算式。
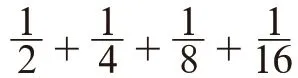
巧妙利用数形结合,可以将有些复杂的数学问题变得简单。这样借助画图策略,让学生在直观形象的图形中找到问题的突破口,同时也渗透了转化思想。
(三)“画”难为易
随着年级的升高,数学问题的综合性也越来越强。例如:在教学“圆柱和圆锥”的体积时,有时会和比的知识联系起来,如下图所示思考题,学生理解起来有一定难度。
一个圆锥和一个圆柱底面积相等,体积的比是1:6。如果圆锥的高是4.2厘米,圆柱的高是多少厘米?如果圆柱的高是4.2厘米,圆锥的高是多少厘米?
此时,可以借助画图,从最容易想到的“等底等高”的情况画起,先画一组“等底等高”的圆锥、圆柱,这时它们的体积比是1:3。此时只需引导学生思考,在底面积不变的情况下,怎样使圆柱的体积扩大为原来的2倍?借助图形,学生比较容易思考得出只要把圆柱的高扩大为原来的2倍,从图中就能清晰地看出,此时两者体积之比就是1:6了。此时圆锥和圆柱的高之间的关系从图中一目了然。
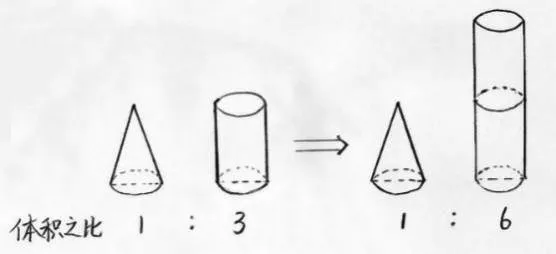
利用画图,原来难以理解的问题变得简明、直观,问题迎刃而解。
(四)“画”动为静
在推导图形计算公式时,常常需要用到转化的思想。例如,推导圆的面积公式、圆柱的体积公式等,新授过程中,教师通常会借助实物或多媒体进行动态演示。而在练习过程中,这样的推导过程不可能也没有条件每次都进行动态演示。此时,引导学生把“动态”的转化过程用“静态”的示意图画出来是很有必要的。
(五)“画”中有话
在解决问题的过程中,学生不仅要会画,更要学会“说”画。将图形中的数量关系用数学语言表达出来,从而更加有效地提升学生的思维能力。学生在经历了画图的过程后,教师在此基础上进一步追问根据画好的图你能知道些什么?引导学生说出图中所表示的数量关系。在说的过程中一方面让学生进一步感受图形的直观,另一方面也理清了解题思路。进而感悟到画图在解决问题中的价值。
(六)“画”在心中
画图是解决问题的手段,而不是最终目的。学生熟练掌握画图策略后,在解决问题时图形便会自然浮现在脑海中,原来必须要画在纸上才能够看明白、想明白的图形,可以转而画在心中。徐特提炼为:无剑之境,无招之意,无名之实,无形之美。此时,画图的策略上升为模型思想,学生的空间观念、几何直观也便有了切实的提升。
当然,学生画图能力的培养,几何直观能力的提升,不是一朝一夕的事。教师在教学过程中要遵循循序渐进的原则,使学生逐步掌握“画图”的数学技能,逐渐形成主动运用画图策略帮助分析、思考问题的意识,从而提升学生几何直观能力,最终促进学生思维能力的发展。

