基于显式动力学有限元法的球鼻艏碰撞机理研究

王付鹏，张岳林

(1.91411部队，辽宁 大连 116041；2.同济大学 建筑工程系，上海 200092)

0 引言

船舶在服役过程中有可能受到各种灾害的威胁，其中有一些是不可避免的，如腐蚀与疲劳，而有一些是意外事件，如碰撞、搁浅、爆炸与冲击。不考虑意外事件的船体结构设计可分为许用应力设计和极限状态设计(Ultimate Limit State, ULS)，而考虑意外事件的设计称为意外极限状态设计(Accidental Limit State, ALS)。虽然意外事件发生概率低，但其造成的损伤却往往比常规载荷大得多，所以，在船体结构设计中应高度重视ALS。

为了支撑近海活动乃至产品的进出口，海洋结构和船舶变得必不可少，船舶安全和结构愈来愈受到重视。在航行和抛锚模式中，船舶可能遭受各种载荷，这些载荷必须被抵抗以保证船舶完成目标和船员、乘客、货物和船舶自身的安全。这些分析包括结构的应力和强度。对于这种分析，必须知道载荷信息，而且初始结构的构件尺寸设计必须合适。结构分析的输出称为结构响应，它被定义为应力、变形和强度等术语。然后，估计的响应与设计标准对比。然而，其他不能被抵抗的载荷可能会突然出现，这些载荷会导致重大的船舶和环境事故。碰撞产生突发载荷，这些载荷经常联系到消极结果，造成严重的人员伤亡和经济损失。在其他碰撞实例中，环境损害可能会产生，如油从舱容器中泄漏。除了作为意外载荷外，碰撞还被分类为一种冲击现象，它的发生是高度非线性的。根据材料、结构等不同的影响，碰撞的形式是多种多样的。

由于碰撞模型的高度非线性，很难使用解析法对碰撞过程进行计算，为此，本文基于非线性有限元，以某球鼻艏为研究对象，建立了其与刚体碰撞的有限元模型，对碰撞过程的损伤变形、接触力和能量变化进行了分析，同时研究了材料应变率对碰撞过程的影响。

1 非线性动力学分析流程

非线性动力学分析流程主要包括建模、赋予材料属性、施加载荷与边界条件、划分网格、定义分析步、提交作业分析和后处理，见图1。

2 研究对象

用CAD软件Catia建立船首几何模型，并导入CAE软件Abaqus中。几何模型见图2，模型材料为一种铝合金，其应力-应变关系见图3。网格划分见图4。网格类型为S4R(4节点双曲线薄/厚壳，缩减积分，沙漏控制，有限薄膜应变)。船首结构单元总数为1 387，方板单元总数为400。

船外板的厚度为10 mm，初速度为10 m/s，撞向完全固定的方钢板。在实际碰撞过程中，由于被撞对象刚度较大，如冰山、海岸或船只，且考虑惯性的作用，所以可将被撞物建模为刚体。方板中心与球鼻艏端部的初始相对距离为360 mm，约束方钢板3个方向的自由度(见图5)。创建一个0.04 s显示动态分析步，每0.5 ms输出1次结果数据，球鼻艏与方板的接触属性无摩擦。

图1 非线性动力学分析流程

V—垂直方向；H—水平方向；O—重合。

图3 材料的应力-应变曲线

图4 网格的划分

图5 载荷和边界条件的施加

3 碰撞过程及结果分析

3.1 损伤变形分析

碰撞过程从34.4 ms开始，经计算：

(1)球鼻艏与四边固支方钢板之间的变形和结构毁伤产生在碰撞的局部区域，符合圣维南原理。

(2)在四边固支方钢板的压缩作用下，球鼻艏碰撞区的铝合金材料达到屈服强度，结构发生变形。在初始时刻，弯曲变形较小。随着时间的增加，球鼻艏的损伤变形越来越严重，损伤面积也越来越大。

(3)碰撞后，船体板在撞击下下沉，船首侧板发生不同程度的屈曲变形。

(4)碰撞后，船首发生倾覆和翘曲，使得仿真计算的船首损伤程度小于实际情况。翻倒翘曲的原因主要有2个：一是为了提高计算效率，球鼻艏与四边固支方钢板之间接触的法向行为设置了无摩擦，实际上2个接触体之间有一定的动摩擦系数，从而限制两者之间的相对运动；二是全船质量应沿船长方向分布，而本文只建立了船首的局部模型，使全船质量集中分布在船首的局部区域。解决这一问题的主要方式有2种：一是建立整船的有限元模型，但这种方法在计算效率上显然是不经济的；另一个简单的方式使通过施加力学边界条件来实现船首翻转的人为约束。

(5)在仿真中，冲击板是一个理想的刚体，但实际情况是一定的弹塑性变形，这使得模拟的变形和失效大于实际情况。

3.2 相互作用力

为了观察的方便性，选取被撞方钢板的中心点作为参考点，作为碰撞力的输出对象，相互作用力为球鼻艏顶端的反作用力。方钢板中心点碰撞力的时变曲线见图6，球鼻艏中心点的时变等效应力(米塞斯应力)曲线见图7。从碰撞过程开始(第0.5 ms)到第35 ms的应力-时间曲线几乎是一条直线，说明此时球鼻艏材料处于弹性变形阶段。到第35 ms时，球鼻艏的等效应力为154.31 MPa，达到材料的屈服强度，球鼻艏材料进入塑性工作状态。球鼻艏发生塑性屈曲，应力-时间曲线呈高度非线性。从接触力-时间曲线可以看出，方板中心的接触力开始减小，说明球鼻艏开始滚动，球鼻艏中心逐渐离开方板。从球鼻艏中心位移随时间变化的曲线可以看出，在38 ms时，球鼻艏中心点完全离开方形板，接触力消失，但从图7可以看出，此时球鼻艏的中心应力并没有开始减小，说明球鼻艏材料具有不可恢复的塑性应变。

图6 接触力-时间曲线

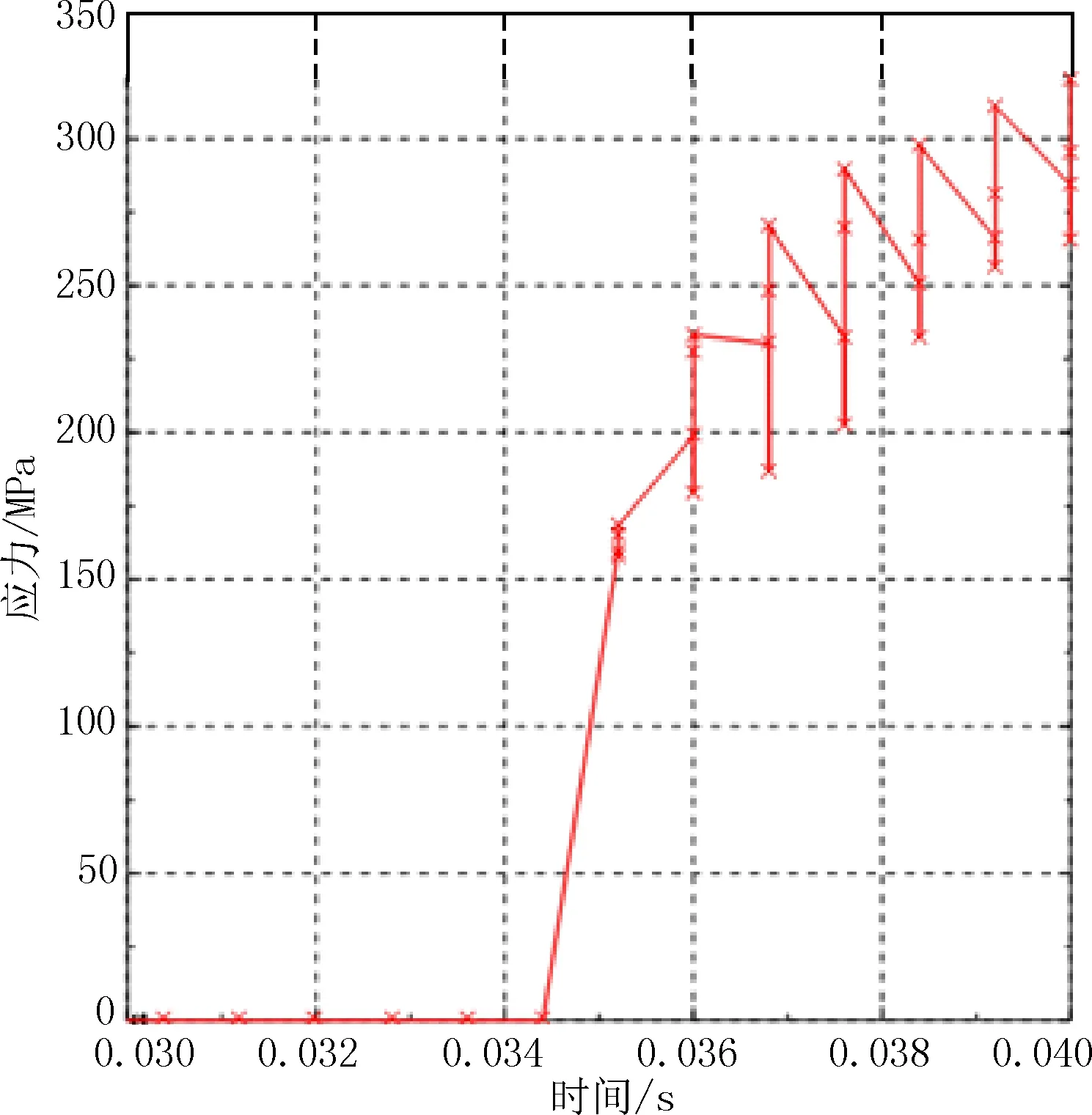
图7 应力-时间曲线

3.3 能量变化

图8展示了铝合金球鼻艏在碰撞过程中吸收的总能量和船舶运动时的动能损失，其中ALLAE是伪应变能。当伪应变能小于内能的5%时，沙漏模型对计算结果影响不大。由图8可知，最大伪应变能约为2.5×10J，最大内能约为2.3×10J，伪应变能约占内能的1%，证明了分析的有效性。

图8 能量-时间曲线

从图8可以看出，在船首与固定板的碰撞过程中，随着时间的推移，由于船首构件变形较大，变形需要吸收能量，从而使船体的变形能量增大。所有增加的能量都来自船体的初始动能，因此船体变形能单调增加，动能单调下降。从图8可以看出，碰撞结束时，内能达到最大值，应变能达到最大值。结合图7，此时应力和应变达到了最大。

4 材料率相关对碰撞过程的影响

一些材料表明屈服应力随着应变率的增加而增加。由于加载速率较高，应变率相关性可能非常重要。利用率相关特性的定义，由动屈服应力与静屈服应力之比给出等效塑性应变率，计算公式为

有无率相关情况下球鼻艏塑性应变能见图9。

图9 有无率相关情况下球鼻艏塑性应变能

由图9可以看出，不考虑率相关

效应时，整个碰撞过程的塑性应变能为1.8×10J；考虑率相关效应后，塑性应变能约为2.7×10J，比不考虑率相关时增大了约50%，说明考虑率相关效应后随着应变速率的增加，铝合金材料球鼻艏存在增塑效应。

有无率相关情况下球鼻艏中心点位移历史见图10。由图10可知，由于离开方板前球鼻艏中心点与方板贴合，有无率相关情况下球鼻艏中心点位移曲线几乎重合，这种塑性硬化效应在第38 ms球鼻艏中心点离开方板后自由振动时开始在宏观上微弱的表现出来，也就是说考虑率相关效应后，碰撞过程机理发生变化，但最终的毁伤变形结果几乎是一致的。

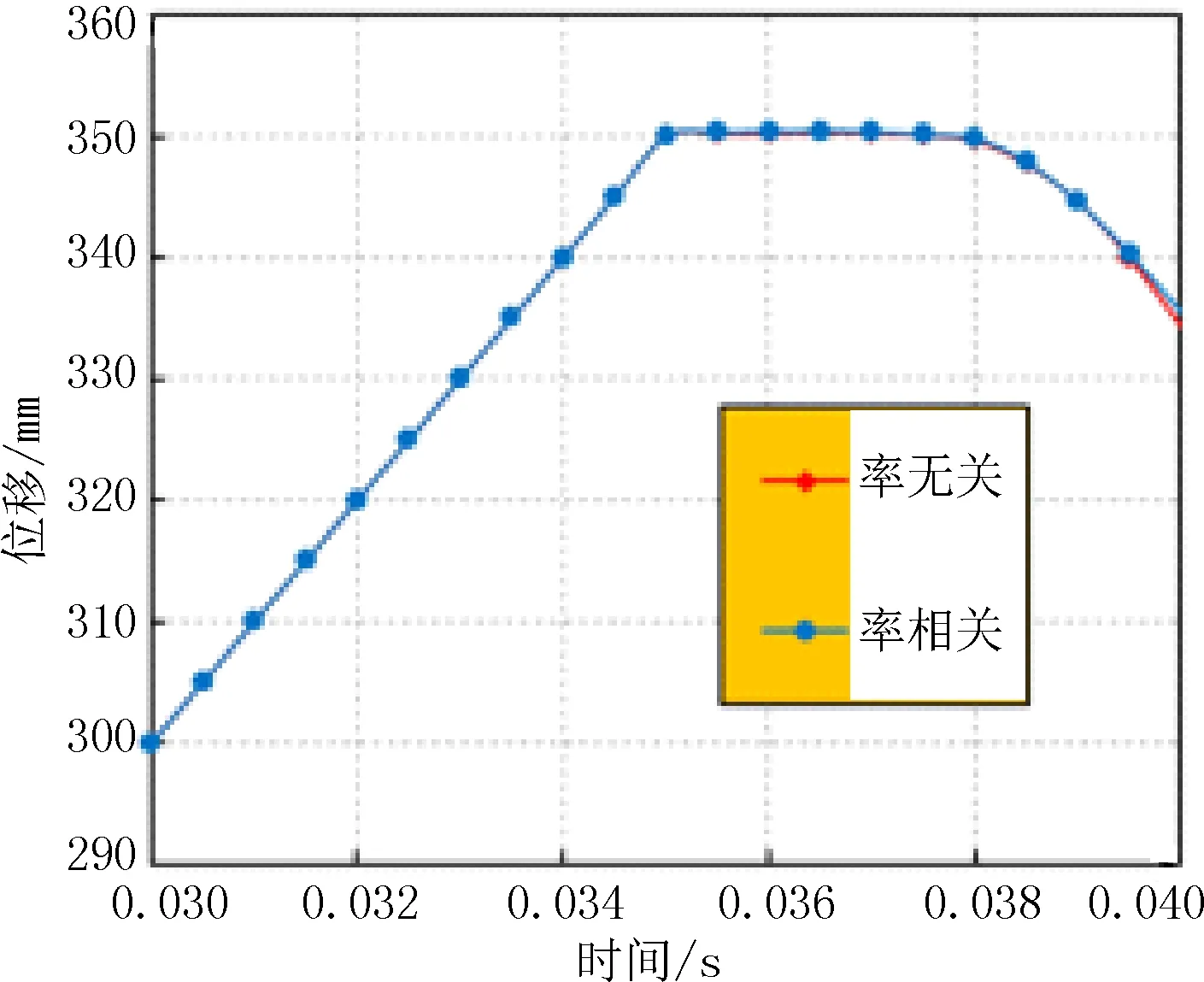
图10 有无率相关情况下球鼻艏中心点位移历史

5 结论

(1)球鼻艏与方板碰撞时，损伤和变形主要发生在与方板的接触部位，而舷侧板等部位只发生轻微变形。

(2)球鼻艏与方板碰撞时，大部分动能转化为球鼻艏结构的内能，少数转化为应变能。

(3)考虑材料率相关效应后，整个碰撞过程的塑性应变能比不考虑率相关时增大了约50%。