融合GMS的ORB特征点提取与匹配算法
潘 峰,沈建新,秦 顺,林 鑫
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引 言
特征点提取与匹配技术是图像处理技术中的一个很重要的分支,对于目标检测和同时定位与建图(simultaneous localization and mapping,SLAM)等领域而言尤为关键[1]。现如今,特征点提取和匹配的算法种类及其变形数量很多。经典的算法包括将有方向的加速角点提取(features from accelerated segment test,FAST)[2]和带旋转的二进制独立基本特征(binary robust independent elementary features,BRIEF)[3]融合在一起的ORB算法[4](oriented FAST and rotated BRIEF,ORB)、基于尺度不变特征的SIFT算法[5,6](scale-invariant feature transform,SIFT)、基于加速稳健特征的SURF算法[7](speeded up robust features,SURF)以及Harris Corner Detector[8]。这些算法在处理特定图像变换时凸显出了各自的优势。ORB算法的一个特点就是检测速度快,可用于实时图像特征点提取与匹配,该算法中采用了旋转不变性原则以此提高提取与匹配的准确性。
BRISK算法[9]、KAZE算法[10]以及AKAZE算法[11]也是极其优秀的算法,这些算法对旋转和尺度变换都具有不变性,算法具有极好的鲁棒性。
针对一些优秀的算法,国内的许多学者[12-14]也做了相关的算法变形,这些算法不仅拥有原算法的优点,还对原算法的一些不足进行了改进,让算法性能显得更加优秀。
由于传统ORB算法提取的特征点分布不均匀,使得图像有些区域提取不到特征点,从而浪费了图像上的大量有用信息,同时在匹配的过程中利用运动平滑性约束剔除误匹配的方法会导致仍然存在一些误匹配,因此先利用四叉树原理对图像分区域提取ORB特征点,在提取完特征点之后使用GMS匹配方法[15]将运动平滑性约束替换成基于网格的剔除误匹配的统计量,以此来剔除误匹配,最终得到分布比较均匀且正确的匹配特征点对。
1 ORB算法分区域提取特征点
1.1 FAST角点检测算法
ORB算法是目前特征点提取匹配中用的比较多的算法之一,该算法由Oriented FAST关键点和Steer BRIEF描述子两部分组成。
FAST算法是一种二维图像的特征检测算法,它可以迅速地找出一张灰度图片中潜在的特征点,而且速度飞快。
具体实现步骤如下:①以目标像素点p为中心,取半径r上M个领域像素点。②分别计算取得像素点与目标像素点p的灰度之差的绝对值。③利用计算得到的灰度差的绝对值与所设定的阈值进行比较,如果大于阈值,则该点为FAST角点。
对原始ORB算法的特征提取进行改进,提出oFAST(FAST keypoint orientation)算法,在快速提取特征点后,又定义了特征点的方向,实现特征点的旋转不变性。
1.1.1 粗提取
若判断选择的点是否是特征点,可以采取的方式是在该点周围以一定半径画圆,来判断这个圆里的点像素灰度大于圆心点灰度的数量是否大于某个阈值,若大于某个阈值,则说明圆心那一点为特征点,否则就不是特征点。FAST角点检测原理如图1所示。比较常用的是在圆心周围选取9个像素点的FAST-9和选取12个像素点的FAST-12。通常可以先按垂直方向的关系选取4个像素点,如果这个4个像素点中有2个的像素灰度比圆心灰度大,有2个像素灰度比圆心灰度小,那么圆心点不是特征点。

图1 FAST角点检测原理
1.1.2 筛选最优特征点
筛选出最优特征点的方法有很多,其中机器学习的方式比较常见。把特征点周围的像素点输入到ID3算法训练出来的决策树中,以此来判断该特征点是否是最优特征点,具体步骤如下:
在训练图片上利用FAST算法找到所有角点。为每个角点存储一个向量,这个向量一般有16位,代表这个点周围的16个像素。这个向量中的每一位都可以由式(1)所表示。在进行了上述处理以后,需要定义一个标志位变量来记录这个点是否是角点,如果是角点,就将标志位记为True,如果不是角点,就将标志位记为False。最后利用ID3算法递归地查询该特征点的每一个子集,递归终止的条件是所有子集的熵变成0
(1)
1.1.3 去除邻域位置多个重复冗余的特征点
先计算某个特征点周围像素灰度差值的绝对值来作该特征点的分数,如果该特征点邻域范围内还存在其它的特征点,也利用相同的方式,取其周围像素灰度的差值来作为分数,最后统计这些邻域特征点的分数,将其放在一起进行比较,选取分数最高的那个特征点作为该邻域范围内的唯一特征点,其它分数不是最高的特征点就不需要了,利用非极大值抑制的方式将其去除掉。非极大值抑制的公式如式(2)所示
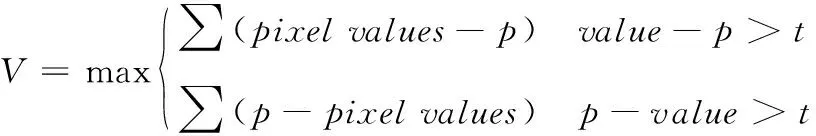
(2)
ORB算法采用的Oriented FAST关键点采用灰度质心法实现了旋转不变性,与FAST角点相比,不仅记录了位置信息,同时也记录了方向信息。若某个角点的坐标为O,则取该角点一定半径内的像素灰度进行计算,灰度质心法中的矩的定义如下
(3)
其中,I(x,y) 为图像灰度表达式。该矩的质心为
(4)
由式(4)的质心坐标可以计算得到特征点的方向,计算公式如下
(5)
1.2 BRIEF描述子生成算法
利用FAST角点检测算法后可以在图像上得到很多特征点,但这些特征点只有其自身信息,没有周围邻域的信息,在纹理单一、灰度相同的地方没法判断这些点在两幅图像上的对应位置,因此需要将该点的邻域信息也作为该点的一个属性,这个属性就是描述子,BRIEF算法就是一种描述子生成算法,该算法在FAST算法提取出来的特征点周围邻域选取多个点对,如果一个点对的灰度比较结果是大,则记录为1,否则记录为0,最后会生成一个类似的二进制编码串,通常情况下N选取128、256或者512。
ORB算法的特征描述是由BRIEF算法改进的,称之为rBRIEF(rotation-aware brief),rBRIEF算法在原有特征描述算法的基础上加入旋转因子,以此来保证提取描述子的过程中能够保证自身的旋转不变性,不会影响到描述子的生成质量。
描述子生成步骤:
(1)利用方差为2,窗口大小为9×9的窗口对图像进行高斯滤波,这样做的目的是为了减少噪声干扰。
(2)选取某一个特征点,在其邻域范围内随机选取一个点对x和y,选取的次数根据所需要的描述子长度而定,每选取一个对点后,就进行这两个点的灰度比较,如果x的灰度比y大,则记为1,否则记为0。具体计算公式如式(6)所示
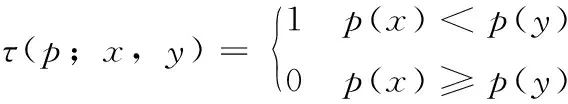
(6)
其中,p(x),p(y)分别是随机点x=(u1,v1),y=(u2,v2) 的像素值。
根据所需要的描述子长度进行多次比较之后,即可得到一个长度为所需要长度,每一位的值都是0或1的二进制编码串,这个串就表示该特征点的周围邻域信息,也就是它的描述子属性,BRIEF描述子所对应的十进制数如式(7)所示
(7)
ORB算法采用的描述子是Steer BRIEF描述子,与BRIEF描述子相比,利用了关键点的方向信息,进而实现了描述子的旋转不变性。具体方法是利用灰度质心法所得到的特征点的方向构建旋转矩阵,利用该旋转矩阵对随机生成的BRIEF描述子矩阵进行变换,最终得到具有方向不变性的Steer BRIEF描述子。
传统的ORB算法提取出的特征点过于集中,会出现扎堆的现象,不仅会降低一些需要对图像进行特征点提取的算法的效果,比如说SLAM,同时也会减少一幅图像上的信息量。通过对图片划分区域,从每个区域提取特征点可以保证最大程度上地使用图片上的信息,同时也增加了算法的鲁棒性。步骤如下:
(1)首先对图像金字塔上的每层都划分网格。
(2)利用FAST角点检测器对每层金字塔图像提取FAST角点,在纹理比较弱的区域如果没法提取出特征点,就适当降低提取的阈值,以此保证能够从整张图像上获取到足够的FAST角点。
判断是否是FAST角点的方法是比较某点像素与其周围像素灰度的差值是否满足某个阈值条件。利用角点响应函数和设置好的阈值T进行分析,倘若周围16个像素点与p点的灰度差值之和大于T,则像素p即被判定为角点。角点响应函数如下
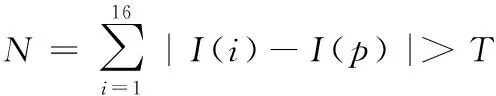
(8)
(3)利用四叉树的思想,对每个网格中提取的特征点进行筛选,筛选方法是如果该网格中不存在特征点,则删除该网格;如果该网格中存在特征点,则继续将该网格划分成四等分,再次判断每个网格中是否存在特征点,最后按照一定的策略,挑选出分布均匀的FAST角点。
1.3 四叉树策略筛选特征点
对于提取出的大量特征点,需要对这些特征点进行筛选,最终获得满足数量的特征点,但因为选择策略的不同,会导致最终提取的特征点在图像上的位置有所差别,影响最终特征点匹配的效果。因此本文采用四叉树的筛选策略挑选特征点。
具体策略如下:
(1)首先需要确定初始的图像中大概能分出几个原始节点。将利用原始ORB算法提取过大量特征点的图像分成几份,一般将分辨率为640×480的图像只分成一个节点,也就是四叉树的根节点。
(2)若原图像本来只有一个节点,则该节点在经历第1次分裂后,1个根节点分裂成为4个节点,每个节点中的特征点就是落在该节点范围内的特征点,都是来自原来的那个大节点。每次分裂完后需要统计每个节点中的特征点数量,如果某个节点所包含的特征点数量为0,那么就删除该节点,如果某个节点里特征点数量为1,则该节点不再进行分裂,但不进行删除,永远保留下去,直到分裂终止再进行处理。如果该节点中特征点数量大于1,则表示节点还可以再分裂,每次分裂完后判断此时的节点总数是否超过设定值,如果没有超过则下次分裂时对那些仍然可以分裂的节点进行分裂。
需要注意的是,一个父节点在经过一次分裂之后就变成了4个子节点,而对于原来的父节点将不再需要,直接将其删除,从总数量上来看,每次分裂都会增加3个节点,而不是增加4个节点。利用上述规律可以提前判断大约分裂多少次之后就可以达到所需要的节点总数阈值,计算方式为:当前节点总数+即将分裂的节点总数×3。
(3)若新分裂的节点里的特征点还是大于1个,就再次分裂成4个节点。如此往复,一直分裂,分裂终止条件是节点的数量大于所需要提取出的特征点数量,或者所有节点都无法再分裂。
当出现很多个节点中所包含的特征点数量都大于1,都能进行下一次分裂的情况,这时采用的策略是优先分裂特征点数量最多的节点,然后分裂特征点数量次高的节点,以此类推,通过把特征点数量多的节点先分裂开来的策略可以使得特征密集的区域能够更加细分。如果某些节点所包含的特征点比较少,可能会因为提前达到了节点阈值要求而不需要再分裂了,保证了提取时充分考虑到所有节点,提高了提取的准确性。
(4)当分裂达到节点阈值这个终止条件时,从所分裂出的每一个节点中利用非极大值抑制的思想选择出角点响应值最高的特征点作为这个节点的代表特征点,而其它响应值低于该节点的特征点都将被删除,不需要进行保留,通过四叉树的策略从提取出的大量特征点筛选出合适的特征点,就得到了分布比较均匀且数目达到要求的特征点。
四叉树策略筛选特征点如图2所示。
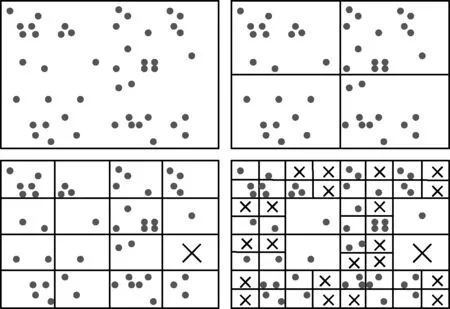
图2 四叉树筛选特征点流程
2 GMS算法剔除误匹配
对于暴力匹配后的结果,存在大量的误匹配,利用GMS算法可以剔除误匹配。该方法通过统计正确和错误匹配邻域的可区分度,来判断该匹配是否正确,进而剔除误匹配。GMS匹配方法基于假设:如果匹配是正确的匹配,那么这个正确匹配的小范围内的匹配集中在三维空间的同一个区域。同样地,一个错误匹配的小范围内的匹配会出现在三维空间的不同位置,几乎不会出现在同一个区域。
假设输入图像I1有N个特征匹配,输入图像I2有M个特征匹配;定义C={c1,c2,…,ci,…,cN} 来表示图Ia到图Ib的最近邻匹配,其中ci表示像素点pi与qi的匹配;定义ci的领域为
Ni={cj|cj∈C,cj≠ci,d(pi,pj)}
(9)
根据式(9)可以得到ci的相似领域,如式(10)所示
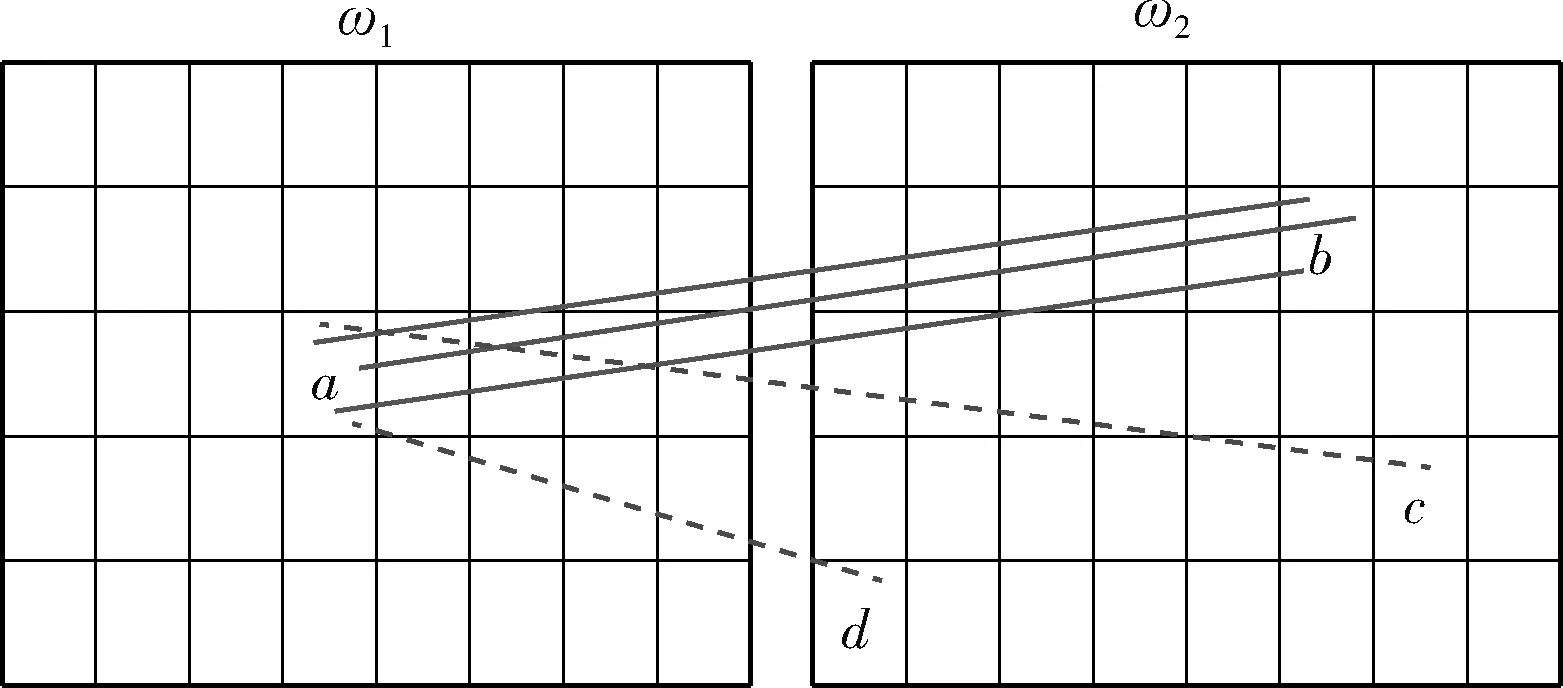
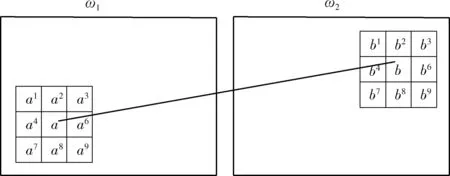
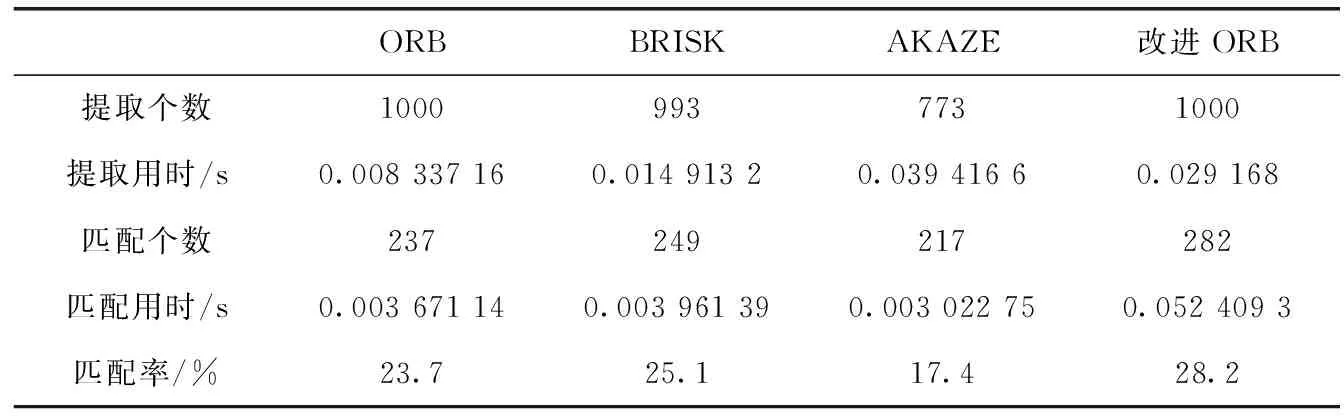
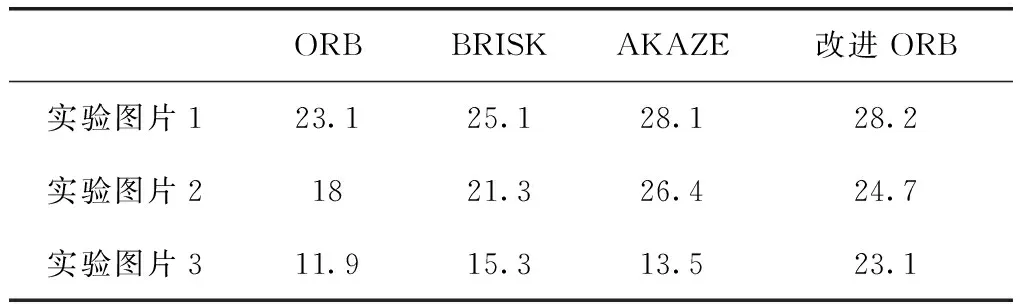
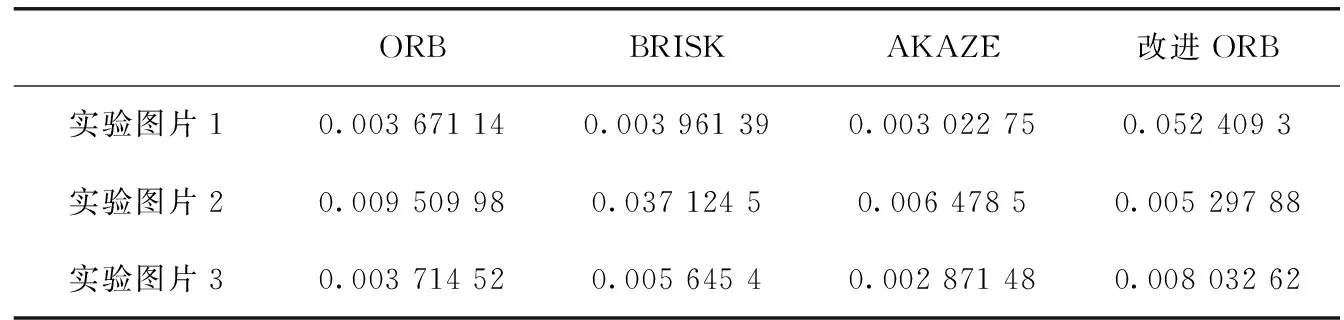
Si={cj|cj∈Ni,d(qi,qj) (10) 其中,Si中元素的个数,也就是匹配ci的运动支持,用 |Si| 表示,d(·,·) 是两点之间的欧式距离,r1和r2为距离阈值。对 |Si| 建模,如式(11)所示 (11) 其中,错误匹配被其某个邻域窗口匹配支持的概率用ε表示,正确匹配被其某个邻域窗口匹配支持的概率用t表示,邻域Ni内匹配对的数量用 |Ni| 表示。通过分析得到式(11)期望为 (12) 以及式(11)的方差为 (13) 正确和错误匹配的可区分度可以通过期望和方差来表示,如式(14)所示 (14) 利用基于划分网格的算法可以对以上算法进行加速,将两幅需要进行匹配的图像按照某种策略划分成很多个小网格:ω1以及ω2,ci表示落在网格Ga和Gb中的一个匹配对,在图3中用一条实线段表示。于是邻域(表示在网格Ga中的匹配)被重新定义为 Ni={cj|cj∈Ca,ci≠cj} (15) 相似邻域被重新定义为 Si={cj|cj∈Cab,ci≠cj} (16) 图3 基于网格的框架 式(15)和式(16)中,Ga表示某个网络,Ca表示落在Ga中的匹配对,Cab表示同时落在Ga和Gb中的匹配对。算法定义邻域为落在同一网格中的匹配,定义相似邻域为同时落在两个网格中的匹配,即区对。 算法的性能与网格的大小有关系,如果网格非常小,那么很多邻域信息都将忽略,但与之相反,并不是网格越大越好,网格的大小过大会将很多不正确的对应关系也包含进来。因此网格大小的选取即为重要,既不能忽略太多的邻域信息,也不能将太多的错误信息包含进去,为了解决邻域信息包含太少的问题,采用运动内核来将更多的邻域信息包含进去,同时为了提高算法的准确性,也需要将网格设置的比较小,如图4所示。 图4 运动核 根据网格设置较小,采用运动内核的思路,在原有网格邻域的8个网格的基础上构成了一个更大的网格 (Ca1b1,…,Ca9b9)。 由此重新定义了邻域 Ni={cj|cj∈CA,ci≠cj} (17) 重新定义相邻邻域 Si={cj|cj∈CAB,ci≠cj} (18) 其中,CAB=Ca1b1∪Ca2b2∪Ca3b3…∪Ca9b9。 针对旋转问题,利用旋转运动核模拟不同方向的旋转,如图5所示,固定CA, 对CB按照顺时针旋转,这样可以得到8个运动核,然后在所有运动核上使用GMS算法,然后选择最好的结果(选择匹配数量最多的那个)。 图5 旋转运动核 本文融合GMS的改进ORB算法的总体流程如图6所示。 图6 改进ORB算法总流程 本次实验所使用的CPU为Intel i5-9300H,频率为2.40 HZ,显卡为GTX1650,所使用的操作系统为Ubuntu16.04,进行测试的图片选自TUM数据集,选取的3张图片其桌面物体的纹理比较丰富,但桌面和地板纹理单一,很适合本次实验。实验图片如图7所示。 图7 实验测试图片 特征点提取算法种类很多,例如ORB算法、BRISK算法以及AZAKE算法等,但这些算法都没法在纹理比较弱的地方提取出足够的特征点,甚至可能一个特征点都提取不出来。上述算法提取出的特征点大多数都集中在纹理比较丰富的地方,使得图片很大部分区域的信息都没有利用上。因此针对上面的问题,将四叉树策略应用到特征点提取中,对大量粗提取的特征点进行精提取,充分利用图片上的信息,最终提取出分布比较均匀的特征点。 利用改进的特征点提取匹配方法对实验图片1进行特征点提取,分别对比了ORB算法、BRISK算法和AZAKE算法与改进后的ORB特征点提取匹配方法的效果。 如图8的实验结果所示,ORB算法、BRISK算法和AKAZE算法提取的特征点分布比较密集,基本集中在纹理比较丰富的桌子上的物体,但对于纹理比较弱的地板和桌面,基本提取不出特征点,很不利于对整张图片信息的利用。而对于改进的ORB算法提取的特征点分布比较均匀,可以从图8(d)中看出,地面以及桌面等纹理比较弱的地方,也可以提取出比较多的特征点,最大程度地保留了图片上的有用信息。 图8 4组实验结果 传统的暴力匹配的方式在匹配完后存在一些误匹配的情况,匹配的准确性将影响到很多算法的准确性,因此在暴力匹配结束后,利用GMS算法基于网格模型对匹配后的特征点进行误匹配剔除,最终可以获得非常准确的匹配结果。 利用3组图片分别对原始ORB算法、BRISK算法、AKAZE算法以及改进的ORB算法进行特征点匹配实验。 如表1所示,对实验图片1进行特征点提取与匹配,改进的ORB算法,如图9所示,匹配率达到28.2%,比ORB算法高了4.5%,其效果与AKAZE算法效果相当,但特征点提取用时上却比ORB算法用时高了3倍时间,匹配用时也比其它算法用时高一些,但总体上并不影响该算法的实时性。 表1 4种算法特征点提取匹配效果对比(采用实验图片1) 图9 改进ORB算法匹配效果 表2中显示的是原始ORB算法、BRISK算法、AKA 表2 4种算法在不同图片上的匹配率/% ZE算法以及改进ORB算法在不同图片上的匹配率。对于实验图片1,改进后的ORB算法匹配率为28.2%;对于实验图片2,算法的匹配率为24.7%;对于实验图片3,算法的匹配率达到23.1%;可以看出,改进的ORB算法匹配率与其它算法相比,显得更加优秀,可以获得更高的匹配率。 表3显示的是原始ORB算法、BRISK算法、AKAZE算法以及改进的ORB算法在不同图片上的匹配用时。从中可以看出,由于引入GMS算法,整体的匹配用时变长了一些,但在某些图片上与其它算法的用时相差不大,甚至比一些算法的匹配用时短,对于基本的实时性,改进后的ORB算法可以满足。 表3 4种算法在不同图片上的匹配用时/s 针对传统的ORB特征点提取算法提取的特征点位置分布不均匀的问题以及存在误匹配的问题,提出了一种改进的ORB算法,对图像分区域提取特征点并与GMS匹配算法相结合,首先对图像整体提取特征点,然后利用四叉树原理对提取出的特征点分区域进行挑选,最终得到分布相对均匀的特征点,其次通过GMS算法将特征点的运动平滑约束转变为剔除误匹配的统计量,对提取出的特征点进行匹配和误匹配剔除。 实验结果表明,改进后的ORB算法在测试图片1上的匹配率达到了28.2%,比原始ORB算法提高了4.5%,达到了更高的匹配率,且所匹配出来的特征点与其它算法相比更加均匀,能够有效地利用到整个图片的信息。同时该算法用时虽然有些许增加,但并不影响其实时性。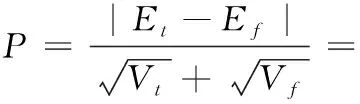
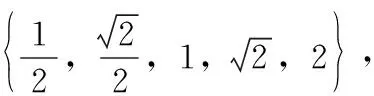
3 实验验证分析
3.1 实验平台

3.2 改进ORB算法图像提取实验

3.3 改进ORB算法图像匹配实验

4 结束语

