有限长圆柱壳-流场部分耦合系统声振建模及机理研究

郭文杰, 杨 舟

(华东交通大学 交通运输工程学院， 南昌 330013)

圆柱壳-流场耦合系统在船舶与海洋工程、油气储运工程、航空航天工程等诸多领域有广泛的应用，如潜艇、输油管路、含液体燃料的火箭贮箱等。早期的研究主要针对圆柱壳内部充满液体[1-3]或者浸没于无限域[4-6]这类理想工况，由于结构表面与流场完全耦合且不考虑自由液面声边界的影响，数学处理难度较低，可直接将声压在结构位移场坐标系展开，再根据流固耦合面速度连续条件得到声场与位移场的数学联系，已形成了一套非常清晰的研究思路。

实际的工程问题中，圆柱壳与流场两种介质也常处于部分耦合的状态(圆柱壳轴线与自由液面平行)，比如海面系泊状态(浮态)下的潜艇、油气混输管道、未盛满液体的圆柱型储液容器等，其动力学特性关系到结构的安全性、功能性，因此开展相关理论研究工作尤为必要。

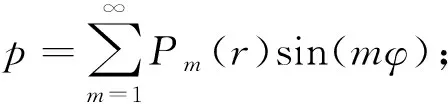
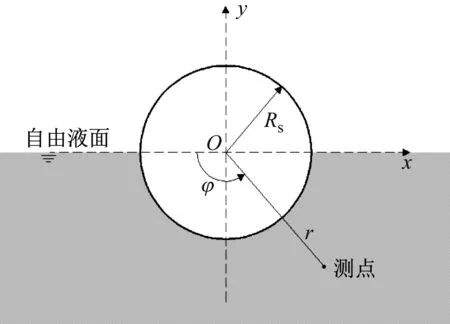
(a)

(b)

(a)

(b)

为了克服上述不足，首先就是需要突破惯性思维的桎梏。针对部分耦合问题的建模难点，郭文杰等[19-20]在实践中探索出利用声场、结构两套不同坐标系建模的方法，并成功对无限长圆柱壳-外流场部分耦合声振问题进行建模求解。具体来讲，结构位移场建立在以壳体圆心为坐标原点的柱坐标系下，便于描述壳体运动，声场坐标系的原点建立在自由液面上，便于利用正弦函数得到声压函数表达式，接着利用Galerkin法处理声固耦合面上振速连续条件，得到声场和位移场系数向量的矩阵关系，进而可对耦合系统振动特性进行理论求解。基于两套坐标系建模方法，Zhao等[21]研究了简谐点荷载作用下无限长部分浸没圆柱壳的声辐射特性，并开展试验验证。

在前期基础上，本文进一步将圆柱壳模型由无限长拓展到有限长，即考虑轴向波数对声固耦合系统的影响。此外，为深入探究内、外声场与圆柱壳结构耦合振动问题的异同，本文对相同液面高度下部分充液与部分浸没工况开展辨析研究，并从数学机理上揭示其异同的成因。

1 理论推导

1.1 模型描述

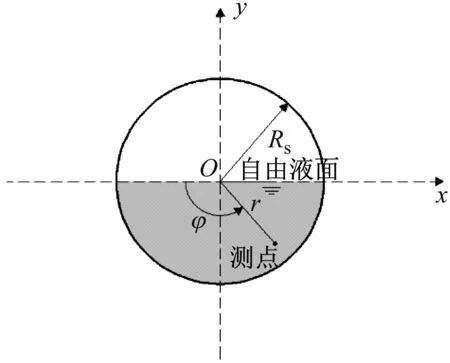
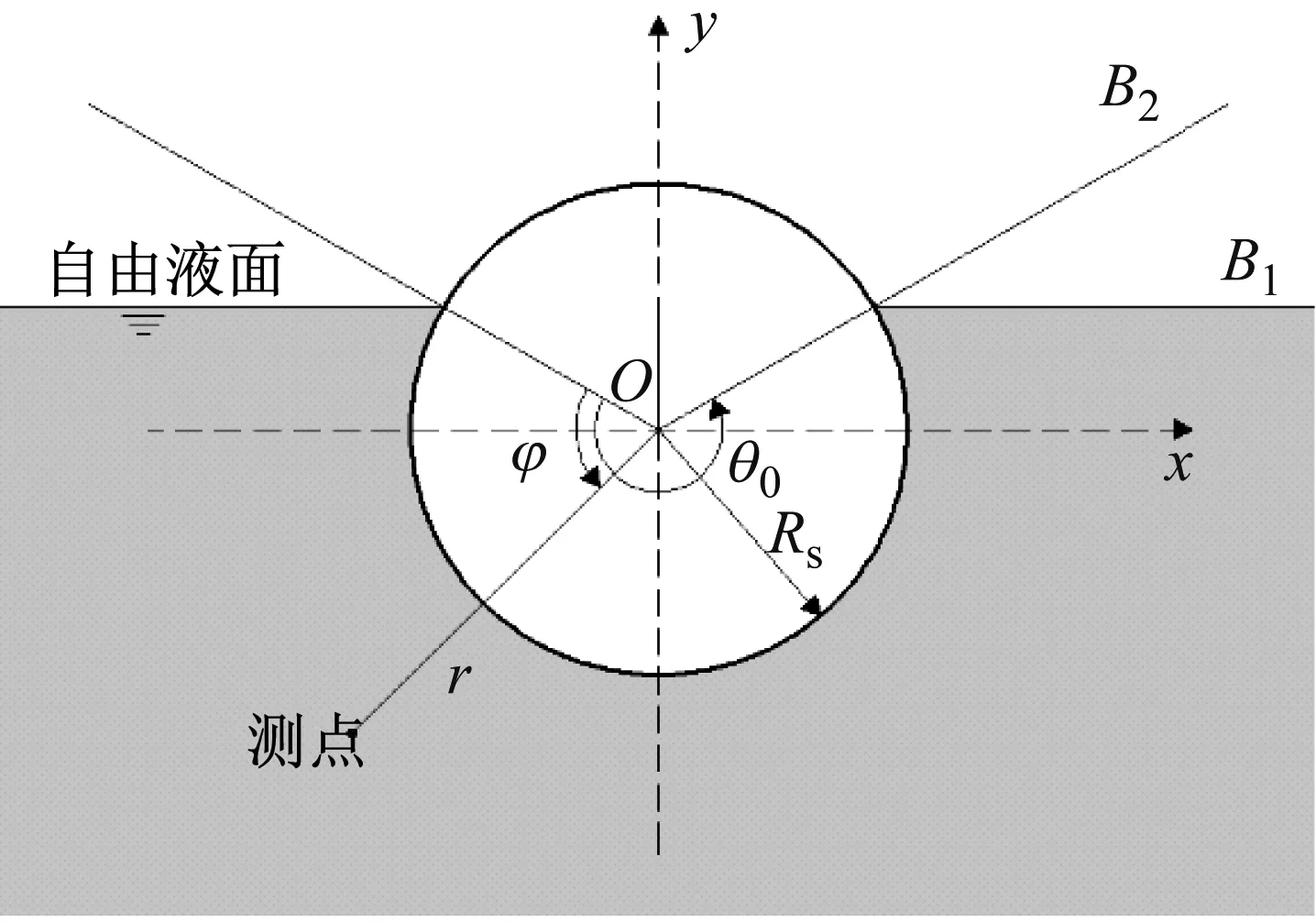
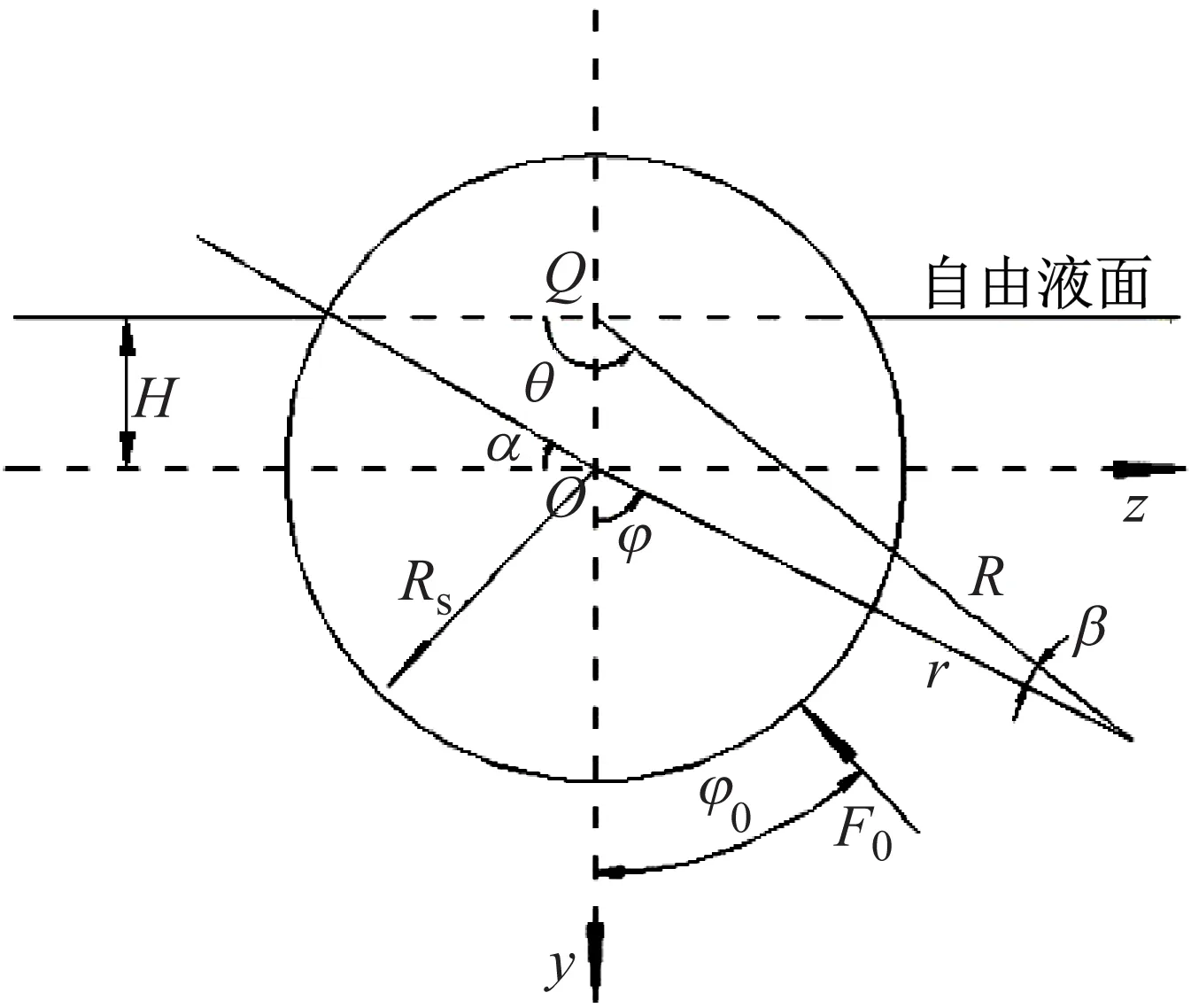
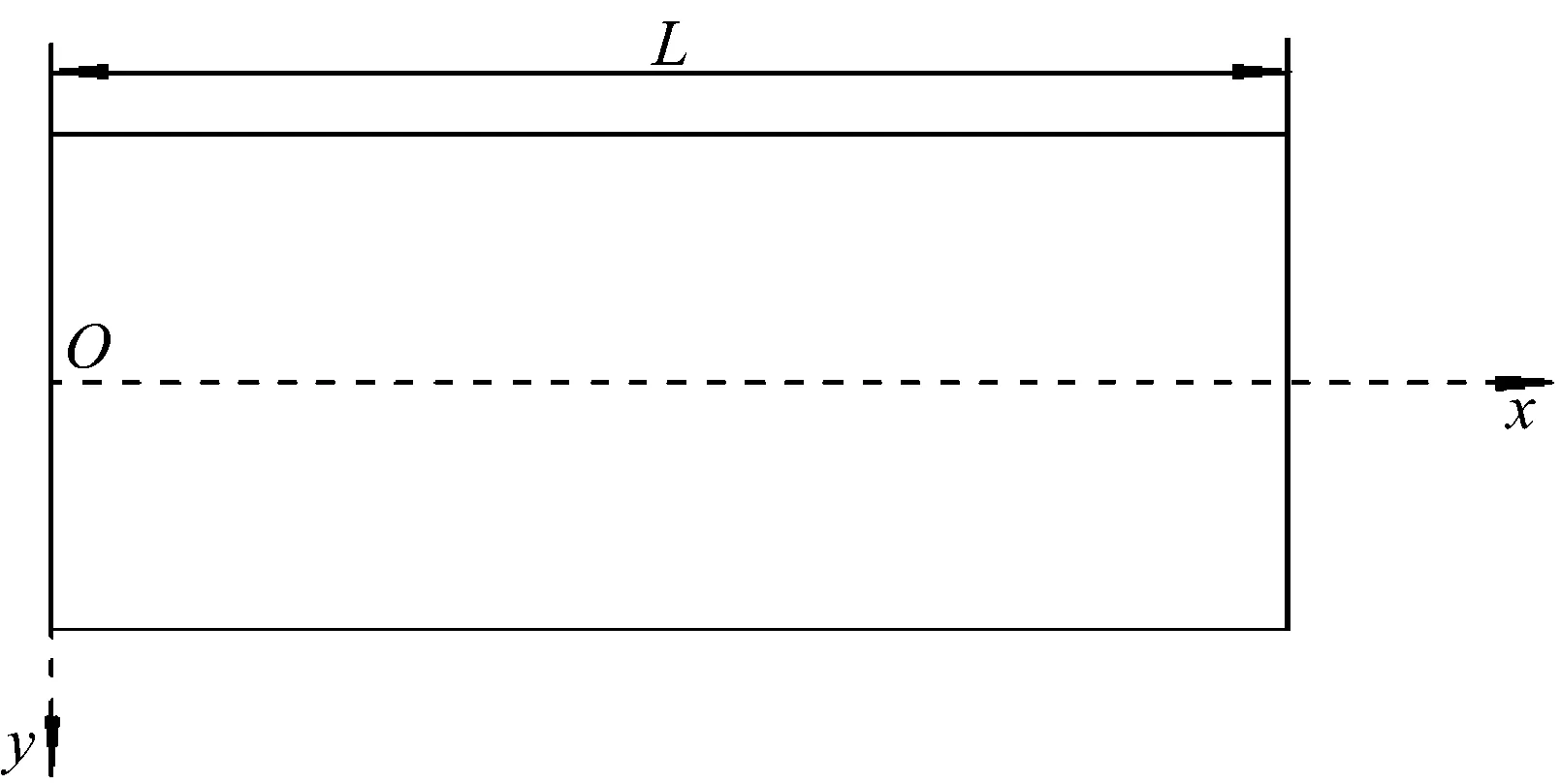
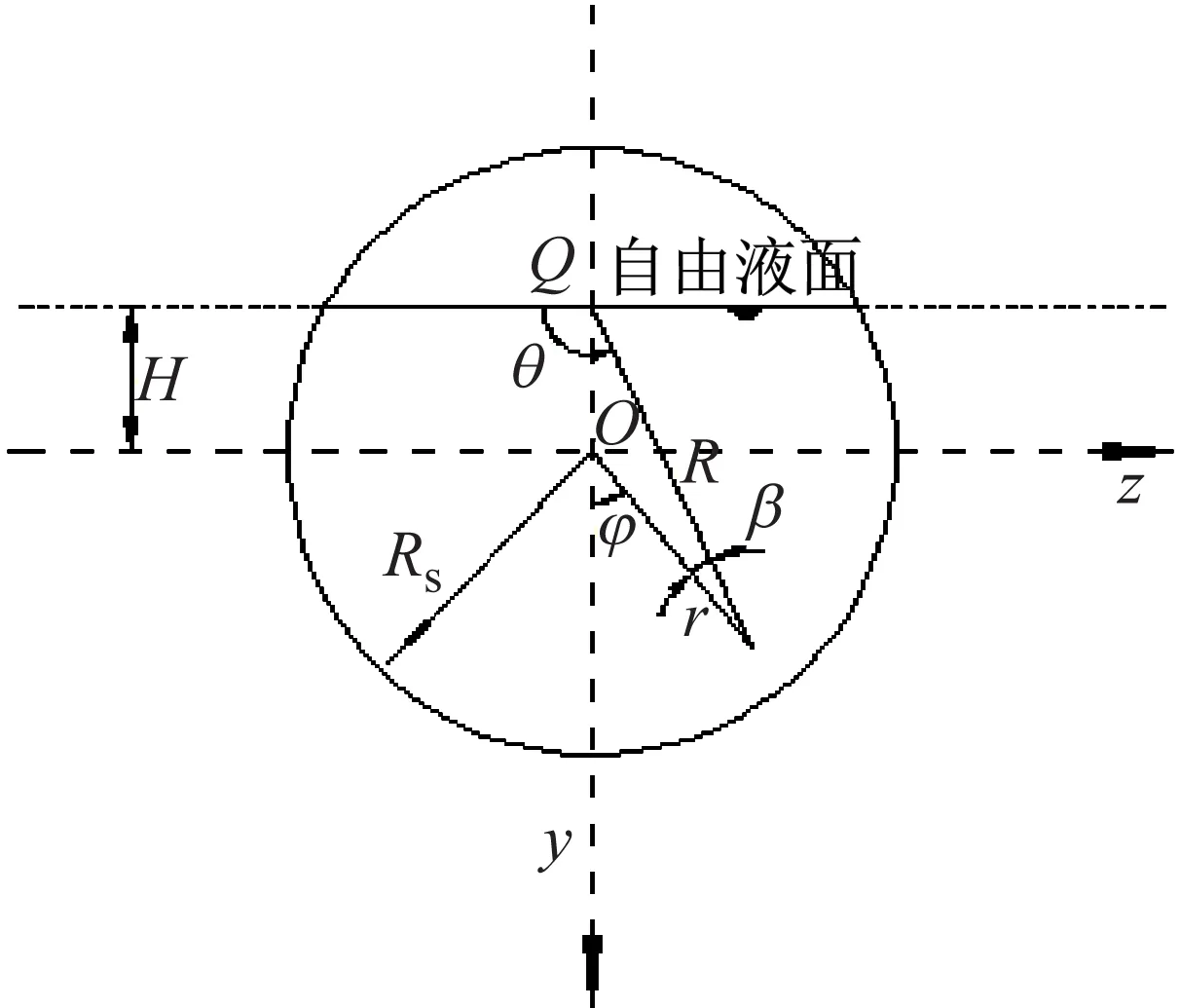
有限长圆柱壳参数定义如下：壳长为L，壳厚为h，横截面中面半径为Rs，结构密度为ρ，杨氏模量为E，泊松比为μ，流体密度为ρf。壳体坐标系原点O位于左端面圆心，相应的直角坐标(x,y,z)如图3所示。实际理论推导中壳体坐标系采用柱坐标系(x,r,φ)，其中：x，r，φ分别表征轴向、径向、周向角(起始点为y轴正方向，逆时针为正)。声场坐标系原点定义为y轴与自由液面交点Q，同样采用柱坐标系(x,R,θ)，R表征径向，θ表征周向角，逆时针为正。定义Q点于y轴坐标值的负数为液面特征高度H(位于y轴负半轴取正值)。α为液面对应的夹角，满足H/Rs=sinα。结构坐标系与声学坐标系夹角定义为β，当自由液面在壳体圆心上方时β取值为正值。简谐激励力位于结构坐标系(Rs,x0,φ0)处，幅值为F0。

(a)

(b)

1.2 结构运动方程

圆柱壳运动方程建立在结构坐标系(x,r,φ)下，采用Flügge壳体理论描述

(1)

式中：u，v和w分别为轴向、周向和径向的位移；fr为外力载荷；fp为圆柱壳内表面的流体负载，[L]为经典的Flügge壳体理论微分算子，详见文献[22]。

为了研究的方便，本文假设结构两端的边界条件均为简支，由此位移场及载荷可展开为三角级数形式(时间项略去)

(2)

式中：Umn，Vmn和Wmn分别为3个方向位移的幅值；fmn为流体负载fp的幅值；Fmn为外力载荷fr的幅值；m为轴向半波数；n为周向函数展开序列数；ω=2πf为角频率，f为频率；轴向波数km=mπ/L。

基于函数的正交性，可将式(2)代入式(1)，并进行正交化处理，即可得到如下的控制方程

(3)

式中，矩阵[T]中的具体算子详见Guo等的研究。

根据式(3)可进一步化简，消去Umn，Vmn后可得到形式更为简洁的振动控制方程

(4)

式中，Imn=(T11T22-T12T21)/det(T)。

点激励力可以表示为如下的函数形式，国际单位为N

(5)

式中，δ(·)为狄利克雷函数。

同样对式(5)进行正交化处理，可以得到激励力幅值Fmn的表达式

(6)

1.3 声场建模

声场建模是理论研究的一大重点，而声边界的处理是声场建模的主要难点。要对部分耦合系统进行理论研究，就必须建立满足所有声边界条件的数学模型。首先，声压p必须满足声学Helmholtz方程

(7)

式中：kf=ω/cf为声波波数，ω=2πf为角频率，f为频率；∇2为拉普拉斯算子。

然后，声压p还要进一步满足无穷远处Sommerfeld辐射条件

(8)

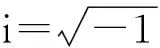
最后，声压p还需于自由液面处满足声压释放条件(空气密度相比水的密度极小，且声速也相对较小，故而空气的特性阻抗远小于水，因此水中声波入射到液面时可作为绝对软边界处理，即认为声压为零

p=0, 自由液面处

(9)

本文将声压函数建立在独立的声场坐标系(x,R,θ)下，然后通过采用正弦三角级数来自动满足液面处声压释放条件，具体形式如下

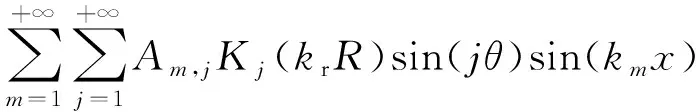
(10)

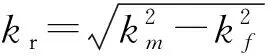
由于声压负载在结构表面部分存在，可以写成分段函数的形式

(11)

根据式(2)中载荷的展开形式，基于正交化处理可以得到声压负载fp幅值fmn的表达式

(12)

1.4 控制方程求解

根据控制方程式(4)可知，在确定声压负载幅值fmn的表达式后，控制方程求解的关键在于构建声压幅值和位移幅值的数学联系。

根据声固耦合面处位移连续条件，声压与径向位移有如下关系

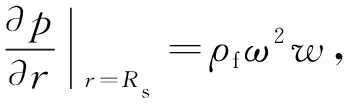
(13)

由于式(13)难以直接解析求解，可选择合适的数值方法进行求解。由于Galerkin法具有计算精度较高、适用性较广的优点，本文选择该方法对式(13)进行数值求解。构成位移场和声场的基函数主要有两类，对应的权函数也有两类，一类基于位移周向展开函数；另一类基于声压周向展开函数

(14)

因此可将方程式(13)转化为二重积分的弱形式，且积分域为声固耦合面

(15)

式中：n取值为-N～N；j取值为1～2N+1，N为截断项数。

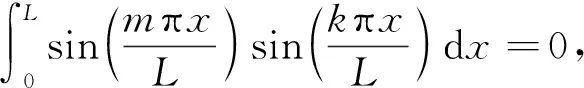
ρfω2[Vs]{Wmn}=[Vp]{Amj}

(16)

式中：[Vs]和[Vp]均为2N+1阶方阵，{Wmn}=[Wm,-N,Wm,-N+1, …,Wm,N-1,Wm,N]T为位移幅值向量；{Amj}=[Am,1,Am,2, …,Am,2N,Am,2N+1]T为声压幅值向量；上标T为对矩阵进行转置。

由于声固耦合面上(r,φ)坐标系和(R,θ)坐标系之间存在几何对应关系，根据式(15)，[Vs]，[Vp]中的元素可表示为如下积分形式(假设权函数基于径向位移的周向展开函数)

(17)

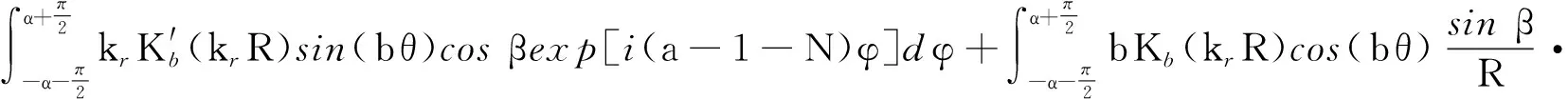
exp[i(a-1-N)φ]dφ

(18)

式中，β=3π/2-θ-φ,R和θ的取值满足如下几何关系

(19)

同时，式(12)中{fmn}也可表示为矩阵的形式

{fmn}=[Tp]{Amj}

(20)

式中，矩阵[Tp] 中每一个元素的具体表达式如下

N)φ]Kb(krR)sin(bθ)dφ

(21)

最终可以得到仅与径向位移幅值相关的耦合系统控制方程

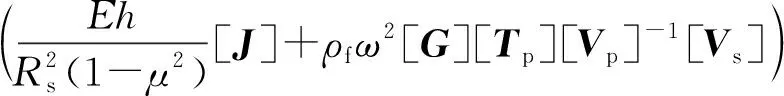
(22)

式中：矩阵[J]为2N+1阶单位矩阵；[G]矩阵为对角矩阵；[G]j, j=Im, j-1-N；{Fmn}=[Fm,-N,Fm,-N+1, …,Fm,N-1,Fm,N]T为激励力向量，详见式(6)。直接求解控制方程式(22)可得到位移幅值向量{Wmn}，进而可得到结构任意点振动位移响应。

当求解自由振动时，激励力为零，式(22)转化为特征值求解问题

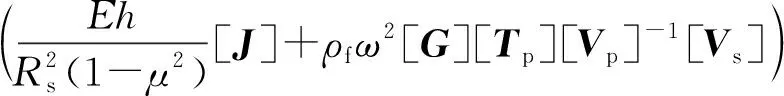
{0}

(23)

式中，{0}为零向量，具体求解时可通过定义式(23)中系数矩阵行列式值为零来求解角频率ω，再根据f=ω/(2π)，可以得到各阶固有频率。

2 数值分析

本文参数选择如下：结构密度ρ=7 850 kg/m3，弹性模量E=206 GPa，泊松比μ=0.3，壳体长度L=1.284 m，中面半径R=0.18 m，壳厚h=0.003 m，流体密度ρf=1 025 kg/m3，流体声速cf=1 500 m/s。当计算受迫振动响应时结构阻尼因子η取为0.01，复杨氏模量为E′=E(1+iη)。

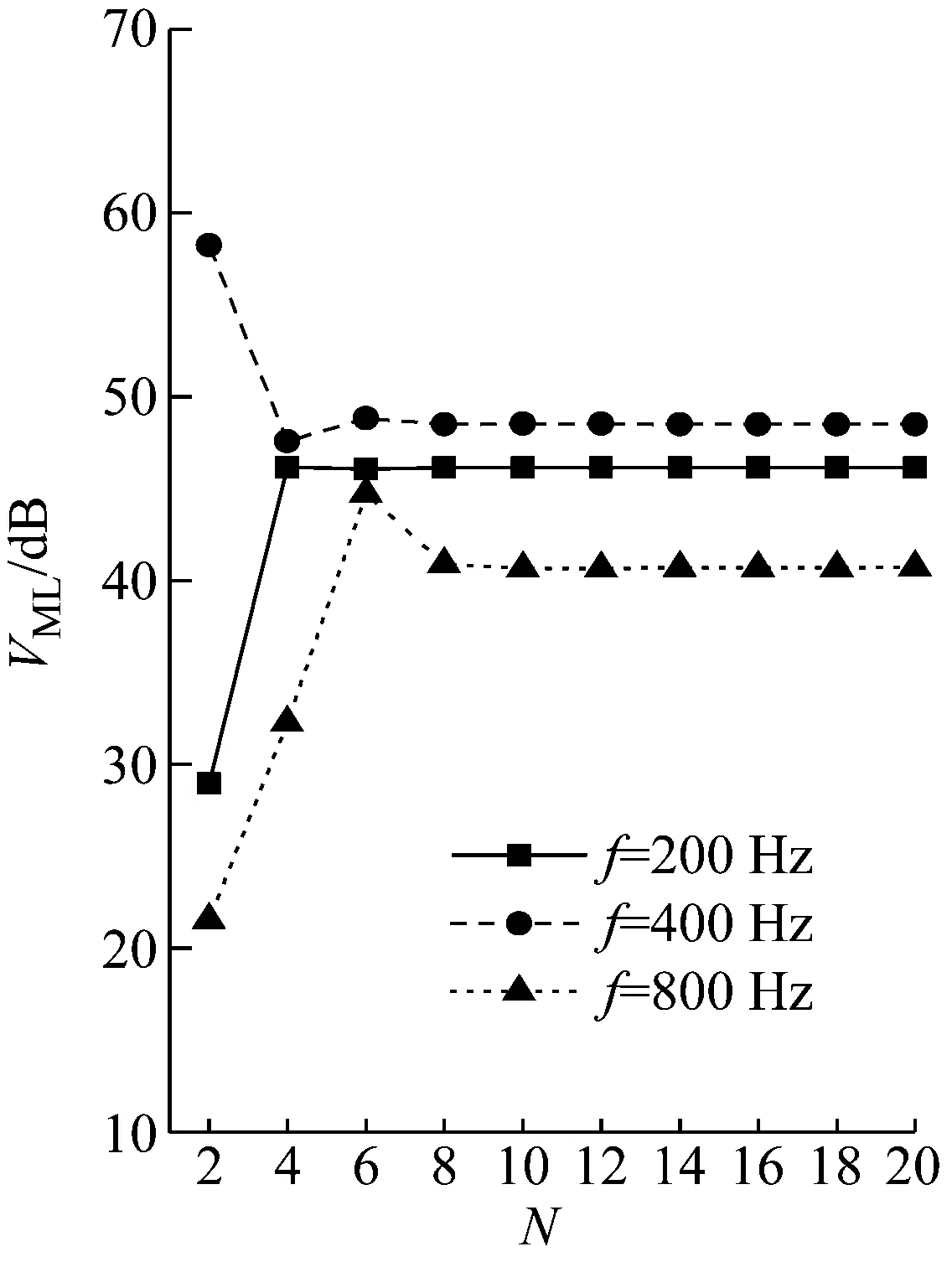
2.1 方法收敛性分析

由图4可以看出，随着截断项数M，N的增加，径向均方振速级VML很快趋于稳定；当激励频率在1 200 Hz以内时，M和N均取12时结果已足够收敛。后文计算中M，N取值均为12。

(a)

2.2 方法适用范围

接着进一步分析本文方法特征高度的取值范围，定义无量纲特征高度为H/Rs，取值为-0.8～0.8，间隔0.1。分别计算两种不同权函数下首阶固有频率值，并与有限元软件Nastran中仿真(虚拟质量法)计算结果进行对比，如表1所示。

由表1可知，权函数无论是位移基函数还是声压基函数，在保证计算精度较高的情况下，无量纲特征高度H/Rs取值范围为-0.8～0.8。由Amabili的研究可知，Amabili提出的斜边近似法适用范围约为-0.37～0.37，换句话说，本文方法适用范围相比斜边近似法要大得多。

2.3 方法准确性验证

接下来，本文开展了自由振动和受迫振动的方法准确性验证，且权函数选择位移基函数，有限元仿真对比继续采用虚拟质量法。

2.3.1 自由振动准确性分析

首先针对自由振动，本文分别取浸没深度H=-0.09 m，H=0和H=0.09 m，计算前10阶固有频率，并与有限元软件Nastran仿真计算结果进行对比，如表2所示。定义固有频率的相对误差Error=(f1-f2)f2×100%。

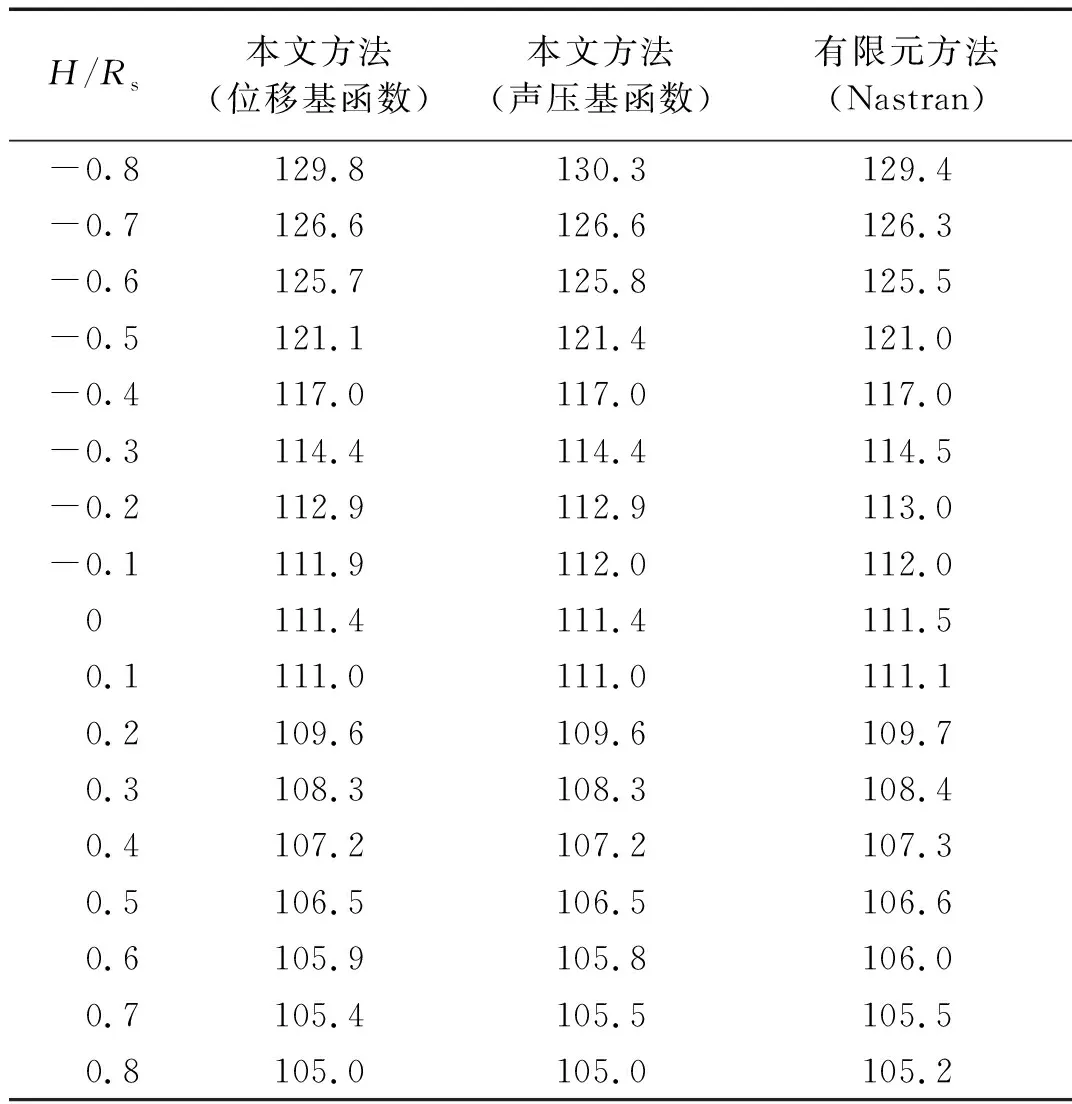
表1 各无量纲特征高度下首阶固有频率对比

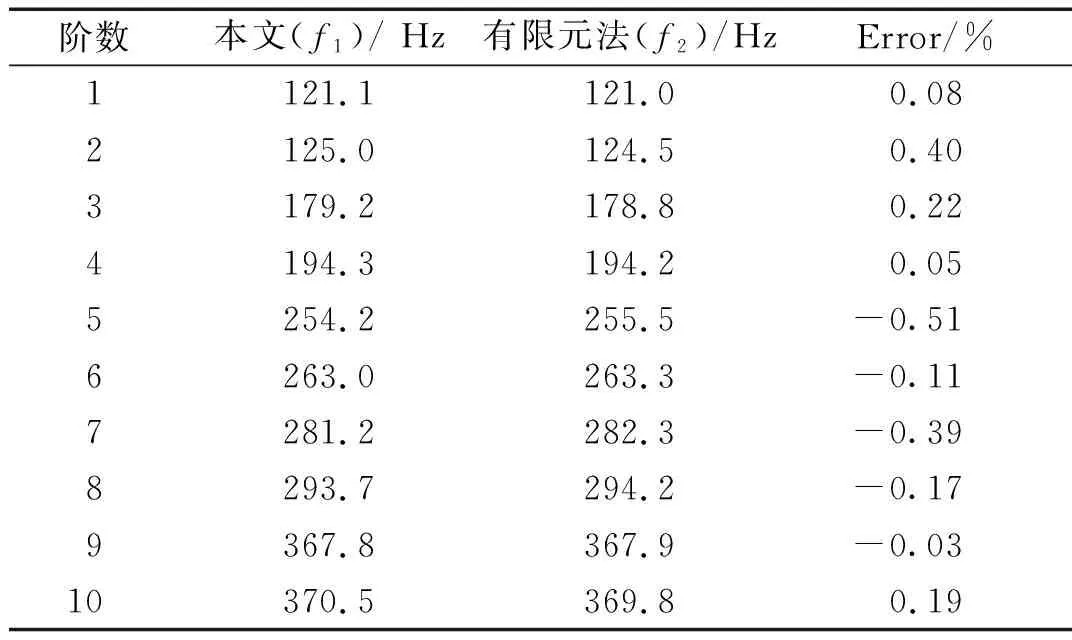
表2 当H=-0.09 m时部分浸没圆柱壳前10阶固有频率对比

由表2～表4可知，对于部分浸没圆柱壳，本文方法计算得到的前10阶固有频率与Nastran仿真计算结果十分吻合，最大相对误差的绝对值不超过1%，这也说明本文方法计算自由振动是准确可靠的。

2.3.2 受迫振动准确性分析

紧接着，本文进一步分析受迫振动时方法准确性。假设点激励力位于坐标x0=L/2，φ0=0处，激励力幅值F0=1 N，激励频率取值范围为2～500 Hz，间隔2 Hz。观测点位于坐标x1=L/4，φ1=0处。分别计算特征深度H=-0.09 m和H=0.09 m时径向位移响应级频谱曲线，并与有限元软件Nastran仿真(虚拟质量法)结果进行对比，如图5所示。本文定义径向位移响应级[23]RDL=20×lg(w/w0)，其中w为测点径向位移绝对值，w0=1×10-12m。

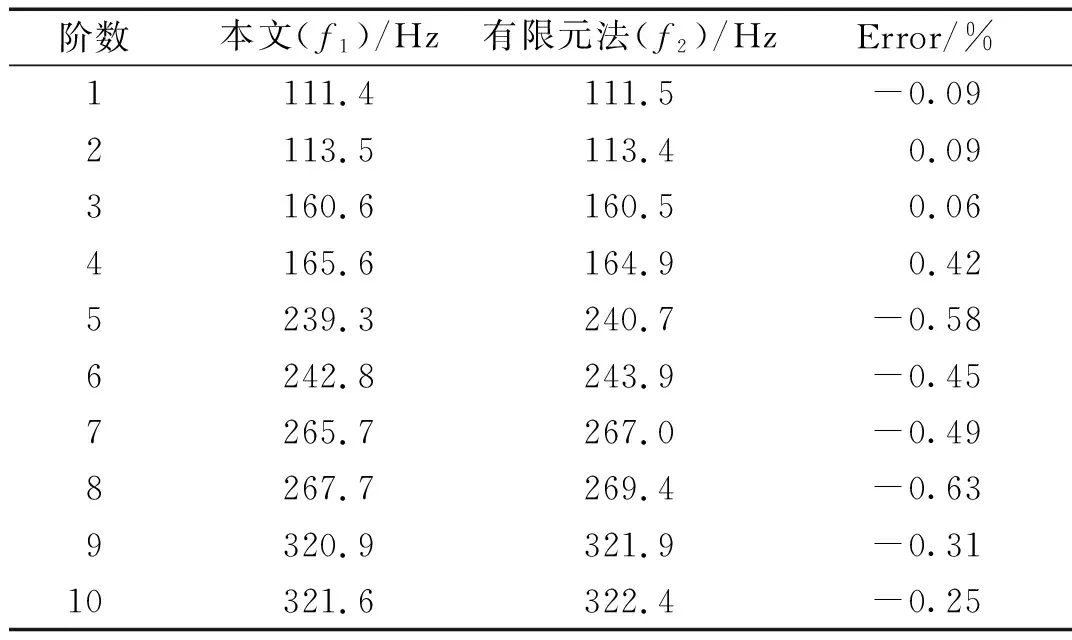
表3 当H=0时部分浸没圆柱壳前10阶固有频率对比

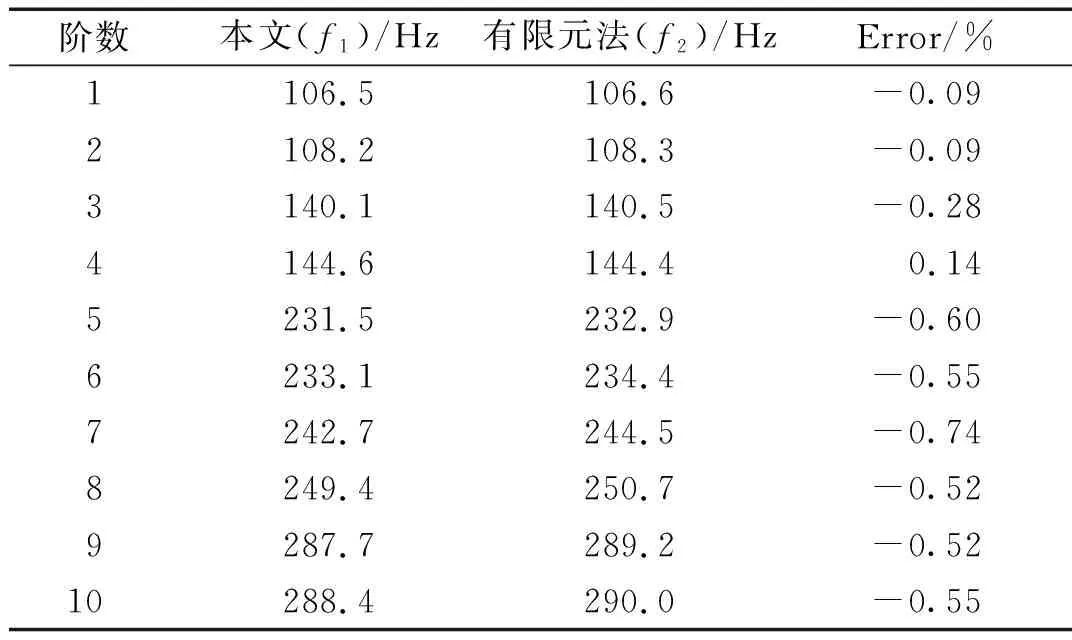
表4 当H=0.09 m时部分浸没圆柱壳前10阶固有频率对比

从图5可以看出，本文方法频响曲线和Nastran仿真结果吻合良好，进一步验证了本文方法的准确性。此外，本文方法计算效率远高于仿真方法(虚拟质量法)计算效率。以图5(b)中频响曲线计算为例，当计算机配置均为4 GHz CPU与24.0 GB RAM时，虚拟质量法在2 400个单元的仿真计算规模下耗时约2.2 h。而基于本文方法采用MATLAB2014a编程计算约耗时4 min，计算效率提高数十倍。

2.4 液面特征高度H对固有频率的影响

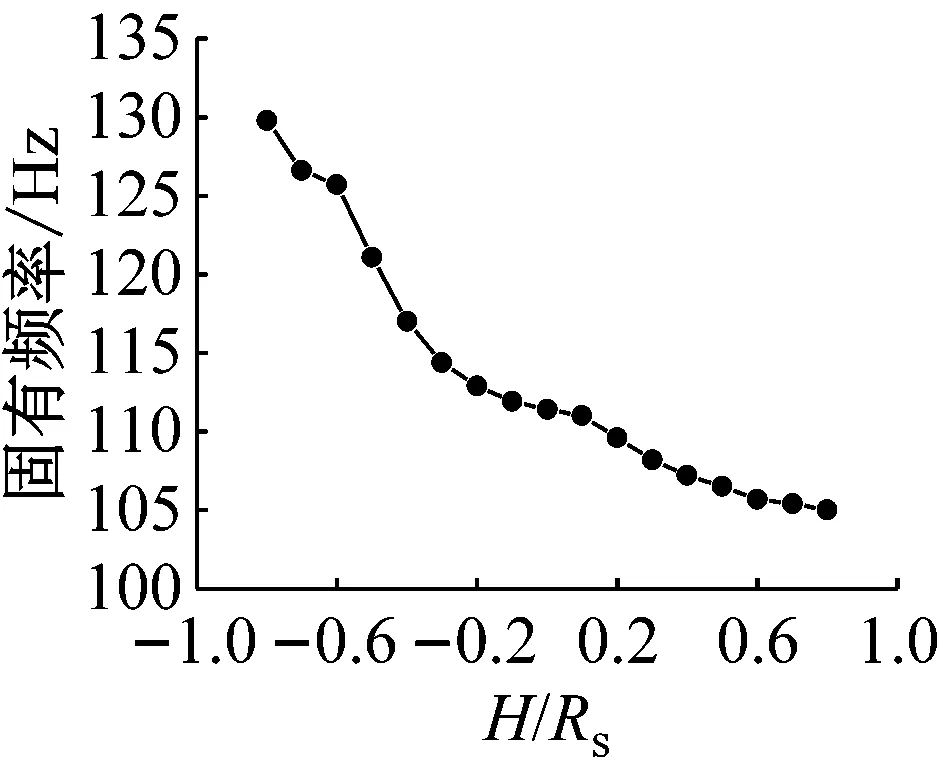
液面特征高度的变化会引起附连水质量的变化，进而影响耦合系统自振特性。为研究自振特性随特征高度的变化规律，取无量纲特征高度H/Rs为-0.8～0.8，计算前4阶固有频率随特征高度变化规律，如图6所示。

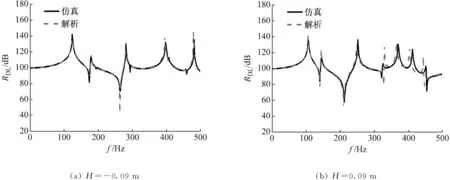
图5 不同方法下部分浸没圆柱壳径向位移级对比

(a) 第一阶

从图6可以发现，同阶次固有频率随着特征高度增大而减小，主要原因是由于特征高度增大导致湿表面积增加，因而使得附连水质量增加，从而增加了耦合系统的等效质量，导致同阶次固有频率降低。此外，同阶次固有频率随特征高度增加而下降的速率无显著规律，这是因为自由液面对声波的反射也会对附连水质量产生影响。因此在两类因素的综合影响下，虽然同阶次固有频率整体上随液面增高而降低，但是下降速率无明显规律，忽快忽慢。

3 部分充液工况

3.1 部分充液工况建模及求解特点

部分充液工况与部分浸没工况在理论建模及数学推导方面是基本相似的，如图7所示。但由于流场由外变内，主要存在两点差异：一是声学Helmholtz方程的基本解有区别；二是声固耦合面振速连续条件有方向差异。

3.2 部分充液工况下本文方法的准确性验证

为验证部分充液工况下本文方法的准确性，本节继续采用有限元软件Nastran的仿真计算结果作为对比。特征高度分别取H=-0.127 3 m，0，0.127 3 m，两种方法的前10阶固有频率对比如表5～表7所示。

从表5～表7可以看出，部分充液工况下本文方法计算得到的前10阶固有频率与Nastran仿真计算结果十分吻合，最大相对误差的绝对值不超过1%，这也说明本文方法计算部分充液圆柱壳振动特性是准确可靠的。

(a)

(b)

表5 当H=-0.127 3 m时部分充液圆柱壳前10阶固有频率对比

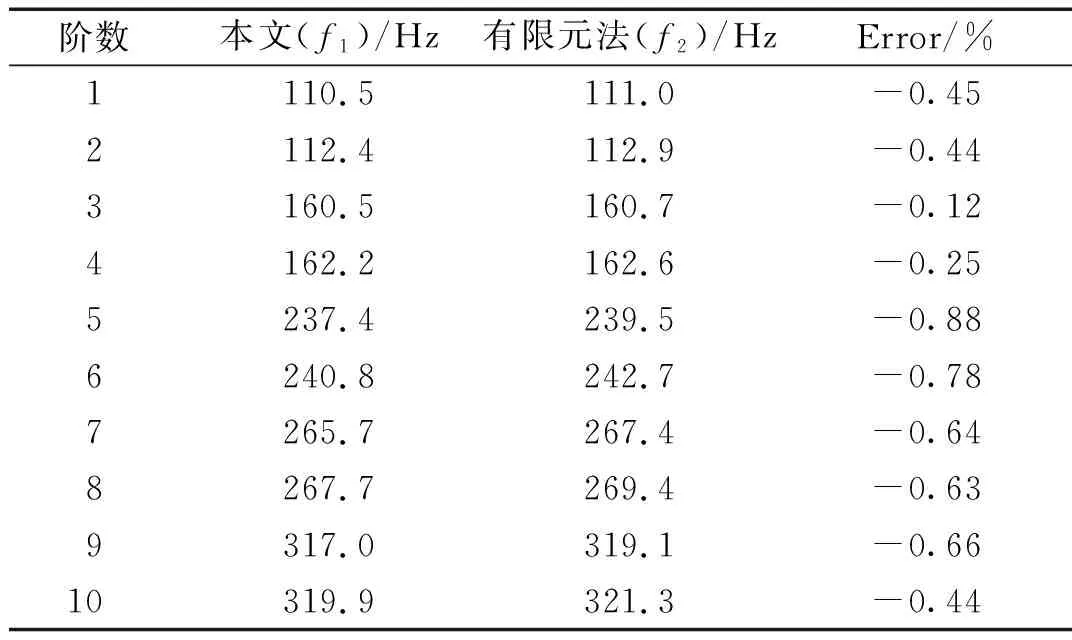
表6 当H=0时部分充液圆柱壳前10阶固有频率对比

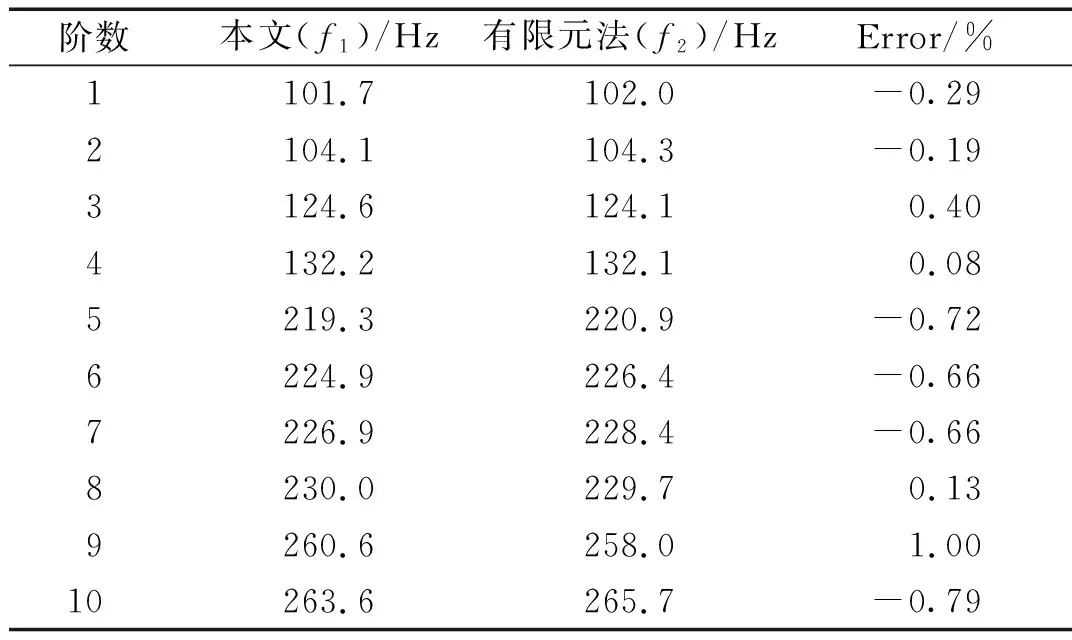
表7 当H=0.127 3 m时部分充液圆柱壳前10阶固有频率对比

为进一步说明本文方法的准确性，将本文方法计算的固有频率值与Amabili等的研究试验结果进行对比，如表8所示。(Amabili等研究模型参数如下：L=0.664 m，R=0.175 m，h=0.001 m，ρ=7 680 kg/m3，E=206 GPa，μ=0.3，ρf=1 000 kg/m3。)

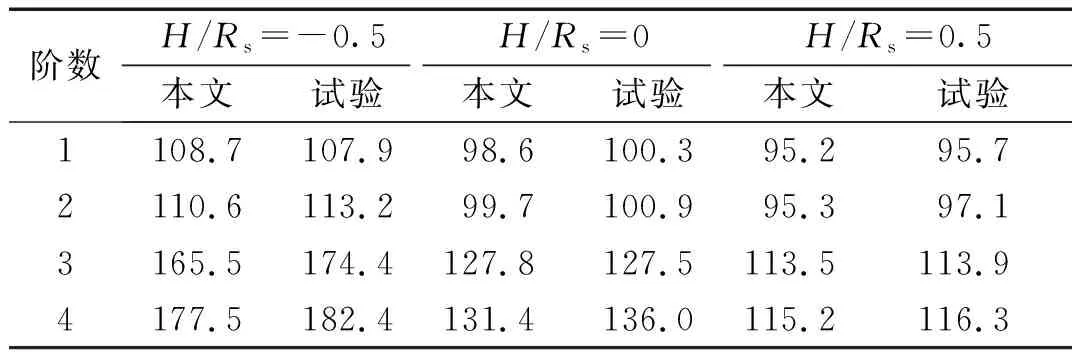
表8 不同充液高度下本文方法与试验结果频率对比

从表8可以看出，不同充液高度下解析法和试验方法得到的数据大体吻合良好，进一步说明本文方法的准确性。

4 部分充液与部分浸没工况对比分析

4.1 全充液与全浸没工况的对比

对于全充液圆柱壳或者无限域圆柱壳，当所研究的频率较低时，其同阶次的固有频率往往是比较接近的。主要原因是由于频率较低时对应的无量纲径向波数krRs比较小，根据贝塞尔函数小宗量展开的性质，内、外流场对应的流体负载在数学表达式上可认为近似相等[24]。

(24)

式中：m，n分别为轴向半波数和周向波数；Cmn为与流体相对位置(内流场或外流场)无关的量。此外式(24)中贝塞尔函数也可能取其他形式(比如第一类汉克尔函数和第一类贝塞尔函数)，此时式(24)依然可简化为约等号右侧形式。

本处简单说明一下式(24)中约等号右侧表达式是如何近似得到的。以内流场为例，当无量纲波数较小时，可对贝塞尔函数进行小宗量近似展开

(25)

式中：Γ(· )为伽马函数，且Γ(n+1)=n！。

根据式(25)可以得到如下表达式

(26)

据此可判断全充液或全浸没(无限域)时，二者对应的前几阶固有频率值应该十分接近。比如以第一阶固有频率为例，全充液时为97.9 Hz，全浸没时为98.9 Hz，差异很小。

4.2 部分充液与部分浸没工况的对比

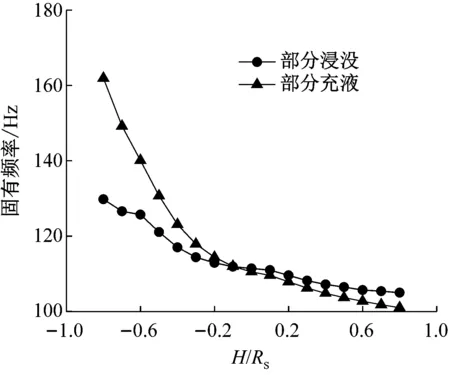
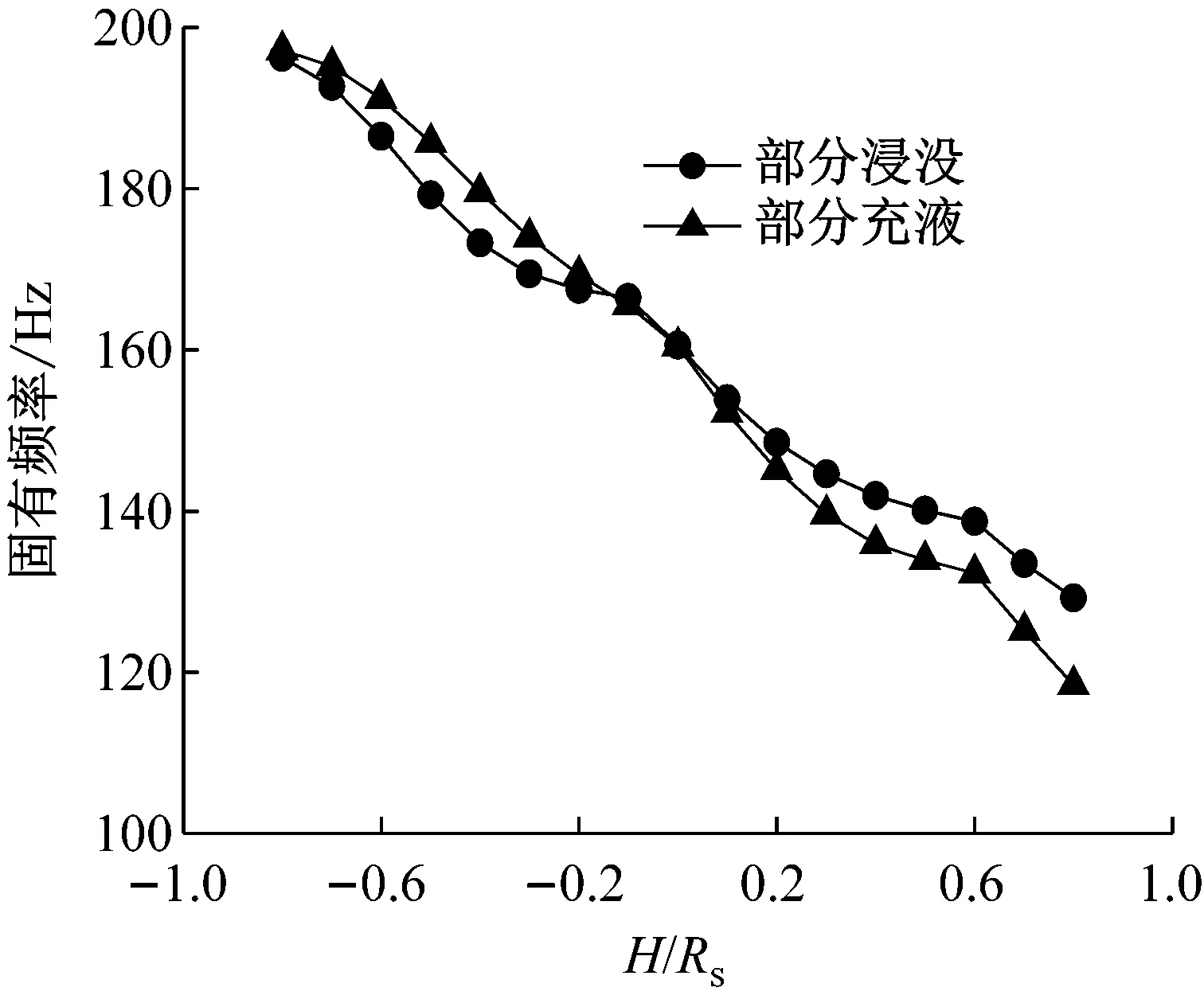
为了进一步了解部分耦合时内、外流场是否也有类似的性质，同时也为分析部分充液时固有频率随特征高度的变化规律，将无量纲特征高度H/Rs取值为-0.8～0.8，计算对应的第一、第三阶固有频率值，并与图6(部分浸没工况)中部分数据进行对比，结果如图8所示。

(a) 第一阶

(b) 第三阶

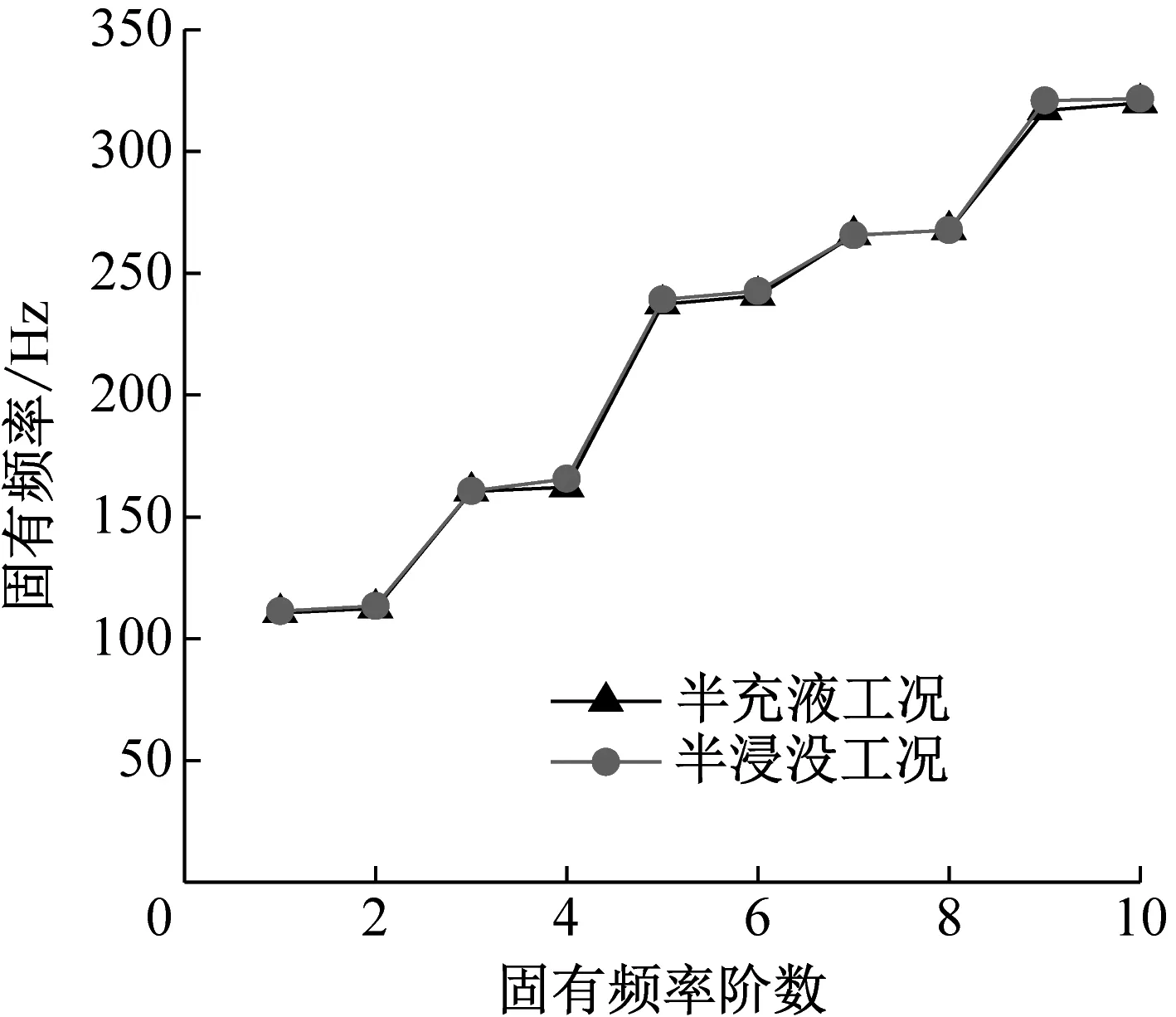
从图8可以看出，部分充液工况下固有频率随特征高度的变化规律与部分浸没时类似，即同阶次固有频率随液面的增高而降低且下降的速率无明显规律。此外，值得注意的是，半充液工况与半浸没工况下(H/Rs=0)同阶次固有频率值几乎相同。为了进一步证实这一规律，本文将半充液工况及半浸没工况下前10阶固有频率绘图比对，如图9所示。

从图9可以明显看出，无论是本文方法还是数值仿真，半浸没工况及半充液工况下前10阶固有频率值是几乎一致的。

4.3 数学机理分析

为了从数学机理上揭示和解释图9中规律的成因，可依据本文理论推导及借鉴贝塞尔函数的小宗量展开性质进行分析。

(a) 本文方法计算结果

(b) Nastran仿真计算结果

本处以半充液工况为例，满足α=β=0，且θ=φ+π/2。由于内、外流场的主要区别在于贝塞尔函数类型不同，且控制方程式(23)中仅有矩阵[Vp]和[Tp]与贝塞尔函数有关，故重点在于分析式(18)和式(21)。这里假设权函数为声压的周向展开函数，由此式(18)和式(21)可以改写为如下形式

(27)

(28)

当a≠b时，式(27)、式(28)中正弦三角函数积分为零，由此可判断矩阵[Vp]和[Tp]是对角矩阵，表达式如下

(29)

(30)

根据振动控制方程式(21)，仅与贝塞尔函数相关的矩阵可表示为[Tp] [Vp]-1，由此[Tp][Vp]-1也是对角矩阵

(31)

同理，半浸没工况时[Tp][Vp]-1也有类似性质，可推导出相同的近似表达式，这就从数学机理上阐述了为何半充液工况及半浸没工况下同阶次固有频率相近。换句话说，当圆柱壳处于半充液或半浸没状态时，流体负载可以近似简化为相同的数学表达式，从而导致同阶次固有频率十分接近。

此外，由于声压负载关于特征高度是连续函数，固有频率关于特征高度的函数曲线理论上也是光顺的，因此可以推断，在半充液或半浸没附近时，相同液面高度下部分充液与部分浸没对应的同阶次固有频率也是非常接近的。从图8可以大概看出，当H/Rs在-0.2～0.2内时，上述规律依旧存在。

为了更直观、充分地了解该规律，分别取H/Rs=-0.2和0.2，计算部分充液工况和部分浸没工况下前10阶固有频率，并开展对比研究，如图10所示。

(a) H/Rs=-0.2

(b) H/Rs=0.2

由图10可知，当H/Rs=-0.2和0.2时，部分充液和部分浸没工况下固有频率十分接近。说明在半浸没或半充液附近，内、外流场在等液面高度时同阶次固有频率具有一致性。这一规律对相关的工程问题有一定的指导价值，例如采用试验手段开展部分浸没(H/Rs在-0.2～0.2内)圆柱壳结构的模态试验时，可以通过内部充入等液面高度的相同流体来取得相近的试验效果。且由于外流场试验受到试验场地的限制，其难度会远高于内流场试验，采用内流场试验替代外流场试验即经济性又便利。

5 结 论

本文基于两套坐标系的建模思路以及Galerkin方法，提出了有限长部分浸没圆柱壳耦合振动的求解方法，并将该方法拓展到研究部分充液圆柱壳的耦合振动。此外，本文还对比分析了相同液面高度下，圆柱壳与内、外流场耦合振动频率的异同。具体结论如下：

(1) 本文方法的计算精度高且适用范围广，无量纲特征高度H/Rs可从-0.8取到0.8；此外，本文方法还具有计算量小的优势。

(2) 圆柱壳与流场部分耦合时，液面高度增大会导致湿表面增大，从而导致增加附连水质量，使得同阶次固有频率下降。

(3) 当圆柱壳处于半充液或半浸没附近时，相同液面高度下同阶次固有频率十分接近。这一规律对于实际的工程问题有指导意义，如可以通过部分充液圆柱壳模态试验来替代外流场试验。