RPC-CFST组合柱轴压性能试验研究

张仁巍， 曾武华， 庄一舟， 邓永新

(1. 三明学院 建筑工程学院， 福建 三明 365004; 2. 浙江工业大学 土木工程学院， 杭州 310023；3. 建研检测集团有限公司， 福建 三明 365000)

钢管混凝土(concrete-filled steel tube，CFST)组合柱是在钢管中填充素混凝土而形成，且由钢管与核心混凝土之间共同承担外荷载作用，其具有承载能力强、塑性和韧性好等特点，目前在大跨度桥梁、单层和多层厂房柱、高层和超高层建筑等工程中得到广泛应用[1-4]。此外，国内外学者以截面形式、钢管壁厚、套箍系数、长细比、偏心率和加载类型等参数对CFST组合柱开展了静力和抗震试验研究，深入探讨了CFST组合柱的受力机理、破坏形态、套箍效应和荷载-挠度曲线、应力分布等，在试验验证的基础上，进行了大量的数值建模分析，提出了CFST组合柱的轴压、偏压承载力实用算法和恢复力模型计算方法等[5-9]。

虽然CFST组合柱具有优越的承载力、变形能力强等优点，但目前仍然存在一些有待解决的问题：一方面是CFST组合柱因钢管外露，钢管易被腐蚀，造成组合柱的耐久性明显降低[10-11]；另一方面是CFST组合柱在轴向荷载作用下，容易发生局部屈曲破坏，造成高性能钢管难以发挥作用[12]；此外，当钢管外部温度超过一定值时，钢管对核心混凝土的套箍效应明显降低，导致组合柱的承载力迅速下降，实际工程中需要对其进行防腐和防火处理，特别是在大跨度桥梁，海洋环境腐蚀严重，造成后期维护成本高，存在诸多不可预见的风险[13]。因此，本文提出采用活性粉末混凝土(reactive powder concrete，RPC)外包钢管混凝土柱，形成RPC-CFST组合柱。与CFST柱相比，RPC-CFST组合柱采用强度高、耐腐蚀和抗渗能力强的RPC[14-15]，能显著提高组合柱的承载力、耐久性和抗火性能等，从全寿命降低造价的角度，其优势明显。然而，目前对RPC-CFST组合柱的轴压性能研究鲜有报道，有必要对其开展轴压试验研究，深入分析该类组合柱的力学性能影响。

综上分析，本文以RPC厚度、长细比为参数，对RPC-CFST组合柱开展轴压性能试验研究，分析RPC-CFST组合柱的受力全过程、荷载-轴向位移曲线、紧箍效应和极限承载力等。借助ABAQUS有限元软件，建立经试验验证的有限元模型，同时拓展参数分析。在试验研究和有限元分析的基础上，结合钢管混凝土结构技术规范和规程，提出RPC-CFST组合柱的实用算法，研究成果对该类组合柱的推广应用具有重要的指导意义。

1 试验概况

1.1 试件设计与制作

为研究RPC-CFST组合柱的轴压性能，以RPC厚度、长细比为主要变量，共设计了5根RPC-CFST组合柱，具体如表1所示。各试件的外径和钢管厚度分别为180 mm，4 mm，表1中CFST-0-3试件编号的含义为：“CFST”为对照组的钢管混凝土；“0”为RPC厚度为0；“3”为试件的高度为300 mm。同理，RPC-10-3试件编号的含义为：“RPC”为RPC-CFST组合柱的外层RPC；“10”为RPC厚度为10 mm；“3”为试件的高度为300 mm，其余试件的编号以此类推，试件的截面形式及尺寸如图1所示。

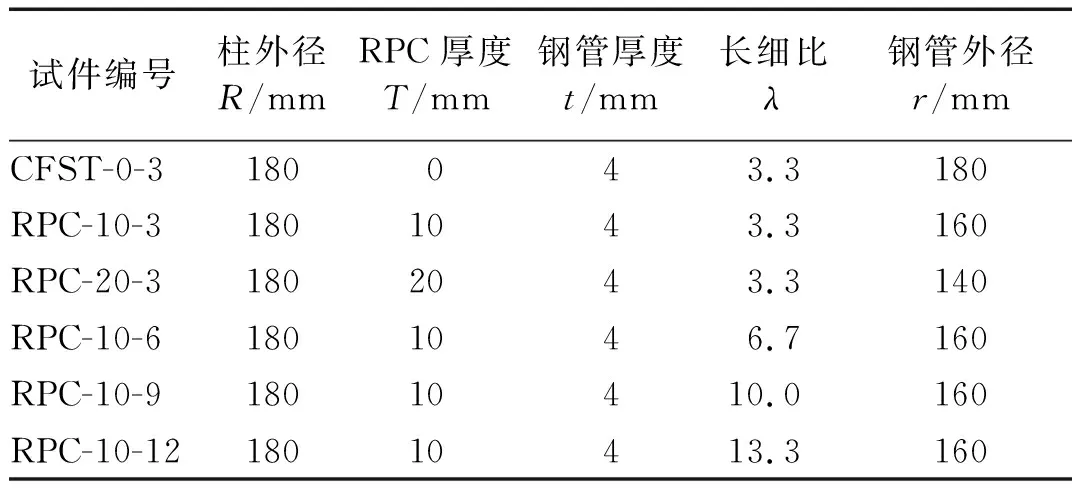
表1 试件设计参数

(a) CFST-0-3

1.2 材料参数

组合柱的钢管采用型号为Q235的钢材，依据GB/T 228.1—2010《金属材料 拉伸试验》[16]的试验方法，实测得到钢材屈服强度为307.6 MPa，极限强度为442.8 MPa，弹性模量为195.0 GPa，泊松比为0.3。钢管内部混凝土的配合比，如表2所示，RPC配合比(其中钢纤维的体积掺量为1%)如表3所示。依据GB/T 50081—2019《混凝土物理力学性能试验方法标准》[17]和GB/T 31387—2015《活性粉末混凝土》标准[18]分别测得C30和RPC的材料性能，如表4所示。

表2 C30配合比

表3 RPC配合比

1.3 试验加载与测点布置

试验采用5 000 kN的微机控制电液伺服万能压力机进行加载，具体如图2(a)所示。正式加载前先进行预加载，即施加预估极限承载力的10%，目的在于检测试验设备是否正常工作和判断试件是否处于偏心受压情况。此后进入正式加载，试验采用分级加载，每级达到预估极限承载力的10%时停止35 s，便于观察试验现象和检测数据；当荷载达到预估极限承载力的80%后，采用位移控制的加载方式，加载速度为0.15mm/min，直到荷载降低至极限承载力的70%左右，停止试验。浇筑外层RPC时，提前在钢管外表面的中部4个侧面上粘贴应变测点。在试验加载前，沿着RPC-CFST组合柱的4个侧面布置混凝土应变测点，正式加载时在试件的两侧布置两个位移计，具体如图2(a)、图2(b)所示。

表4 混凝土材料性能

(a) 试验加载实景

2 试验结果与分析

2.1 破坏过程与形态

RPC-CFST组合柱的破坏过程较为相似，受力过程如下：在加载初期，因轴向压力较小，RPC、钢管和内部混凝土之间协调工作，组合柱未见明显变化；随着轴向压力的不断增大，RPC-CFST组合柱内部的钢纤维被拉断而发出响声；当荷载达到极限承载力的75%时，组合柱在最薄弱位置开始出现细小裂缝，伴随着RPC小碎块地掉落，且响声不断增多；随着轴向压力的持续增加，钢管开始屈服，组合柱的竖向裂缝不断沿着两端发展，并造成RPC应变片出现断裂，而RPC小碎块掉落的越来越多；当荷载达到极限承载力时，因内部混凝土出现体积膨胀，钢管开始出现鼓曲，外层RPC因钢纤维大面积被拉断而发生大响声，外层RPC随即出现一条较大的竖向裂缝；此后，组合柱的轴向压力主要由CFST承担，外层RPC主要承担环向作用力；当荷载下降至极限承载力的70%时，停止加载。各试件的最终破坏形态，如图3所示。

(a) CFST-0-3

(d) RPC-10-6

2.2 荷载-轴向位移曲线

各试件的荷载-位移曲线，如图4所示。由图4(a)可知：在加载初期，各试件处于弹性阶段，荷载-位移曲线基本呈现线性关系；当荷载达到极限承载力的75%时，外层RPC开始出现细小裂缝，与CFST-0-3试件相比，RPC-CFST组合柱更早进入弹塑性阶段，但二者在下降阶段的曲线基本重合；结合表5可知，在相同截面下，当钢管混凝土外层采用10 mm的RPC时，组合柱的极限承载力仅提高1.42%，提升幅度小，但从材料的使用上看，组合柱的耐久性显著提高；此外，将外层RPC从10 mm增大至20 mm，组合柱的极限承载力提高了4.67%，从荷载-轴向位移曲线可以看出，RPC-20-3试件的刚度明显提升，但弹塑性阶段不明显，试件在达到极限承载力后，荷载-轴向位移曲线出现急剧下降的趋势，且延性降低，分析原因可知，因RPC厚度增大，钢纤维含量提高，外层RPC能够承担的轴向压力增强，使得组合柱的刚度提升，但RPC属于脆性材料，当外层RPC开始出现裂缝后，易造成局部范围内的钢纤维被群体拉断，从而出现较宽的裂缝(见图3中的竖向裂缝)，即荷载-轴向位移曲线出现较明显的陡降现象，所以工程中应当严格控制外层RPC厚度。

由图4(b)可知：不同长细比的RPC-CFST组合柱均有弹性阶段、弹塑性阶段和下降阶段；因轴向压力小，在弹性阶段RPC-CFST组合柱的荷载-轴向位移曲线基本呈线性变化，但随着长细比的增加，弹性刚度逐渐降低，是因长细比越大，组合柱试件重心越高，试件更易发生纵向弯曲，即整体性能下降；在弹塑性阶段，因外层RPC的裂缝不断出现，曲线开始出现波动，当RPC内部钢纤维被群体扯断时，组合柱达到极限状态，荷载开始降低；在下降阶段，由于RPC受损，仅依靠CFST承担轴向力，荷载缓慢降低，即曲线较为平缓；结合表5可知，当长细比从3.3增加至13.3时，组合柱的极限承载力降低了11.48%。

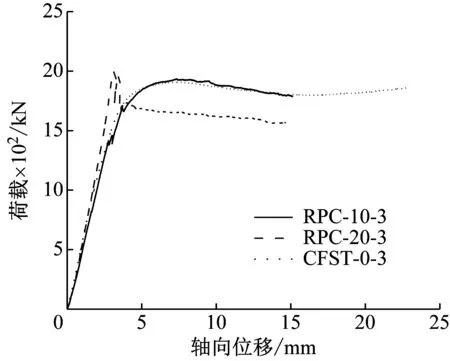
(a) 不同RPC厚度的荷载-轴向位移曲线

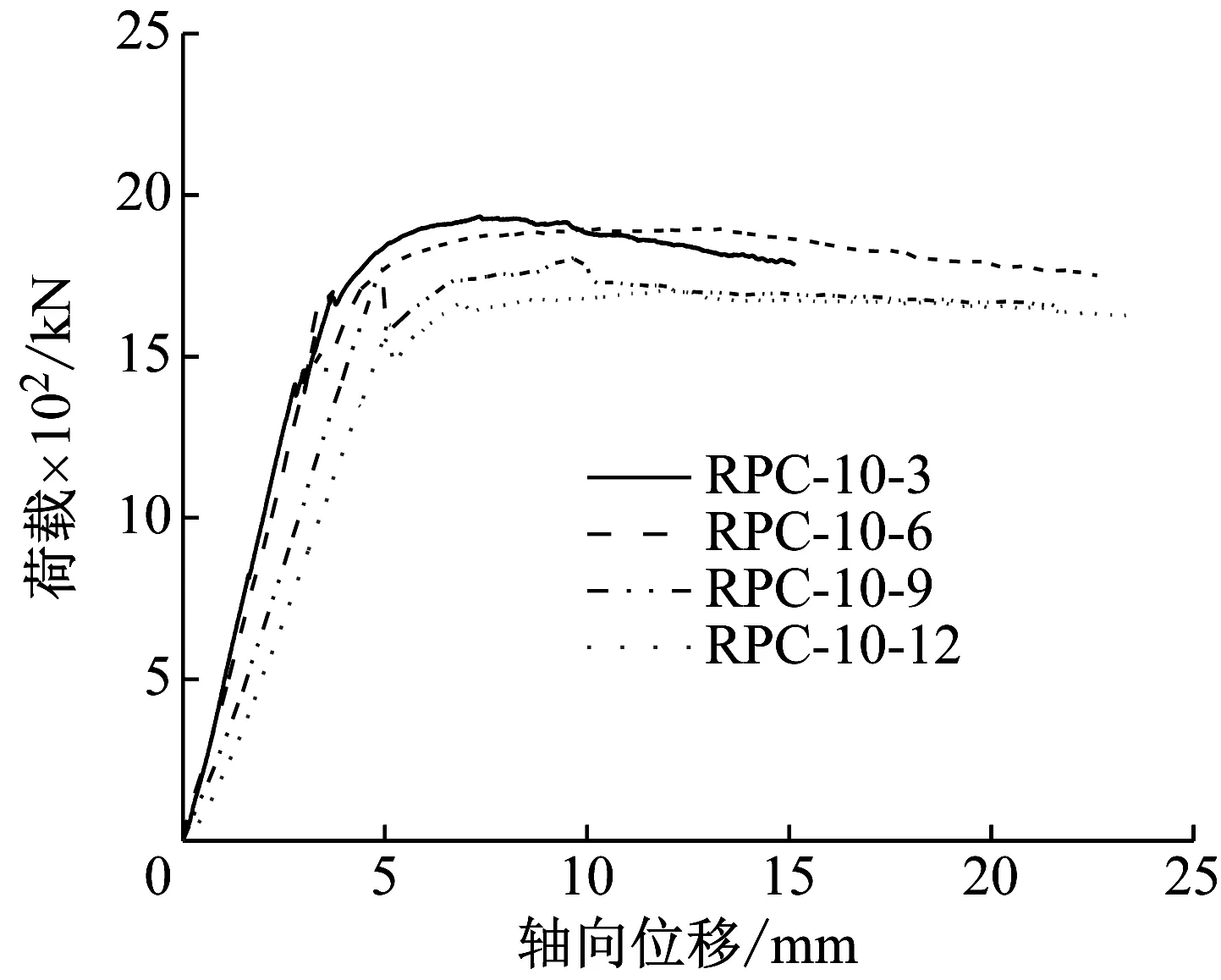
(b) 不同长细比的荷载-轴向位移曲线

表5 试验结果

2.3 荷载-环向应变曲线

不同RPC厚度和长细比的荷载-环向应变曲线，如图5所示。图5中应变取各试件钢管中部截面4个测点的平均值。由图5可知：试件在加载前期，曲线基本重合，即试件处于弹性状态；随着轴向压力的不断增大，曲线斜率不断降低，即试件进入弹塑性阶段，RPC、钢管和内部混凝土之间的相互作用明显增强，应变快速增长；最终因钢管内部混凝土受到挤压，体积不断膨胀，钢管开始出现鼓曲，外层RPC内的钢纤维不断被拉断而出现裂缝，组合柱达到极限承载力；在下降阶段，曲线的斜率基本不变。

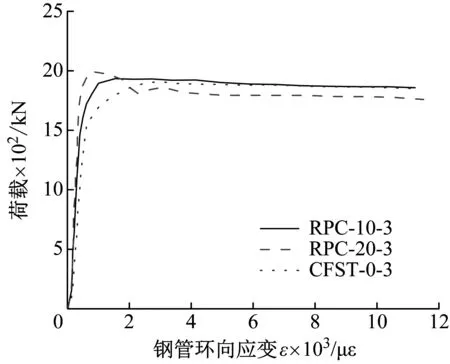
(a) 不同RPC厚度

(b) 不同长细比

2.4 套箍效应分析

为研究外部RPC是否对CFST起到套箍效应，取材料泊松比为研究对象，即中截面RPC环向应变和竖向应变的比值(取绝对值)，RPC泊松比为0.19，当材料泊松比超过0.19时，即认为外部RPC对CFST起到套箍效应。试验测得的荷载-泊松比曲线，如图6所示。

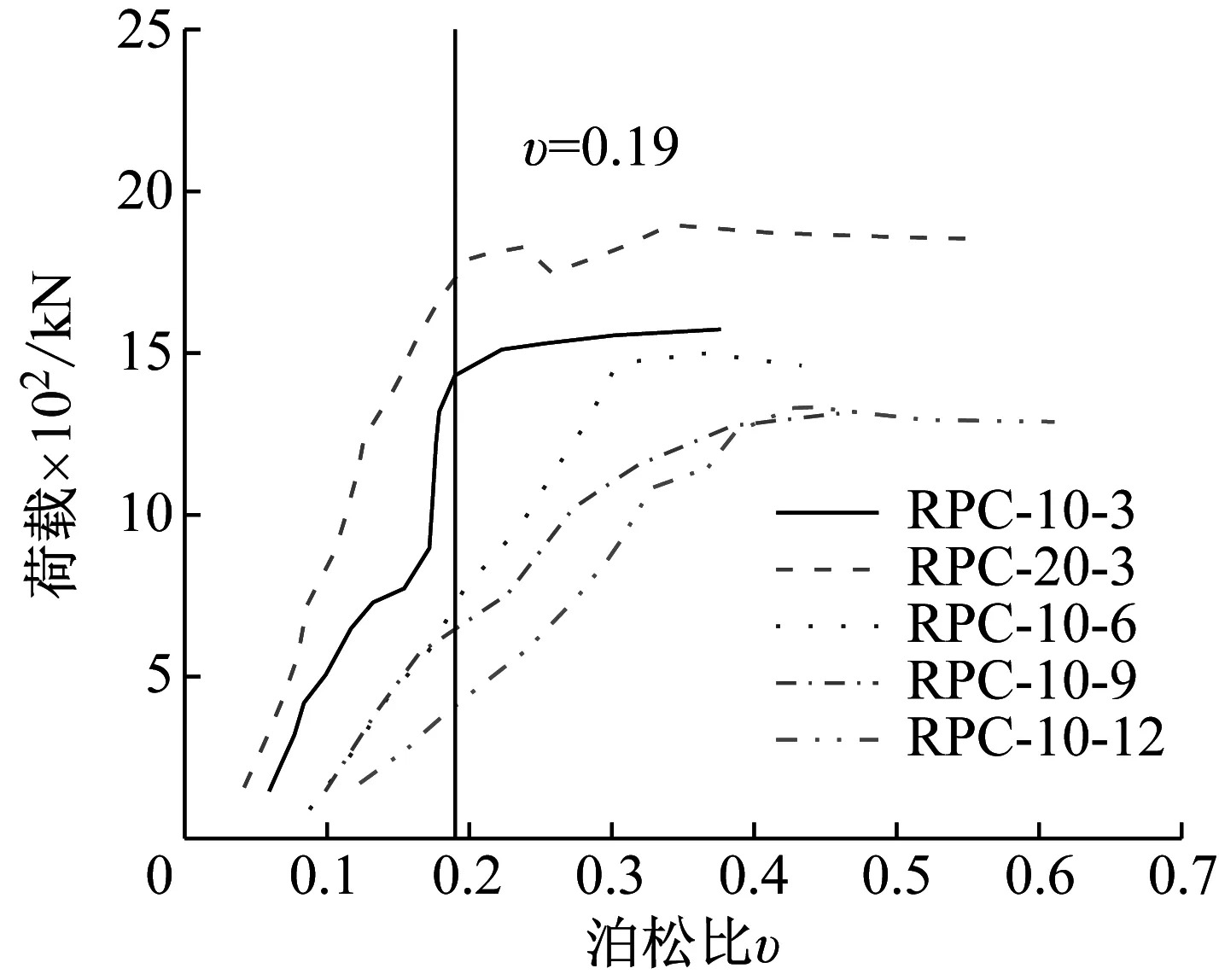
图6 荷载-泊松比曲线

由图6可知：在加载初期，各试件的材料泊松比均小于0.19，说明外层RPC未对CFST起到套箍效应；随着轴向压力不断增大，各试件的材料泊松比明显提高；当外层RPC从10 mm(RPC-10-3)增大至20 mm(RPC-20-3)时，外层RPC对CFST起到的套箍效应更迟，是因为提高RPC厚度，RPC-CFST组合柱的刚度提升，即外层RPC能够承担更多荷载，因此外层RPC对CFST柱起到的套箍效应越迟。由图6还可知，随着长细比从3.3(RPC-10-3)增大至13.2(RPC-10-12)，外层RPC对CFST起到的套箍效应出现的更早，原因在于提高组合柱长细比，使得结构刚度降低，试件更早进入弹塑性阶段，即外层RPC更早对CFST柱起到套箍效应。

3 有限元分析

因试验参数有限，为进一步分析不同参数对RPC-CFST组合柱受力性能的影响规律，本文在试验研究的基础上，采用ABAQUS软件程序建立有限元模型，同时开展参数分析。

3.1 有限元建模简介

采用ABAQUS软件建立RPC-CFST组合柱的有限元模型，模型包括三部分：即外层RPC、钢管和核心混凝土。有限元模型如图7所示。外层RPC和核心混凝土均采用八节点三维实体减缩积分单元(C3D8R)，对于钢管，研究者们有采用壳单元(C3D4)，也有采用八节点三维实体减缩积分单元(C3D8R)，而采用壳单元经常会出现不收敛和网格不易划分等问题，因此本文采用C3D8R单元来模拟钢管，即计算过程更高效和易收敛[19]。

RPC受压、受拉应力-应变本构关系采用文献[20]和文献[21]的研究，其中材料参数选用实测值(见表4)；钢管应力-应变关系采用材性试验值；核心混凝土本构关系采用文献[22]提出的关系式。外层RPC与钢管之间采用surface to surface contact，即有法向和切向两个方向，法向方向采用硬接触，切向方向采用库伦摩擦模型[23]，摩擦因数取0.28；钢管与核心混凝土之间同样采用surface to surface contact，摩擦因数取0.5[24]。各试件的网格大小均为20 mm，完全约束组合柱的底端自由度，组合柱顶端的两个方向不施加约束，仅在组合柱顶端施加轴向压力。

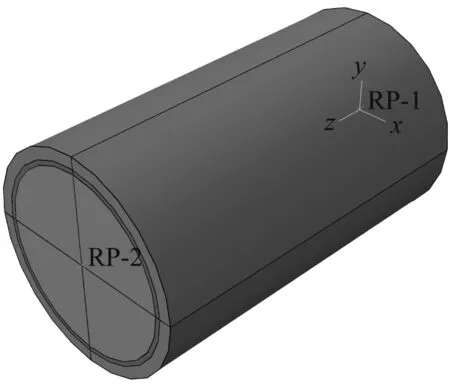
(a) 标准模型

3.2 有限元模型验证

对6根试验试件开展了数值建模分析，有限元计算得出的荷载-轴向位移曲线与试验曲线对比，如图8所示。由图8可知，有限元计算曲线在弹性段、弹塑性阶段和下降段均吻合良好。

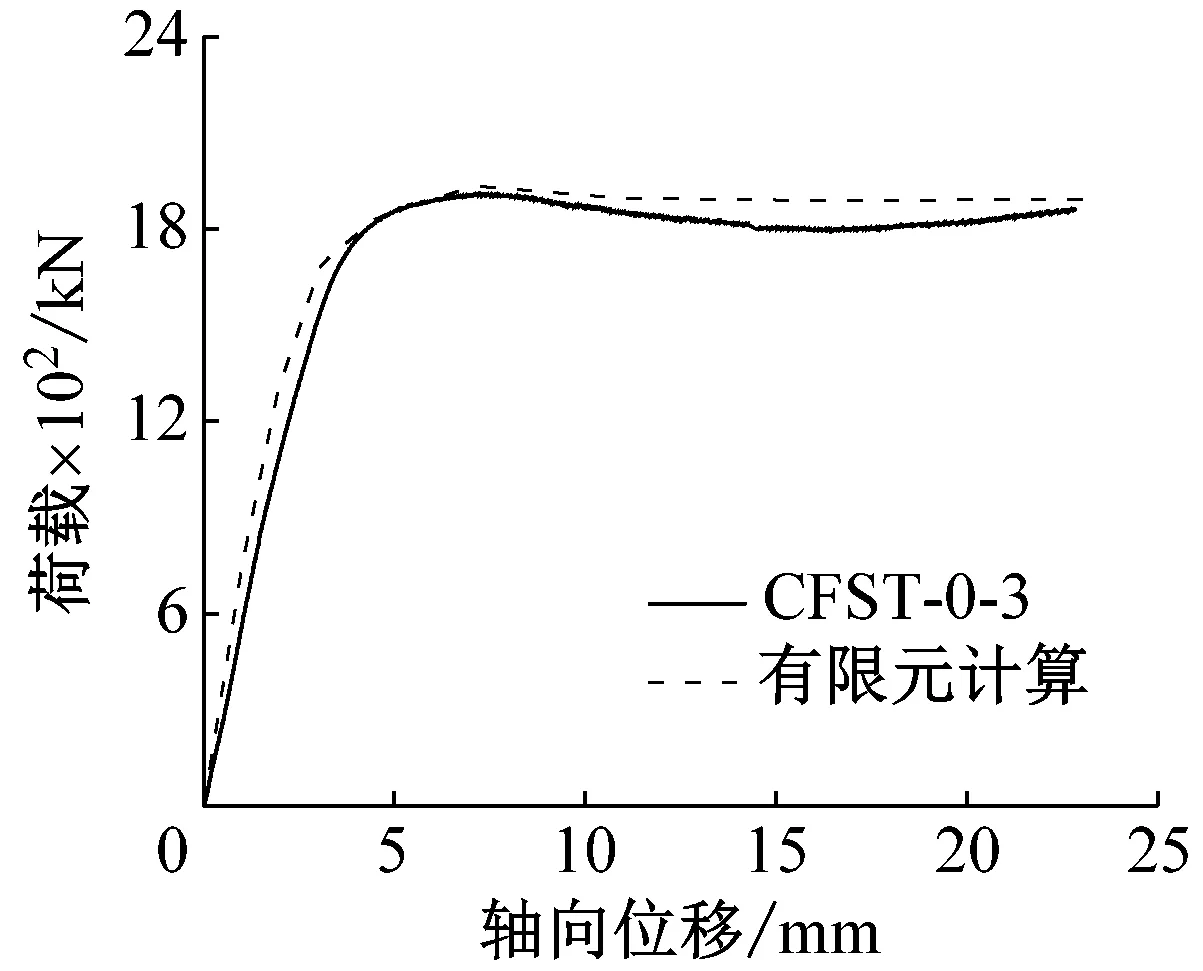
(a)CFST-0-3

(d) RPC-10-6

有限元计算值与试验值的对比，如表6所示。由表6可知，有限元计算的极限承载力与试验值之比的平均值为1.010，均方差为0.009，说明采用本文建模方法能够准确分析RPC-CFST组合柱的轴压受力性能，可用于后期有限元参数计算。

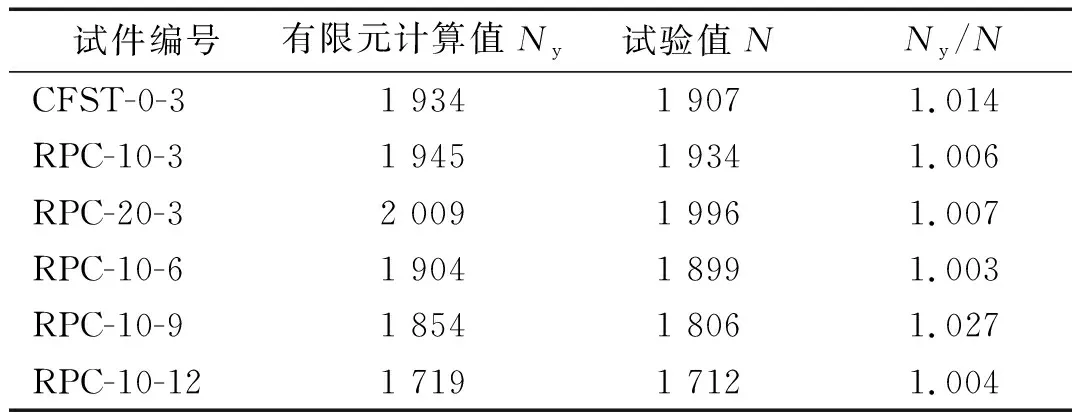
表6 有限元计算值与试验值对比

3.3 参数拓展分析

借助有限元软件计算了径厚比、RPC强度、含钢率、混凝土强度、钢管强度等级和套箍系数等参数对RPC-CFST组合柱的轴压性能影响，其荷载-轴向位移曲线如图9所示。

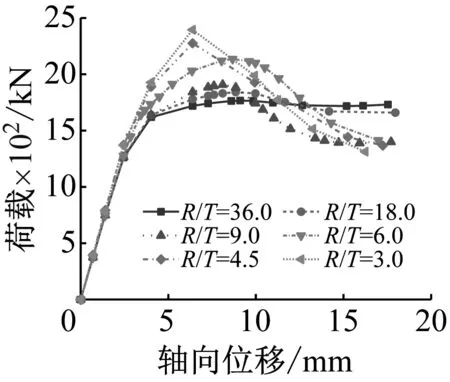
(a) 径厚比

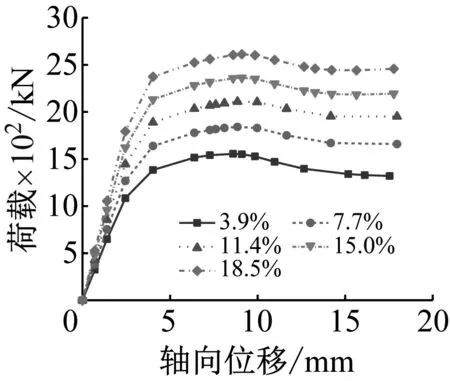
(c)含钢率

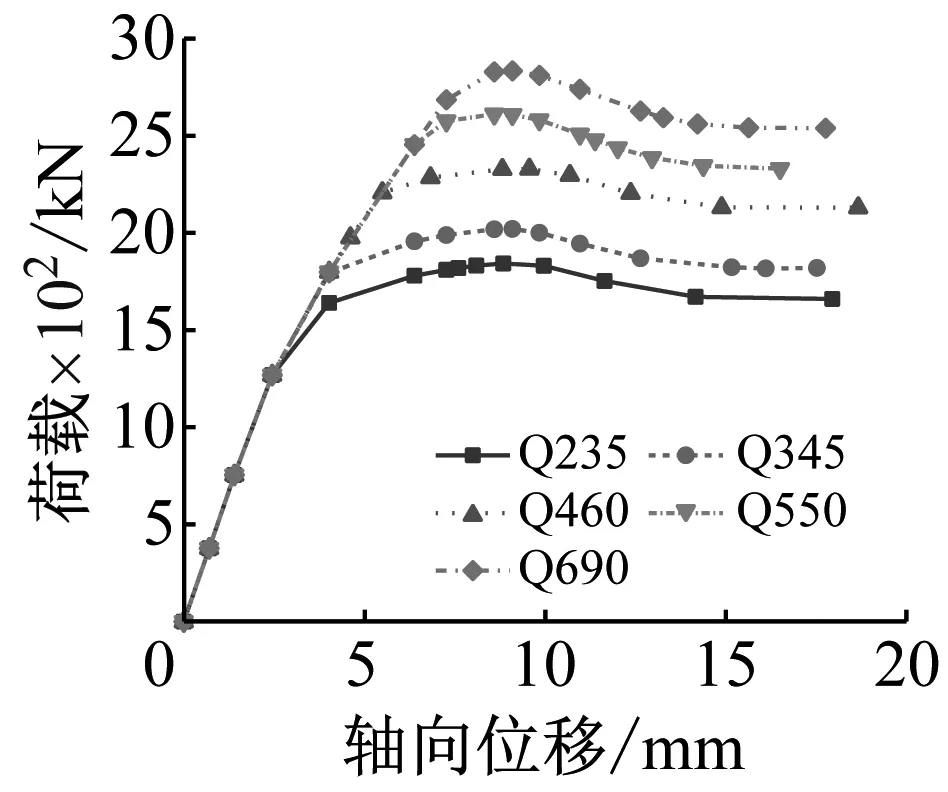
(e) 钢管强度等级

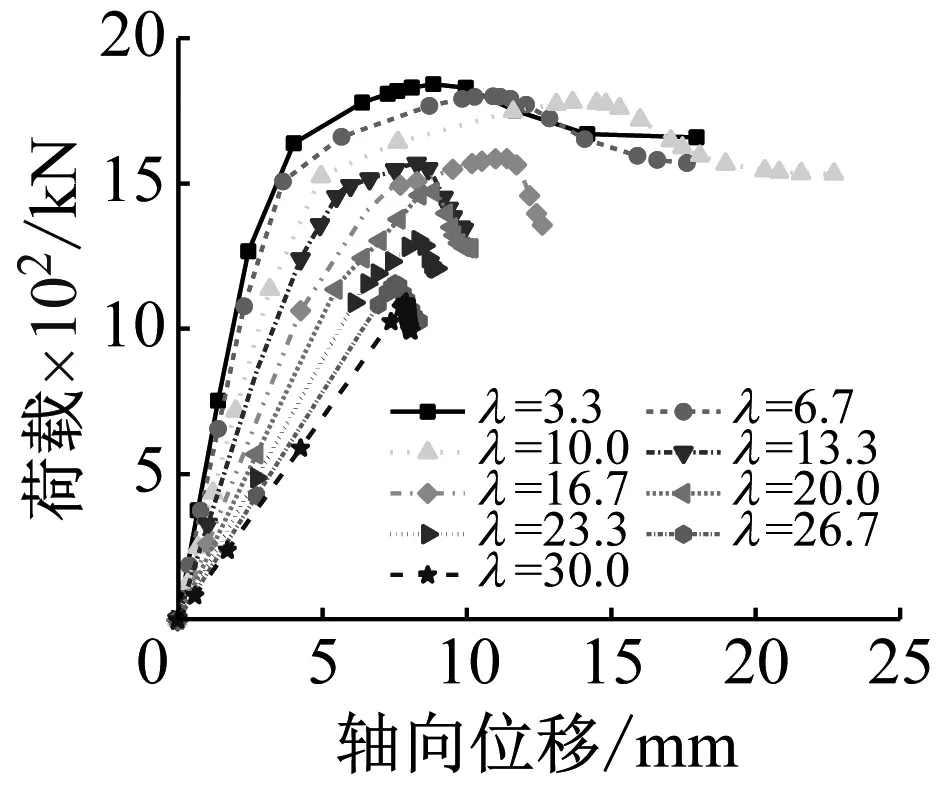
(g) 长细比

3.3.1 径厚比

图9(a)为组合柱不同径厚比(R/T)的荷载-轴向位移曲线。由图9(a)可知：随着径厚比降低，组合柱在弹性刚度段基本重合，极限承载力明显提高；因UHPC(ultra-high performance concrete)厚度增加，其脆性特征更为凸出，下降段斜率明显增大，即延性降低，因此实际工程中建议径厚比取6～18。

3.3.2 RPC强度

图9(b)为组合柱不同RPC强度的荷载-轴向位移曲线。由图9(b)可知，不同RPC强度的荷载-轴向位移曲线之间较为接近，当RPC强度从100 MPa提升至140 MPa时，极限承载力仅提高了5.8%，弹性刚度和下降段曲率变化不显著。综合考虑，实际工程中RPC强度根据需求即可。

3.3.3 含钢率

图9(c)为组合柱不同含钢率的荷载-轴向位移曲线。由图9(c)可知，当钢管厚度从2 mm增大至10 mm(含钢率从3.9%增大至18.5%)时，组合柱的弹性刚度、极限承载力和延性性能随着含钢率的提升而逐渐提高，含钢率的增加意味着钢管截面抗压刚度得到提升，其能抵抗变形的能力增强，但考虑经济性等因素，建议工程中含钢率取3.9%～11.4%。

3.3.4 混凝土强度

图9(d)为组合柱不同混凝土强度的荷载-轴向位移曲线。由图9(d)可知：随着混凝土抗压强度的增加，组合柱的弹性刚度变化不显著，但极限承载力不断均匀提升；高强度混凝土试件往往延性差，但从曲线可以看出，该组合柱的延性并未降低，原因在于外部RPC和钢管对内部混凝土起到套箍效应，提升了内部混凝土的延性，实际工程中建议混凝土强度等级取为C30～C50。

3.3.5 钢管强度等级

图9(e)为组合柱不同钢管强度等级的荷载-轴向位移曲线。由图9(e)可知，增强钢管强度等级对其弹性刚度影响不大，而极限承载力显著提高，即增强钢管强度等级时，其对核心混凝土的套箍作用更强，与外层RPC强度的匹配度更高，使得组合柱的整体性能好，但延性变化不明显，因此实际工程中建议采用Q235～Q345。

3.3.6 套箍系数

钢管套箍系数反映组成钢管混凝土截面的钢材和核心混凝土的几何特性和物理特征影响，用ζ表示，即套箍系数越大，钢材所占比重越大，钢管可对核心混凝土提供足够的约束作用，计算公式见式(1)。

ζ=Asfy/Acfc

(1)

式中：As为组合柱钢管截面面积；Ac为组合柱内部混凝土截面面积；fy为钢管屈服强度；fc为混凝土抗压强度。

图9(f)为组合柱不同套箍系数的荷载-轴向位移曲线。由图9(f)可知，当套箍系数从0.300增大至2.849时，组合柱的弹性刚度和极限承载力均先增大后降低，当套箍系数超过一定值时，其对组合柱的套箍效应逐渐降低，因此工程中建议该类组合柱的套箍系数取0.875～1.850。

3.3.7 长细比

图9(g)为组合柱不同长细比的荷载-轴向位移曲线。由图9(g)可知：随着长细比的增加，组合柱的弹性刚度和极限承载力明显降低，即稳定性能不断下降；当长细比小于6时，曲线波动不明显；当长细比大于16时，组合柱的弹性刚度和极限承载力的下降幅度明显增大，且延性降低，因此实际工程中建议长细比取6～16。

4 承载力计算模型

RPC-CFST组合柱属于一种新型组合柱，目前对其承载力计算公式未有明确计算模型，因此有必要对该类组合柱的承载力计算方法进行探讨分析。

从有限元分析并结合试验结果可知，当RPC-CFST组合柱达到极限承载力时，钢管出现屈服的现象均发生在组合柱达到极限承载力前，但钢管仍然受到轴向荷载且套箍效应逐渐凸显，而外层RPC与CFST之间的接触应力较小，相互作用不明显，因此可以采用简单叠加法计算外层RPC与CFST之间的承载力，计算公式如下

Nu=Nrpc+βNcfst

(2)

Nrpc=Arpcfrpc

(3)

式中：Nu为组合柱的极限承载力；Nrpc为外部RPC承担的承载力；Ncfst为钢管混凝土承担的承载力，因外层RPC与组合柱之间未能同步达到极限承载力，因此在Ncfst前乘上折减系数β；frpc为RPC的轴心抗压强度；Arpc为RPC截面面积。

根据GB 50936—2014《钢管混凝土结构技术规范》[25]的单肢钢管混凝土柱在单一受力状态下的承载力计算方法可知，内部钢管混凝土的承载力Ncfst计算公式如下

Ncfst=Acfstfcfst

(4)

fcfst=(1.212+Bζ+Cζ2)fc

(5)

α=As/Ac

(6)

ζ=αfy/fc

(7)

式中：Acfst为钢管混凝土截面面积；fcfst为钢管混凝土抗压强度设计值，MPa；α为钢管混凝土试件的含钢率；B，C为截面形状对套箍效应的影响系数，当截面为圆形时，B，C影响系数的计算公式为

B=0.176f/213+0.974

(8)

C=-0.104fc/14.4+0.031

(9)

式中，f为钢管抗压强度设计值。通过有限元参数分析计算出的28根RPC-CFST组合柱极限承载力，可以得出每根试件CFST承载力的折减系数β，如表7所示。由表7可知，折减系数基本在1附近波动，因此偏安全取0.98，则RPC-CFST组合柱的极限承载力计算公式为

Nu=Nrpc+0.98Ncfst

(10)

此外，实际工程中还应考虑长细比对RPC-CFST组合柱极限承载力的影响。借鉴CECS 28—2012《钢管混凝土结构技术规程》[26]中的钢管混凝土柱考虑长细比影响的承载力稳定系数φl，其计算公式为

当H/R>4时

(11)

当H/R≤4时

φl=1

(12)

式中：H为柱的等效计算长度；R为柱的外直径。

表7 折减系数β

公式计算的稳定系数值和有限元分析值的对比曲线，如图10所示。通过公式计算得出的RPC-CFST组合柱的承载力稳定系数与有限元计算得到的稳定系数之比的平均值为1.001，均方差为0.074，结合图10可知，二者曲线较为接近，说明CECS 28—2012《钢管混凝土结构技术规程》中的钢管混凝土柱考虑长细比影响的承载力稳定系数φl适用于RPC-CFST组合柱，且准确度高。综上分析，RPC-CFST组合柱的承载力计算公式为

Nu=φl(Nrpc+0.98Ncfst)

(13)

公式计算的极限承载力与试验值，如表5所示。二者之比的平均值为0.96，均方差为0.06，说明本文提出的RPC-CFST组合柱的极限承载力计算公式具有高精度，可应用于工程实际。

图10 折减系数对比

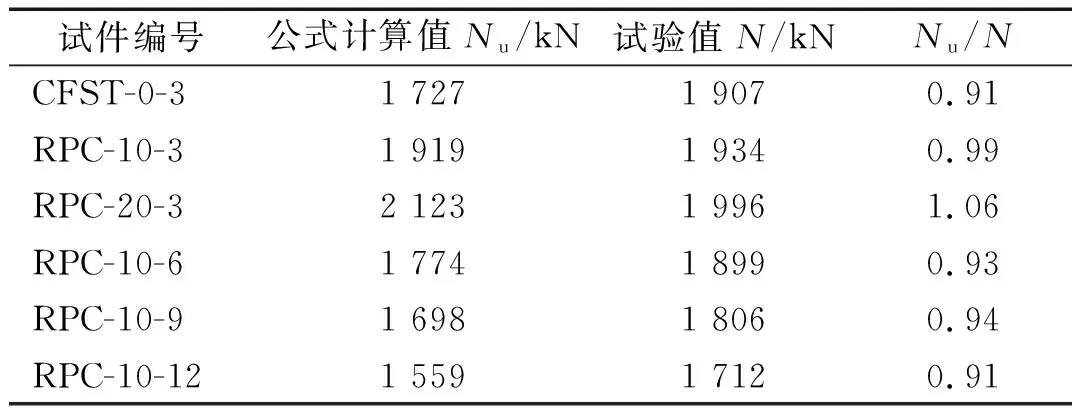
表5 试件公式计算值与试验值之比

5 结 论

(1) 在加载前期，RPC、钢管和核心混凝土之间协同工作；当荷载达到极限承载力的75%后，因内部核心混凝土膨胀，钢管鼓曲，外部RPC内的钢纤维被群体拉断，组合柱出现一条肉眼可见的竖向裂缝，不同参数的RPC-CFST组合柱受力过程和最终破坏形态均较为接近。

(2) 随着RPC厚度从10 mm增加至20 mm，RPC-CFST组合柱的极限承载力提高了4.67%；随着长细比从3.3增大至13.3，RPC-CFST组合柱的极限承载力降低了11.48%。

(3) 有限元参数分析表明，径厚比、含钢率、混凝土强度、钢管强度等级、套箍系数和长细比是影响RPC-CFST组合柱的重要参数，工程中建议该类组合柱的径厚比取6～18、含钢率取3.9%～11.4%、混凝土强度等级取C30～C50、钢筋强度等级取Q235 ～Q345、套箍系数取0.875～1.850、长细比取6～16。

(4) 在试验研究和有限元分析结果的基础上，借鉴钢管混凝土结构技术规范和规程，提出了可供工程应用的RPC-CFST组合柱轴压承载力实用算法，公式计算值与试验值吻合良好。