具有高静低动刚度特性的浮置板隔振器设计方法研究

刘 韦， 朱光楠， 杜香刚， 肖俊恒， 杨 军, 江 成

(1. 中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081；2. 株洲时代新材料科技股份有限公司, 湖南 株洲 412007； 3. 哈尔滨工业大学 航天学院, 哈尔滨 150001；4. 中国铁道科学研究院集团有限公司 高速铁路轨道技术国家重点实验室, 北京 100081;5. 清华大学 机械工程系, 北京 100084; 6. 北京铁科首钢轨道技术股份有限公司, 北京 102206)

随着我国城市化进程的加快，地铁引起的环境振动问题越来越受到人们的重视。针对地铁列车运行对环境的影响问题，国内外专家学者做了大量的工作，并取得了一定的研究成果，但大多针对振动中的中高频部分，很少涉及到低频部分[5-6]。近年来，地铁引发的低频(≤20 Hz)振动对周围环境的影响备受国内外学者关注[7-9]，振动中的低频部分由于频率低、波长相对较长，穿越地层以及建筑物的能力强，给附近居民的身心健康、工作和日常生活带来不良影响，有的甚至会损害古建筑物，影响精密仪器和高技术设备的正常运行。

频率较低的地面振动通常容易被人体所感知，低频振动由于波长较长，难以对其进行被动控制，这样就需要对振源加以控制。目前，在众多轨道减振措施中，浮置板轨道结构被认为是减振效果最好的轨道减振形式。但是，研究表明，钢弹簧浮置板轨道对于20 Hz以上的常规频段振动有明显的减振效果，但对于地铁低频振动来说，它的减振效果并不理想，在低频段甚至会出现振动放大现象。该频率恰恰与建筑构件的自振频率重叠。因此，传入建筑物内的振动容易和建筑构件发生共振，引发低频振动放大，进一步导致二次噪声的产生，对建筑物内人们的生活和工作造成影响。

钢弹簧浮置板轨道是典型的线性隔振系统，无法同时获得较低的起始隔振频率和较高的静态承载能力(系统稳定性)，因此浮置板轨道系统在获得高隔振效果的同时必然会引起轮轨系统振动响应增大，即浮置板轨道是通过牺牲系统的稳定性来换取高隔振效果。目前特殊减振地段会存在轮轨噪声大、车内噪声大、轨道结构振动大、车辆晃动、运营病害较多等问题。

目前，随着振动控制要求的不断提高，基于非线性理论的隔振技术的研究和应用越发广泛[10-12]，非线性系统可以通过自身阻尼非线性和刚度非线性来改善系统本身的隔振性能[13-15]。非线性隔振技术可以根据系统激励及振动特点进行最优参数的设计[11]，因此，利用非线性被动隔振技术提高轨道隔振性能、改善现有线性隔振系统存在的问题，是城市轨道交通减振轨道设计的重要方向。在非线性隔振技术中，高静低动刚度的隔振方式因其具有高的静载支承能力和低频隔振性能以及抗冲击保护的能力而逐渐引起人们的关注。具备高静低动刚度特性的隔振器具有随压缩量变化的刚度，在零负载时，隔振器具有较大静刚度(承载刚度)以确保高承载能力和小静态位移，当负载压缩隔振器至静平衡位置时，隔振器动刚度大幅降低，因此该类隔振器兼顾高承载能力和低固有频率，有效解决了被动隔振的瓶颈问题。

传统浮置板轨道的设计方法是以线性隔振理论为基础，即根据环评要求和地铁设计相关规范，设计具有满足规范要求和施工要求的浮置板轨道的固有频率及隔振器刚度，以经验为基础确定浮置板轨道的基本结构尺寸及隔振器的初步布置方式；在此基础上根据车辆轴重、轴距等信息对浮置板的结构及隔振器的刚度和布置方式进行校核。传统设计方法往往只针对系统的减振性能进行设计而未兼顾轮轨系统的动力学行为，更无法考虑轮轨系统的载荷特征，因此导致了浮置板轨道在实际使用中存在对低频隔振性能差和轮轨系统振动响应大等问题。本文基于非线性隔振理论，在对隔振器载荷特征分析的基础上，设计一种具有高静低动刚度特性的非线性隔振器，并对其阻尼特性进行优化，使其同时具有良好的低频隔振性能和振动位移控制能力，解决目前浮置板轨道系统存在的问题。

1 浮置板轨道隔振器载荷特征分析

1.1 车-线-隧系统动力学仿真模型的建立

建立车辆-轨道-隧道耦合动力学模型，是隔振器载荷特性分析及隔振器非线性特征设计和验证的基础。以某地铁线路的浮置板轨道为例，如图1所示，根据某B型地铁车辆及轨道和隧道的动力学参数建立车辆-浮置板轨道-隧道系统仿真分析模型，如图2所示。其中浮置板与隧道模型通过外部有限元模型导入，隧道壁通过弹簧阻尼单元与外部连接来模拟土层；模型中浮置板轨道系统由钢轨、扣件、轨道板及钢弹簧组成，其中钢轨采用铁木辛柯梁模拟，扣件采用弹簧阻尼单元进行模拟，钢弹簧采用非线性弹簧力元。轨道设置为：普通整体道床+5段25 m长浮置板道床+普通整体道床，建立浮置板轨道时既考虑了板与板之间起连接作用的剪力铰，又考虑浮置板间钢弹簧的局部加密情况，如图3所示。为了能够反映相邻车辆转向架对浮置板以及钢轨动态下沉量和扣件力的影响，本文采用三车模型进行仿真模拟。轮轨接触采用UM软件柔性轨道模块中自带的Kik-Piotrowski多点非赫兹接触模型来计算轮轨蠕滑力，该模型可以考虑车轮和钢轨的微小穿透，法向压力分布沿前进方向呈椭圆形状，切向接触斑形状为非椭圆。模型的仿真结果经过与实测数据进行对比修正后，取列车运行速度为80 km/h的隔振器支反力作为非线性系统的设计输入，非线性车-线系统根据计算得到的非线性隔振器设计参数对线性隔振器参数进行替换，非线性车-线系统模型的其他设置同线性系统。

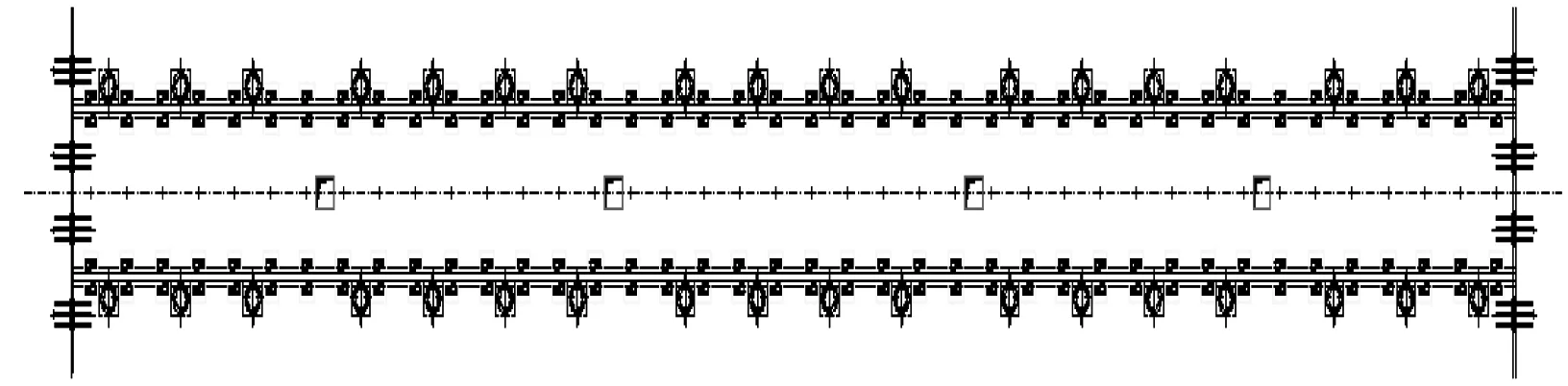
(a) 纵向布置图

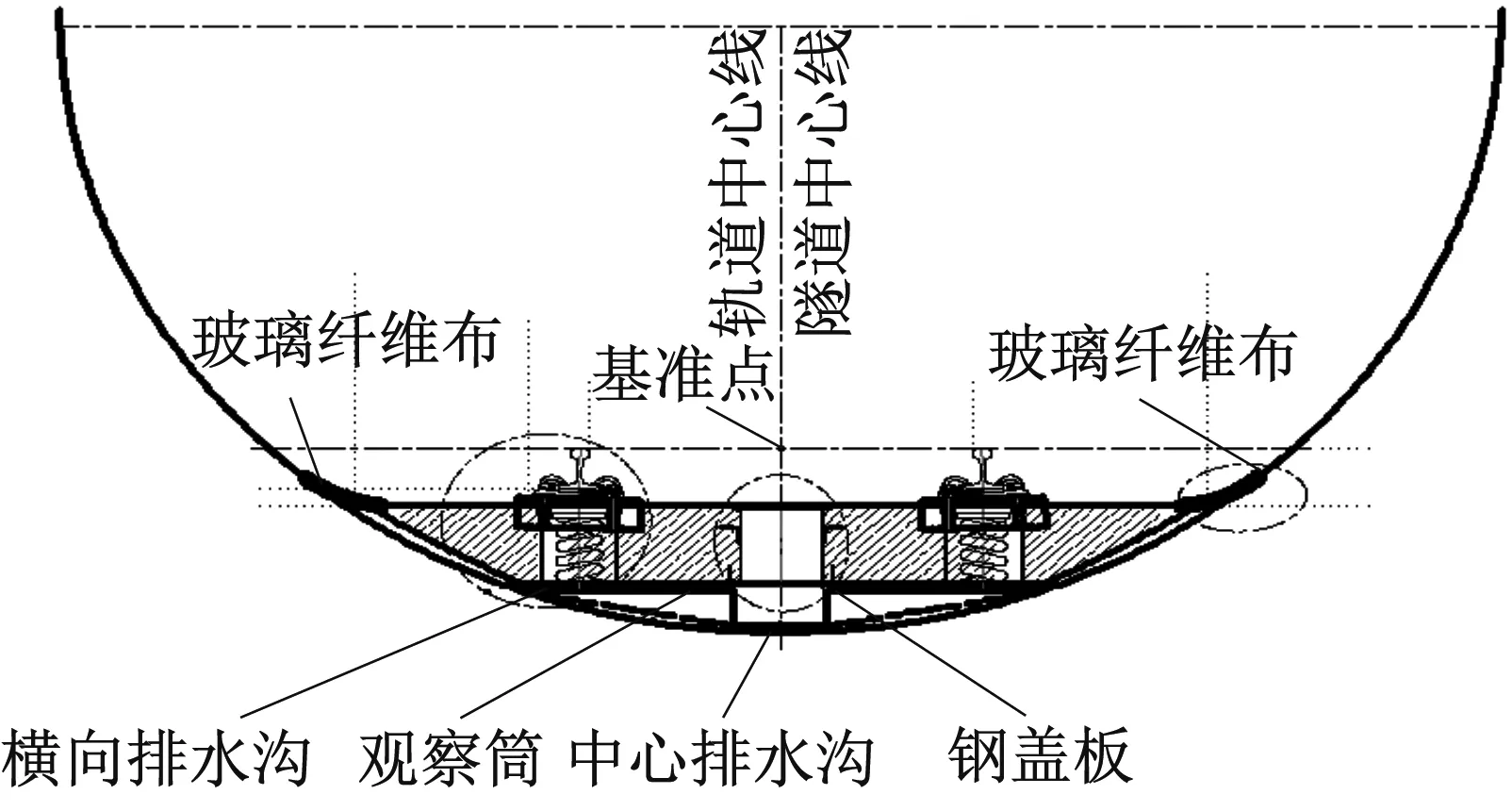
(b) 断面结构图

1.2 浮置板轨道隔振器载荷特征分析

准确获取并分析钢弹簧隔振器的载荷谱特点是非线性隔振器设计的基础，本节基于1.1节建立的车辆-轨道-隧道耦合动力学模型进行隔振器载荷谱的分析。中间板前端部、中部和后端部隔振器的垂向载荷时间历程，如图4所示。图4中隔振器受压力为负，受拉力为正，由图4可知，浮置板中部隔振器受力最大，这是由于浮置板中部板的柔性较大。因此在后续分析中，以受力最大的中部隔振器作为研究对象。对浮置板中部隔振器载荷曲线进行频谱分析，如图5所示。由图5可知，隔振器载荷分为准静态冲击荷载(4 Hz以下，移动质量引起的冲击荷载，以下简称冲击荷载)与动态荷载(4 Hz以上)，且冲击荷载要远大于动态荷载，冲击荷载主要影响浮置板位移，而动态荷载主要影响环境振动。

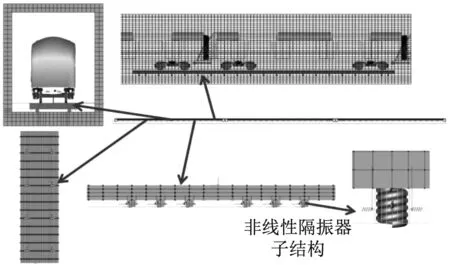
(a) 系统仿真模型

(b) 隧道模型

(b) 正视图

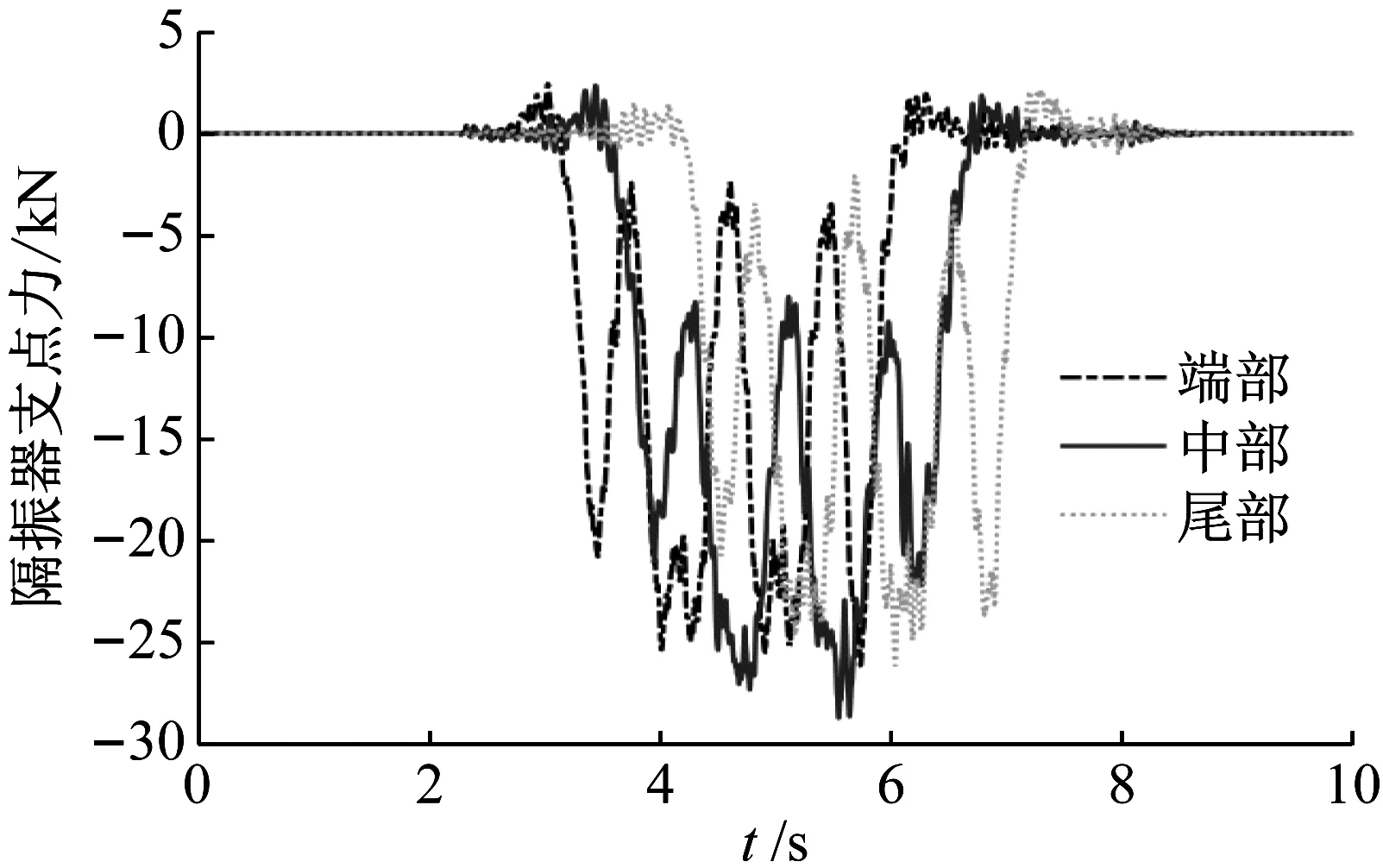
图4 隔振器垂向载荷

非线性浮置板轨道系统的设计需要同时考虑浮置板的位移控制与振动控制，因此，将隔振器载荷按照冲击载荷与动态载荷进行分解，使得非线性系统的设计目标更加明确，如图6所示。由6(a)、图6(c)可知，隔振器冲击载荷呈现4个峰(谷)值：P1为两节车相邻转向架引起的荷载最小值；P2为头尾转向架引起的荷载最小值；P3为头尾转向架作用于隔振器上的最大荷载；P4为两节车相邻转向架作用于隔振器上的最大荷载，如表2所示。表2中：AW0为空载工况；AW2为正常荷载工况；AW3为满载工况。由图6(d)可知，动态荷载的振动能量主要集中在10 Hz附近。

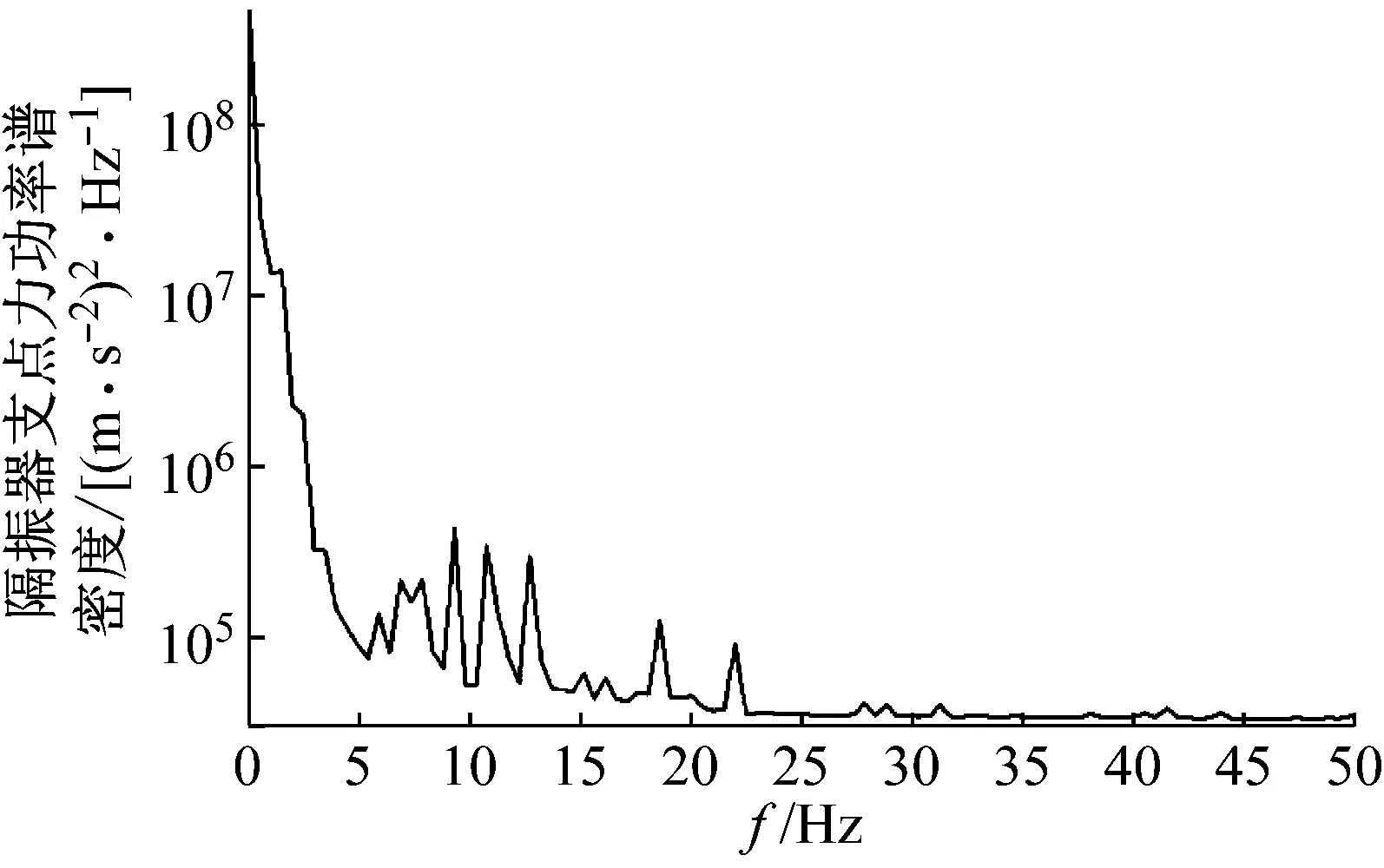
图5 浮置板中隔振器载荷功率谱密度图

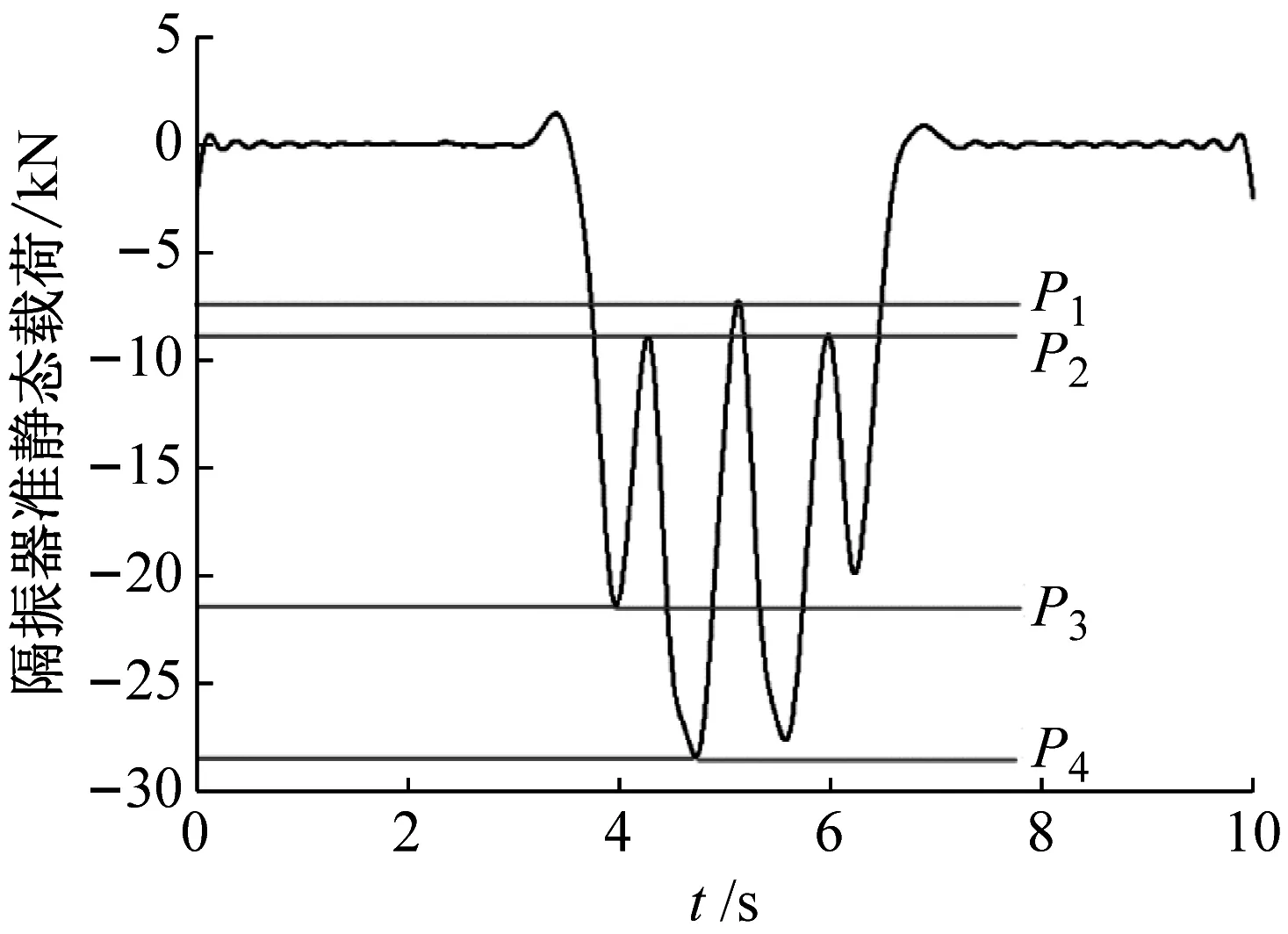
(a) 冲击载荷部分

(b) 动态载荷部分

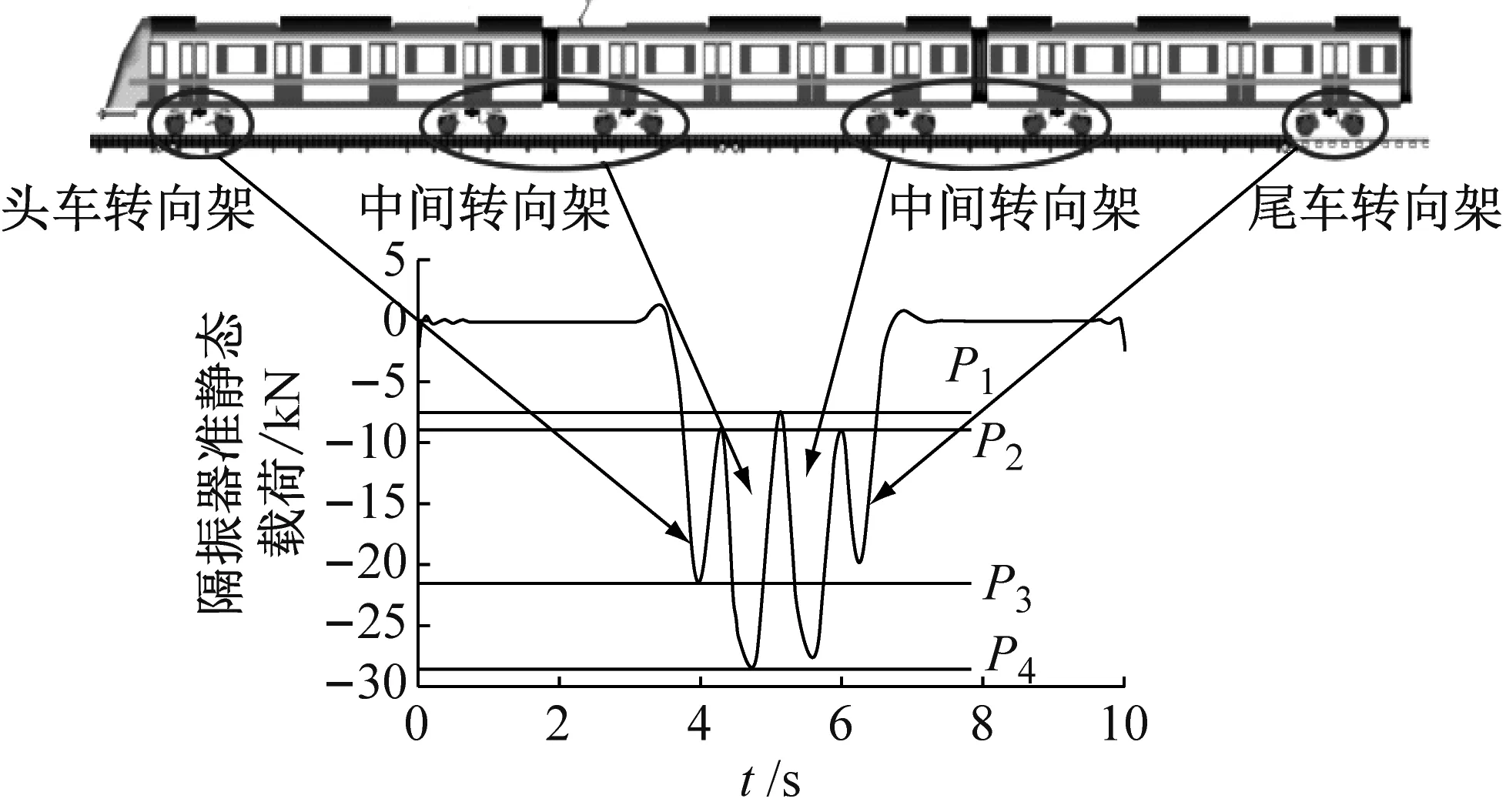
(c) 冲击载荷实际意义

(d) 动态载荷功率谱密度

准确提出非线性浮置板轨道系统的控制及优化目标是确定非线性浮置板轨道系统关键设计参数的关键，因此还需要结合列车经过浮置板轨道的动态过程对隔振器载荷的特征进行分析。列车经过浮置板轨道的全过程，如图7所示。由图7可知：在静平衡位置处(分别对应列车开始驶入浮置板前和刚驶出浮置板)的隔振器载荷的动态变化为隔振器未受到列车冲击载荷时的自由振动；当列车进入浮置板轨道时，在冲击载荷上叠加有动态的随机振动载荷。隔振器支反力在不同位置处的振动幅度曲线图，如图8所示。其中用灰度区分每一处响应所处在的由冲击成分引起的荷载发生位置，从中容易发现：绝大部分随机振动均产生在位置P0以及位置P3，P4附近，小部分发生在位置P1，P2附近，其他位置几乎没有随机振动成分；并且可以发现位置P1，P2与位置P0的位移差值均约为1.5 mm，若将位置P1，P2与位置P0分别进行力曲线优化，将对设备的加工精度、疲劳性能以及维护难度提出极高要求。因此从实际工程可行性角度考虑，只针对位置P0以及位置P3，P4附近存在的随机振动成分加以隔离，即保证系统在满足对冲击部分能量的储存能力的前提下，应在位置P0以及位置P3，P4附近具有尽可能小的刚度。

2 隔振器高静低动刚度曲线的设计

2.1 非线性刚度曲线设计目标

基于第1章隔振器载荷动态特征，定性判断所构造的非线性刚度曲线应保证系统在静平衡位置处(即车辆驶入浮置板前及车辆驶离浮置板后)和冲击载荷的极值位置处具有较好的隔振效果，同时抑制车辆驶入前和驶离后浮置板的自由振荡以及冲击动载荷引起的振荡。为保证系统具有足够的储能能力，使系统的大刚度区间尽可能发生在无明显振荡区域，且使系统最大刚度值在保证储能能力的前提下尽可能小。

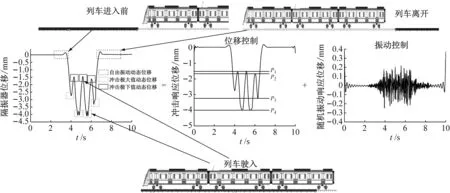
图7 基于隔振器载荷特征的振动控制目标

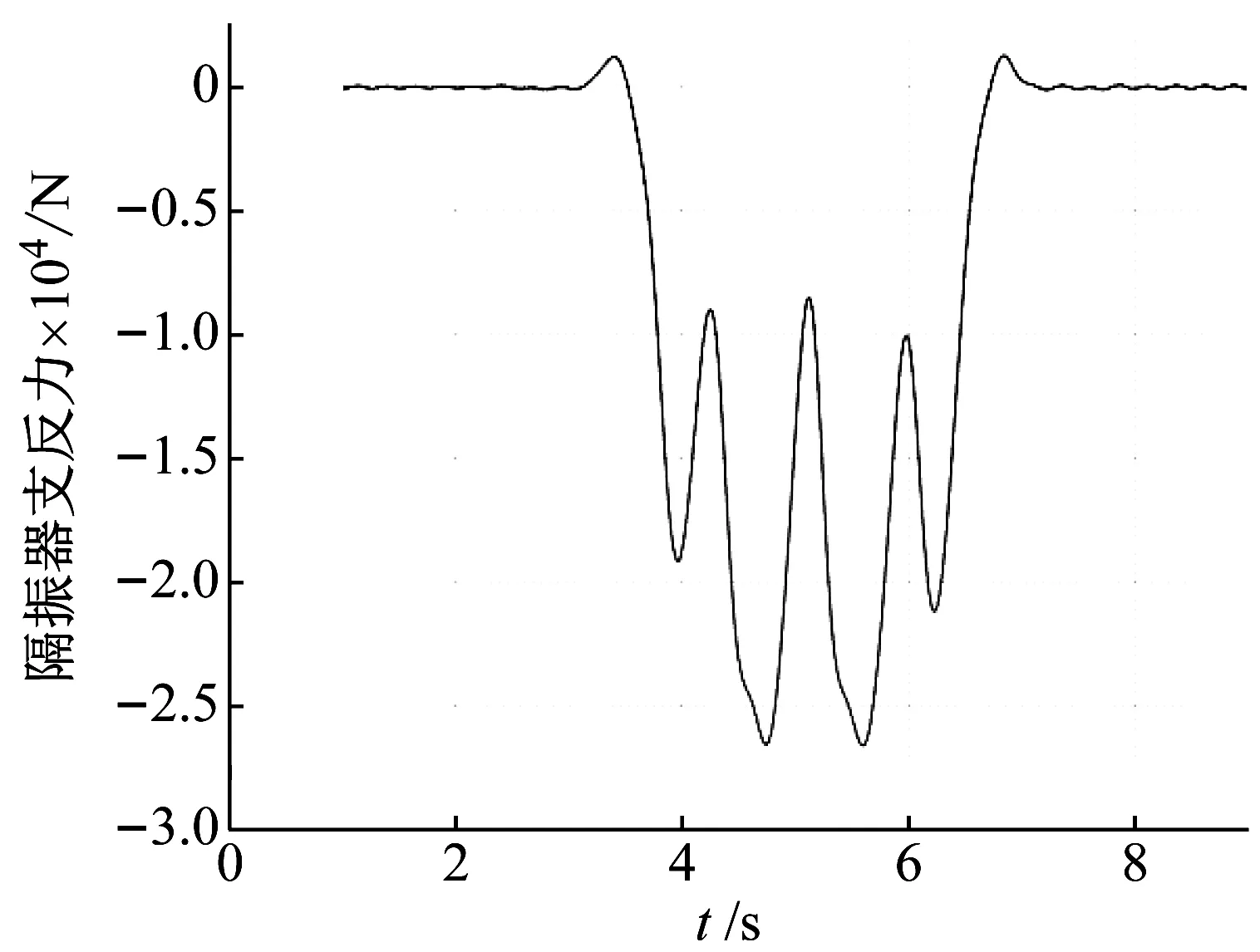
(a) 冲击响应部分

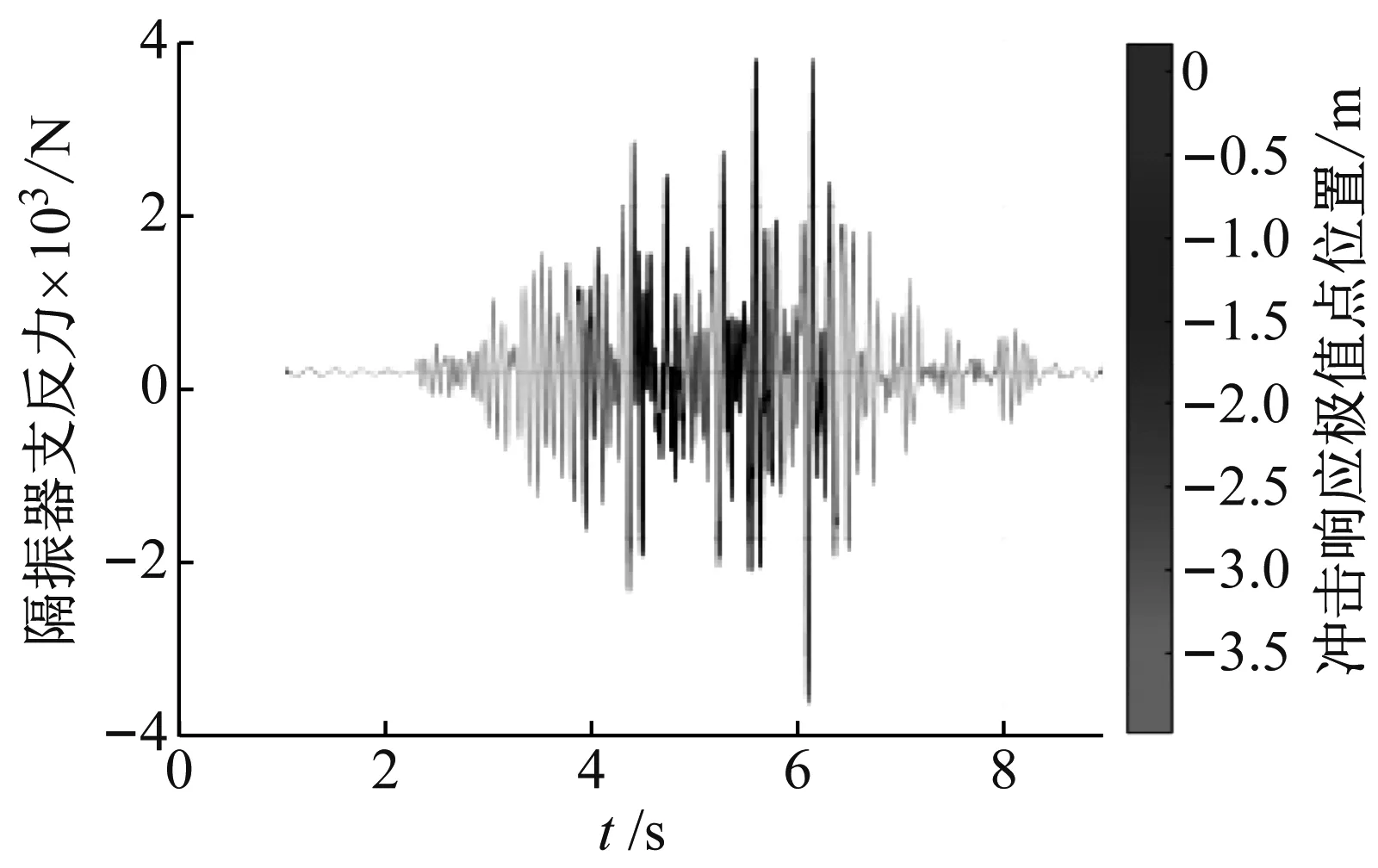
(b) 动态载荷响应部分

非线性隔振器刚度曲线设计原理示意图，如图9所示。图9中：虚线表示传统钢弹簧隔振器刚度曲线示意图；灰线表示非线性隔振器刚度曲线示意图。根据实际工程设计需求，分别按照起始隔振频率控制需求、振动位移控制需求和振动衰减速度控制需求三方面对非线性隔振曲线进行设计：① 尽可能降低浮置板轨道在振动平衡位置附近的刚度，降低系统的起始隔振频率，保证系统在浮置板一阶固有频率(10 Hz)附近具有最大的振动抑制能力；② 当系统位移响应超过设计值时迅速增大系统等效刚度，使系统在动态载荷作用下的位移响应过大时可以被迅速拉回至平衡点附近，以限制浮置板的动态位移；③ 提高浮置板轨道系统的振动衰减速度。另外，系统参数设计优化过程中要满足浮置板轨道隔振器的安装尺寸、加工制作等方面的要求。

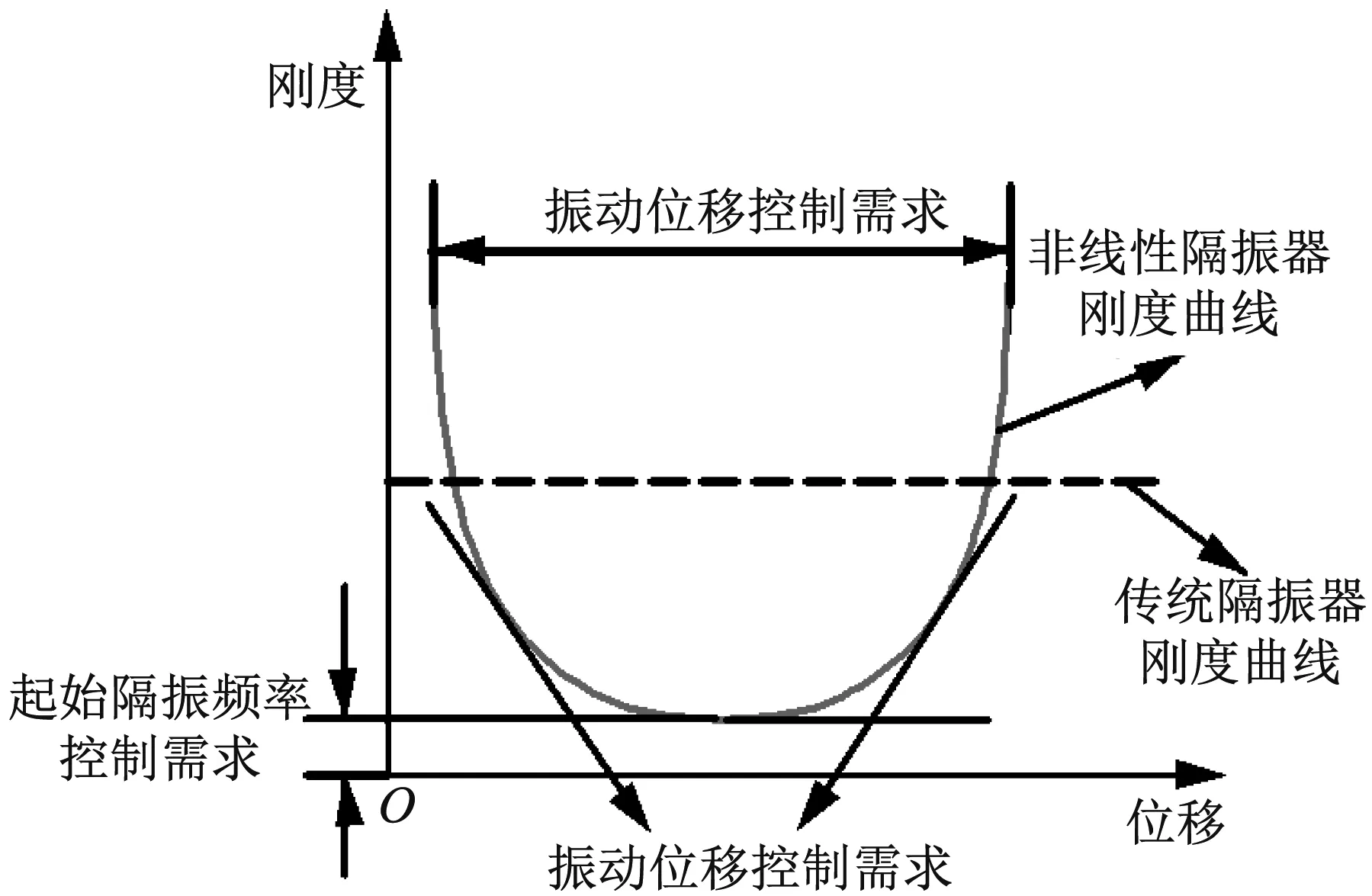
图9 非线性隔振器刚度曲线设计原理图

因此通过结合载荷分析结果，考虑设计一种非线性隔振器，旨在保证系统具有对浮置板足够的承载能力；以及在空载至准静态载荷之间具有足够的等效刚度抑制响应位移；同时保证系统在随机载荷集中的频率附近具有较高的隔振性能。

2.2 非线性动力学分析模型及静力学特性分析

本文基于SD(smooth-discontinue)振子几何非线性隔振理论，根据实际设计需求和目标构造非线性动力学方程，进而获得满足实际情况的最优设计参数。建立的单隔振器力学模型，如图10所示。图10中质量为m的振子在竖直方向振动，其通过承载弹簧和阻尼与基础相连，垂直弹簧为系统提供正向承载力。水平弹簧-连杆机构为系统提供负刚度，连杆一端与质量为m的振子铰接，另一端铰接于水平放置的弹簧，弹簧末端与基础相连。水平弹簧刚度为k1，竖向弹簧刚度为k，阻尼为c，非线性系统的初始平衡位移距离水平弹簧的高度为d，连杆长度为l，弹簧原长为L，水平弹簧原长末端到振子中心的水平距离为B。正常工作状态下，刚度为k的竖向弹簧处于预压缩状态来承载浮置板和列车的重力载荷，刚度为k1的水平弹簧处于预压缩状态保证弹簧-连杆机构为系统提供负刚度，使得正负刚度并联在振动范围内形成非线性刚度。

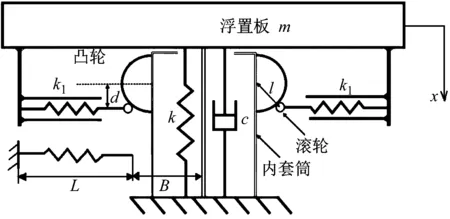
图10 浮置板非线性隔振器示意图

根据非线性隔振系统受力分析，得到系统在重力平衡下的运动方程

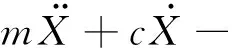
(1)

对式(1)所示的非线性隔振系统动力学方程进行无量纲化，得到

(2)

根据式(2)做出系统等效恢复力与刚度特性曲线，所用恢复力方程为

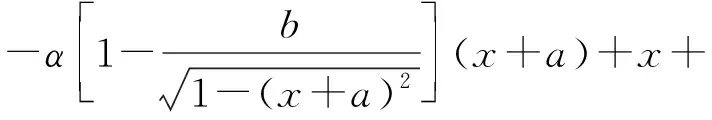
(3)

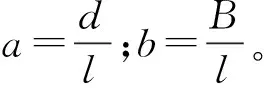
非线性系统等效刚度为

(4)

(a) 系统恢复力-位移曲线

(b) 系统刚度-位移曲线

(a) 系统的恢复力-位移曲线

(b) 系统的刚度-位移曲线

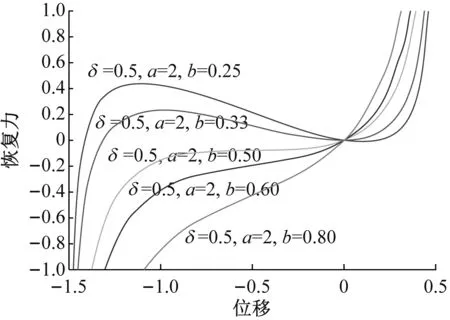
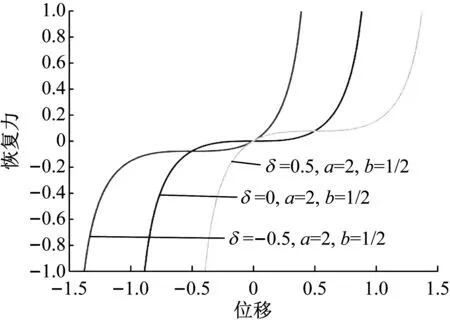
(a) b对系统恢复力-位移曲线的影响

(c) α对系统恢复力-位移曲线的影响

根据设计目标、非线性动力学方程及其参数影响，优化得到满足要求的非线性恢复力-位移和非线性刚度-位移曲线，如图14所示。由图14可知，在静平衡位置附近，相比线性系统，非线性系统具有较小的刚度，当系统位移超过设计值时非线性系统的等效刚度迅速增大，使系统在动态载荷作用下的位移响应过大时可以被迅速拉回至平衡点附近，以限制浮置板的动态位移。

2.3 非线性隔振系统动力学特性研究

本节主要研究具有2.2节设计出的非线性刚度曲线的单自由度隔振系统(见图10)的动力学特性，主要是谐波激励下的频率响应特性与力传递率特性。

根据图10所示的浮置板-非线性隔振器设计结构，得到非线性隔振系统的非保守受迫动系统的动力学方程

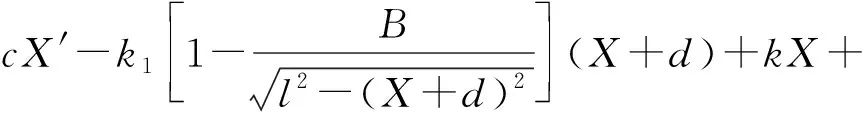
(5)

式中：F0为外激励直流项；F为周期外激励振幅；Ω为外激励频率；t为时间；φ为相位角。对该方程进行无量纲化处理，方程可表示为

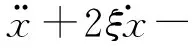
(6)

式中：f0为无量纲外激励直流项；f为无量纲周期外激励振幅；ω为无量纲外激励频率；τ为无量纲时间。

对式(6)应用谐波平衡法求解并进行化简可以得到系统的频率响应函数曲线和力传递率曲线分别如图15和图16所示。图15(a)、图15(b)以及图15(c)分别展示了由系统的非对称非线性特征所引发的无量纲振幅直流分量、一次谐波分量以及合振幅与外激励角频率之间的关系。可以发现，由于系统的非线性特征，系统共振峰相比线性系统发生左移，即系统隔振频率有所降低，均发生在约0.75倍固有频率附近。且当外激励频率越接近于共振频率时，直流分量以及一次谐波分量幅值分别趋近于最小值以及最大值。

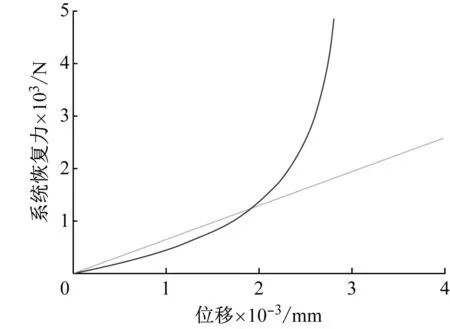
(a) 恢复力-位移曲线

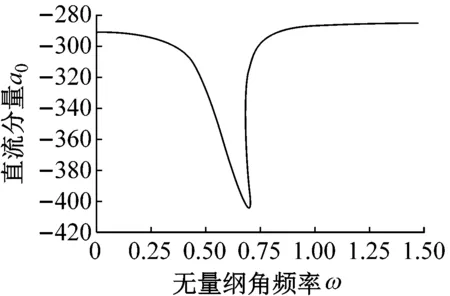
(a) 无量纲直流分量与角频率关系曲线

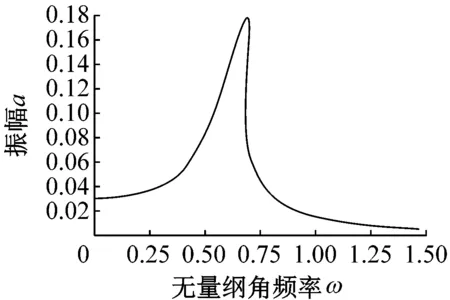
(b) 无量纲一次谐波幅值与角频率关系曲线

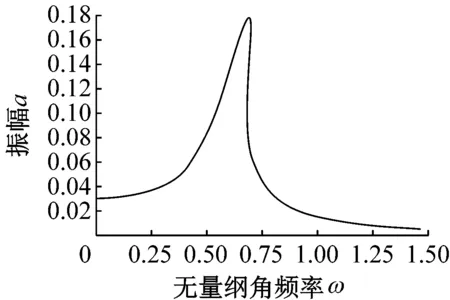
(c) 无量纲峰值响应与角频率关系曲线

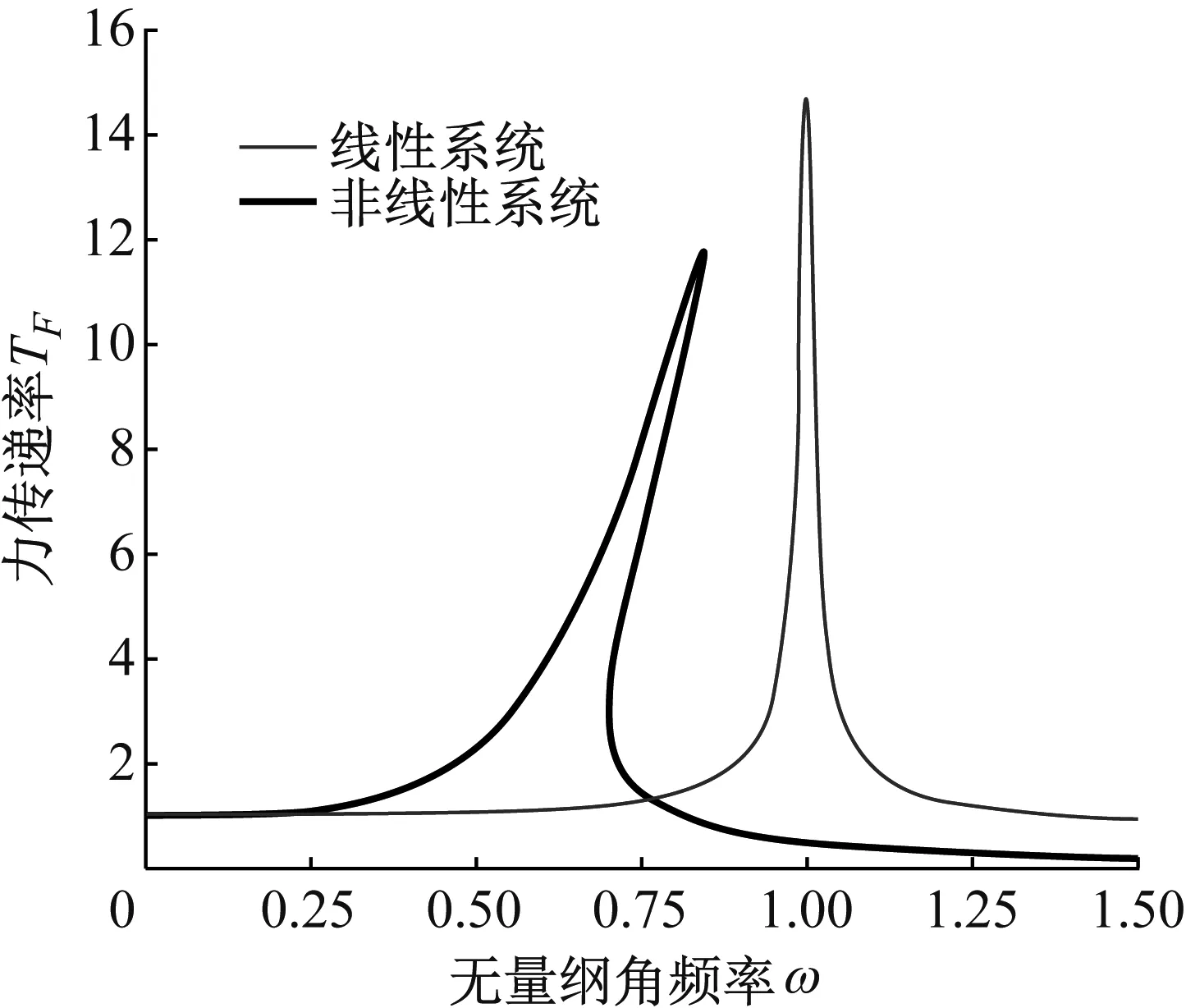
图16 隔振器力传递率曲线

为了分析系统的隔振性能，给出具有谐波激励作用下非线性动力系统的传递率定义式

(7)

式中：Fmax为载荷传递给基础的力的最大值；f为激励频率的动态分量。基于式(3)、式(4)、式(6)所述动力学方程，可以得到系统传递率曲线与线性系统传递率曲线的对比图，如图16所示。由图16可知，非线性系统相比线性系统具有更低的主共振频率，且共振峰值明显低于线性系统。

将非线性恢复力曲线代入图3所示的车辆-轨道-隧道耦合动力学模型，得到浮置板振动位移响应曲线图，如由17(a)所示。由图17(a)可知，非线性隔振系统相比原有线性系统的浮置板动态位移具有明显的抑制效果，最大位移减小约50%。非线性隔振系统在车辆运行时引起的隔振器支反力响应曲线及其频谱图，如图17(b)、图17(c)所示。由图17(b)、图17(c)可知，在浮置板一阶固有频率附近(5～15 Hz)具有十分明显的衰减效果，而在15 Hz以上与线性系统响应相比略有放大。从以上结果可知，渐硬系统相比线性系统具有如下优势：① 振动位移抑制效果明显；② 静平衡位置附近高频振荡抑制效果明显；③ 隔振器支反力响应在浮置板一阶频率附近(5～15 Hz)衰减效果明显。同时此类系统仍存在以下缺陷：系统达到最大动载附近后的高频振荡衰减效果不明显， 15 Hz以上略有放大。为了抑制振源处位移响应，导致渐硬系统在位移较大(未超出非线性区域)的情况下整体刚度远大于线性系统，而当位移响应超出非线性区域后系统刚度也仅与线性系统刚度相等，因而向基础传递的衰减能力会受到一定抑制，引起在最大动载荷处的振动衰减效果不明显，进而导致系统无法具有全频段的振动衰减效果。

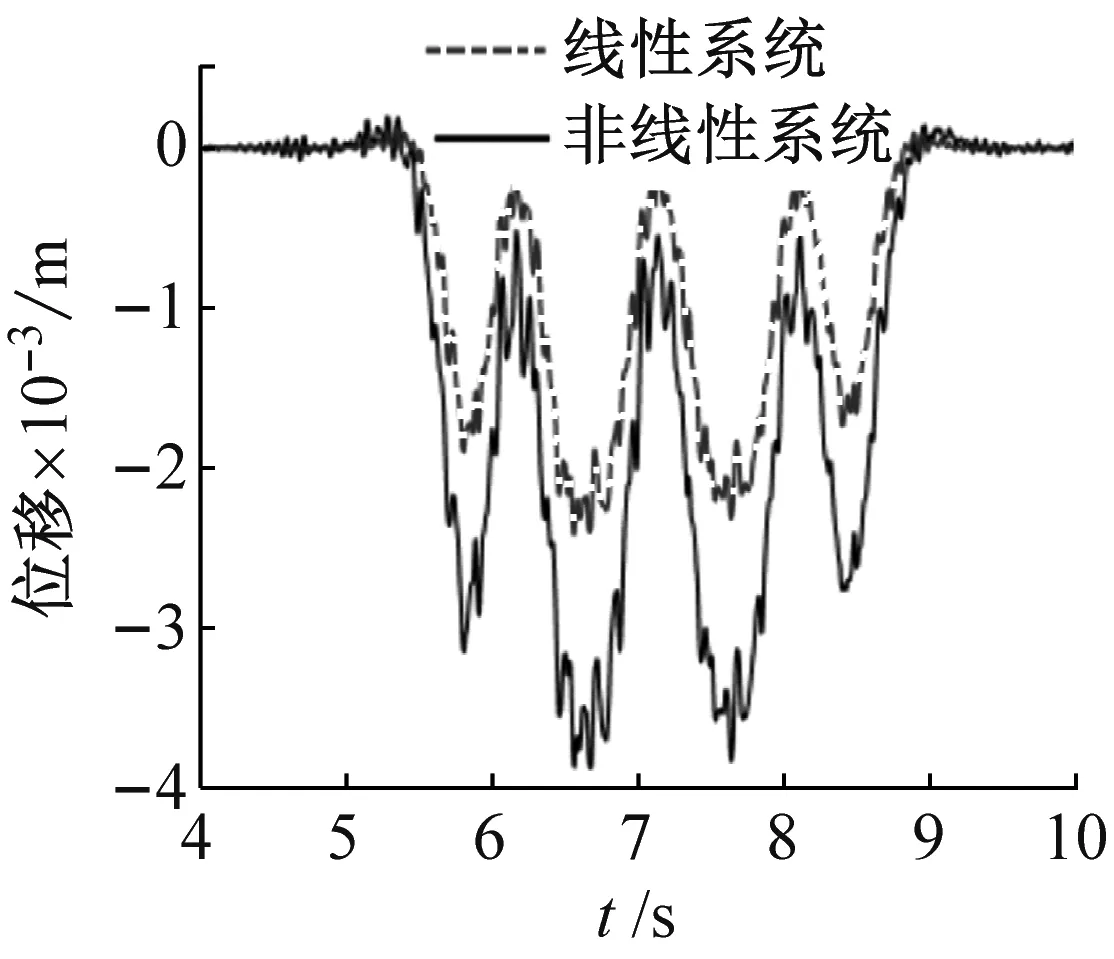
(a) 浮置板位移动态响应曲线图

3 非线性隔振器最优阻尼曲线优化设计

由第2章的分析可知，渐硬刚度曲线在位置P3，P4处存在振动放大现象，因此考虑增大系统在位置P3，P4处的阻尼以抑制系统由于刚度增大引起的振动放大现象。本章在隔振器高静低动刚度曲线的基础上，设计与之匹配的最优隔振器阻尼曲线，如图18所示。进一步提高其隔振性能。

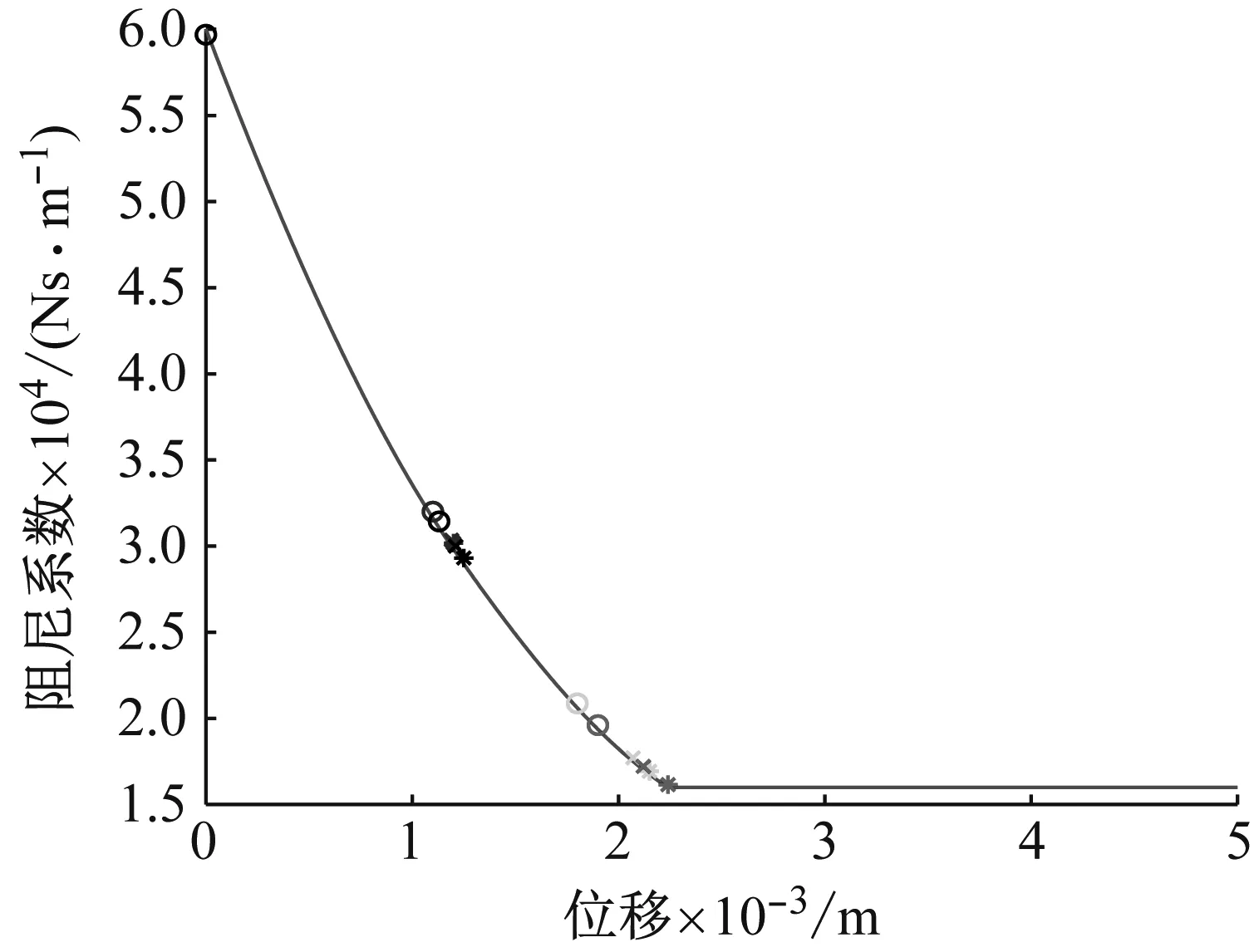
图18 非线性阻尼曲线

将该非线性阻尼曲线代入车辆轨道耦合动力学分析模型中进行优化计算，优化目标为降低隔振器支反力，其结果如图19所示。由图19(a)隔振器支反力动态部分时域曲线可知，在动态载荷较大的位置P3，P4处施加大阻尼可以极大程度抑制动态载荷峰值。由图19(b)～图19(d)可知，非线性阻尼对动态载荷的低频部分(≤20 Hz)有较明显的抑制效果；在中高频部分(>20 Hz)，非线性阻尼也有较好的振动控制效果。

4 非线性减振轨道系统仿真验证

将优化后得到的非线性刚度和非线性阻尼曲线代入图3所示的车辆-轨道-隧道系统动力学模型中，模拟列车运行工况下非线性轨道系统的隔振效果和轨道动态响应，计算得到浮置板振动加速度及隧道壁分频振级图，如图20所示。由图20(a)可知,非线性隔振器可以显著降低浮置板轨道的加速度响应，振动加速度有效值从1.04 m/s2降低到了0.56 m/s2，降低了46%；由图20(b)可知，非线性浮置板减振轨道系统在低频段(≤20 Hz)的隔振效果优于线性系统，尤其在10 Hz左右处的衰减效果最为明显，达到11.83 dB。

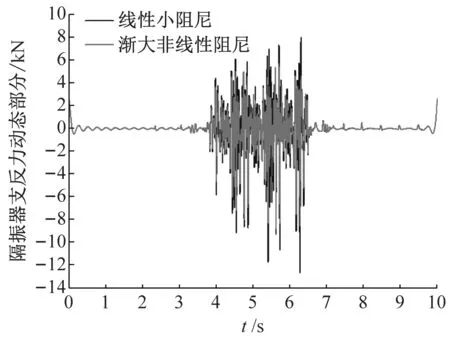
(a) 隔振器支反力动态部分

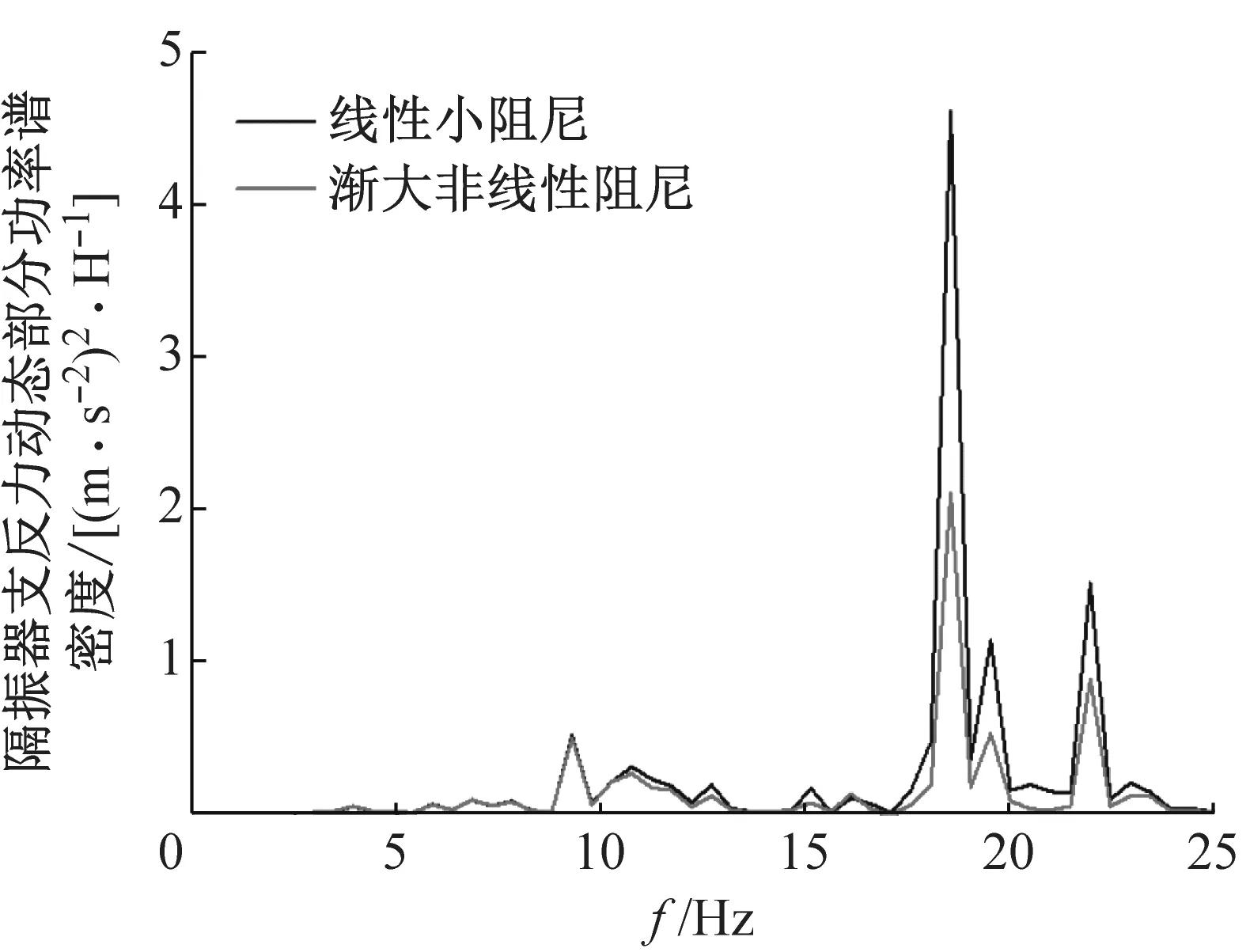
(c) 支反力低频部分功率谱密度放大图

(a) 浮置板加速度

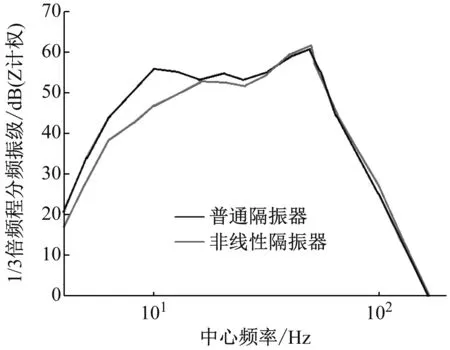
(b) 隧道壁分频振级

由于篇幅限制，本文只从理论上分析了浮置板高静低动非线性刚度隔振器设计理论及计算方法，目前已经生产出样品，并经过单隔振器实验和室内实验测试，相关内容将在后续文章中介绍。

5 结 论

本文在对隔振器载荷特征分析的基础上，提出了隔振器优化设计目标，基于非线性隔振理论，设计了具有高静低动刚度特性的非线性刚度曲线，并对其静态和动态特性进行了分析；针对所设计的非线性刚度曲线存在的缺陷，本文设计了与之匹配的最优隔振器阻尼曲线，进一步提高其隔振性能。最后，利用车辆-轨道-隧道耦合动力学评估模型进行仿真研究。通过研究本文得出以下结论：

(1) 非线性系统相比线性系统具有更低的主共振频率，且共振峰值明显低于线性系统。

(2) 相比既有线性系统，采用非线性隔振器的浮置板减振轨道系统可有效控制轨道板动态位移，轨道板动态位移可降低约50%。

(3) 相比既有线性系统，非线性浮置板减振轨道系统可显著降低轨道板的振动加速度响应，振动加速度有效值可降低约46%。

(4) 非线性浮置板减振轨道系统在低频段(≤20 Hz)的隔振效果优于线性系统，尤其在10 Hz左右处的衰减效果最为明显，达到 11.83 dB。