不同付费方式下医联体患者床位安排优化研究*

——李 娜 杜 涛 李金玉

近年来，随着医改的持续深入推进，医疗资源供给总量显著提升，但优质资源匮乏、分配不均等问题依旧存在，主要表现为二三级医院占有大量优质资源，导致大量患者涌入大医院，造成大医院拥堵问题严重。如何提高服务效率，是我国医院管理者思考并探索的问题。原国家卫生计生委《2015年卫生计生工作要点》(国卫办发〔2015〕3号)中提到，要以高血压、糖尿病等慢性病和结核病防治管理为突破口，探索按病种打包、上下联动等方法，构建基层首诊、双向转诊、急慢分治、上下联动的分级诊疗模式。《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要(草案)》也明确要求推行以按病种付费为主的多元复合式医保支付方式。在有限的病床资源条件下，针对不同类型(急诊、转诊择期、普通择期)患者，如何合理安排患者入院顺序及时间，以降低医院成本、提高医疗服务效率，是本研究亟待解决的问题。

1 文献回顾

首先，课题组以中国知网(CNKI)和SCI(SSCI)数据库为检索源，中文文献以“(医联体OR分级诊疗OR按病种付费)AND(医疗资源调度OR病床安排)”为检索式，英文文献以“bed allocation model OR hospital bed planning OR bed-occupancy management OR bed arrangement”为检索式，主要选取2011年1月1日-2021年11月30日发表在核心期刊的文献；同时，在确保较高相关度的基础上，选取部分经典文献作为参考。然后，将选取文献导入NoteExpress软件，由两名研究人员独立阅读标题和摘要，结合标准初步剔除与本研究相关性较小的文献。剔除标准：(1)述评类文献；(2)会议摘要，不提供全文。最后，由两名研究人员全文浏览保留文献，进行逐一筛选。纳入标准：与门诊、设备、病床等医疗资源相关文献。

通过对筛选文献进行阅读分析发现：(1)近年来，医疗资源调度优化已成为国内外学者研究的一大热点，其主要包括门诊预约调度优化、医疗设备调度优化、医生与病床调度优化和手术室资源调度优化等。如：楼昀等[1]围绕预约时间间隔、号源份额、预约渠道等进行优化，缩短了预约患者等候时间；梁峰等[2]基于马尔科夫决策(Markov Decision Process，MDP)模型和动态规划理论，得出了设备最优预约排程策略；刘强等[3]提出基于M/M/C模型来估计系统中患者等待时间，在此基础上研究并解决急诊医生排班问题；Ben Bachouch R等[4]将患者划分为急诊患者和择期患者，综合考虑病理之间不相容、护理连续性以及性别等因素，建立了病床安排线性整数规划模型，解决了医院病床安排问题；宋鸿芳等[5]将医疗服务分为两个阶段，研究探讨病床资源供需失衡问题；王珊珊等[6]在考虑手术室加班机会约束基础上，提出了手术计划随机模型；彭春等[7]考虑下游重症监护室容量，建立了鲁棒手术计划调度。(2)随着分级诊疗模式的顺利实施，国内学者开始探索医疗转诊和优质医疗资源再分配问题。如：孔颖文等[8]从双向转诊各相关利益方出发，寻找了分级诊疗中存在“下转难”现象的根源；莫钒等[9]基于马尔科夫理论建立了模型，研究了不同等级医院间合作最优转诊策略；徐芳等[10]探析了分级诊疗下各利益主体的态度，并剖析了分级诊疗政策实施受阻的背后诱因。(3)针对按项目付费制度诱导的过度用药、过度服务等问题，国内学者对疾病诊断相关分组(Diagnosis Related Groups，DRGs)也纷纷展开了研究，主要分为两类：基于DRGs的医疗服务绩效评价研究；各病种DRGs病例组合研究。如：罗玉英等[11]基于DRGs对比分析了同级民营医院与公立医院住院医疗服务的绩效差异；吴学智[12]利用决策树建立了急性阑尾炎患者的DRGs病例组合模型，探讨了急性阑尾炎不同病例组合住院费用标准。(4)国内外学者研究病床安排问题时多采用模型法，即运用运筹学相关理论和方法解决现实问题。如：Gorunescu F等[13]利用经典排队理论研究了医院科室病床安排问题，并提出了M/Ph/C优化排队模型；Li X等[14]以每日医院收益最大化为目标，在建立M/Ph/C排队模型基础上，运用目标规划方法进行求解，解决了医院病床资源浪费问题；Gorunescu M等[15]利用M/ph/C排队模型已有结论，提出了一种优化病床数量的方法，以使延迟概率保持在可接受水平；邹长福等[16]根据患者优先级建立动态控制排队模型，并通过层次分析法和熵值法建立的病床安排和理性评价模型对其进行检验，得出在现有医疗体制下动态控制排队模型优于先来先服务(First Come First Service，FCFS)模型；李珍萍等[17]以患者平均等待时间最短为目标，建立了病床安排问题的线性规划模型；费绍金[18]通过系统模拟方法，对比并讨论了各种入院和手术方案，建立了以平均逗留时间最短为目标的病床分配模型。

综上，大部分学者侧重于分级诊疗实施中不同医院之间的博弈、使用DRGs付费时各病种的病例组合费用、病床安排模型构建等单层面研究，未将分级诊疗和按DRGs付费与患者病床安排问题相结合。因此，本研究将患者分为急诊患者、转诊择期患者、普通择期患者，研究不同付费方式下医院如何安排患者的入院顺序及时间。

2 问题描述与数学建模

2.1 问题描述

患者来到一家三甲医院，医生会根据其患病情况作出是否需要入院治疗的判断。急诊患者只要有空闲病床需立刻安排入院；转诊择期患者可能存在等待病床情况，但由于医联体“绿色通道”，其等待时间相比普通择期患者短；普通择期患者可先在预约队列中等待，由系统确定具体入院时间。

本研究主要探讨确定环境下的患者病床安排问题。首先，假设已知每位患者的类型、病情、已等待时间以及未来一周每天将会出院的患者数量；然后，在此基础上，以收益最大化为目标，寻找未来一周的最优患者病床安排方案。

2.2 不同付费方式下医联体患者病床安排优化模型

由于不同层级医院医疗资源配置存在“马太效应”[19]，因此大医院常床位紧缺，导致大部分患者无法在登记后当周立刻入院。同时，大医院一般能够根据康复期患者身体情况提前预知下周每天将空出的病床数，故假设本周空床数为零且存在等待入院患者。此外，计划周期为7 d，且每周周日计划本周等待患者下一周入院顺序及时间。

考虑到医院是病床安排决策者，且公立医院具有一定公益性，故本研究站在医院管理者角度，将患者等待成本纳入医院支出部分，建立不同付费方式下医联体患者病床安排优化模型。医院收入主要来源于向患者提供医疗服务，医院支出包括医疗服务供给过程中医疗资源消耗和患者等待成本，因此本研究采用收益最大化作为目标函数。不同付费方式下医联体患者病床安排模型如下：

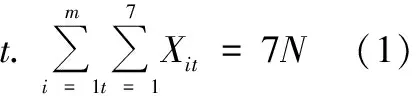
Xit,Bi{0,1}，RiD，CiR,Pi，diN+i=1,2…，m;t=1,2,…7 (3)

式中：Xit(i=1,2…，m;t=1,2,…7)为0～1变量，其中，Xit=1表示患者i在第td入院，Xit=0表示患者i不在第td入院；Bi(i=1,2,…,m)为0～1变量，其中，Bi=1表示患者i采用按DRGs付费，Bi=0表示患者i采用按项目付费；RiD表示患者采用按DRGs付费时，医院为患者i提供医疗服务所获得收入；Ci表示医院为患者i提供医疗服务所需要花费的成本；RiN表示患者按项目付费时，医院为患者i提供医疗服务所获得的收入；Pi表示患者i每多等待一天病情加重的单位成本；di表示患者i到本周日为止已等待的天数；Wi表示患者i从本周日到实际入院需等待的天数；T表示给定的计划周期长度(如1w)，tT;N表示每天出院人数，即每天空出的病床数。

目标函数第一部分是医院为采用按DRGs付费的患者提供医疗服务所获得的收入；第二部分是医院为采用按项目付费的患者提供医疗服务所获得的收入；第三部分是患者的等待成本，等待成本在一定程度上区分了不同类型患者的安排次序。其中：约束条件(1)表示下一周内病床每天都处于满负荷状态；约束条件(2)表示每位患者在下一周最多只能安排一次住院；约束条件(3)为决策变量取值约束。

本研究建立的模型为整数规划模型，而分支定界法是求解整数规划的一种常用方法[20]，故本研究采用此算法求解模型。其核心思想是对有约束条件的最优化问题的所有可行解空间进行搜索，具体算法流程为：

(IP)MaxcTx

&.t.Ax≤b,x{0,1}n

步骤一(初始)：求解原问题(IP)相应的线性规划问题，判断所得的解是否为整数解，若为整数解，则求解过程停止，否则将其目标函数值记为上界。

步骤二(分支)：用增加约束条件方法，把原问题分为两枝，并求解。

步骤三(定界)：根据步骤二，修改原问题的最优目标函数的上界和下界。

步骤四(比较与剪枝)：各分支的最优目标函数中若有小于下界者，则剪掉该分支，若大于上界，则重复步骤二和步骤三，直至最优目标函数值的上界等于下界时为止。

3 案例求解与分析

本研究以延安市医联体内某三甲医院产科病房病床为例。该病房共有110张病床，主要收治病种包括妊娠、人工流产、妇科肿瘤、月经不调等。由于妊娠这一病种的上转率明显优于其他病种且该病种DRGs实施效果较好，因此本研究重点探讨该病种患者的病床安排问题。

假设入院前等待时间对各类患者影响程度不同，如表1所示。急诊患者每多等待1 d对其疾病的影响程度高于其他两类患者，因此其单位等待成本最高；由于医联体内双向转诊中上转居多且患者病情严重需及时转向大医院就诊，因此转诊择期患者的单位等待成本紧随急诊患者之后，且高于普通择期患者。

表1 各类患者的单位等待成本

已知下一周等待入院患者共有20人且每天都会有3位患者出院，等待入院患者中有两位急诊患者(患者19、患者20)、一位转诊择期患者(患者6)，其余为普通择期患者。在阅读文献[21]基础上，患者已等待时间按照患者到达先后顺序依次赋值5、4、3、2、1。20位等待入院患者基本信息如表2所示。

3.1 按项目付费时患者入院顺序及时间分析

为便于分析，假设该院为本周20位等待入院患者提供医疗服务所获得的收入及成本与上周出院患者基本一致，且这20位患者均采用按项目付费方式。根据上周出院患者实际数据，按项目付费时该院提供医疗服务所获得收入及成本的变化趋势如图1所示：在按项目付费情况下，医院为每位患者提供医疗服务收入总是大于服务成本，并且收入和成本变化趋势基本相同。

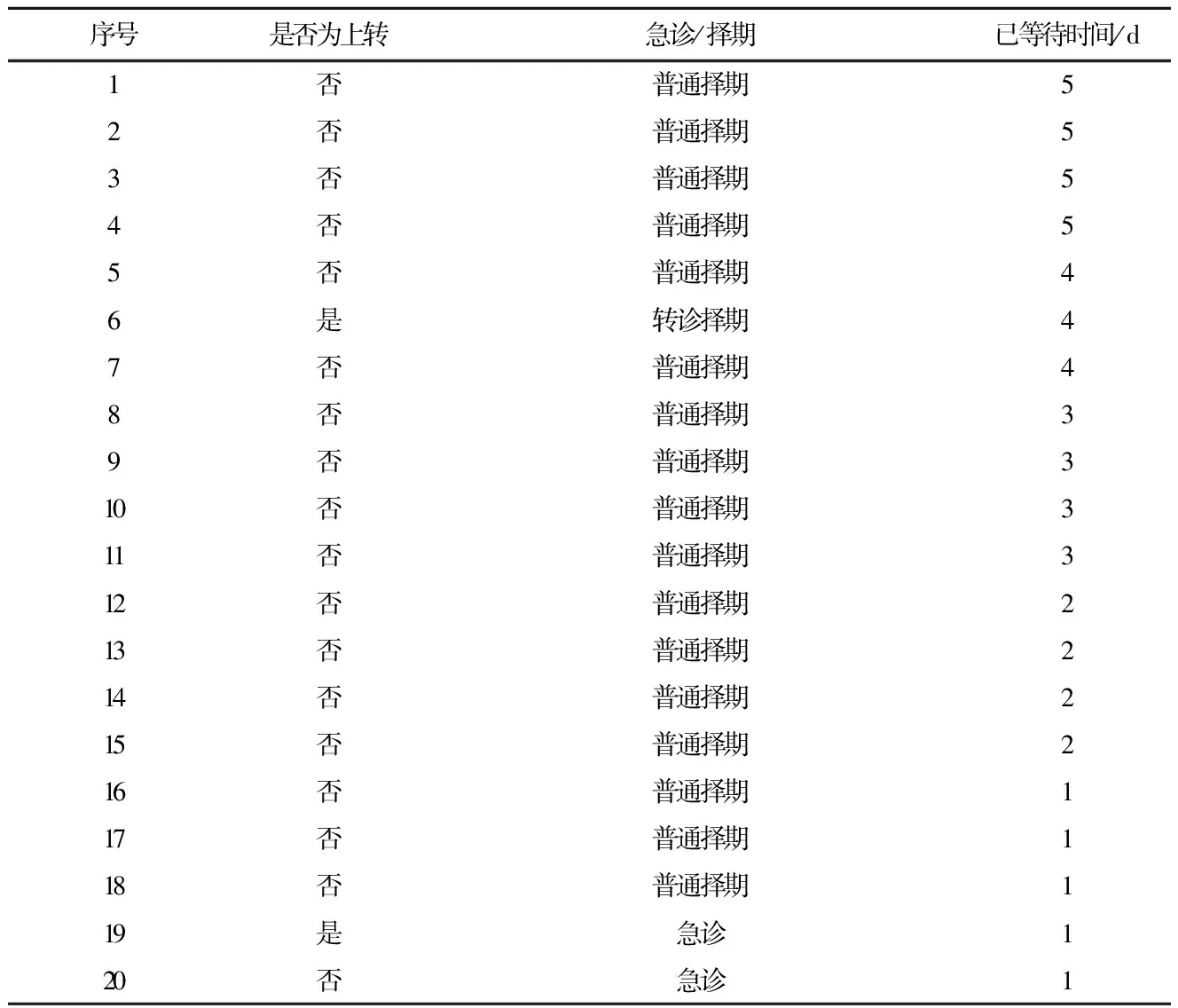
表2 20位等待入院患者基本信息

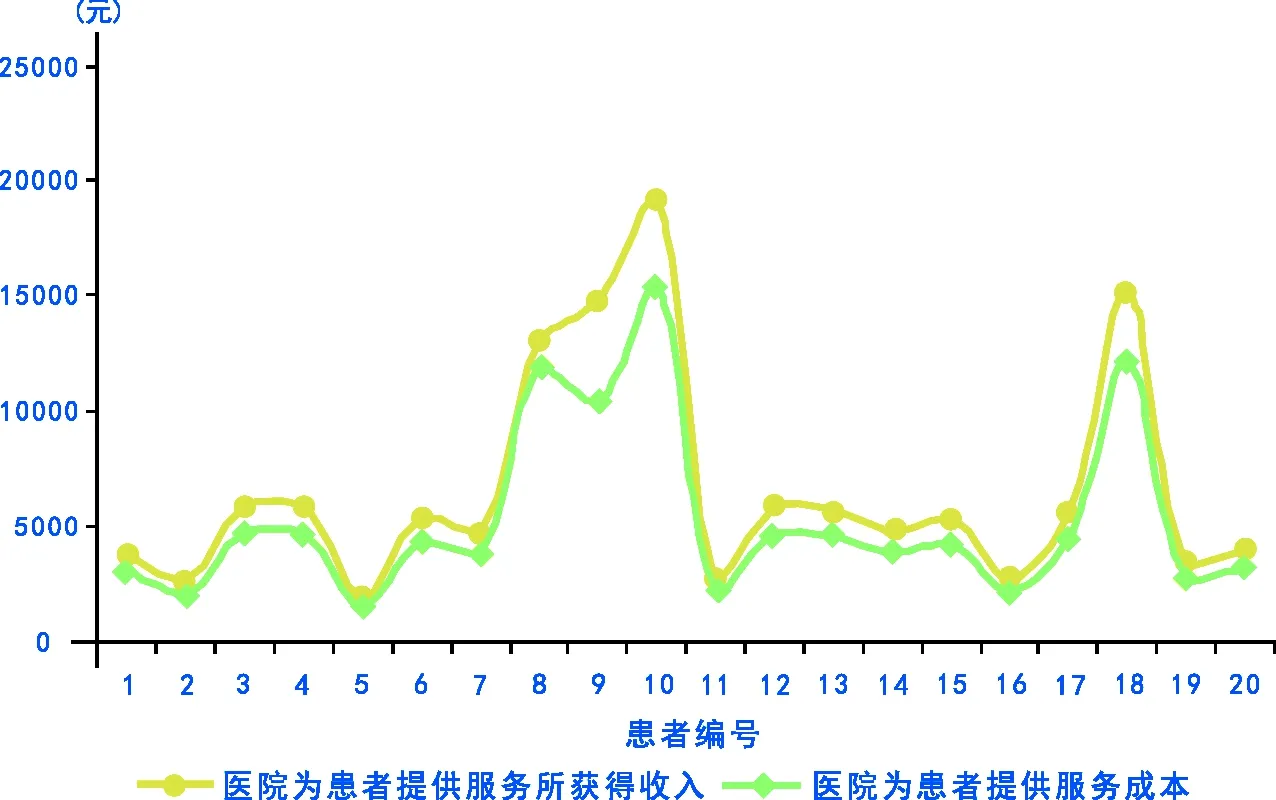
图1 按项目付费时医院为20位患者提供服务收入及成本趋势

假如按照FCFS原则安排患者入院顺序，经计算可得，该院未来一周收益为4 529元。将按项目付费时的实际数据代入模型，利用Lingo编写算法，可得出20位等待入院患者入院顺序及时间(表3)，经计算可得，该院未来一周收益为13 129.41元。

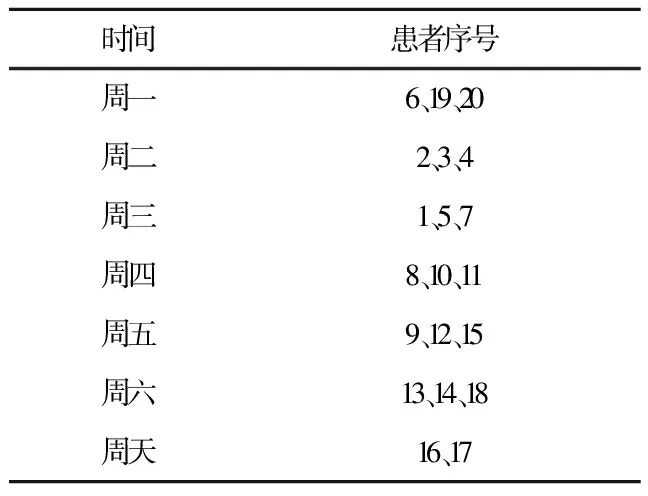
表3 按项目付费时未来一周每天入院患者序号

首先，从医院收益来看，按项目付费时，医院使用整数规划模型所获得的收益要高于按照FCFS原则进行安排的收益，并且整数规划模型能让医院的收益提高189.9%。其次，从一周患者总体健康效益来看，按照FCFS原则安排患者入院看似公平，但有可能耽误急重症患者最佳诊疗时机，造成患者健康效益低下。整数规划模型分析结果显示，急诊患者、转诊择期患者病床安排优先于普通择期患者，可有效规避重大疾病诊疗延误风险，提高患者平均健康水平。

3.2 按DRGs付费时患者入院顺序及时间分析

基于延安市DRGs实施背景，在阅读文献基础上，结合延安市医联体内某三甲医院实际收费数据，假设妊娠患者DRGs各分组住院费用标准如表4所示。

假设本周20位等待入院患者均采用按DRGs付费方式。基于患者实际，结合表4，可得出其在使用DRGs的情况下医院收入及成本趋势，如图2所示：按DRGs付费时，医院为患者提供医疗服务所获得收入可能会小于服务成本。

将数据代入模型，并通过Lingo算法计算出20位患者在按DRGs付费时未来一周入院顺序及时间，如表5所示。结果表明，在按DRGs付费时使用整数规划模型，医院获得最大收益为7 334元。

同理可得，按DRGs付费时，运用整数规划模型安排患者入院，医院所获得收益仍高于按FCFS原则安排患者入院所获得收益。通过计算可得，整数规划模型可以使医院收益增加61.9%。由表5可知，整数规划模型按DRGs付费时病床安排规则亦是急诊患者、转诊择期患者优先于普通择期患者。

表4 妊娠患者DRGs各分组住院费用标准

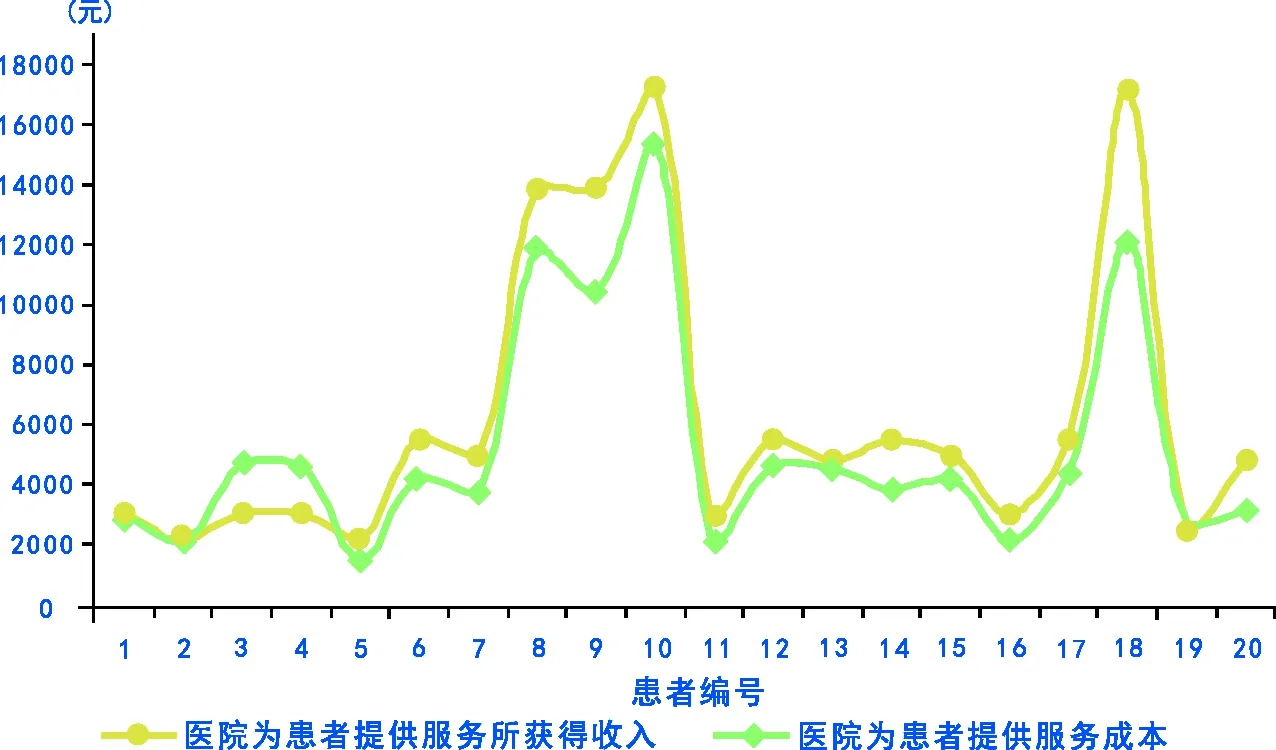
图2 按DRGs付费时医院为20位患者提供服务的成本及收入趋势

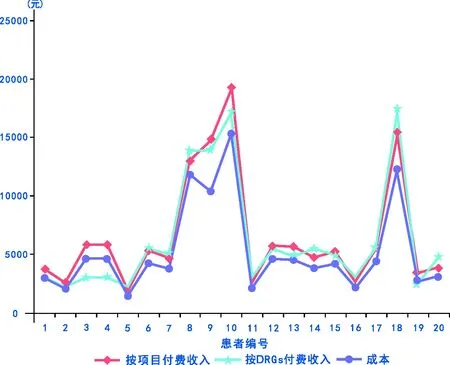
图3 不同付费方式下医院为20位患者提供医疗服务的成本和收入对比

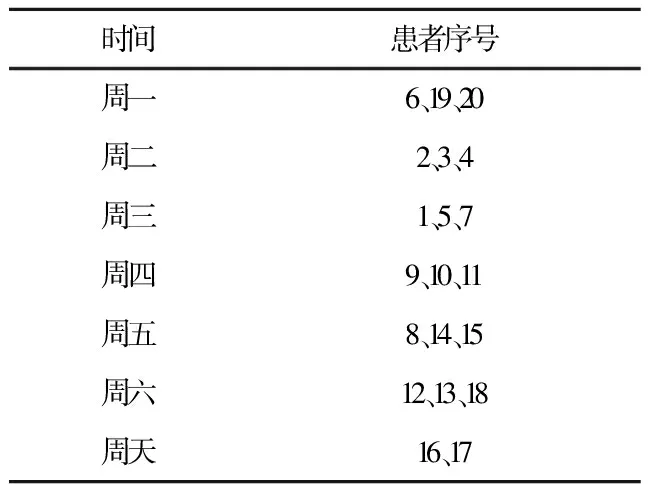
表5 按DRGs付费时未来一周每天入院患者序号

3.3 不同付费方式下患者入院顺序及时间对比分析

通过对比不同付费方式下患者的入院顺序及时间发现，患者无论采用哪种付费方式，整数规划模型所得的患者病床安排规则都优先考虑急诊患者、转诊择期患者，其次考虑普通择期患者，这在一定程度上提高了医院收益，同时也保障了患者总体健康效益。

在上述规则基础上，从同类型患者入院顺序及时间角度出发，进一步对比分析医院提供医疗服务的成本与收入，并绘制不同付费方式下该院为20位患者提供医疗服务的成本和收入对比图，如图3所示：患者8、患者9和患者12、患者14在按项目付费时的收入波动与其按DRGs付费时的收入波动不同。

对比表3和表5可得，按DRGs付费时，患者8和患者9、患者12和患者14入院顺序及时间与按项目付费时的入院顺序及时间不同。结合表2可见，患者8、患者9、患者12、患者14都是普通择期患者；并且患者8和患者9的患病类型、并发症状况、住院天数、等待天数都相同，但医院为不同患者提供的医疗服务成本存在差异，患者8、患者9的医疗服务成本分别为11 813.24元、10 417.42元。患者12和患者14同样除了医院为其提供医疗服务的成本不同以外，其他条件均相同，分别为4 629.05元、3 853.86元。为厘清医院提供医疗服务过程中的消耗与所获报酬之间的关系，引入财务管理中的成本费用净利率指标，其计算公式为：成本费用净利率=净利润÷成本费用总额×100%。通过计算可得，该院为患者8、患者9提供医疗服务时成本费用净利率分别为9%、24%，这说明患者8每消耗100元可以得到9元的净利润，而患者9每消耗100元能得到24元的利润。同理可得，该院为患者12提供医疗服务时成本费用净利率约为10%，为患者14提供医疗服务时成本费用净利率约为33%。由此可得，按DRGs付费时，整数规划模型对同类型、同病种、同症状的患者病床安排规则为成本较小的患者优先安排入院，这正好符合DRGs的推行目的。DRGs的使用可让医院在提供相应医疗服务之前预知此次医疗资源消耗上限，且以此作为盈亏线调动医院积极性[22]，这也证明该模型可在一定程度上提高医疗资源使用效率。

4 结论

本研究综合考虑付费方式和入院等待时间两个因素，研究了不同付费方式下医联体患者病床安排问题。本研究结果提示：首先，相对于FCFS原则，整数规划病床安排优化模型能在一定程度上提高医院收益；其次，整数规划模型在安排不同类型患者入院时，急诊患者和转诊择期患者优先于普通择期患者，这一规则未随付费方式变化而改变，说明该模型具有一定稳定性，同时也在一定程度上弥补了按FCFS原则安排患者入院的缺陷，保障了患者健康效益，体现了公立医院的公益性；再次，整数规划模型在安排按DRGs付费的同类型、同病种、同症状的患者入院时，成本较小患者优先安排入院，使得医院收益减少，而DRGs的实施就是在一定程度上利用医院收益的下降倒逼其提高资源使用效率，这说明该模型与DRGs政策实施目的相契合，也进一步证明了该模型的合理性。

但该模型也存在一定局限：(1)模型建立在医院某周已无空床且存在等待患者条件下，对于复杂情况需进一步验证；(2)模型使用前需对本周无法安排入院的等待患者的住院费用及分组进行初步预测。对此，建议在使用该模型时结合人工智能技术，以共同确定最终病床安排方案。