从一道抛物线开放题的多向探究谈探究教学

◎曹 一

(上海市育才中学，上海 201801)

在数学学科教学与学习中，发现和提出问题能有效地激活课堂，培养学生的创造性思维，促进学生对新问题进行有效而且积极的探究，传统数学教学注重训练学生的解题能力，而学生善于准确、高效地解决教材和教辅中呈现的问题，善于“学答”而不善于“学问”，从而忽视了培养学生发现问题、提出问题的能力，忽视了培养学生的批判性思维、创新性思维

一、原始问题

已知直线=-2与抛物线:=2相交于，两点,为坐标原点求证：⊥

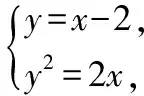
整理得：-2-4=0，∴+=2，=-4，

∴=(+2)(+2)=+2(+)+4=4，

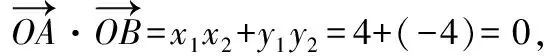
二、问题提出

上述习题由直线、抛物线、原点、垂直等基本要件构成，如何能改变相关要件提出新的命题呢？首先，将上述命题推广，使其成为特例，并做出解答；进一步适当改变或变换题目条件，提出问题，并进行多向探究本文先进行一般性探究，再从逆向、纵向、横向探究，以上探究都能得到满意的结论

(一)一般性探究

1已知直线=(-2)与抛物线:=2相交于、两点求证：⊥

=1，即上述原始问题

设(,),(,),

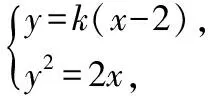
得：-2-4=0，∴=-4

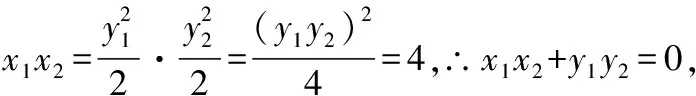
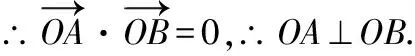
2已知直线=(-2)与抛物线:=2相交于，两点求证：⊥

=1，=1，即上述原始问题

设(,),(,),

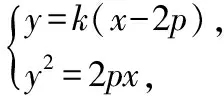
得：-2-4=0,∴=-4

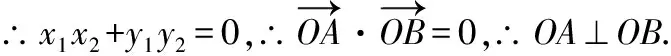
通过上述研究，其中发生变化的量是斜率，定点(2,0),⊥没有发生变化，本题中体现了变与不变的相对性及辩证性，⊥与无关，与定点(2,0)相关这里看似仍停留在传统教学层面，但解题思维要灵活得多，要素分析得透彻，为后续深层挖掘做准备

(二)逆向探究

3已知,在抛物线:=2(>0)上，且⊥求证：直线经过定点

设直线方程=(-)

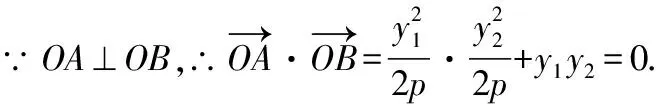
∴=-4

得：-2-2=0,∴=-2

∴=-4=-2,∴=2

∴直线过定点(2,0)

4已知、在抛物线:=2(>0)上，点(,)是抛物线上一定点，且⊥求证：直线经过定点

∵⊥，∴=-1，

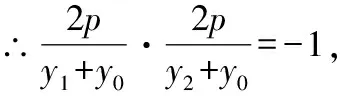
设直线:=(-)代入=2,

得:-2-2=0，

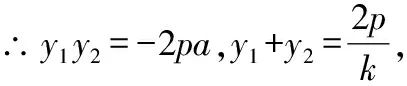
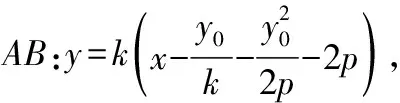
所以，过定点(+2,-)

直线的方程为：

⟹-(+)+2=0 (2)

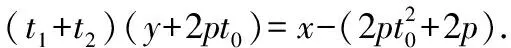
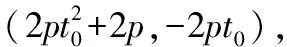
即定点(+2,-)

5已知，在抛物线:=2(>0)上，(,)是抛物线上一定点，·=，求证：直线经过定点

上题中斜率乘积等于-1改为即可得证

∵⊥,∴·=

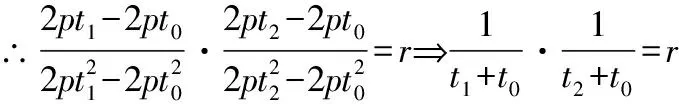
⟹-(+)+2=0 (2)

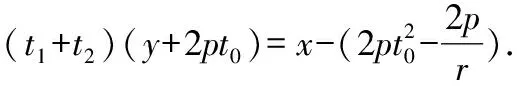
这里不仅有逆向思维，显示了证法的多样性，更将结论由特殊问题解决转向一般问题解决促成思维的功能性发展，使提出问题的层面上升了一个台阶

(三)纵向探究

6已知，在抛物线:=2(>0)上，且⊥，⊥，垂足为求点的轨迹方程，并说明它表示什么曲线

由变式3可知，直线经过定点(2,0)，又⊥,∴点的轨迹是以为直径的圆(除去原点)，其方程为(-)+=(>0)

7已知、在抛物线:=2(>0)上，点(,)是抛物线上一定点，且⊥⊥，求点的轨迹方程，并说明它表示什么曲线

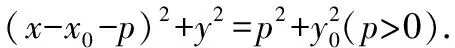
8已知，在抛物线:=2(>0)上，点(,)是抛物线上一定点，=⊥，求点的轨迹方程，并说明它表示什么曲线

上述探究又转到了另一个层面，把问题引申到纵向，完全体现问题研究的多样性，既保持主要元素的不变性，又体现多元性只有把握住可变要素，才能做出精彩的探究，提出更精彩的问题

(四)横向探究

从抛物线上看，完成证明还是比较容易的，但是变为椭圆、双曲线后，猜想结论成立，构建命题比较容易，证明过于繁杂，只有勇于探究，一定能取得完美证明

设直线:=(+),

得(+)+2+-=0，

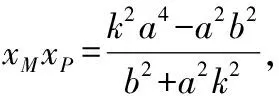
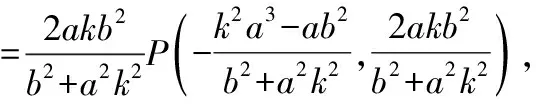
-2(1-)=(+)(+)+-)，(+)(+)

=-2(1-)-(+)(-)(+)(+)

=-(-)(+)

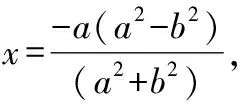
(-，0)，(，)，(，)，

得：(+)+2+-=0，

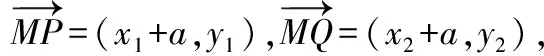
(+)(+)+=0，

(+)(+)+(+)(+)=0，

(1+)+(+)(+)++=0

(1+)(-)-2(+)

+(+)(+)=0，

(+)-2-(-)=0，

[(+)-(-)](-)=0,

代入直线:=+，得：

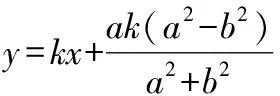
以下变式可让学生课外小组进行研究虽然证明过程、方法更为复杂，但是能够吸引学生做深入研究，使学生获得成就感

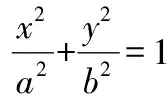
11过圆锥曲线上的一定点(,)作两互相垂直的弦、，若非等轴双曲线，则必过定点；若为等轴双曲线则直线必有定向

证明可仿上

抛物线:=2，定点(+2,-)

12过圆锥曲线(双曲线、非等轴双曲线)上的一定点(,)任作两互相垂直的弦，，联结，过作的垂足，则点在定圆上

方法略，模仿抛物线可完成

设(，)，(，)，直线:=+,

得：(+)+2+-=0，

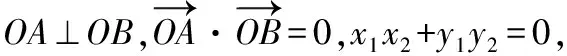
+(+)(+)=0，

(1+)++=0，

(1+)(-)-2+(+)=0

-+--2++=0,

--+=0，

(+)-(1+)=0，

∵||||=||||,

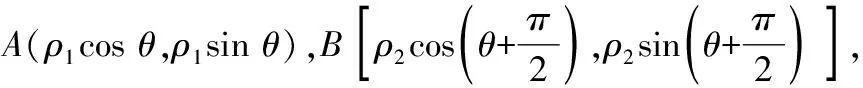
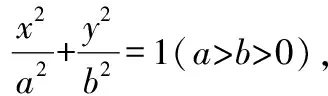
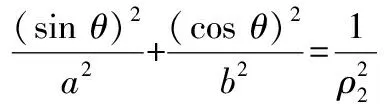
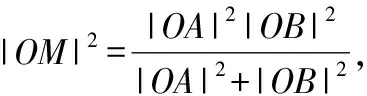
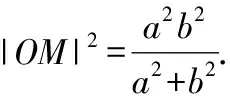
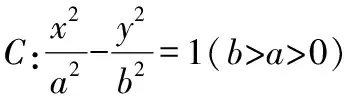
随着新一轮的课程改革，研究性学习已经走进课堂，研究性试题也开始进入高考试题中教师应鼓励学生敢于提出问题，积极构建问题场景，创建新的学习平台、学习方式，培养创新型、研究型人才落实探究教学，还课堂研究氛围，活跃学生思维，提高提出问题、解题问题、探究问题的能力，培养学生学习兴趣，提高数学研究能力