从“浮力消失实验”探究判断浮力的关键因素
缪昳闻,童大振,潘苏东
华东师范大学教师教育学院,上海 200062
1 问题的提出
2021年12月9日下午,王亚平、翟志刚、叶光富在中国空间站进行了“太空授课”,借助太空中天然的微重力环境,展示了神奇的、与地面上不同的物理实验现象,其中第二个实验是“浮力消失”实验。在地面上,乒乓球会漂浮在水面上,无法被按入水中;而在太空舱中,乒乓球没有浮上水面,而是“安静地”待在水中,看起来好像就是浮力消失了。王亚平对此现象的解释很简单:“太空舱中没有重力,因此没有浮力”。
那么,重力和浮力之间是否确实构成简单的因果关系呢?
2 地空重力的差异
2.1 在地面上重力等于万有引力吗?
万有引力是两个质点之间在任何情况下都存在的相互吸引的力。在地面上进行实验时,通常将地球视作惯性系,认为物体所受重力就是万有引力。然而,由于地球的自转,它并不是精确的惯性系,还需要考虑离心惯性力的作用。因此,物体在地面上受到的重力实际上是万有引力和离心惯性力的合力,此时合力方向不是指向球心,而是存在一个偏角α(图1)。

图1 物体在地球表面的受力示意图


此时,离心惯性力远小于万有引力,且偏角α远小于1°。因此,可以近似认为重力就是万有引力,其公式化为G=F=mg,其中常数g的大小代表了地球对物体的吸引程度,是地球引力场的场强,由地球参数决定,数值约为9.8 N/kg。
2.2 为什么中国空间站是微重力环境?
重力是指由于地球的吸引而使物体受到的力。若忽略地球自转的影响,物体在地面附近受到的重力就等于它受到的万有引力。中国空间站距地表d≈400 km,小于地球半径的十分之一,可以近似认为在地表附近。该距离下的地球引力场场强:

与地表引力场场强g≈9.8 N/kg相比仅减小了约10%,远没有小到可以忽略不计的程度。理论上在空间站中的物体会受到地球的万有引力作用,也就是说“重力”不为零。因此,我们一般描述的空间站的“微重力环境”实际上并不是指重力为零,而是因为在转动的非惯性系中,物体受到的是离心惯性力与地球对它的万有引力的合力,即为“视重”,此时其视重为零。
对于中国空间站而言,它是在地球的万有引力作用下绕地球做轨道绕转,是一个非惯性参考系。不同于地表的物体,它的绕转不是由地球自转所带动的,绕转周期和地球自转周期不同;在绕转时,空间站受到的离心惯性力与地球对它的万有引力的合力为零,故其视重为零。
3 地空浮力差异的关键——视重的大小
3.1 地球上的浮力产生原因是什么?
在地球上,物体浸在液体中会受到浮力是由于物体上下表面受到的液体压力不等,底部受到的向上的压力大于顶部受到的向下的压力,从而体现为受到一个竖直向上的合力,称之为浮力。而物体不同位置受到的液体压力不等则是由液体内部压强差造成的:

在地球上,受到地球的吸引,所有的液体分子都会受到向下的重力作用,地球的吸引体现为重力场场强g这一物理量。由于液体分子在容器内的堆叠,处在越深位置的液体分子受到上方液体分子的压力就越大,而液体的流动性将这一压力沿各个方向传递,在单位面积上体现为液体内部压强,因此同种液体内部压强随着深度的增加而增加,在竖直方向上的不同位置便会产生压强差:

对于上述结论,形状规则和形状不规则的物体都适用。
假设有一规则的长方体[图2(a)],物体上下表面积均为S,上表面距液面h,此处液体内部压强 p=ρgh,下表面距液面 H,此处液体内部压强p=ρgH,则上下表面受到的液体压力差为:

图2 不同物体浸没在液体中的情形
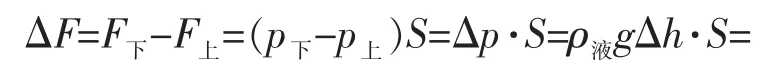

而对于不规则物体[图2(b)],利用微分的思想可以沿竖直方向将其分解为无数个极细的柱体,对于每个柱体上下表面的面积都是相等的,因此将每个柱体受到的液体压力差相加即为整个物体受到的液体压力差。进行公式推导可以得到相同的结论:
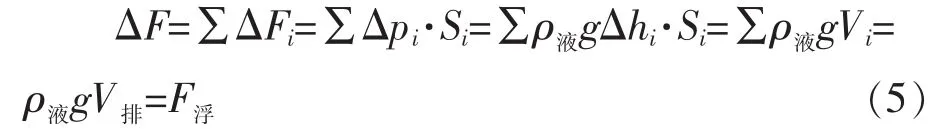
3.2 中国空间站内为什么不存在浮力?
对于中国空间站的微重力环境而言,“视重”为零意味着任一物体对其支持物的作用力都为零。因此,在竖直方向上液体分子不会因堆叠而产生累加的压力,此时液体内部压强处处为零,且在液体内部不存在压强差。液体内部压强差为零意味着物体上下表面受到的液体压力差也为零,因此在空间站内,液体对物体不产生浮力作用,“视重”为零,浮力也为零。
反观地面上的情况,实验时整个系统处在惯性系内,此时视重等于重力。因此,看似是液体分子受到重力最终导致浮力的产生,实际上“视重”不为零才是地面上浮力不为零的关键,同时也是地空浮力差异的关键所在。它们的关系如图3所示。
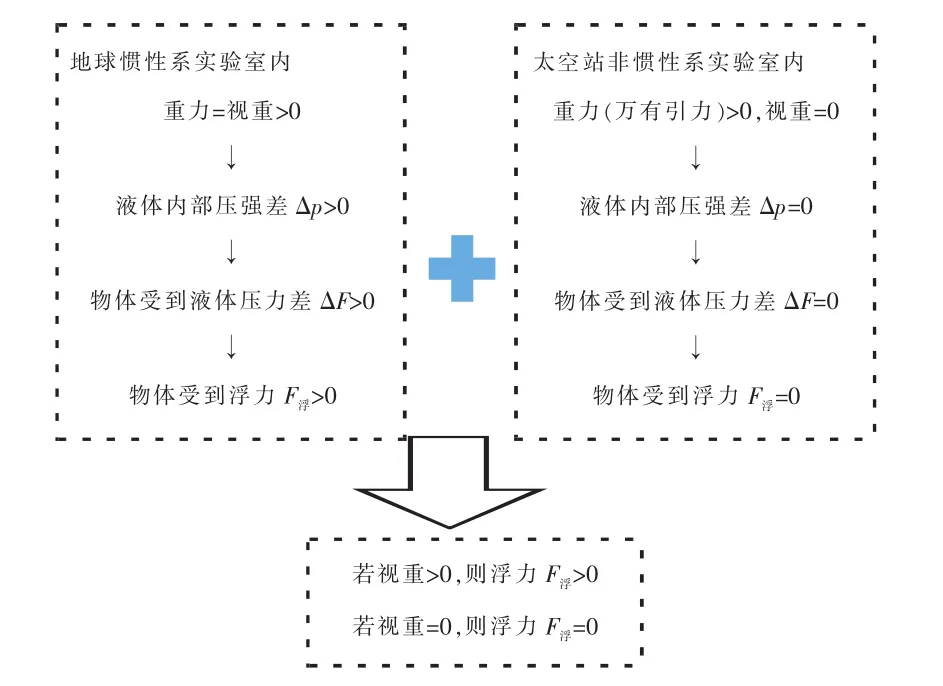
图3 视重与浮力关系的逻辑推导
4 对王亚平解释的深入分析
王亚平在天宫课堂中通过“……浮力是随重力产生的……”解释了“浮力消失”的原因,这有利于中学生对初学浮力产生更深刻的认识。但站在更高的角度可以发现,浮力存在与否,并非完全由重力决定。
(1)首先,在地面上,物体确实处处都受到重力,但并非在任何情况下都受到浮力。若在地球上让浮力实验的整个系统做自由落体运动,液体受到的重力不变,但此时“视重”为零,因此液体仍然不对乒乓球产生浮力作用。
(2)另一方面,结合重力的定义以及我国空间站距地表的距离,空间站内物体并非因为“无重力”而“无浮力”,而是由于空间站的绕转,这部分重力(即地球的万有引力)与离心惯性力互相平衡,导致“视重”为零,从而导致浮力为零。
5 结论的一般性推广
知道了视重的大小便可以判断浮力是否存在。然而,视重的大小并不直观,因此还需了解视重的大小与较为直观的物体运动状态之间的关系。现将物体所处环境分为“存在引力场”与“无引力场”两种情况进行讨论。
5.1 引力场中物体运动状态与“视重”大小的关系
若系统处在引力场作用范围内,除了要考虑引力场的吸引作用,还要考虑物体所处系统在该引力场中的运动状态。也就是说,需要综合考虑引力场场强g(N/kg)和加速度a(m/s)。
在地球上时,物体的超重、失重状态具有如表1中所示的性质。

表1 不同超重、失重状态下对应的视重与加速度
将以上性质迁移至一般星球引力场中,将“视重>重力”和“视重<重力”合并为“视重>0”,并规定引力场场强g的方向为正,如表2所示。
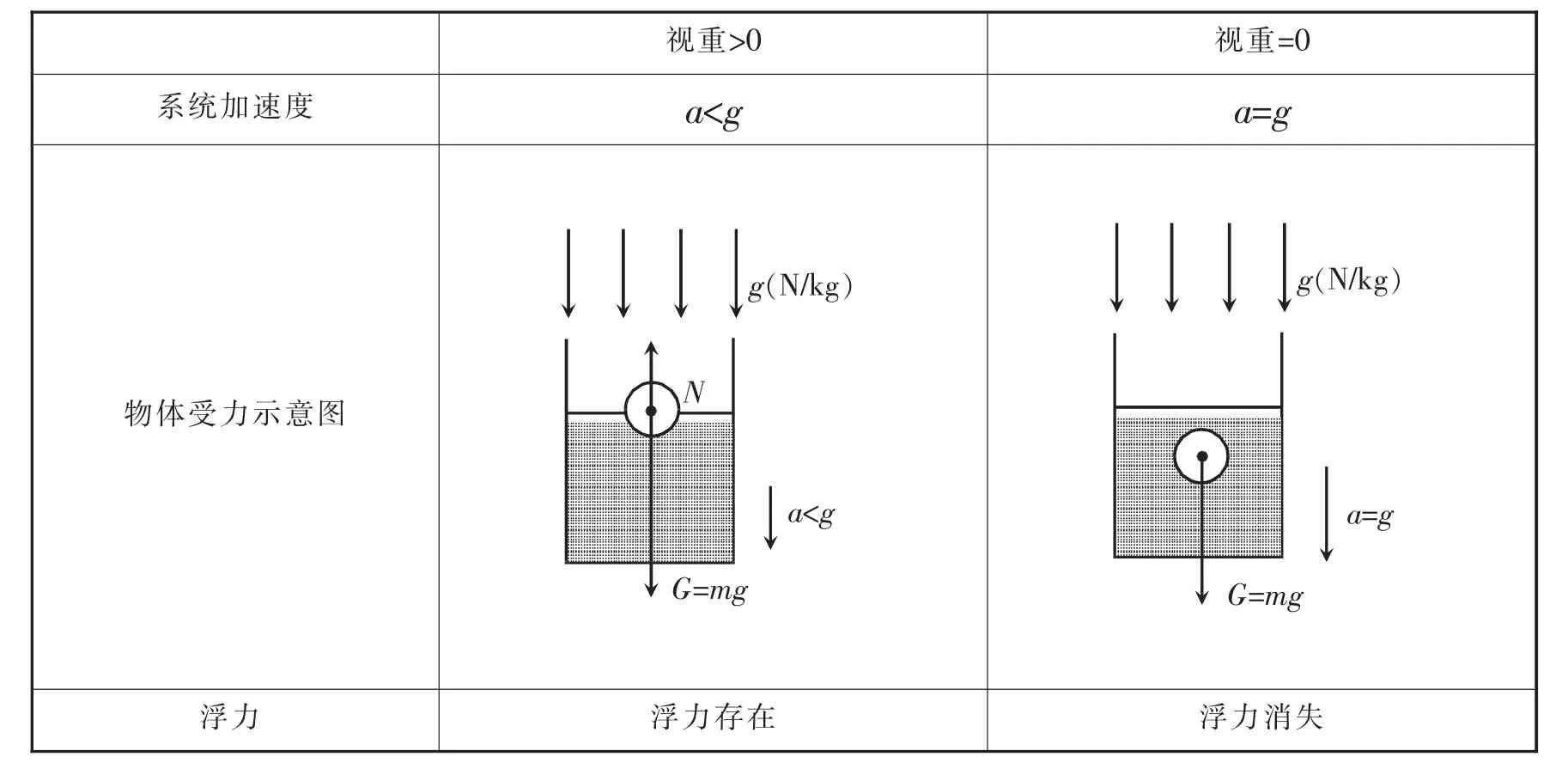
表2 引力场中视重大于零和等于零时系统对应的加速度与引力场场强的关系
在引力场中,当系统满足a<g时,系统中物体的视重大于零,浮力存在;当系统满足a=g时,系统中物体的视重为零,浮力消失。
特别地,当视重为零,加速度等于引力场场强时,存在两类情形。第一类是在引力场中做“自由落体运动”,此时物体处在直线加速型非惯性系内,万有引力与惯性力平衡;第二类是在万有引力作用下围绕星球做绕转,此时物体处在转动型非惯性系内,万有引力与离心惯性力平衡。
5.2 无引力场环境中物体运动状态与“视重”大小的关系
爱因斯坦在解释广义相对论中的等效原理时曾提及:加速度a(m/s)和引力场场强g(N/kg)所带来的作用效果是相同的。他用两个电梯思想实验来解释这一观点:“在封闭的电梯里,人们无法判断到底是在有引力的情况下处于静止,还是在没有引力的情况下做加速运动。”
也就是说,在无引力场环境中一个被加速的实验室中的物理学和一个静止在均匀引力场中的实验室中的物理学是一样的;与上述等效相类似的,静止在无引力场环境中的实验室中的物理学和在均匀引力场中自由下落的实验室中的物理学是一样的。前者对应的是物体“视重>0”,后者对应的是物体“视重=0”。
如表3所示,假设浮力实验在水杯中进行,规定水杯杯底朝向为正方向,杯口朝向为负方向:

表3 无引力环境中视重大于零和等于零时系统对应的加速度
在无引力场环境中,当系统满足a<0时,系统中物体的视重大于零,浮力存在;当系统满足a=0时,系统中物体的视重为零,浮力消失。

