定量探究向心加速度影响因素的创新实验装置

汪小明

深圳市宝安第一外国语学校，广东 深圳 518128

1 研究背景

1.1 教材分析

新人教版和新粤教版高中物理必修第二册在介绍向心加速度的公式时，都是采用了先通过图1所示的实验器材探究得出向心力的表达式，然后再结合牛顿第二定律得出向心加速度的表达式，都没有直接通过实验定量探究出向心加速度的表达式。另外，该实验装置较为复杂，实验原理让学生较难理解，定量探究精确度不高，实验结果说服力不强。

图1 向心力演示器

虽然在新人教版教科书“拓展学习”栏目中介绍了“推导向心加速度公式”的方法，但是采用的是数学中的极限思想进行推导（图2），这种数学的方法对学生的抽象思维能力要求较高，学生不容易理解。即使是在老师的引导下推导得到了向心加速度的表达式，学生可能还是会对表达式心存疑惑。

图2 向心加速度公式推导示意图

1.2 改进实验装置的必要性

物理学是一门以实验为基础的学科，物理概念的建立、规律的得出，最好是能通过观察实验现象、分析实验数据、总结实验规律，最终得到准确可靠的实验结论，这样更符合学生对客观事物的认知规律。因此，改进实验器材，优化实验方案，提高实验结果的准确度具有非常重要的研究价值和实践意义。

1.3 传感器简介

如图3所示，本创新实验装置采用的传感器是维特智能9轴蓝牙5.0姿态角度传感器（型号为BWT901BLE5.0），体积小巧，应用方便。该传感器内置模块集成了高精度的陀螺仪、加速度计等传感器，能够快速求解出模块当前的实时运动状态。通过蓝牙稳定地将向心加速度、角速度等数据实时传输至电脑端，并以文本文档的形式存储。

图3 传感器实物图

2 实验器材及实验装置图

本实验装置包含的实验器材有：维特智能姿态角度传感器（以下简称传感器），蔬菜脱水篮，特制刻度尺，无痕双面胶，电脑及Excel软件。实验装置如图4所示。

图4 实验装置图

3 实验原理

将两端带有卡槽的特制刻度尺水平放置于蔬菜脱水篮内部直径处，使刻度尺“0”位置位于脱水篮圆心正上方的位置。通过无痕双面胶将传感器粘在刻度尺上某一位置，使传感器的x轴指向圆心，y轴与半径垂直。转动脱水篮，使传感器和刻度尺跟随脱水篮一起做圆周运动。传感器将采集到的向心加速度与角速度等数据通过蓝牙实时传输至电脑端，并以文本文档的形式存储。利用Excel软件打开文档，选取传感器上x轴向心加速度和y轴角速度的数据进行研究。以角速度ω为横轴，向心加速度a为纵轴，插入散点图，得到的a-ω图像是一条过原点的抛物线；以角速度的平方ω为横轴，向心加速度a为纵轴，插入散点图，得到的a-ω图像是一条过原点的倾斜直线，说明向心加速度a与角速度的平方ω成正比。

改变传感器的转动半径，重复刚才的实验过程，得到的a-ω图像仍然是一条过原点的倾斜直线，并且直线斜率随着半径的改变而变化。当把向心加速度、角速度、半径等物理量的单位统一成国际单位时，直线斜率恰好等于传感器的转动半径。

如此，通过实验探究，定量得到了影响向心加速度因素的表达式 a=ω·r。

4 实验过程

4.1 建立数据连接

开启传感器电源，通过电脑蓝牙与传感器进行匹配，在电脑端打开传感器配套的软件界面，在“设备列表”栏中点击“搜索”按钮，在呈现的设备列表中选择名称为“WT901BLE68”的设备建立数据连接，传感器采集的向心加速度、角速度等数据便实时显示在软件界面上。

4.2 传感器“0”位置校准

将传感器粘贴在刻度尺的“0”刻线位置上方，转动脱水篮，观察软件中x轴向心加速度a的数值。若a不为0，则微调传感器在刻度尺上的位置，再次转动观察，直到a=0时，将刻度尺“0”刻线对应的传感器位置做上标记，此位置即为传感器的“0”位置。

4.3 采集实验数据

将传感器粘贴在刻度尺上某一位置，如图5所示（为了在实验中转动半径有更多的取值，首次实验时转动半径r取较小值）。在电脑端软件上点击“记录”菜单中的“开始”按钮，让传感器开始记录并存储数据。接着以随机的速度转动脱水篮，让传感器的角速度尽可能取到不同的数值，记录到一定量的数据后点击“停止”按钮，采集到的数据将会自动保存在电脑上。

图5 将传感器置于刻度尺上

4.4 处理实验数据

用Excel软件打开采集到的实验数据，该实验数据包含了数据采集的时间，x、y、z三个轴上的加速度、角速度、角度等物理量。提取其中x轴的向心加速度（系统默认显示为“加速度X”）、y轴的角速度（系统默认显示为“角速度Y”）的数据，复制到事先编辑好单位换算公式的数据处理表格中，表1为带公式的数据处理表格。

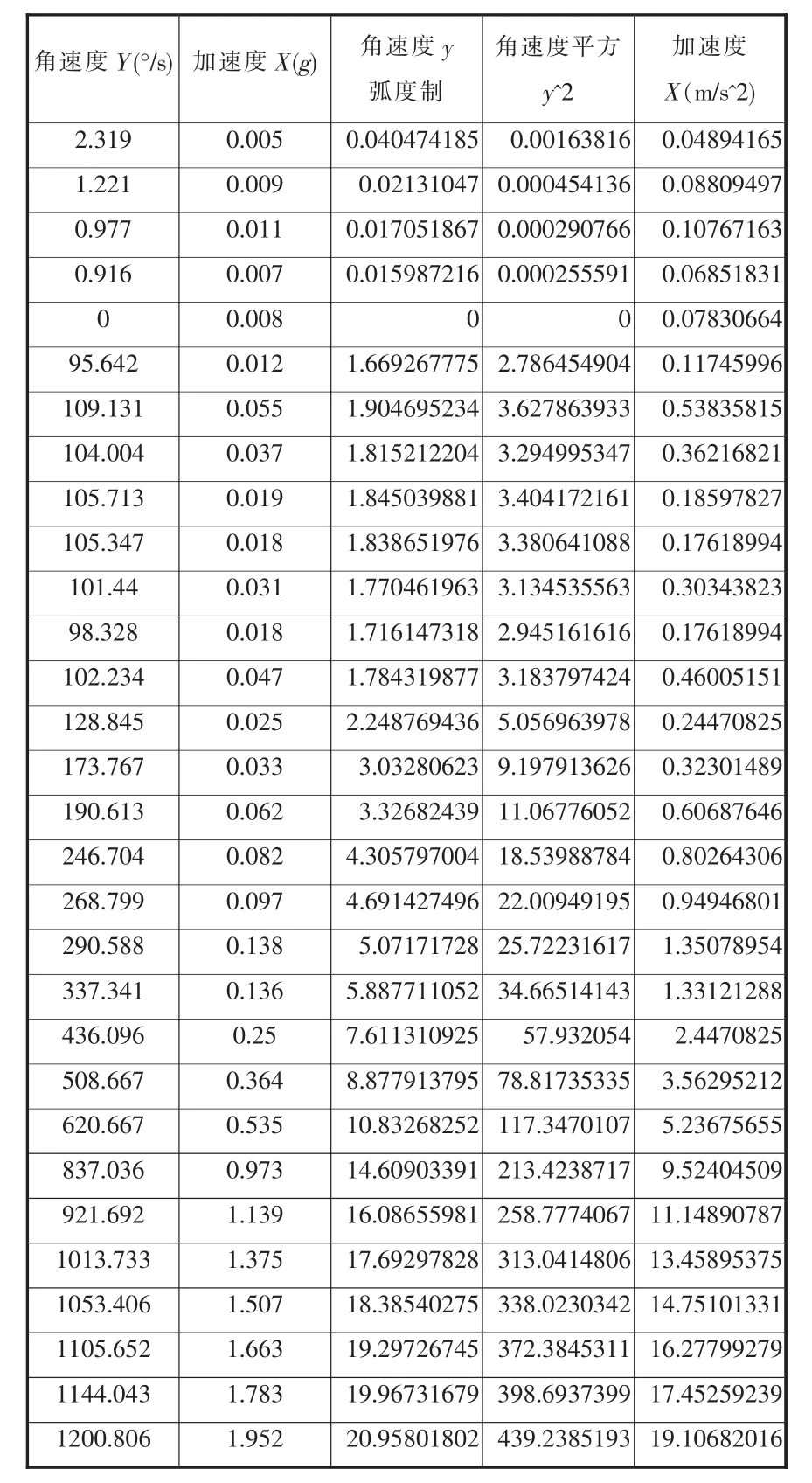
表1 带公式的数据处理表格

4.5 Excel拟合图像

以角速度ω为横轴，向心加速度a为纵轴，插入散点图，描绘出a-ω图像（图6）。该图像近似为一条过原点的抛物线，由此可以合理猜测向心加速度a与角速度ω呈二次函数的关系。

图6 a-ω图像

4.6 改变横轴拟合图像

以角速度ω的平方为横轴，向心加速度a为纵轴，插入散点图，描绘出a-ω图像（图7）。该图像恰好为一条通过原点的直线，说明向心加速度a与角速度平方ω成正比。

图7 a-ω2图像

4.7 改变转动半径再次实验

改变传感器在刻度尺上的位置，重复此前步骤，可得到不同转动半径下的a-ω图像、a-ω图像。图8为转动半径r=0.0437 m的a-ω图像和a-ω图像；图9为转动半径r=0.0536 m的a-ω图像和a-ω图像。通过Excel中趋势线选项显示直线公式，发现传感器的转动半径恰好与其对应的a-ω图像直线的斜率相等。

图8 半径为r2=0.0437 m的a-ω图像和a-ω2图像

图9 半径为r3=0.0536 m的a-ω图像和a-ω2图像

实验结论：由a-ω图像为一条过原点的倾斜直线可知，向心加速度a与角速度的平方ω成正比，再结合直线的斜率等于半径，可得a=ω·r。至此，我们通过这套创新的实验装置，成功地完成了向心加速度影响因素的定量探究实验。

5 实验误差分析

5.1 偶然误差

传感器“0”位置校准时，标记传感器“0”刻线时会产生误差；依据刻度尺读取转动半径的数值时会存在读数误差。

5.2 系统误差

维特姿态角度传感器测量加速度的最大数值为16g，测量角速度的最大值为2000°/s，因此在转动脱水篮时，角速度和加速度的数值不宜过大。若是超过了加速度和角速度的最大测量值，传感器就无法输出准确的数值，加速度会错误地输出16g，角速度会错误地输出 2000°/s，这些错误的数据会对本实验的图像产生影响，从而导致产生系统误差。

6 实验装置的优点及改进方向

6.1 装置的优点

（1）直接通过实验探究定量得出向心加速度的表达式。

（2）将用数学方法推导物理量表达式转化为通过物理实验探究得到物理量表达式，体现了物理学科的实验特色，同时也起到了化难为易的教学效果。

（3）本实验装置的成本较低，取材方便，实验操作简单，数据采集容易。

（4）本实验数据拟合的图像为一条过原点的倾斜直线，图像形象直观，准确度高，说服力强。

6.2 改进方向

（1）改用餐桌上的圆形转盘替代蔬菜脱水篮，让传感器的转动半径有更大的可调范围；同时，也让传感器在实验过程中直接呈现在学生面前，在整个实验过程中全程可见，增加本实验的观赏性。

（2）编写可视化的数据处理应用软件，通过手机屏幕实时显示a-ω图像，优化数据处理环节，增强实验数据的视觉效果。

7 结束语

2019年2月中共中央、国务院印发了《中国教育现代化2035》，在部署的战略任务中，明确提出了加强课程教材体系建设，充分利用现代信息技术，丰富并创新课程内容和形式。本创新实验装置借助了小巧灵活的加速度、角速度传感器开展定量探究实验，优化了实验方案，降低了学习难度，可以很好地引导学生经历科学探究过程，体会科学研究方法，培养学生的科学思维品质，是现代信息技术与物理实验教学深度融合的成功案例，同时也是对物理教科书中现有实验方案的有益补充。