非常规运动图像的特征与解题应用

王玉琴

(山东省淄博市周村区第一中学)

在匀变速直线运动公式v2－＝2ax中,由v、x的函数关系和a、x的函数关系,可得到v2-x、x-v2、x-v、a-x4类运动图像,下面我们讨论4类图像的相关分析方法和解题应用.

1 v2-x 图像

由公式v2－v20＝2ax,得v2＝2ax＋v20,可知匀变速直线运动v2-x图像(如图1)为倾斜直线,斜率等于2a;图线与v轴的交点坐标等于初速度的平方v20;图线与x轴的交点坐标等于x0＝

图1

例1某自主品牌的一款无人驾驶汽车在直线测试时的速度平方与位移关系v2-x图像如图2所示.自经过x＝0位置时开始计时,则该车在2s内的位移大小为( ).

图2

A.2.0m B.2.6m

C.3.0m D.3.6m

根据图像由v2－v20＝2ax,知v2＝2ax＋v20,故图像的斜率k＝2a,故该车运动的加速度大小a＝5m·s－2,初速度大小v0＝6m·s－1,由t＝＝1.2s可知,该车1.2s后停止,得2s内的位移x＝＝3.6m.选项D 正确.

2 x-v2 图像

由公式v2－v20＝2ax,得x＝,可知匀变速直线运动x-v2图像(如图3)为倾斜直线,斜率等于;图线与纵轴的交点坐标为x0＝

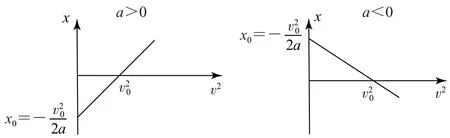
图3

例2如图4-甲所示,一维坐标系中有一质点静止于x轴上的某位置(图中未画出),从t＝0时刻开始,质点在外力作用下沿x轴正方向做匀变速直线运动,其位置坐标与速率平方关系的图像如图4-乙所示.下列说法正确的是( ).

图4

A.物块运动的加速度大小为1m·s－2

B.t＝4s时物块位于x＝2m 处

C.2～4s时间内物块平均速度大小为1.5m·s－1

D.前2s时间内物块的位移大小为2m

3 x-v 图像

由公式v2－v20＝2ax,得x＝,可知匀变速直线运动x-v图像(如图5)为曲线的一部分.

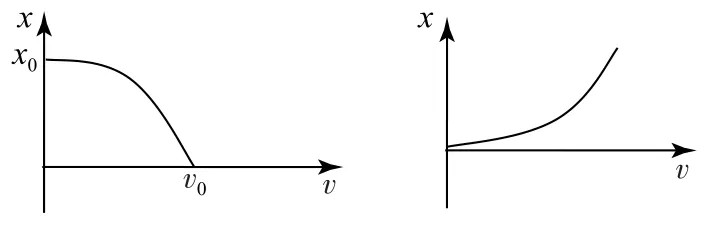
图5

例3行驶中的汽车遇到红灯刹车后做匀减速直线运动直到停止,等到绿灯时汽车又重新开始做匀加速直线运动直到恢复原来的速度,再做匀速运动.关于汽车从刹车到恢复原速度的过程,以下位移随速度变化的关系图像正确的是( ).

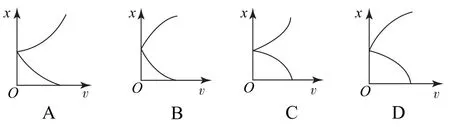
由v2－v20＝2ax,可得x＝,汽车先做减速运动,所以减速过程a为负值,故图像应为开口向下的二次函数图像.汽车由速度为零开始做加速运动时v2＝2a(x－x0),其中x0是停止时的位置坐标,上式变形得x＝x0,a为正值,故图像为开口向上的二次函数图像.故选项C正确,选项A、B、D 错误.

例4甲、乙两质点同时从x＝0 处出发沿x轴正方向做匀变速直线运动.甲、乙运动速度v与位移x的关系如图6 所示,其中甲的图线为抛物线的一部分(该抛物线顶点在坐标原点且关于x轴对称),乙的图线为与x轴平行的直线.由图可知,下列说法正确的是( ).

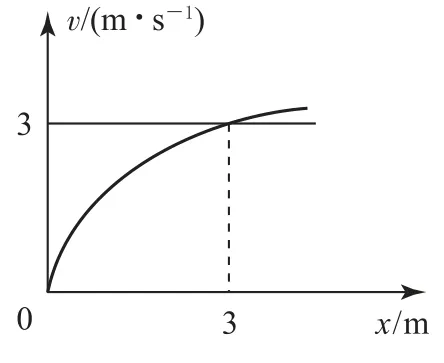
图6

A.甲做加速度为1m·s－2的匀加速直线运动

B.出发后1s,甲速度大小为3m·s－1

C.两质点在x＝3m 处相遇

D.两质点相遇时,甲速度大小为6m·s－1

对甲质点根据v2－＝2ax,可知x＝当v＝0时,该抛物线顶点在坐标原点,且图像过(3,3),代入解得a＝1.5m·s－2,故选项A 错误;出发后1s,甲速度大小为v＝at＝1.5m·s－1,故选项B错误;在x＝3m 处,甲速度达到3m·s－1,需要时间为2s,此时间内,乙做匀速直线运动,其位移为x＝v乙t乙＝6m,此时未相遇,故选项C错误;两质点相遇时,v乙t＝,解得t＝4s,此时甲速度大小为v＝at＝6m·s－1,选项D 正确.

4 a-x 图像

由v2－＝2ax可知a-x图像(如图7)与坐标轴所围图形面积表示

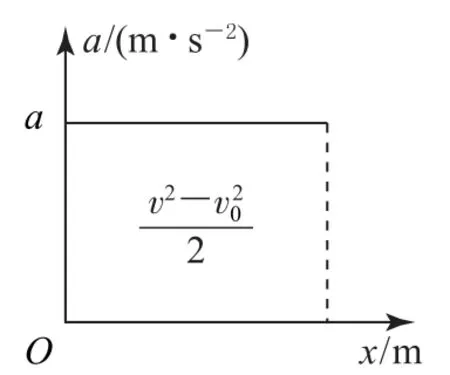
图7

例5工人利用轻质动滑轮提升建筑材料的情景如图8-甲所示.绕过轻滑轮的轻绳一端固定,通过拉动另一端使水桶由静止开始竖直上升,两侧轻绳始终保持竖直,水桶的加速度a随水桶上升的高度h的变化关系如图8-乙所示.以下说法正确的是( ).

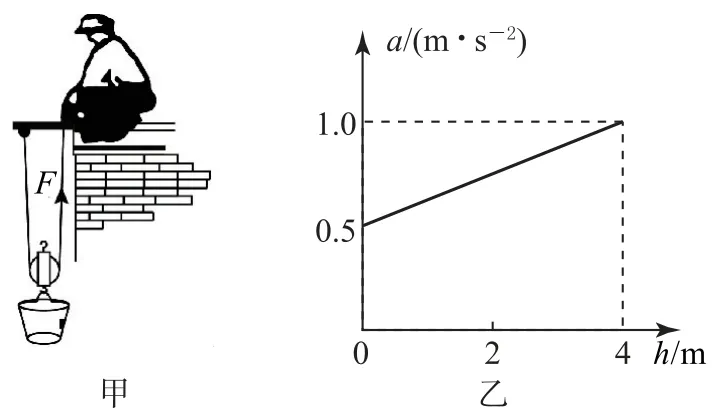
图8

由题可知v2＝2ah,结合图像面积可得水桶上升4m 时的速度大小v＝m·s－1＝·s－1,故选项A 正确.

由以上分析可知,不论遇到什么样的运动图像,得出图像的数学表达式,观察和推导图像的斜率、截距、面积的物理意义,都是解题的关键和突破口.

(完)