问题引领促深思,数理通融育素养
——以匀变速直线运动的中间位置速度为例
程贤楼
(安徽合肥市第七中学)
问题1如图1所示,一物体由A到B做匀变速直线运动,O为AB的中点,物体在A、B点的瞬时速度分别为v1、v2,则物体在O点的瞬时速度该如何表示呢?
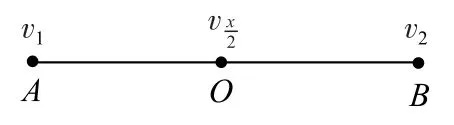
图1
分析设线段AB的长度为x,物体的加速度为a,由匀变速直线运动速度与位移的关系可得

问题2物体做匀变速直线运动的速度—时间图像是一条倾斜的直线.以匀加速直线运动为例,其v-t图像如图2所示,其中OABC梯形的“面积”表示物体速度由v1变为v2过程中的位移,平行于v轴的线段DE把梯形“面积”二等分,因此为物体中间位置的瞬时速度,即.从数学角度来说,即,你能从数学角度来证明此结论吗?

图2
分析由于图2中OABC为直角梯形,我们在直角梯形中证明此结论.
如图3 所示,在直角梯形OABC中,OA∥DE∥BC,DE把梯形面积二等分.现要证明


图3
如图4所示,延长CO、BA,它们相交于点P,设PO=h0,OE=h1,EC=h2,OA=a,BC=b,DE=c.

图4
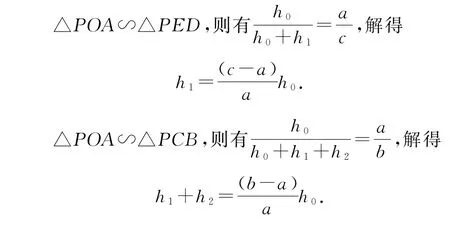
又因为DE把梯形OABC面积二等分,则梯形OADE的面积为梯形OABC面积的一半,即
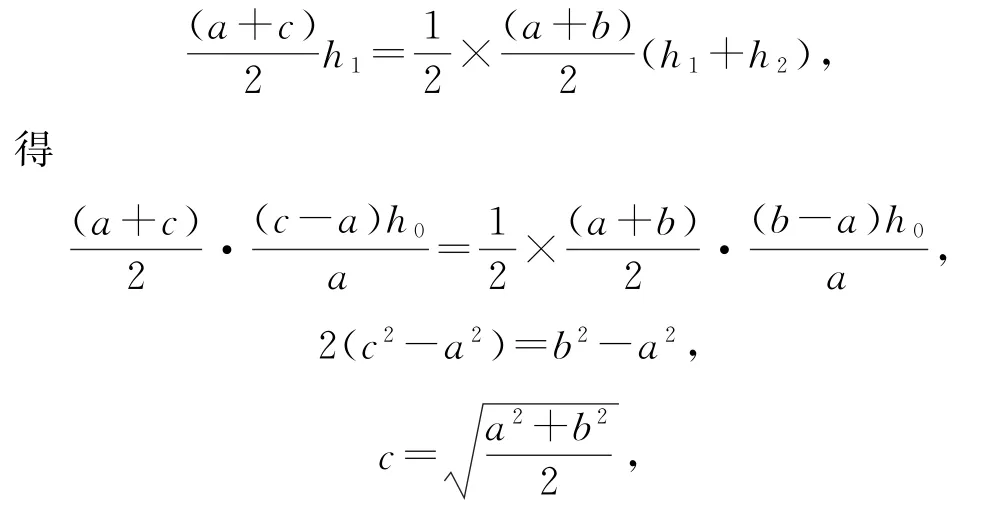
得证.
问题3在直角梯形中,平行于底边的线段DE把梯形面积二等分,则DE=,在一般梯形中该结论也成立吗?
分析如图5所示,在一般梯形OABC中,OA∥DE∥BC,DE把梯形面积二等分,现要证明

图5

如图6所示,延长CO、BA,它们相交于点P,过点P作线段PK垂直于底边BC,PK与OA、ED分别相交于点F、J.设PF=h0,FJ=h1,JK=h2,OA=a,BC=b,DE=c.
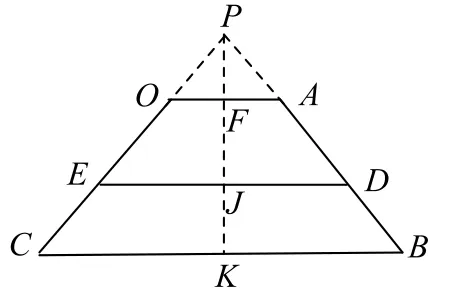
图6
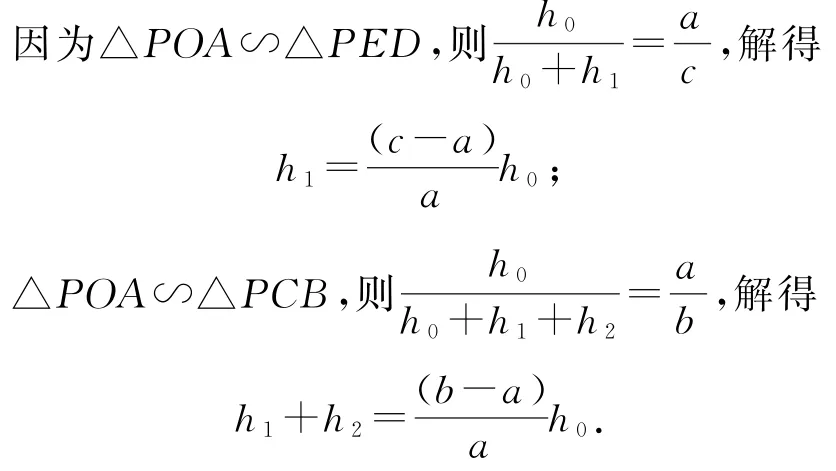
又DE把梯形OABC面积二等分,则梯形OADE的面积为梯形OABC面积的一半,即

得证.
问题4如图7所示,给你一个梯形,你能用尺规作图的方法作一条平行于底边的线段,使得该线段把梯形面积二等分吗?
图7
分析如图8所示,作图步骤如下:

图8
(1)延长CO、BA,它们相交于点P,过点P作线段PK垂直于底边BC;PK与OA相交于点F;
(2)过点P作PQ∥BC,且PQ=PK;
(3)连接FQ,作FQ的垂直平分线分别交FQ、PQ于点M、N;
(4)在线段PN上取点G,使得PG=GN;
(5)以点G为圆心,GQ为半径画圆交PK于点J;
(6)过点J作ED∥BC,ED即为所求线段.线段ED把梯形OABC面积二等分.
证明 如 下:设PK=PQ=l,NQ=NF=r,△POA的面积为S0,梯形OADE的面积为S1,梯形EDBC的面积为S2.
在△PNF中有
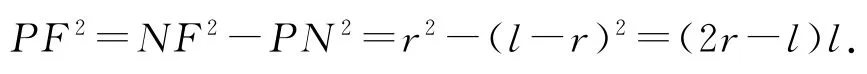
在△PGJ中有
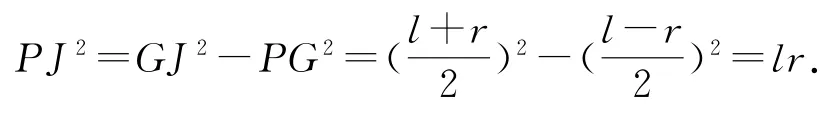
△POA∽△PED,则
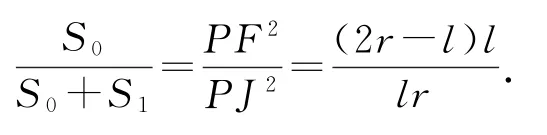
△POA∽△PCB,则
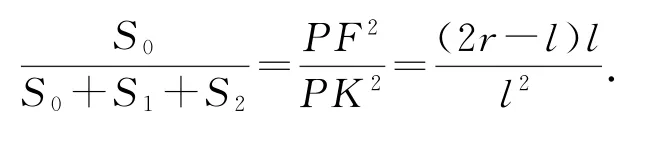
由以上两式解得S1=S2=,得证.
【小结】物理和数学联系非常紧密,中间位置的瞬时速度既可用物理知识推导,也可用数学知识推导.本文先从物理学公式推导出匀变速直线运动中间位置的瞬时速度,再通过位移—时间图像把中间位置的瞬时速度和梯形面积的二等分线联系起来,从数学角度来验证物理公式,还作出并验证了梯形面积的二等分线.
(完)

