概率论与数理统计在医学中的应用

李大伟

(上海立信会计金融学院统计与数学学院 上海 201620)

2019年12月，一场突如其来的新型冠状病毒肺炎(COVID-19)疫情打破了我们平静的生活，随后迅速席卷全球。时至今天，已有数百万人死于新冠病毒。新冠疫情的爆发严重影响了人们的工作、学习、生活以及健康，对全球经济以及世界格局更是产生了无法估量的影响。新冠肺炎作为一种急性呼吸道传染病，研究它的发生、发展、诊断、预防以及治疗等方面能够帮助我们抓住疾病的薄弱环节，采取有效的措施，达到更好的防控效果。本文我们将从概率论与数理统计的角度对新冠疫情中的一些问题进行分析与研究。

1 新冠肺炎隔离期问题

潜伏期，是一般疾病在发展过程中的一定阶段，这一阶段是从致病刺激物侵入机体或对机体发生作用起，到机体出现反应或开始呈现症状时止。不同传染病的潜伏期时间不同，同一种传染病在不同个体之间的潜伏期也是不同的。很多疾病在潜伏期的某个节点开始都是具有传染性的，而不是等潜伏期结束了才具有传染性。潜伏期是传染病的重要传播动力学参数之一，是确定检疫(包括医学观察、留验和集体检疫)时间的重要依据，在制定传染病防控策略与措施、评价防控措施效果及预测流行趋势中均具有重要意义[1]。

新冠疫情暴发初期，专家们通过对部分病例进行跟踪分析与研究。根据收集到的数据做出一条曲线，确定95%的置信区间，然后经过反复试验和观察确定最长的时间间隔是14天，从而把隔离期定为14天。对于传染病的潜伏期，常见的分布有对数正态分布(Log-normal)、伽马分布(Gamma)和韦伯分布(Weibull)[2-4]。杜志成等[5]利用区间删失数据估计方法，通过比较Log-normal、Gamma和Weibull分布，对新冠肺炎的潜伏期分布进行估计，得到Gamma分布具有较大的对数似然函数值，从而得出Gamma分布可能是COVID-19潜伏期的最优分布，潜伏期M=5.064(P25～P75：3.489～7.304)天。从概率论与数理统计角度证明了把新冠隔离期定为14天是合理的。

2 核酸检测问题

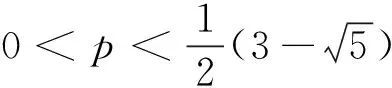
虽然混合检测法可以更高效的获取检测结果，但是要把多少个样本混合在一起进行检测也是我们需要考虑的一个重要问题。严加安院士在“概率破玄机，统计解迷离”中提到，假设已知人群的患病率为p，要对N个样本进行混合检测时，通过概率计算可得平均检测总次数为N/k[qk+(k+1)(1-qk)]，其中q=1-p，k代表每组混合的样本数量，从而我们可以通过计算机确定最佳的k值。李榕[8]同样从概率论角度对混合检测的样本数量进行了分析，得出当把10个样本放在一起进行检测时的效果最好，而实际上武汉部分区域正是一次性将10个样本放在一起进行了混合检测。

3 新冠诊断问题

例1. 根据医学数据分析，假设某次新冠肺炎核酸检测以95%的概率将新冠患者检查出呈阳性，但也有2%的概率误将非新冠患者检查出呈阳性(“假阳性”)。若某一特殊群体患新冠肺炎的概率为0.05%，求

(1)其中一个个体新冠病毒核酸检测结果为阳性的条件下，他确实患病的概率(确诊率)是多少？

(2)如果“假阳性”的概率降为0.2%，0.02%和0时，确诊率如何变化？

(3)重复检测能否提高确诊率？

解：记A={核酸检查结果为阳性}，B={检查者患新冠肺炎}，

已知P(B)=0.0005

P(A|B)=0.95

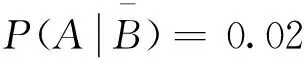
根据贝叶斯公式可得

因此，一次检测结果为阳性的条件下，实际患病的概率仅为2.32%。

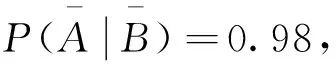
也是非常高的(一般诊断价值LR>20就认为很高了)，但是此处P(B|A)的值却很小，这是为什么呢？其实主要原因就是因为新冠的患病率P(B)=0.0005远小于检测错误率。针对此处情形，通常会进行多次独立重复的复查。

(3)在(1)中我们得到即使核酸检测结果是阳性，实际患病率仅为2.32%。

针对此种情形，我们通常会进行多次独立重复的复查。设Ai={第i次核酸检查结果为阳性}，i=1,2,3, ..., n。此时由贝叶斯公式可得

即两次核酸检测都是阳性者，患新冠的可能性为53.02%，相对于第一次检测，准确性提高了接近23倍。如果我们继续做第三次检测，此时P(B|A1A2A3)≈0.9817。由此可见，若三次核酸检测都是阳性，患新冠的可能性就非常大了。当然，因为这里题目中都是一些假设的数据，与实际情况可能会存在一些差距，但是根据上述理论分析我们可知，一次核酸检测阳性并不能说明一定患病，通常需要经过多次独立重复检测，并配合一些其他项目的检查，才能最终做出判断。

4 药物疗效的问题

自疫情暴发以来，为了有效的控制疫情，遏制疫情的蔓延，各国都在努力研发新冠疫苗以及治疗药物。任何一种新药从研发到投产，中间都要经过许多的试验和评估等措施，接下来我们从概率论角度对药物疗效相关问题做简单分析。

例 2. 假设新冠患者自然痊愈率为0.3，医院检查员任意抽查100名注射某种疫苗的患者。根据相关部门规定，如果治愈患者数超过75人，则判定疫苗是有效的；否则，判定疫苗无效。试求

(1) 疫苗治愈率为0.8，但被判定无效的概率是多少？

(2) 疫苗无效，但被判定有效的概率是多少？

解：设X={治愈患者数}，由题意知

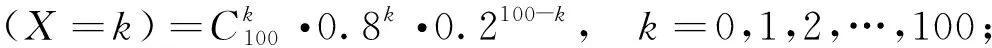
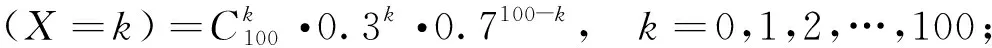
(1)当疫苗治愈率为0.8时，根据题意分析可知，如果实际治愈患者人数不超过75人，则被判定为无效，此时概率为

(2)疫苗无效，此时的治愈率为自然痊愈率0.3，根据题意分析可知，如果实际治愈患者人数超过75人，则被判定有效，此时概率为

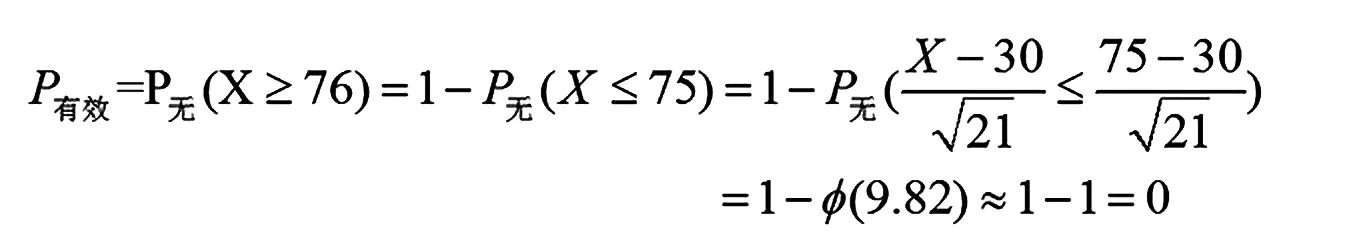
5 总结

综上所述，概率论与数理统计在医学中具有非常广泛的应用。本文我们主要以新冠肺炎为例，从概率论与数理统计的角度对其中的相关应用做了简单介绍。期望通过这些理论分析，可以帮助我们采取更高效的措施去防控疫情。