关于对坐标的曲线积分若干问题研究

齐小军

(天水师范学院 数学与统计学院 甘肃 天水 741001)

0 引言

积分是大学数学的重要内容，在高等数学中积分又分为定积分，重积分，曲线积分和曲面积分等．曲线积分是其中的一个难点，其内容抽象，计算方法多样．曲线积分又分为对弧长的曲线积分和对坐标的曲线积分，很多文献[4-7]对这类积分做过较为细致的研究．在高等数学中，随着积分内容的深入，积分之间联系越来越密切，难度也在加大．本文主要讨论对坐标的曲线积分的计算，以及探讨在计算中的简便方法．

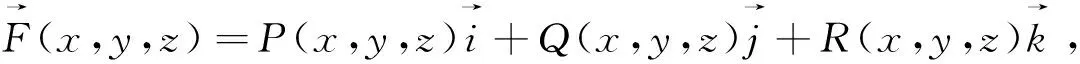
1 一般曲线上的对坐标的曲线积分

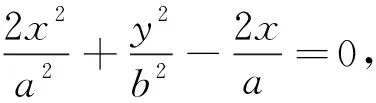
在上述问题中，我们也可以通过坐标系的旋转，将问题化为某一坐标面上的定积分．通过坐标旋转有时还可将曲线化作较简单曲线，简化计算．

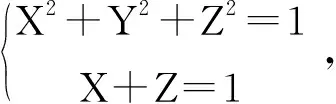
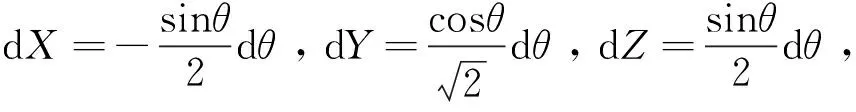
通过做坐标系的旋转，在新的坐标系下使曲线变为较简单的曲线方程，对曲线方程引入参数方程，计算过程相对简单，这不失为一种新的处理曲线积分问题的方法．在某些情况下可考虑这种方法．

将曲线积分转化为某一参量的的积分，这里的计算会依赖于曲线方程的简易程度，也可以转化为对变量x或变量y的定积分．一个自然的想法是能否将对不同坐标的积分转化为对其中一个坐标的曲线积分．

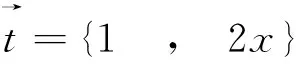
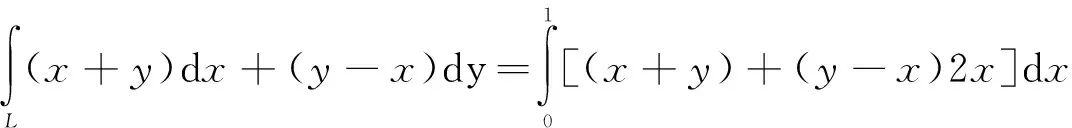
同样也可转化成对y坐标的积分，计算难易程度相同．对于上述积分如果通过两类曲线积分间的等式转变成对面积的曲线积分，其最终还是化成了对某一变量的定积分，这跟上述作法如出一辙．反过来，如果将对弧长的曲线积分转化成对坐标的曲线积分，在这种情况下可能简化计算过程．

2 封闭曲线上的对坐标的曲线积分

前面，我们将曲线积分转变为定积分，同样也可转化成重积分．假设区域D由分段光滑的曲线L围成，函数P(x,y)，Q(x,y)在闭区域D上有一阶连续的偏导，则有Green公式

[2]，其中L是D的取正向的边界曲线．

问题2 计算

其中L是沿曲线y=x2由点A(1,1)到点O(0,0)的一段．

在y轴的点B(0,1)处连接OB,AB．于是可得由曲线y=x2以及坐标轴y和直线段y=1所围成的一个二维封闭图形D，在区域D上使用Green公式，于是有

在直线段AB上dy=0，于是

-6-e.

在直线段BO上dx=0，于是

=sin1

由Green公式

于是I=-3-e+sin1.

同样，上述问题也可利用积分与路径无关的条件转化成折线路径求解．

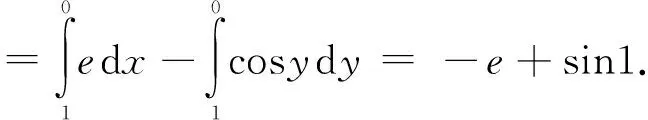
而积分

由此，利用恰当条件可使计算简化，当然这种方法适合区域D是单连通域，并且满足积分与路径无关的条件．

前面我们将平面闭曲线上的曲线积分转化成重积分，但对于空间闭曲线上曲线积分，我们可以将其表示成空间曲面上的曲面积分．利用Stokes公式就可将曲线积分表示成曲面积分．在某些情况下，这样的做法可极大的简化计算过程．

其中，Γ为分段光滑的空间有向曲线，Σ是以Γ为边界的分片光滑的有向曲面并且Γ的正向与Σ的侧符合右手法则．

问题3 计算积分

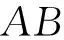
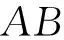
上述问题同样也可利用空间曲线积分与路径无关的条件，转变为恰当方程求解．

(z2-xy)dz成立．于是积分

可以看出，使用恰当方程解题过程更简单．

至此，我们讨论了关于对坐标的曲线积分在两种曲线类型下计算的部分问题，包括曲线积分转化为定积分，曲线积分的向量形式，两类曲线积分的相互转化，曲线积分和重积分以及曲线积分和曲面积分之间相互转换，曲线积分在二维平面闭区域，三维空间区域上积分与路径无关问题的计算，每一种问题的解决方法都有各自的特点，可以看出曲线积分跟积分曲线，被积表达式的关系密切．同一种问题用多种方法都可以加以解决，但处理的过程有难易区别．在使用这些方法时要注意他们各自适用的条件．也可以通过被积函数的奇偶性，曲线的对称性等灵活处理．