斯蒂尔杰斯矩量问题产生探源

李 威 曲安京

(1.西北大学科学史高等研究院，西安 710127； 2.西安财经大学统计学院，西安 710100)

矩量问题理论起源于连分数，它对概率论、算子理论和矩阵论等理论的交叉融合有重要作用。斯蒂尔杰斯矩量问题是矩量问题的开始，对其产生的历史过程进行研究，有助于我们理解矩量问题理论整体发展脉络，促使我们用全局化视野考量矩量问题在数学统一化发展过程中的作用。目前已有文献对矩量问题的某些片段做出一些研究。克莱茵(Morris Kline，1908—1992)在《古今数学思想》中指出：为了表示一个解析函数序列的极限，斯蒂尔杰斯(Thomas Jan Stieltjes，1856—1894)引入了斯蒂尔杰斯积分，这是积分概念的第一次扩充[1]；笔者对里斯(Friedrich Riesz，1880—1956)在不同函数集中的矩量问题进行研究，找出了连续函数集和勒贝格平方可积函数集之间的区别和联系，这是矩量问题在分析学中的一个应用[2]；著名的数学家和数学史家迪厄多内(Jean Dieudonné，1906—1992)和皮埃奇(Albrecht Pietsch)对里斯处理矩量问题的方法给予了细致的论述，指出矩量问题与哈恩-巴拿赫定理之间的联系[3，4]。克杰森(Tinne Hoff Kjeldsen)通过介绍矩量问题的发展历程，对矩量问题与连分数的分析理论之间的关系进行介绍，重点剖析了矩量问题脱离连分数理论的原因[5]。

近现代数学史的研究，可以从以前大家熟悉的关注历史上的数学成就“是什么”和“如何做”的视角，扩张到“为什么数学”的研究范式中来[6]。值得注意的是，基于“为什么数学”的研究方法，国内的近现代数学史研究工作者，已经从原始文献着手，提出并解决了一些具体的“真问题”[7—12]。

本文从数学发展的内部规律及思想传承出发，发现一些问题，如：连分数与斯蒂尔杰斯积分及矩量问题之间的思想传承是什么；连分数理论是如何脱离矩量问题的；斯蒂尔杰斯积分的概念是基于什么样的背景提出的，它的出现对矩量问题的产生有何推动作用。鉴于此，本文从原始文献和研究文献出发，详细探寻了斯蒂尔杰斯矩量问题的内部发展规律，并试图回答上述问题，以期得到一些有意义的结果。

1 斯蒂尔杰斯连分数理论

矩量问题的起源可以追溯到连分数收敛的一些问题，斯蒂尔杰斯运用前人的研究结果，探讨连分数与发散级数之间的关系，发现正实数集上的矩量问题与黎曼积分的不适用性，这促使了斯蒂尔杰斯对黎曼积分的首次推广。斯蒂尔杰斯对连分数和发散级数之间关系的证明，是推动其构建斯蒂尔杰斯积分和矩量问题的动因。

1.1 斯蒂尔杰斯对连分数理论探究的动因

要了解斯蒂尔杰斯的矩量问题，首先要探讨他的连分数理论，该问题与发散级数有关。1821年，柯西(Augustin Louis Cauchy，1789—1857)认为发散级数的和是无法表述的，当时的数学家对发散级数的研究格外小心[13]。但是，在物理学，特别是天体力学中，发散级数的应用却非常广泛，这一奇怪现象促使一些数学家对发散级数产生了浓厚兴趣，斯蒂尔杰斯便是其中之一。

斯蒂尔杰斯的科学研究生涯始于荷兰莱顿天文台，他非常熟悉发散级数在天体力学中的应用，为此他还对发散级数的用法做了总结，并于1886年以篇名《关于一些半收敛级数的研究》发表[14]。对发散级数的研究，使他了解到发散级数可以转换为连分数，这是他对连分数理论产生兴趣的原因。对此，瑞士数学家欧拉(Leonhard Euler，1707—1783)在早前也给予说明，他指出：

发散级数可以转换为连分数，反之亦然。([15]，页74)

可以看出，斯蒂尔杰斯将研究内容从发散级数延拓到连分数理论是数学发展的自然导向。与此同时，数学家拉盖尔(Edmond Nicolas Laguerre，1834—1886)证明：

在极限条件下，连分数问题与积分问题可以相互转化。[16]

沿着这一思路，斯蒂尔杰斯从由积分生成的无穷级数开始，利用矩量问题，将其与连分数联系起来。从这一过程可知，对发散级数的研究，是斯蒂尔杰斯研究连分数理论和矩量问题的一个诱因。下面是斯蒂尔杰斯的具体做法。

1.2 斯蒂尔杰斯连分数理论

1889年，斯蒂尔杰斯写信给埃尔米特(Charles Hermite，1822—1901)说：“我总是想到连分数。”([17]，页191)一个月后，他又表明：“连分数仍然困惑着我。”([17]，页215)斯蒂尔杰斯与埃尔米特的通信内容反映出，1889年他就已经开始研究连分数。

从上面的表述可以知道，连分数的敛散性取决于该连分数的系数级数的敛散性，这就可以将研究连分数敛散性的问题转化为与之对应的系数级数的敛散性问题。

为了证明上面的结论，斯蒂尔杰斯首先利用“斯蒂尔杰斯-维塔利”定理并证明，对于任意的正实数z，连分数的偶次渐近分数和奇次渐近分数将分别收敛于解析函数F(z)和F1(z)。关于“斯蒂尔杰斯-维塔利”定理，斯蒂尔杰斯描述如下：

根据我的定理容易得出如下结论，除负半轴之外，在整个实数轴上，连分数S(z)收敛。这是我寻求了很长时间的重要理论改进。([17]，页399)

此时，斯蒂尔杰斯遇到了不确定矩量问题。当时，他并没有立即给出矩量问题的概念，利用黎曼积分对其进行定义也是不恰当的。但此时，他已经发现导致矩量问题产生的关键问题。

斯蒂尔杰斯通过构建连分数的渐近分数来研究连分数与发散级数之间的关系，由于连分数的渐近分数可以扩展为无穷幂级数，进而可以将连分数的敛散性问题与无穷幂级数建立联系。利用“斯蒂尔杰斯-维塔利”定理可以证明连分数的奇次渐近分数和偶次渐近分数分别收敛于两个极限函数，在求解这两个极限函数的积分表达式的过程中会出现两个不相等的正值函数其“矩量问题”相等，并且这两个极限函数用黎曼积分来表达存在错误。这两个发现是斯蒂尔杰斯推广黎曼积分和探究矩量问题的诱因。斯蒂尔杰斯积分的产生过程如下。

2 斯蒂尔杰斯积分的产生

斯蒂尔杰斯很好地理解连分数的渐近分数及其渐近分数的极限形式之后，这部分内容也顺理成章地成为其研究的要点。除实数的负半轴之外，斯蒂尔杰斯利用“斯蒂尔杰斯-维塔利”定理，证明了连分数的渐近分数的收敛性，并给出其极限的解析形式。但由于黎曼积分的局限性，他在找出F(z)和F1(z)的解析形式时出现错误。为解决这个问题，斯蒂尔杰斯将黎曼积分的概念进行了扩展，这是斯蒂尔杰斯积分产生的原因。

2.1 斯蒂尔杰斯的错误

你是一个很棒的几何学家，你向我传达的有关连分数的研究结果是发明创造的典范；高斯和雅克比都没有给我带来这么多快乐。([17]，页350)

斯蒂尔杰斯之前表明，连分数的极限函数可用黎曼积分表示。但是由于极限函数可以表示成简单分数之和，而简单分数之和却无法表示成黎曼积分，因此用黎曼积分表示连分数的极限函数是错误的。

那么这就会产生另一个问题，为什么斯蒂尔杰斯会想到将连分数的极限函数表示为黎曼积分形式，其实原因有两点，一是极限的性质，二是该积分形式可以转化为斯蒂尔杰斯连分数。为了更正这一错误，斯蒂尔杰斯利用阶跃函数定义了斯蒂尔杰斯积分。

2.2 斯蒂尔杰斯积分的产生

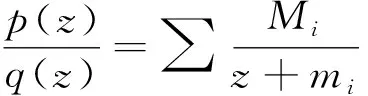
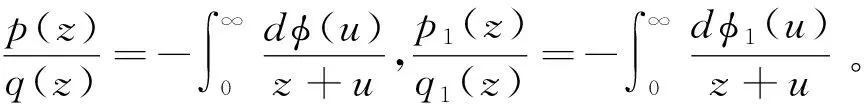
这是我上面提到的积分概念的推广；其中函数φ(x)是沿同一方向变化(该函数可能是不可导的，甚至在任意区间上都不连续)。([17]，页351)

为了能够用一个积分来表示连分数的收敛函数，斯蒂尔杰斯利用简单分数的展开，定义单调递减函数，利用该单调函数给出一个新的积分形式，就是我们现在所说的斯蒂尔杰斯积分。这是黎曼积分的首次推广，为积分理论向更广泛的方面发展提供可行性探测。

对于现代读者来说，以斯蒂尔杰斯的方式定义积分其实就是积分概念的自然推广，但在1892年的数学界，这种推广并不容易理解。从埃尔米特给斯蒂尔杰斯的信中以看出这一点：

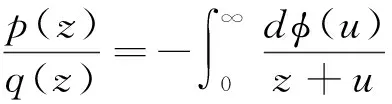
从埃尔米特提出的问题来看，他当时并不完全理解斯蒂尔杰斯为什么这样定义积分及他想利用该积分干什么。

人们通常认为，斯蒂尔杰斯引入积分是为了解决矩量问题，但直到现在，他也未提到矩量问题；上面的内容可以很清楚地表明，斯蒂尔杰斯扩展积分是为了找到连分数的解析形式，并给出其积分表达式。这表明斯蒂尔杰斯对积分的推广仍然停留在连分数理论的范畴之内。

此时斯蒂尔杰斯研究的侧重点仍是连分数理论，而非矩量问题。直到其学术生涯末期，才开始将矩量问题作为一个独立的理论来分析，并对不确定性矩量问题的一些特殊解进行了描述。那么存在一些问题，矩量问题在他的连分数理论中的作用是什么，是什么样的问题促使其开始深入研究矩量问题。这些都是我们下面需要解决的问题。

3 斯蒂尔杰斯矩量问题

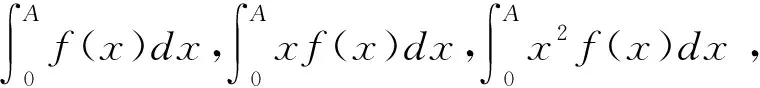
从这段描述来看，切比雪夫将矩量问题与积分极限问题建立了联系，并运用其解决未知密度的线上某一点的质量问题，该方法是受比奈先生报告的启发。从切比雪夫原文来看，此时他考虑的都是有限矩量问题，且仅仅把矩量问题当作证明伯努利定理的工具，并没有将其看作单独的数学理论进行深入研究[19]。

我们前面已经了解到，斯蒂尔杰斯对矩量问题的研究似乎仅仅停留在运用方面。尽管如此，从1893年9月他写给埃尔米特的信中仍可看出，他已经意识到矩量问题这一矛盾现象，并对该问题进行了尝试性探索。他给埃尔米特的信中写道：

我们把矩量问题称为：求直线(0，∞)上正质量分布的给定k阶矩(k=0，1，2，3，…)。([18]，页449)

即质量分布(Mi，mi)和(Ni，ni)，是系数级数收敛时，连分数S(z)所对应的矩量问题的解。利用这两个解，通过凸线性组合，可以构造无穷多个解，这可能是斯蒂尔杰斯将该问题称为“矩量问题”的原因。

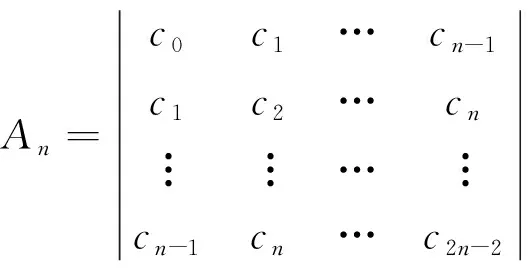
可以看出，斯蒂尔杰斯利用斯蒂尔杰斯积分，通过矩量问题的确定性，可以将探究连分数敛散性问题转换为判定其对应的行列式是否大于零的问题。这样就可跳过连分数，直接将矩量问题与无穷阶行列式对应起来。这是矩量问题脱离连分数理论的前兆，是后来的数学家把矩量问题作为独立理论进行研究的动因。这也反映了数学统一化发展的趋势。

4 结论

探寻斯蒂尔杰斯矩量问题的历史发展脉络，对研究连分数理论的历史、函数空间理论的形成及谱理论的历史发展过程具有极其重要的作用。通过对斯蒂尔杰斯矩量问题的历史进行研究，可以找出连分数、矩量问题和无穷级数之间的联系。斯蒂尔杰斯在探究连分数与发散级数之间的转化关系时发现，黎曼积分在简单分式上的“不适用性”，是斯蒂尔杰斯将黎曼积分拓展为斯蒂尔杰斯积分的动因。在主要定理的证明中，斯蒂尔杰斯发现了“斯蒂尔杰斯-维塔利”定理，并意识到非零函数的矩量问题为零的“特殊性”。为了解释这一“特殊性”，斯蒂尔杰斯给出了矩量问题可解性定义。然后，利用斯蒂尔杰斯积分和行列式的性质，将判定连分数的敛散性问题转化为与其对应的行列式是否大于零的问题，从而将矩量问题与无穷阶行列式直接对应起来，这是矩量问题脱离连分数理论的前兆，是无穷阶行列式应用于连分数理论的例子，是数学统一化发展的体现。对斯蒂尔杰斯矩量问题的研究，可以揭示斯蒂尔杰斯积分产生的原因，探明矩量问题与连分数理论之间的内在联系，进而更清楚地呈现矩量问题早期的发展脉络，为探寻其理论起源打下基础。