The energy conversion rates from eddies and mean flow into internal lee waves in the global ocean*

Bing HAN 1, 2, 3, 4, **

1 Laboratory for Coastal Ocean Variation and Disaster Prediction, College of Ocean and Meteorology, Guangdong Ocean University, Zhanjiang 524088, China

2 State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences,Guangzhou 510301, China

3 Institut für Meereskunde, Universität Hamburg, Hamburg 20146, Germany

4 Key Laboratory of Climate, Resources and Environment in Continental Shelf Sea and Deep Sea of Department of Education of Guangdong Province, Guangdong Ocean University, Zhanjiang 524088, China

Abstract Internal lee waves play an important role in transferring energy from eddies to small scale mixing. However, the energy conversion from eddies into lee waves in the global ocean remains poorly understood. Conversion rates from eddies and from mean flow in the global ocean were diff erentiated using single beam sounding data, stratification from climatology, eddy velocity, and mean flow from a global ocean model. The global integral energy conversion from eddies is estimated to be 0.083 TW and is almost twice as that from the mean flow. A new method was developed to study the uncertainties of energy conversion caused by dealing with the topographic data. Results show that diff erent data processing procedures, and the resolution and accuracy of topographic data have a significant impact on the estimated global energy conversion.

K eyword: internal lee waves; eddies; mean flow; energy conversion; topography

1 INTRODUCTION

The meridional overturning circulation (MOC)transports and redistributes mass, heat, salt, CO2, and nutrients around the globe, and has an important influence on the climate. Diapycnal mixing caused by wave breaking and other processes can bring the deep water to the ocean surface and plays a crucial role in sustaining the MOC. About 2 TW is needed for diapycnal mixing in the global ocean (Munk and Wunsch, 1998). The energy mainly comes from three types of motions: the near-inertial waves generated by winds in upper ocean, the internal tides generated by barotropic tides over bottom topography, and internal lee waves generated by geostrophic flows over bottom topography (Egbert and Ray, 2001; Alford, 2003;Garabato et al., 2004; Brearley et al., 2013; Rimac et al., 2013; Liu et al., 2019).

Mesoscale eddies are the largest kinetic energy reservoir in the global ocean, which can transport tracers and regulate global climate change (Ferrari and Wunsch, 2009). Eddies can be generated by barotropic and baroclinic instability, and dissipate through several processes. For example, they can dissipate through the bottom dissipation (Sen et al.,2008; Arbic et al., 2009), loss of balance (Molemaker et al., 2005; Polzin, 2010; Shakespeare and Taylor,2013, 2014, 2015; Shakespeare, 2019), interactions with other motions (Polzin, 2008; Zhang et al., 2020),generation of submesoscale motions and internal lee waves (Trossman et al., 2013; Melet et al., 2014;Trossman et al., 2015, 2016; Kunze, 2019; Yang at al.,2019). However, how much eddy energy dissipates through diff erent mechanisms remains poorly understood. Recently, the total energy flux into internal lee waves from geostrophic flow has been estimated and found to be about 0.2-0.94 TW based on linear theory (Nikurashin and Ferrari, 2011; Scott et al., 2011; Wright et al., 2014). In addition, Yang et al. (2018) estimated the energy loss of eddies due to lee wave generation (0.12 TW) in the Southern Ocean. However, the diff erence in energy conversion between from eddies and from the mean flow in the global ocean remains unclear.

Previous research has investigated the turbulent dissipation in the South Ocean, and found large diff erence between the observed dissipation rate and theoretical prediction of energy conversion rate oflee waves (Sheen et al., 2013; Waterman et al., 2013,2014; Cusack et al., 2017). For example, Waterman et al. (2013) showed that the conversion rate estimated by the linear theory (Nikurashin and Ferrari, 2011)was much larger than the observed dissipation rate in a region north of the Kerguelen Pkateau. These diff erences can be explained in many ways; for example, much of the energy may propagate away from the generation sites (Zheng and Nikurashin,2019), the linear theory may ignore some finite topography eff ects (Nikurashin et al., 2014), and there are limitations for the topographic spectrum(Nikurashin et al., 2014). Motivated by the diff erence between the observed dissipation rate and the energy conversion rate estimated by linear theory, the paper investigates whether diff erent data processing procedures on calculating the topographic spectra and topographic data resolution can have an important influence on the estimated global energy conversion,which has not been well investigated so far. In this study, new methods were developed to compute the energy conversion. Results show that the abovementioned factors could cause inaccuracies on the calculation of energy conversion in the global ocean.

This article is arranged as follows: in Section 2, the data and methods used for calculations are described;in Section 3, the energy conversion rates from the mean flow and eddies are computed; in Section 4, the uncertainties of energy conversion caused by dealing with the topographic data are discussed; The conclusions are shown in Section 5.

2 DATA AND METHOD

2.1 Theory

The energy flux transferred from geostrophic flows to internal lee waves in small-cale topography is given by (Bell, 1975; Nikurashin and Ferrari, 2011;Nikurashin et al., 2014),

To calculate the energy generation rate oflee waves from eddies and mean flow, the full velocity is divided into the time-mean flow and eddy velocity and the results are obtained by using Eq.1. This method is diff erent from the former research (Yang et al., 2018)in which they divided both the velocity and lee wave drag into their time-mean and transient components.They then calculated the energy loss from eddies and mean flow due to lee wave generation.

The key quantities in this calculation are the topographic spectra, topographic height, bottom stratification, and bottom velocity, which will be introduced in the next sections.

2.2 Topographic spectra

Following the method of Goff and Jordan (1998)and Nikurashin and Ferrari (2011), and assuming the topography is isotropic, the eff ective topographic spectrum in Eq.1 then can be calculated by

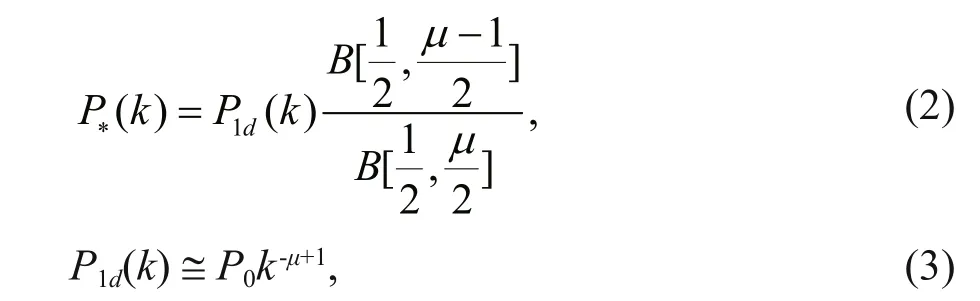
whereBis the Beta function,P1d(k) is a onedimensional form of model spectrum,P0is the spectral level given in terms of parameters of the twodimensional spectrum andμis the spectral slope.

Here,P1d(k) is computed using single beam sounding from U.S. National Geophysical Data Center’s Marine Trackline Geophysics database. The database provides access to bathymetry data collected during marine cruises from 1939 to the present and its coverage is worldwide. Data sources include global oceanographic institutions, universities, and government agencies. The resolution of the data in the Southern Ocean is smaller than that in the Northern Ocean.

The topographic spectra are estimated as follows.The single beam sounding depth data deeper than 500 m is divided into diff erent segments with a resolution of at least 2 km and a length of 50 km, the topographic slope is removed for each segment, then the along track topographic spectrum is calculated.Using Eq.3,P0andμare obtained in the 2 to 20 km wavelength range.

Due to the limitation of the spatial resolution of topographic data, the resolution of energy conversion rate is 3°×3°. There are two methods to calculate the energy conversion rate. The first method (hereinafter referred to as “RF”) (Nikurashin and Ferrari, 2011) is introduced as follows. The topographic spectra of diff erent segments over a 3°×3° grid are averaged,andP0andμare calculated in each grid. Then the conversion rate with a resolution of 3°×3° can be computed by usingP0andμ. Absent values due to lack of topographic data are estimated from neighboring grid cells.

In order to investigate whether diff erent data processing procedures can have a large influence on the results even for the same topographic data, a new method is developed to compute the conversion rate.The second method (hereinafter referred to as “RS”) is introduced as follows. Instead of averaging the topographic spectra over a 3°×3° grid,P0andμin each segment are calculated first; thenP0andμare divided into 3°×3° grid cells. Using the bottom velocity U,stratificationN,P0, andμfrom a 3°×3° grid cell, the conversion rates can be obtained in each grid.Moreover, by using this method, the mean conversion rate can be got by averaging the rates over the same grid, and the largest and smallest conversion rates can also be obtained by setting the rate as the maximum and minimum value within the same grid. The total number of about 225 000 segments is used.

2.3 Topographic roughness

The topographic roughness calculated from single beam soundings here is compared with the global abyssal hill rms heights (Goff and Arbic, 2010). The topographic roughness calculated from single beam soundings is defined in two ways.

whereris the spreading rate,h0is the uncorrected rms height, andSis the sediment thickness (Eden and Olbers, 2014). The spreading rates of the world’s ocean crust has a resolution of 2 min and covers all major ocean basins (Müller et al., 2008). The domain of NCEI’s (National Centers for Environmental Information) global ocean sediment thickness extends from 60°E to 155°E, and 30°S to 70°S (Whittaker et al., 2013). The rms data has 1° spatial resolution.Only part of areas of ocean hashrms＞ 0 using this method.

2.4 Bottom stratification

The global bottom stratification is calculated by the World Ocean Circulation Experiment (WOCE)Global Hydrographic Climatology (Gouretski and Koltermann, 2004) which has a 0.5° spatial resolution and 45 depth levels. The potential pressure, potential temperature, and potential salinity from the bottom two layers are used for the calculation.

2.5 Bottom velocity

Fig.1 Bottom stratification N using the WOCE hydrographic atlas

The bottom mean flow and eddy velocity are got from the global eddy-permitting STORM model (von Storch et al., 2012). The model was spun up for 25 years using the German Ocean Model Intercomparison Project (OMIP) forcing derived from the 15-year European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis (ERA-15). Then the model was run with the forcing of 6 hourly National Centers for Environmental Prediction(NCEP)-National Center for Atmospheric Research(NCAR) reanalysis-1 (Kalnay et al., 1996) for the period 1948-2010 with a resolution of about 1/10°, so it can achieve a quasi-steady state of mesoscale eddies. Further details of the model setup can be found in von Storch et al. (2012). Here the output of mean flow and eddy velocity are used, both of which have a resolution of 1°×1°.

3 RESULT

The values of bottom stratificationNare between 10-3.5s-1and 10-2.5s-1over most of areas with high values ofNin mid-ocean ridge and low values ofNover abyssal ocean (Fig.1). The values in the areas with a depth shallower than 500 m are not calculated.

The bottom mean flow kinetic energy (MKE) and eddy kinetic energy (EKE) show a similar pattern that they are enhanced in Antarctic Circumpolar Current(ACC) region, west boundary currents and equatorial regions (Fig.2). However, the EKE is larger than the MKE in most areas of the ocean, and its energy can be enhanced to 10-2m2/s2in ACC region, indicating the lee wave generation from eddies is larger than that from the mean flow.

The topographic roughness calculated by using two kinds of data is compared (Fig.3). The largehRF(Fig.3a) is along mid-ocean ridges where the process of seafloor spreading occurs, and it is enhanced up to 100 m. The small roughness is in flat abyssal plains that are covered by sediments.hRS(Fig.3b) shows a pattern similar to the Fig.3a, though the roughness is a little smaller. It is up to 80 m along mid-ocean. The diff erence betweenhRFandhRSis caused by diff erent calculation methods. In summary, most of areas of the ocean are covered with the topographic roughness of 0-100 m forhRFandhRS. The global abyssal hill rms heightshrms(Goff and Arbic, 2010) is shown in Fig.3c.Compared with thehRFandhRScalculated from the single beam soundings, it has a similar pattern and can be enhanced to more than 200 m.

The steepness parameter is determined by the bottom buoyancy frequency, topographic height, and bottom velocity. The steepness parameters calculated using the mean flow and eddy velocity from the global eddy-permitting STORM model are shown in Fig.4.The steepness parameter from the eddy velocity shows a pattern similar to that from the mean flow. In addition, it is also similar to the former results(Nikurashin and Ferrari, 2011). It is large in the areas with large bottom stratification or large topographic height, such as the equatorial regions and the midocean ridges (Fig.4), indicating the energy conversion in these areas should be corrected, while it is small in the ACC area because oflarge bottom current velocity.

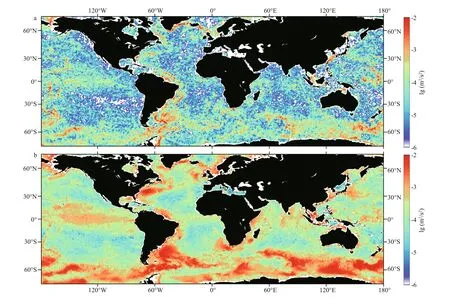
Fig.2 Bottom MKE (a) and bottom EKE (b)

The importance oflee wave generation from eddies is compared with that from the mean flow. By using RF and topographic heighthrange, the conversion rates from the mean flow and eddy velocity are calculated and shown in Fig.5. The rates from the eddy velocity and mean flow are large in the large currents areas and show a pattern similar to the bottom kinetic energy,indicating that the bottom current velocity plays a crucial role in the lee wave generation. Though these spatial patterns are also similar to these obtained by previous studies (Nikurashin and Ferrari, 2011; Scott et al., 2011; Wright et al., 2014), the diff erences exist due to diff erent bottom velocity data. The results also show that the rate from eddies is much larger than that from the mean flow, indicating that the lee wave generation is mainly from eddies instead of the mean flow. To better understand the diff erence in conversion rate between from eddies and from the mean flow, the rates are then integrated in the global ocean. Here the conversion rates in the areas with values larger than 2×102mW/m2are set to be 0 in order to inhibit large value. The energy conversion from the mean flow and eddies are 0.035 and 0.083 TW, respectively. Yang et al. (2018) pointed that the energy loss from eddies and mean flow due to lee wave generation in the Southern Ocean is 0.12 and 0.04 TW, respectively. The results that obtained in the paper are diff erent from Yang et al.(2018) because diff erent data have been used and calculations have been done using diff erent methods and diff erent velocity. However, both results highlight the importance oflee wave generation from eddies.

4 DISCUSSION

As we know, the terrain is a crucial factor for generating internal lee waves. The previous studies have obtained diff erent conversion rates by using diff erent topographic data and the rate is also influenced by the anisotropy in small-scale topography(Scott et al., 2011; Yang et al., 2018). In this section,the goal is to prove that even for the same topographic data, diff erent data processing procedures can obtain diff erent results, and insuffi cient data resolution will cause inaccuracies in calculating the global energy conversion oflee waves.

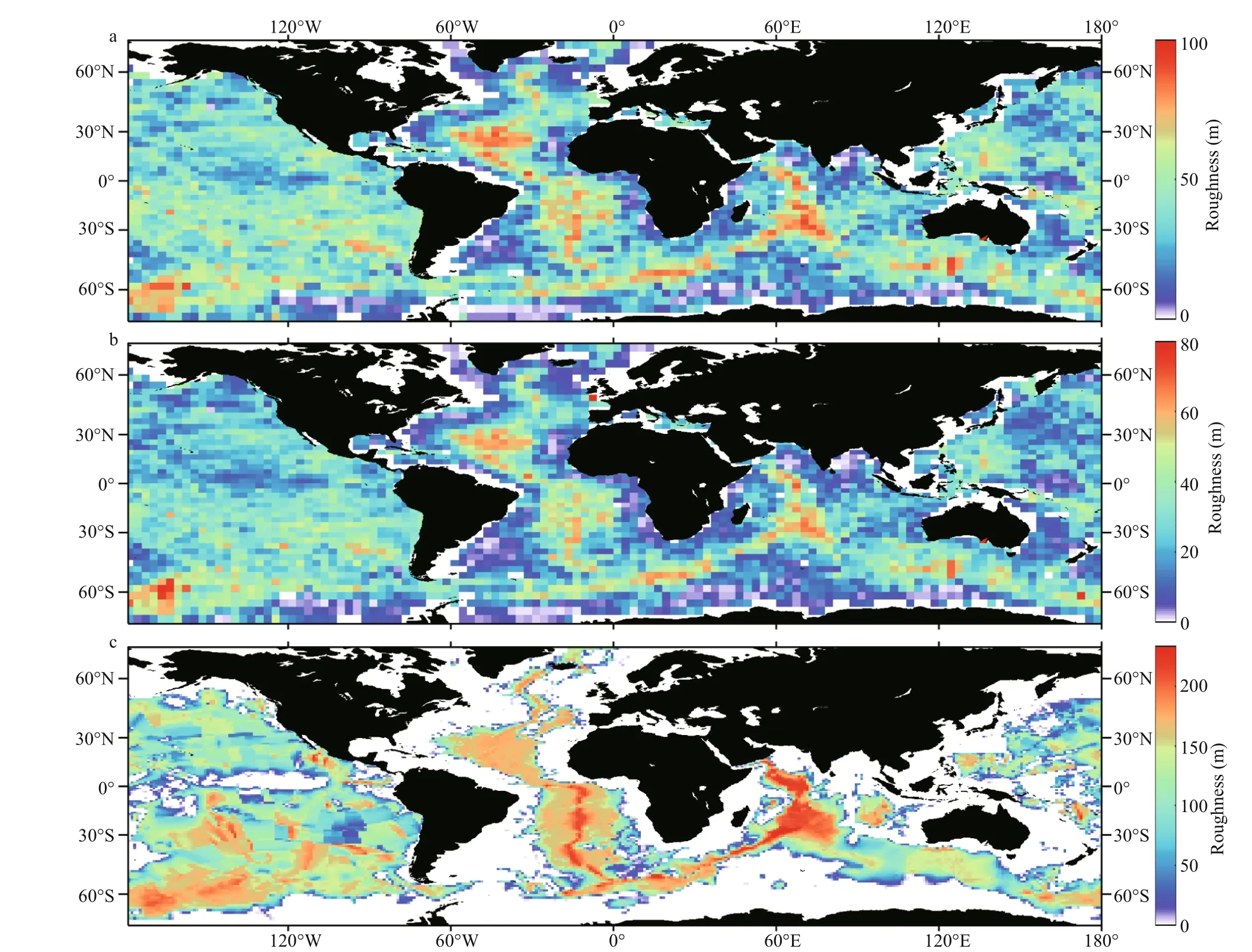
Fig.3 Topographic roughness

To achieve the above goals, the smallest, mean, and largest conversion rate are calculated in the global ocean according to the method that is referred to the Section 2.2. The conversion rate computed by RF has been discussed before, hence the smallest, mean, and largest conversion rate by using RS are focused on in this section. The mean conversion rate has a similar meaning to the conversion rate obtained by RF. The meaning for the largest and smallest conversion rate is that the two values represent the upper and lower global integral energy conversion rates by using linear theory.

The mean conversion rate was compared with the rate obtained by RF. Figure 6b shows that the mean conversion rate is large in the ACC region, equatorial regions, and west boundary currents regions, and is similar to that obtained by RF. The integrated mean energy conversion from the mean flow and eddies in the global ocean are 0.024 and 0.06 TW, respectively(Table 1), which are a little smaller than those obtained by RF. Hence, the data processing procedures can cause inaccuracies in calculating the energyconversion oflee waves in the global ocean.

Table 1 The energy conversion (TW)

The smallest conversion rate from eddies is only large in ACC region and equatorial regions (Fig.6a),because large currents exist in the ACC region and equatorial regions. The conversion rates in the west boundary currents regions are very low, indicating that the topographic spectrum varies largely and the topographic data with high resolution is needed to obtain the accurate conversion rate in these regions.Figure 6c shows that the largest conversion rate shows a similar pattern to that in Fig.6b but the amplitude is larger.

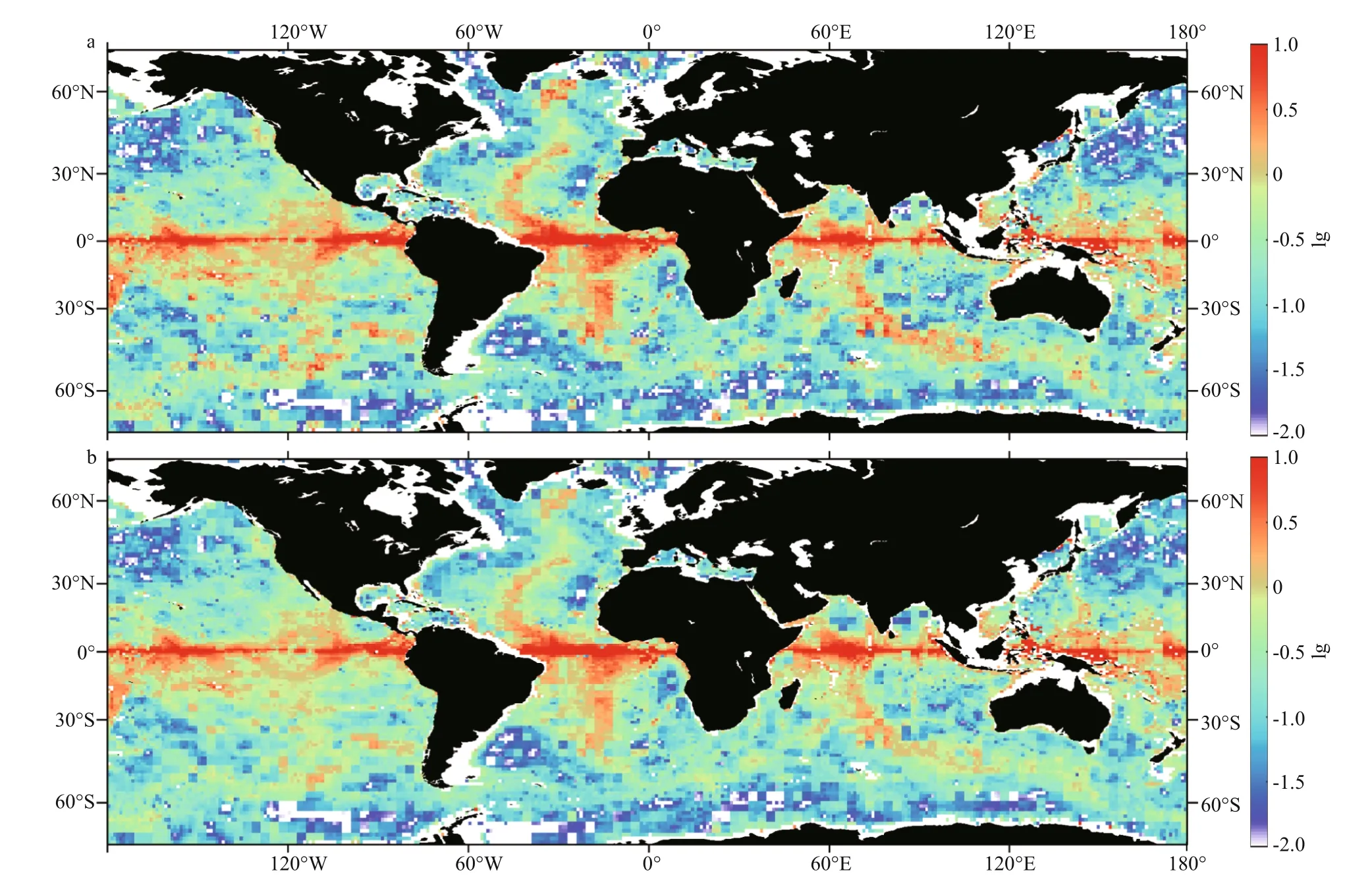
Fig.4 Topographic steepness parameter ε calculated using the mean flow (a) and eddy velocity (b)

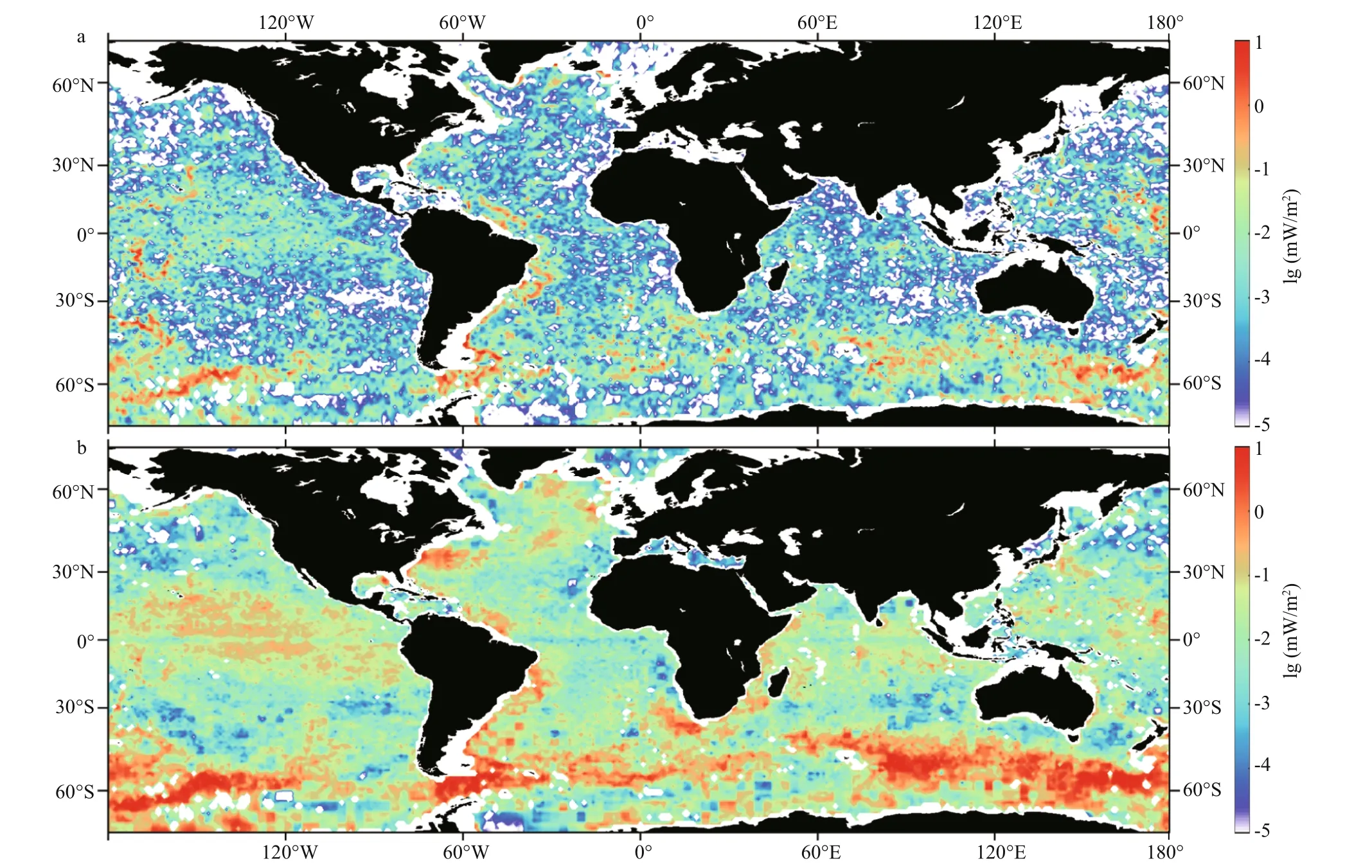
Fig.5 Internal lee wave generation rate calculated from the mean flow (a) and eddies (b)

It would cause errors to calculate the conversion rate in a 3°×3° grid by only using one topographic spectrum instead of using the mean topographic spectra. To better understand the diff erence, the smallest and largest conversion rate from the mean flow and eddies are integrated in the global ocean.The results calculated by diff erent topographic spectra can diff er by almost two orders of magnitude in the global ocean, since the upper energy conversion from the mean flow (eddies) is almost 90 (50) times larger than the lower energy conversion from the mean flow(eddies) (Table 1). Furthermore, the result from eddies only using one topographic spectrum may be 5 times larger or 10 times smaller than the mean value. The results indicate that insuffi cient data resolution can cause inaccuracies on the energy conversion, and the topographic data with high resolution and accuracy is needed to solve the problem. These also indicate that when the resolution of the topographic data is not high or the topographic data are not precise, this may be a factor that causes a large diff erence between the dissipation rate directly obtained from instruments and the energy conversion rate estimated from linear theory.

5 CONCLUSION

In this study, the conversion rate oflee waves from eddies and from the mean flow is computed in the global ocean. The energy conversion from eddies is almost twice as that from the mean flow. The results here stress the importance oflee wave generation from eddies. In addition, the paper explores one possible explanation for the diff erence between the observed dissipation rate and the lee wave generation rate. The results indicate that the topographic spectrum can cause an error of two orders of magnitude in calculating the global energy conversion. In particular,when the resolution of the topographic data is not high or the topographic data are not precise, this may be a factor that causes a large diff erence between the observed dissipation rate and theoretical prediction of energy conversion rate.

The results emphasize the generation oflee waves should be parameterized in eddy-resolving global ocean model. There are some limitations in the research, for example, the mean flow and eddies all come from numerical simulations. To get better results, more observed data are needed. In addition,due to the spatial coverage of the topographic data,the global conversion rate can only be obtained in 3°×3° grids. High resolution of topographic data is needed to improve the results presented in the paper.

6 DATA AVAILABILITY STATEMENT

The spreading rates can be downloaded from https://ngdc.noaa.gov/mgg/ocean_age/ocean_age_2008.html;the sediment thicknessScan be provided at http://www.ngdc.noaa.gov/mgg/sedthick; the WOCE Global Hydrographic Climatology can be downloaded at https://rda.ucar.edu/datasets/ds285.4/#!description; the single beam soundings can be downloaded from https://www.ngdc.noaa.gov/mgg/geodas/trackline.html.