基于连续小波变换和符号传递熵的脑功能网络构建方法

李明爱，张圆圆

（1.北京工业大学信息学部，北京 100124；2.计算智能与智能系统北京市重点实验室，北京 100124；3.教育部数字社区工程研究中心，北京 100124）

1 引言

脑-机接口（Brain-Computer Interface，BCI）技术不依赖于传统的肌肉和神经通路，通过采集到的脑电信号直接解读大脑意识，实现人机或人与周围环境之间的通信［1］.运动想象脑电信号（Motor Imagery ElectroEncephaloGraphy，MI-EEG）是指人在没有执行实际动作的情况下大脑想象肢体运动时产生的脑电信号，其包含了大量的神经生理信息，已被广泛应用于BCI领域［2，3］.人脑是一个复杂而密集的网络，由数十亿相互连接的神经元组成，在执行运动想象任务时，信息始终在不同脑功能区之间相互传递和整合.近年来，基于图论的复杂网络分析方法被广泛应用于神经科学中，通过复杂网络基本原理可以进行大脑属性分析，以及发现脑网络节点间潜在的信息传递关系.越来越多的研究表明，利用脑功能网络（Brain Functional Network，BFN）中的度量来区分运动想象脑电信号具有一定的可行性［4，5］.因此，从BFN 的角度研究不同MI 任务下的大脑活动模式，对揭示运动想象背后的神经机制具有重要的意义.

构建BFN 时，节点通常是EEG 电极，而边定义为节点之间的连接性.计算连接性的指标主要分为两类：功能连接和有效连接.在现有的文献中［6，7］，大多数关于脑功能网络的研究都是基于功能连接度量进行的.Kim等人［8］使用相关系数（Correlation Coefficient，CC）来估计脑网络节点之间的连接性，结果表明，执行左手和右手运动想象任务时，网络节点的CC 值高于脚和舌头，且额叶和顶叶区电极之间的CC 值在也存在显著不同.Gong等人［9］提出一种基于时频交叉互信息（Cross Mutual Information，CMI）的脑功能网络建模方法，研究了四类运动想象任务（左手，右手，脚和舌头）下大脑的生理机制；他们利用统计分析发现不同任务下大脑的反应水平、反应时间和激活靶区都存在明显的差异.Filho等人［10］提出一种基于图案同步法（Motifs'Synchronization，MS）的脑功能网络构建方法，针对BCI2000 数据集中十名受试者的左手和右手MI-EEG进行模式识别.结果显示，在α频带和β频带上，平均分类准确率均达到了83%.然而，功能连接度量仅能捕获电极之间在统计意义上的相互依赖性，却无法提供信息流动的方向以及不同神经结构之间的因果关系.

有效连接可描述节点之间的因果交互作用，相比于功能连接，它能更容易发现运动想象过程中节点之间隐藏和被忽视的连接性.Hu 等人［11］使用基于时不变双变量自回归（Bivariate Autoregressive，BVAR）模型的格兰杰因果指数（Granger Causality，GC）研究了运动想象任务的大脑因果信息流.他们发现在左手和右手运动想象期间，Cz导联与C3/C4之间的方向性连接有很大不同.Ghosh 等人［12］提出一种基于多元自回归模型（MultiVariate AutoRegressive，MVAR）定向转移函数（Directed Transfer Function，DTF）的BFN 构建方法，实验结果表明，利用网络节点度和网络密度可有效区分左手、右手和舌头的MI-EEG 信号.不足的是，GC 和DTF 依赖于线性自回归模型，使得它们难以准确地反映出人脑这种高度非线性系统中存在的因果关系.

传递熵（Transfer Entropy，TE）是一种基于非参数统计的信息理论量，它不需要预先假设交互作用的模型，可用于衡量两个非线性向量之间信息交互，是研究大脑信息流的理想方法［13］.符号传递熵（Symbolic TE，STE）是传递熵的一种变体，具有计算速度快，抗噪声能力强等优点［14］.已有研究人员将其应用于脑功能网络的构建中，并根据不同MI 任务下节点间连接性的差异来区分运动想象脑电信号［15］.然而，现有方法直接通过计算原始MI-EEG 之间的连接性来构建BFN，难以充分利用脑电信号在频域上的特征信息.

为此，本文提出了一种基于连续小波变换（Continuous Wavelet Transform，CWT）和STE 的脑功能网络构建方法，将EEG 电极的时频能量序列作为网络节点的输入信号，并使用符号传递熵计算脑电极之间的非线性因果交互作用.在BCI 2000 公开数据集上进行了实验研究，以验证本文方法的有效性和优越性.

2 方法

本文提出了一种基于连续小波变换和符号传递熵的脑功能网络建模方法，其主要步骤如下：

2.1 基于CWT获取EEG的时频能量序列

2.1.1 连续小波变换

连续小波变换通过小波函数的伸缩和平移将信号分解成不同尺度上的小波系数，已被广泛应用于信号的时频分析和处理领域［16］.对于任意能量有限信号s(t)，其连续小波变换的公式为

式中，WΤ 为小波系数，a为尺度因子，b为平移量，ψ(t)为母小波函数，ψa，b(t)为伸缩平移后的小波函数，ψ*(t)为ψ(t)的共轭复数.

2.1.2 获取MI-EEG的时频能量序列

2.2 基于符号传递熵构建脑功能网络

2.2.1 序列符号化

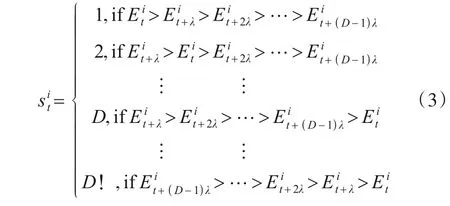
图1 序列符号化示意图

2.2.2 符号传递熵

符号传递熵根据符号序列中各符号出现的相对频率来估计联合概率分布和条件概率分布.对于两个符号序列，它们之间的符号传递熵可通过下式计算：

式中，p(·)为概率密度函数，τ为时间滞后.

2.2.3 构建脑功能网络

以L个EEG 电极为节点，将任意两导脑电信号时频能量序列之间的符号传递熵作为连接边，计算脑功能网络的连接矩阵A：

3 实验研究

为了验证本文方法的有效性，本文分析了不同运动想象任务的脑功能网络，并分别以连接矩阵元素和脑网络特征参数作为分类器的输入，对MI-EEG 信号进行模式分类.

3.1 实验数据及预处理

实验使用的MI-EEG 数据来自于BCI 2000 公开数据库［17］，共记录了64个头皮电极的脑电数据，电极分布位置如图2 所示.采集的EEG 经过1 Hz～50 Hz 带通滤波及50 Hz 陷波滤波，采样频率为160 Hz.该数据库共包含109 名受试者，每名受试者进行约45 次实验，想象任务为左手或右手运动，每次实验持续约8 s，其中0 s～4 s为运动想象期.

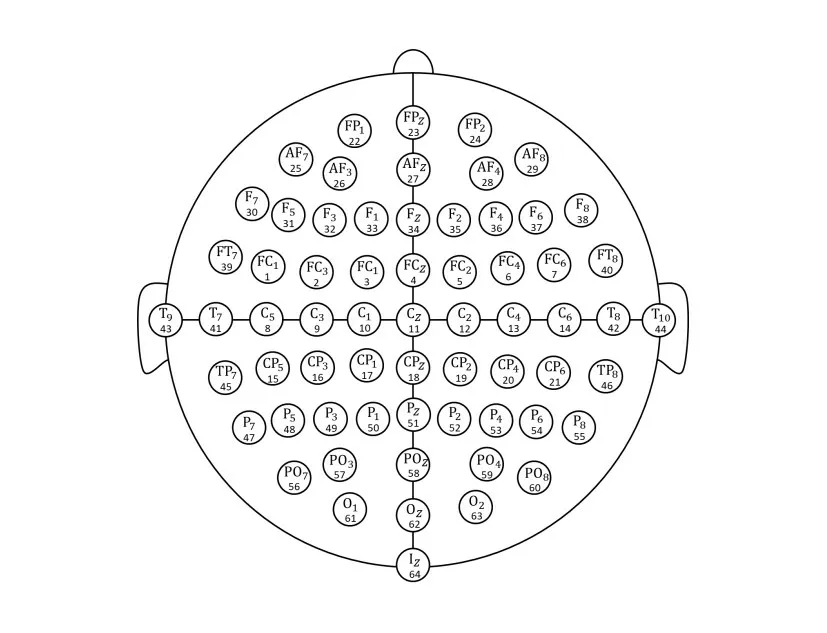
图2 电极位置与导联序号分布图

构建BFN 的一个关键挑战是体积传导效应，它会导致头皮电极之间产生虚假连接性，从而误导对脑网络的分析.共平均参考（Common Average Reference，CAR）使用所有导联的平均值对信号进行重定位，可有效减小体积传导效应［18］.因此，本文在预处理阶段截取了0 s～4 s想象期的MI-EEG数据，并使用CAR滤波器对其进行空间滤波.

3.2 基于连接矩阵的MI-EEG识别

3.2.1 计算有效连接矩阵

根据2.1 节，使用连续小波变换对预处理后的脑电信号进行时频分解，图3 为基于Morlet 连续小波变换对某次实验C3 导联MI-EEG 信号进行分解后得到的时频能量图，横轴为时间，纵轴为频率，颜色代表小波能量值.在执行运动想象任务时，事件相关去同步（Event-Related Desynchronizations，ERD）/事件相关同步（Event-Related Synchronizations，ERS）现象大多出现在Mu节律（8 Hz～13 Hz）和Beta节律（13 Hz～30 Hz）上［19］.因此，本文分别截取了时频能量图的α（8 Hz～13 Hz）和β（13 Hz～30 Hz）两个频带进行分析.以β频带为例，小波分解后β频带范围覆盖12 个离散频率，记为：f1，f2，…，f12，将其对应的时间-能量序列依次拼接后得到一维时频能量序列，如图4所示.

图3 C3导联MI-EEG的时频能量图

图4 C3导联β频带的一维时频能量序列

以64 个EEG 电极作为脑网络的节点，计算任意两个电极时频能量序列之间的符号传递熵（实验中λ和τ均设为1），得到64×64 的有效连接矩阵.图5 展示了受试者S1的连接矩阵图，其横轴与纵轴均表示导联序号，且导联与电极之间的一一对应关系与图2中一致，矩阵中的元素代表两个导联之间的因果连接性.由图可见，大脑在进行想象左手运动和想象右手运动两类任务时，节点之间的连接性具有显著不同，图中紫色圆圈标记了两类想象任务连接性显著不同的部位.当想象左手运动时，位于中央脑区右侧的C4 节点与位于前额右侧的节点（FC2、FC4、FC6）之间的连接性远大于想象右手运动；而想象右手运动时，信息由顶叶右半区传递至前额叶左半区，位于顶叶右侧的节点（如P2、P4）与前额叶左侧的FP1 节点之间的连接性明显强于想象左手运动.

图5 受试者S1两类想象任务的大脑连接矩阵图

3.2.2 特征选择和分类

大脑进行运动想象时，并非所有区域都会被激活，使用连接矩阵中的全部元素作为特征可能不利于MIEEG的识别.因此，有必要对矩阵进行优化.

对于每名受试者，本文通过计算大脑连接矩阵各位置元素与类别标签之间的皮尔逊（Pearson）相关系数值来优化矩阵元素，将相关性较小的元素置零，保留相关性较大的元素.提取优化后矩阵的非零元素构成特征向量，采用支持向量机（Support Vector Machine，SVM）分类器进行模式分类，并借助网格搜索法确定SVM 分类器的最优超参数［20］.由于每名受试者的实验次数较少，本文使用留一法对样本进行测试，即每次分类使用一次实验的MI-EEG数据作为测试集，剩余44次实验数据作为训练集，最终结果取45 次分类结果的平均值.

图6 显示了受试者S1 的分类准确率随皮尔逊相关系数阈值的变化情况.由图知，阈值的选择对分类准确率有着较大的影响，当阈值小于等于0.30 时，分类准确率逐渐升高；而当阈值大于0.30 时，分类准确率则出现了明显下降；当阈值设为0.30 时，分类准确率达到了最大值100.00%，从而确定S1 的最优皮尔逊相关系数阈值为0.30.依此方法，确定其他每名受试者的最优Pearson相关系数阈值.

图6 受试者S1的分类准确率

此外，本文还对比了Wrapper 和Fisher 滤波这两种不同特征选择算法的分类准确率，结果如表1所示，表中准确率为109名受试者的平均值.从表1中可以看出，当不使用特征选择算法时（表中None），分类效果较不理想，平均准确率仅为63.95%；而使用特征选择算法优化矩阵元素后，分类准确率有了大幅度的提升，且三种特征选择算法的准确率相近.使用Pearson 特征选择算法的准确率最高，达到了94.75%，而使用Wrapper 时的准确率为94.46%，使用Fisher滤波时结果为94.74%.这说明使用有效连接矩阵中的全部元素构建特征向量，会造成特征信息的冗余，并不利于MI-EEG的分类.

表1 还给出了不同特征选择算法在达到平均分类正确率时所需要的特征数目，可以看出，当使用Pearson特征选择算法时，所需特征数目最少，仅为120个，相比于未进行矩阵优化时的4 096 个特征，极大地降低了分类的计算成本.

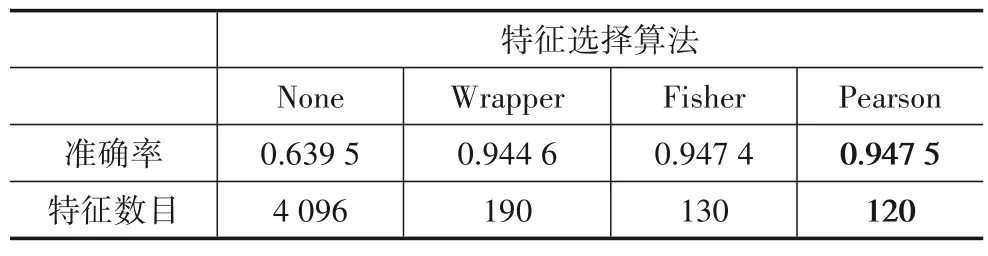
表1 不同特征选择方法的平均准确率对比

3.2.3 选取母小波函数

与传统脑网络构建方法不同，本文首先基于CWT求取信号的时频能量序列，然后将电极时频能量序列之间的符号传递熵作为网络的边，进一步提取了EEG信号的时频特征.为了选择最适合表达MI-EEG信号时频信息的母小波函数，本节将针对不同母小波函数的分类结果展开讨论.

实验选取了五种经典的母小波函数进行对比研究，分别为：Haar 小波、Daubechies 小波、Mexican Hat 小波、Meyer小波和Morlet小波.表2同时给出了基于不同小波函数获得的109 名受试者的平均分类准确率以及单个受试者的最高准确率，表中的None 则表示未对EEG 信号进行连续小波变换，仅将各通道EEG 信号之间的符号传递熵作为网络连接边时的识别正确率.

表2 不同小波函数的分类准确率

从表中可以看出，不同频带下的分类准确率略有差异，且β频带的正确率均高于α频带，这可能是由于受试者在进行左手、右手运动想象时，β频带的ERD/ERS 生理现象更加明显.同时，无论是在α频带还是β频带，当以原始EEG 信号之间的符号传递熵为边构建脑功能网络时，得到的平均分类准确率是最低的，这是由于原始脑电信号难以体现MI-EEG 在频域上差异，而连续小波变换通过在时间和频率两个尺度上对信号进行分解，可以较好地提取信号在频域上的特征，进而为正确识别脑电信号提供了更多的有用信息.此外，Daubechies、Meyer 和Morlet 三个小波函数在两个频带下单个受试者的最高分类准确率均为100.00%，但Morlet 小波的平均分类正确率最高，在α频带达到了90.78%，在β频带为94.75%；这表明，相比于其他四个母小波函数，Morlet 小波函数能够更好地表达出MIEEG 的时频特性，并且对于不同受试者能表现出较好的鲁棒性.因此，基于Morlet 小波函数的连续小波变换将用于本文后续的实验中.

3.2.4 确定最优符号阶次

计算两个信号之间的符号传递熵的第一步是对信号进行符号化，为了不丢失EEG 信号的时间信息，实验应确保每个符号都尽可能地出现在信号中.根据文献［21］，对于长度为Nt的信号，符号阶次D应满足Nt＞＞D！.因此，本文选取D=2，…，6 进行了对比研究，实验结果如图7 所示，图中准确率为109 名受试者的平均分类准确率.总体来看，无论是α频带还是β频带，随着符号阶次的增加，分类准确率先升高后降低.除此之外，β频带的正确率仍然高于α频带，这一结果与3.2.3 节类似；当D=2 时，分类准确率最低，为87.97%；D=4 时，准确率达到了最大值94.75%；而当D继续增大时，正确率则发生了下降，这可能是由于D=4 时最能吻合该数据集脑电信号的复杂性.

3.3 基于网络拓扑特征参数的MI-EEG分类

3.3.1 计算脑网络特征参数

为了进一步研究在不同运动想象任务下大脑各区域的激活模式，本文计算了两个重要的脑网络参数：度和中间中心性.由于二值化有效连接矩阵可能会丢失部分重要的网络信息，本文使用文献［22］中的方法计算加权网络的特征参数：

（1）度（Degree）

节点度的计算式如下：

式中，aij为节点i和节点j之间的连接性，节点的度越大，表明该节点与其他节点之间的连接性就越强.

（2）中间中心性（Betweenness Centrality，BC）节点i的中间中心性可由式（7）计算：

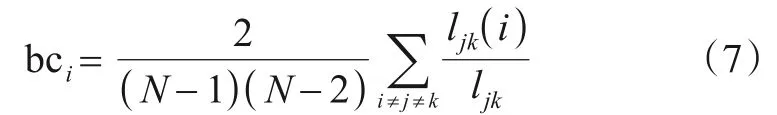
依据式（6），计算所有节点的度，构成特征向量FD：

由式（7），计算每个节点的中间中心性，构成特征向量FBC：

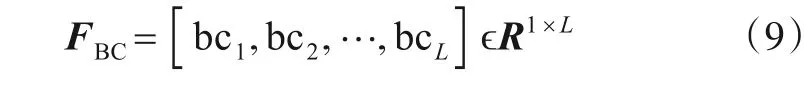
将FD与FBC串行融合，获得融合特征向量FD+BC：

为了体现脑功能网络的时变特性，本节采用窗长为2 s，步长为1 s 的滑动时间窗将原始数据划分为T1(0 s～2 s)、T2(1 s～3 s) 和T3(2 s～4 s)三个时间段，每个时间段数据共包含320 个采样点.对每个时间段信号分别构建脑功能网络，并计算特征向量.

3.3.2 基于网络特征参数的MI-EEG分类

图8（a）展示了在不同时间段内，想象左手运动和想象右手运动的脑地形图，使用的特征参数为度.可以看出，随着时间的变化，大脑的激活区域呈现一定的变化规律，但总体来看，执行左手运动想象任务时，位于右侧脑皮层的节点强度更大，而执行右手运动想象时，位于大脑左侧区域的节点度更高.图8（b）为使用中间中心性作为特征参数时的脑地形图，对比于图8（a），本文也能得到类似的结果.这从复杂网络的角度进一步阐述了ERD/ERS 现象在运动想象任务中的模式，即大脑在执行手部运动想象任务时，对侧脑功能区更有可能被激活.

图8 不同时间段的脑地形图

此外，本文还尝试以度和中间中心性来构建特征向量对两类MI-EEG进行模式分类.同样使用Pearson特征选择算法优选贡献度较大的特征.图9展示了β频带下D=4时T1、T2和T3三个时间段的分类准确率及平均分类准确率.可以看出，仅使用BC值作为特征时，三个时间段的平均准确率为86.20%；仅使用Degree 时，三个时间段的平均准确率为89.83%；将Degree与BC融合时，平均准确率为92.38%.特别地，在T2时段，使用BC和Degree融合特征时，分类准确率达到了93.55%，这一结果接近于使用连接矩阵元素作为特征时的准确率94.75%.此外，图10还给出了达到图9分类准确率时所需的特征数目.可见，当使用网络特征参数进行分类时，达到最优准确率所需的特征数目仅为32，这相比于使用连接矩阵元素aij作为特征时的数目减少了约3/4.

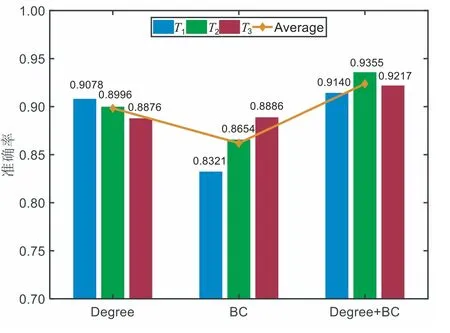
图9 不同时间段的分类准确率

图10 获得图9准确率所需的特征数目

3.3.3 多种脑网络特征提取方法对比

为了验证本文提出的脑功能网络构建方法的优越性，本节还对比了不同方法在该数据集下的分类性能，结果如表3所示，表中分别计算了将有效连接矩阵元素aij以及脑网络参数Degree+BC 作为分类器输入时109名受试者的平均分类准确率和Kappa 值.从表中可以看出，互信息（CMI）和相关系数（CC）的分类准确率较低，这是由于它们无法衡量EEG 电极之间连接的方向性，造成特征信息的丢失；而格兰杰因果指数（GC）和定向传递函数（DTF）能够表示信号之间的因果连接性，这种连接性是具有方向的，从而为脑电信号的识别提供了更多的有用信息.不足的是，GC 和DTF 是基于线性回归模型估计的，将其应用于人脑这样的非线性动力系统中难免会存在一定的局限性.相比之下，符号传递熵更适合反映脑电极之间的交互作用，且这种交互作用是有向的、非线性的，符合人脑的非线性动力学特性，因此取得了最高的分类准确率和Kappa 分数.本文还对比了文献［10］中使用图案同步法（MS）在相同数据集下的分类结果，当以连接矩阵元素aij为特征时，平均分类准确率提升了11.59%；当以Degree 和BC 为特征时，准确率提高了11.41%，显示了本文方法的有效性和优越性.

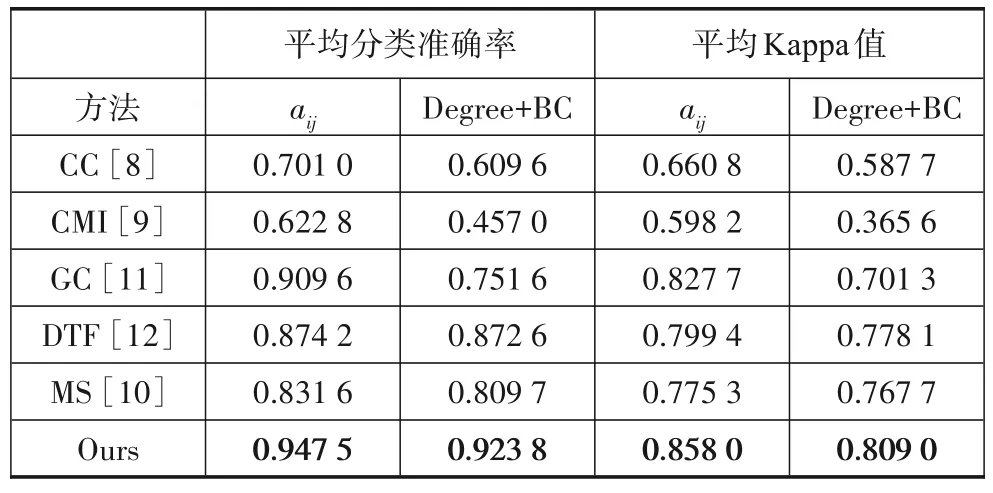
表3 基于多种脑功能网络方法的109名受试者平均分类准确率和Kappa值对比

4 结论

本文提出了一种基于CWT 和STE 的脑功能网络建模方法，克服了传统脑网络构建方法易丢失脑电信号的频域信息这一不足，并能够准确地反映不同节点之间的非线性因果交互作用.在BCI 2000 公开数据集上的实验结果表明，虽然不同运动想象任务的BFN 具有一定差异性，但大脑对MI 任务的反应是局部的.当使用网络连接矩阵的全部元素作为特征时，分类效果并不理想，而合理使用特征选择算法可以较大幅度地提高识别正确率；此外，本文发现在执行手部运动想象任务时，位于大脑对侧功能区节点的Degree 和BC 值大于同侧，这从复杂网络的角度进一步阐述了在进行运动想象时大脑的ERD/ERS 生理现象；同时，本文还尝试了以网络特征参数Degree 和BC 为特征对MI-EEG 信号进行识别，获得的分类准确率十分接近于直接使用aij时的结果，而特征向量的长度更小，这减少了分类的计算成本.最后，对比了多种脑功能网络构建方法的分类性能，本文方法均获得了最高的平均分类准确率和Kappa值，这说明本方法能有效地体现运动想象脑电信号的时频特征和非线性特征，相比于其他方法具有显著优势.这一改进有助于脑科学的研究，并将扩大脑网络分析方法在EEG中的应用.

在未来的工作中，我们将进一步筛选合适的脑网络拓扑特征参数，深入研究运动想象过程中大脑的神经生理机制以及脑网络的动态变化规律；同时尝试将脑功能网络分析方法与其他方法相结合进行多元特征提取，以进一步提高BCI 系统中MI-EEG 的识别正确率.