逻辑演算方法在点集问题中的应用
徐斌
(普洱学院 数学与统计学院,云南 普洱 665099)
1 引言及预备知识
度量空间中关于点集的问题[1-2](导集、边界、内部等)是比较精细及抽象的,其在实变函数课程中具有重要的地位.传统的定义及处理方式往往是用汉字语言加数学符号来描述及推理[3-8],由于汉字语言不能直接参与“演算”,使得这些关于点集的问题(运算、关系等)处理起来非常困难,初学者普遍感到晦涩难懂.经过多年的教学研究与实践,发现如果采用一阶量词逻辑[9-10]语言来等价地描述相关概念,再借助量词逻辑的推理演算方法,就可以清晰而简便地处理此类问题,使得学习难度大为降低.因此,本文将论述及演示用一阶量词逻辑演算处理度量空间中点集问题的方法.
设p是一个确定的条件,所谓条件是指对于任意的个体x,“x满足条件p”与“x不满足条件p”两者必定有且只有一条成立.个体变元用x表示,取定的个体常元用x0表示,称p(x0),∃x(p(x)),∀x(p(x))为原子命题,其定义分别是:(1)p(x0),记作A=p(x0),若个体x0满足条件p,则称A为真命题;若个体x0不满足条件p,则称A为假命题.(2)∃x(p(x)),记作A=∃x(p(x)),若存在个体x0满足条件p,则称A为真命题;若对于任意一个个体x,x都不能满足条件p,则称A为假命题.(3)∀x(p(x)),记作A=∀x(p(x)),若对于任意一个个体x,x都可以满足条件p,则称A为真命题,若存在个体x0不满足条件p,则称A为假命题.
设A,B是原子命题,则称AˆB,AˇB,A→B,┑A,A↔B为命题,其定义分别是:(1)AˆB,称为A,B的合取命题,记作C=AˆB,当且仅当A,B都为真命题时C为真命题,其余情况C为假命题.(2)AˇB,称为A,B的析取命题,记作C=AˇB,当且仅当A,B都为假命题时C为假命题,其余情况C为真命题.(3)A→B,称为A,B的蕴含式命题,记作C=A→B,当且仅当A为真命题且B为假命题时C为假命题,其余情况C为真命题.(4)┑A,称为A的否命题,记作C=┑A,若A为真命题,则C为假命题;若A为假命题,则C为真命题.(5)A↔B,称为A,B的等价式命题,记作C=A↔B,则C=(A→B)ˆ(B→A).
本文所说的一阶量词逻辑公式是指由AˆB,AˇB,A→B,┑A,A↔B5 种命题运算经过有限次复合代入所生成的式子.设A,B都是命题,若A↔B是真命题,则称A,B等价,记作A⇔B,在一阶量词逻辑公式中等价的命题可以相互替换,即若A⇔B,则φ(A)⇔φ(B);若A→B是真命题,则称命题A可以推出命题B,记作A⇒B,平时所用的许多不同的推理模式都是从这种恒真蕴含式获得的.
给出一些常用的运算及等价代换与推理的公式:
(1)关于一般命题的公式,设A,B,C都是命题,则有(AˆB)ˆC⇔Aˆ(BˆC),(AˇB)ˇC⇔Aˇ(BˇC),AˆB⇔BˆA,AˇB⇔BˇA,Aˆ(BˇC)⇔ (AˆB)ˇ(AˆC),Aˇ(BˆC)⇔ (AˇB)ˆ(AˇC),┑(AˆB)⇔ (┑A)ˇ(┑B),┑(AˇB)⇔ (┑A)ˆ(┑B),A→B⇔ (┑A)ˇB,┑(┑A)⇔A.
(2)关于量词的公式,主要有:∀x∊Ω(p(x))⇔∀x(x∊Ω →p(x));∃x∊Ω(p(x))⇔∃x(x∊Ω ˆp(x));┑(∀x(p(x)))⇔∃x(┑(p(x)));┑(∃x(p(x)))⇔∀x(┑(p(x)));∀x∀y(p(x,y))⇔∀y∀x(p(x,y));∃x∃y(p(x,y))⇔∃y∃x(p(x,y));∀x(p(x)ˆq(x))⇔∀x(p(x))ˆ∀x(q(x));∃x(p(x)ˇq(x))⇔∃x(p(x))ˇ∃x(q(x));∃x(p(x)ˆq(x))⇒∃x(p(x))ˆ∃x(q(x));∀x(p(x))ˇ∀x(q(x))⇒∀x(p(x)ˇq(x));∃x∀y(p(x,y))⇒∀y∃x(p(x,y)).
2 方法及路径
用一阶量词逻辑演算方法处理度量空间中的点集问题,首先要将这些点集的传统定义等价地翻译成一阶量词逻辑公式,然后借助一阶量词逻辑演算及一些等价转化的方法来实现演算推理.
2.1 相关概念的逻辑描述
度量空间(R,d)的度量为d,集合称为以x0为心δ为半径的邻域,记作U δ(x0);集合称为以x0为心δ为半径的去心邻域,记作设E为实数集R中的一个给定点集,x0是R中的一个点,则
(1)x0是点集E的聚点,E的所有聚点组成的集合称为E的导集,记作E′.
(2)x0是点集E的内点⇔∃δ>0(Uδ(x0)⊆E),E的所有内点组成的集合称为E的内部,记作.
(3)x0是点集E的外点⇔∃δ>0(Uδ(x0)∩E=Ø),E的所有外点组成的集合称为E的外部,记作Ee.
(4)x0是点集E的界点,E的所有界点组成的集合称为E的边界,记作∂E.
(5)x0是点集E的触点⇔∀δ>0(Uδ(x0)∩E≠Ø),E的所有触点组成的集合称为E的闭包,记作.
(6)x0是点集E的孤立点⇔x0∊E-E′.
2.2 等价转化的方法与路径
等价转化主要包括集合与条件的转化、集合运算式与集合关系式的转化、集合关系式与逻辑公式之间的转化.集合与条件的转化遵循基本原理1.
基本原理1.
设A是集合,且,则x∊A⇔p(x).
设A,B是集合,利用A=B⇔A⊆BˆB⊆A,A∩B=A⇔A⊆B,A∪B=A⇔B⊆A,A∩B=Ø ⇔A⊆Bc,A∪B=Ø ⇔A=B=Ø等可以实现集合运算式与集合关系式之间的转化.
集合关系式与逻辑公式之间的转化主要遵循2个基本原理:
基本原理2A⊆B⇔∀x(x∊A→x∊B).
基本原理3A=Ø ⇔∀x(x∉A).
设A,B是集合,且.由基本原理2可知,要证明A⊆B等价于要证明∀x(q1(x)→q2(x));进一步,若要证明A=B,等价于要证明∀x(q1(x)↔q2(x)).这样的过程实现了集合关系式与逻辑公式之间的相互转化.
3 几个常用重要公式的逻辑演算证明
命题1对于度量空间中的点集E,有
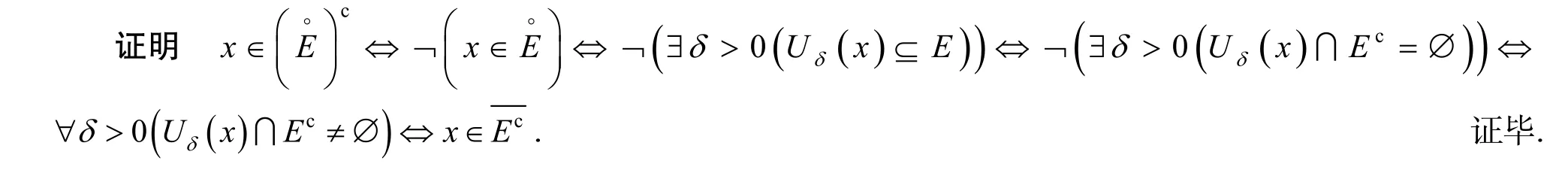
命题2对于度量空间中的点集E,有E′⊆E′.
证明显然E′⊆E′⇔∀x(x∉E′→x∉E′).由于
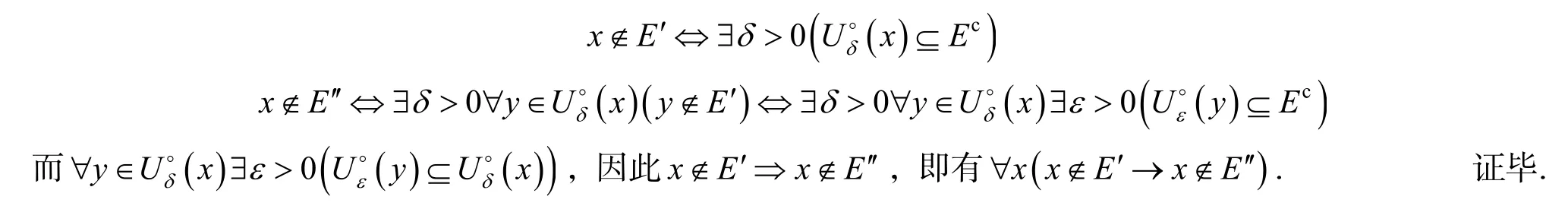
命题3对于度量空间中的点集A,B,有(A∪B)′=A′∪B′.

命题4对于度量空间中的点集A,B,有(A∩B)′⊆A′∩B′.
证明显然(A∩B)′⊆A′∩B′⇔∀x(x∉A′∩B′→x∉(A∩B)′).由于

命题5A×B为度量空间中点集A,B的笛卡尔积,则有
证明由闭包的定义可知,原命题等价于(A×B)′=(A′×B)∪(A×B′)∪(A′×B′).

4 结语
研究发现,导集运算是最为基本的集合运算,其他运算都可以借助求导及交、并、差等初等运算得以定义.故而,只要掌握了关于导集运算的基本性质就可以推导出其余4个运算所具有的性质与规律.
实践表明,利用一阶量词逻辑演算的方法来证明这些抽象精细的命题是清晰而简便的.进一步地,还可以仿照以上方法简便地证明常用公式:

