卷积式的拓方运算及其应用

刘智全

（唐山市丰润镇中学，河北 唐山 064000）

1 引言及预备知识

在文献[1]给出的卷积式基础上，提出了卷积式的拓方运算，研究了其运算性质，进而提出了高次组合数及相关公式.运用该运算及一些数学方法和技术[2-9]，解决了若干个多项式积的展开问题及2 类Stirling数的卷积式表示问题.文中相关符号含义见文献[1-2].

m×(n+1)型卷积式指的是项的和，这些项取自其中的不同行，每一项的形式为a1j1a2j2…amjm，且j1+j2+…jm=n.

定义（卷积式的拓方）用符号表示卷积式的r（r为整数）次拓方，其满足条件：

（1）当r≤1 时，，并且约定当r＜ 1-n时，A的r次拓方恒为零.

（2）当r＞1 时，

由卷积式拓方的定义可知，某卷积式的一次拓方是原卷积式本身，卷积式拓方后仍是一个卷积式，卷积式的性质在其拓方中均成立.

2 卷积式拓方的运算性质

定理1

证明由卷积式拓方的定义，有

由定理1 可得到定理2.

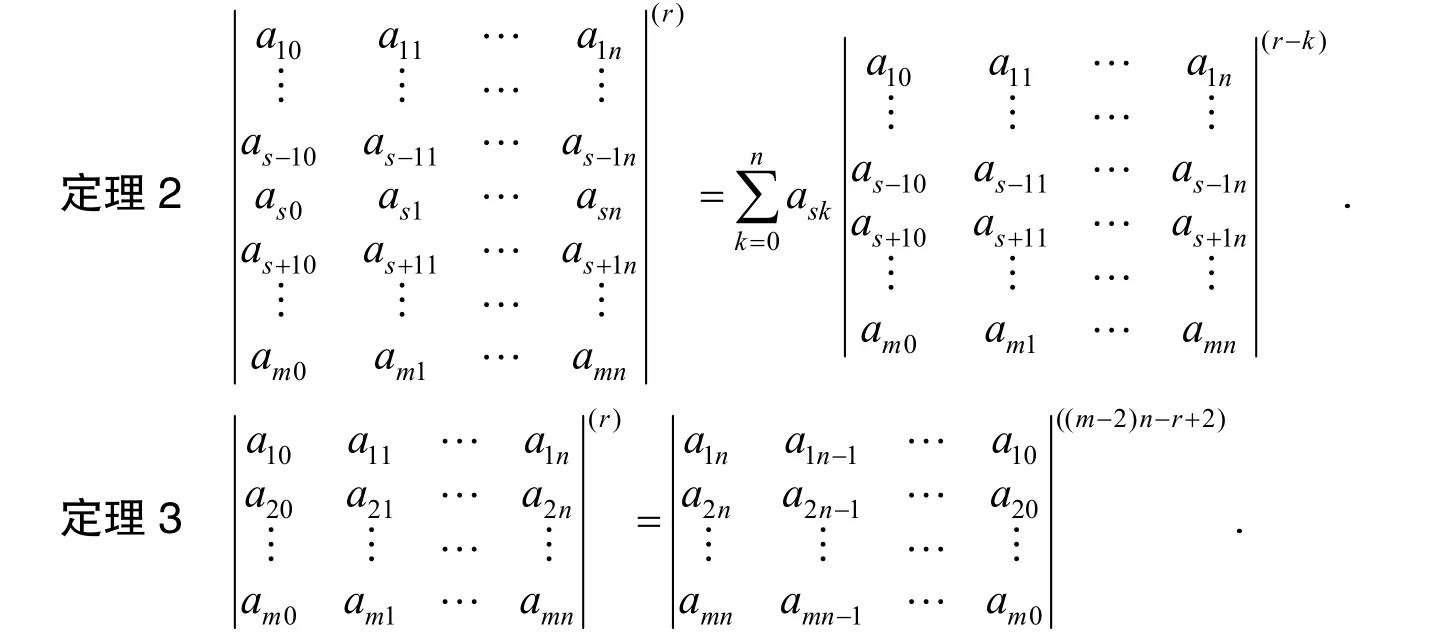
证明对行数m作数学归纳法.容易验证，m=1,2时命题成立.假设m=k时命题成立，即

当m=k+1时，由定理2 及归纳假设可知，，即m=k+1时命题成立.

定理4当r＞ (m-1)n+1时，

使用归纳法可证明定理4.由定理3～4 易见卷积式拓方定义中的约定是合理的.

当n=1 时，的一个特例.

由卷积式及其拓方的定义不难得到定理5.

定理5卷积式A的r次拓方是项的和，这些项是取自A的不同行的m个元素的乘积，每一项的形式为a1j1a2j2…amjm，j1+j2+…jm=n+r-1.

3 卷积式及其拓方的应用

3.1 若干个多项式的乘积

文献[1]中应用卷积式成功解决了若干个幂级数的乘积展开问题，在此基础上再应用卷积式及其拓方的有关知识不难得到关于若干多项式积展开问题的相关定理.

应用定理6 可将任意的几个多项式的积直接展开成一个新的多项式.

例求的展开式.

解由定理6 可知，

3.2 2类Stirling 数的卷积式表示

令t表示任意实数，则阶乘函数的定义为(t)0=1,(t)n=t(t-1)…(t-n+1)(n≥1).分别用s1(n,k),s2(n,k)表示第一类Stirling 数和第二类Stirling 数，它们满足：(t)0=(t)0=s1(0,0)=s2(0,0)=1，

利用卷积式的有关理论及其相关结果可将2类Stirling 数分别用不同形式的卷积式表示出来.

引理1

证明当n≥m-1时，有

应用卷积式相关性质、计算定理，按照上述方法一直做下去，就可以得到

同样地，应用卷积式的相关计算定理不难计算出当n＜m-1时，卷积式的值为零. 证毕.

由定理5 可得到引理2.

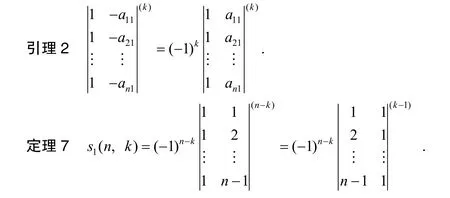
证明由第一类Stirling 数的定义，依次运用定理6、定理3 和引理2 可知，将此式与比较可知，.证毕.

定理8（卷积式的行数为k）.

证明因为，，由引理1可知，，又因为证毕.