一类复积分错误计算的分析
张杰华,韩明华
(凯里学院 理学院,贵州 凯里 556000)
1 引言及预备知识
复积分的计算是复变函数与积分变换课程的一个重要内容,计算的方法多样,其中利用留数定理可以方便地解决一类沿封闭曲线的积分.当被积函数是分式时,大量的文献讨论了这种情形下积分的计算方法和性质[1-3].留数定理能够解决许多复杂的积分计算问题,文献[4-6]讨论了留数定理及其应用.本文以一道典型的习题为例讨论复积分的计算问题.
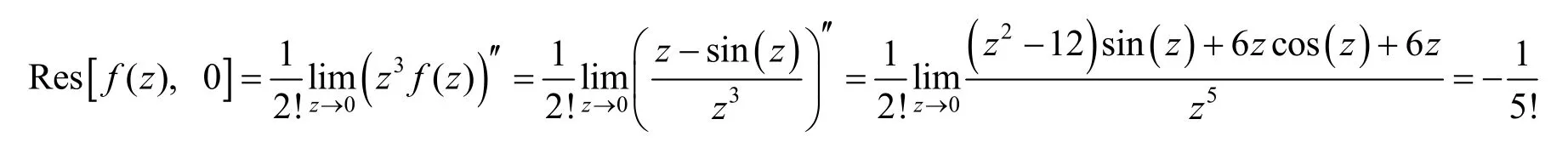
部分学生判别奇点的时候出现了错误,看见分母是z6而误认为z=0 是f(z) 的6 阶极点,计算结果为
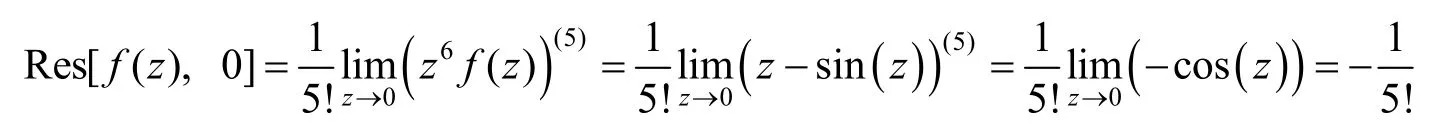
在判别极点阶数时出现了错误,但是最后的计算结果竟然是正确的,而且计算过程相比较正确方法还要简单,出现这种情况是否是一种巧合,本文对这个问题进行了探讨.
定义[9]设z0为解析函数f(z) 的孤立奇点,f(z) 在z0处的洛朗展开式中负一次幂项的系数C-1被称为f(z)在z0处的留数,记为Res [f(z),z0].
留数定理[10]216设函数f(z) 在区域D内除有限个孤立奇点1,2,,nz z…z外处处解析,C是D内包围各奇点的一条正向简单闭曲线,则有
引理[10]224如果z0为f(z) 的m阶极点,则
2 主要结果及证明
定理若f(z)在简单闭曲线C所围成的区域D内至多存在孤立奇点z0,而在上连续,则有
(1)若f(z) 在区域D内解析或者z0是f(z) 的可去奇点,则
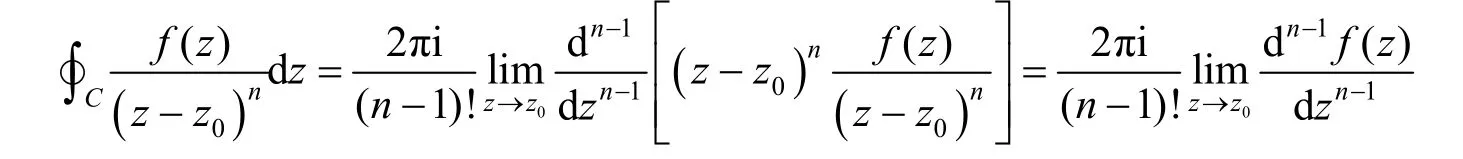
(2)若z0是f(z) 的极点或本性奇点,则
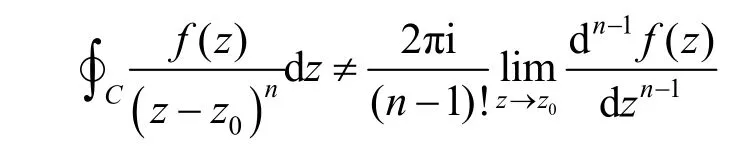
证明(1)假设f(z)在简单闭曲线C所围成的区域D内解析,在D=D∪C上连续.若z0是f(z)的k阶零点,则有f(z0)=0,f′(z0)=0,…,f(k-1)(z0)=0且f(k)(z0) ≠ 0,f(z)也可表示为f(z)=(z-z0)kφ(z),式中:φ(z0)≠ 0.


当z0是f(z) 的可去奇点时,证明方法类似.

分析所围成的区域内存在一个可去奇点z=1,并且z=1 是f(z) 的二级零点,从而z=1 是的一级极点.如果利用引理来计算留数,求解导数及极限的过程会比较繁琐.根据定理的第1种情形来计算积分,可以简化计算过程.
解利用定理,有

例2计算
解csc(z)在所围成的区域内存在孤立奇点z=0,并且该奇点是一级极点,从而z=0是的二级极点.
例3计算
解所围成的区域内存在孤立奇点 i-,由于不存在,所以z=-i 是f(z) 的本性奇点.
将f(z)在内展开成洛朗级数,有