精准回归优于逐步回归的经典一例

◆俞钟行 / 文

在质量管理中常使用回归方法，譬如用excel画个散点图，就可以求出合适的回归方程。当对多个因素建立数学模型时，可能要筛选因素，目前国内外常用的方法是逐步回归，因其简单易用、软件易得。但实际上，国外文献资料[3]已多见对逐步回归法的批评，如“没有程序保证任意大小的回归模型的‘最佳’子集将被识别出来，并且缺乏经验的分析者在经过这逐步的程序后，可能会认为找到了某种意义上最优的模型”。另外，可用于逐步回归的工具如SAS软件，也不是我国绝大多数企事业单位能实际应用的。本文提供了新的可操作思路。

一、原例[1-3]及逐步回归分析结果

假设某种水泥在凝固时所释放的热量Y(卡/克)与水泥中下列四种化学成分有关。

x1——3CaO•Al2O3的成分（%）；

x2——3CaO•SiO2的成分（%）；

x3——4CaO•Al2O3•Fe2O3的成分（%）；

x4——2CaO•SiO2的成分（%）。

共观测了13组数据（见表1）。试求出Y与x1,x2,x3,x4的回归方程，并对该回归方程和各个回归系数进行检验。

表1 水泥数据

以SAS/STAT软件中最常用的REG来完成逐步回归的计算，得回归方程：

复相关系数R=0.989293，

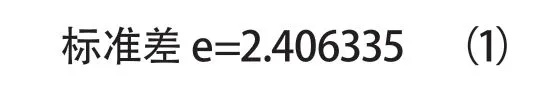
二、对原例运用精准回归分析[4]

原例就是一系列试验，现用已形成套路的因素趋势法进行分析。

1.对表1中的数据，按正交试验中的方法做“不等水平的极差分析”，具体如下。

对x1来说，它13次试验只包含7个不同水平，分别是1、2、3、7、10、11、21。类似的x2含12个，x3含9个，x4含11个不同水平。在计算每一水平的Y值时，可应用excel的“sumif”语句。这里假设x1至x4的4列数据处于excel电子表格的B到E列，Y列数据处于I列，则对应表1中x1列的最低水平“1”的Y值得到：在相应的电子格中输入“=sumif(B$2:B$14,1,$I$2:$I$14)/3”。式中“1”是x1的水平值，共出现3次，所以要除以3。按回车即可得到76.86667。相似操作得到x1的其余6个值：93.1、102.7、87.2、109.4、103.6、115.9，x1的极差值就等于组中最大值减最小值，为39.03333。“sumif”语句在不同位置加$是便于计算其余值时使用拖拉技术。用同样方法继续对x2～x4作极差分析。因为x1～x4各列的水平的个数不同，还要考虑“折算系数”。从任露泉“试验优化技术”p21查到，当极差水平个数为7～10时，必须对原极差乘以系数0.35、0.34、0.32、0.31。本例x1至x4的水平个数为7～12。所以这个“折算系数”对本例的“极差分析”影响不大，暂不考虑。

2.根据x1～x4的极差分析结果，就可以依序（从左到右）画出“因素趋势图”，如图1。

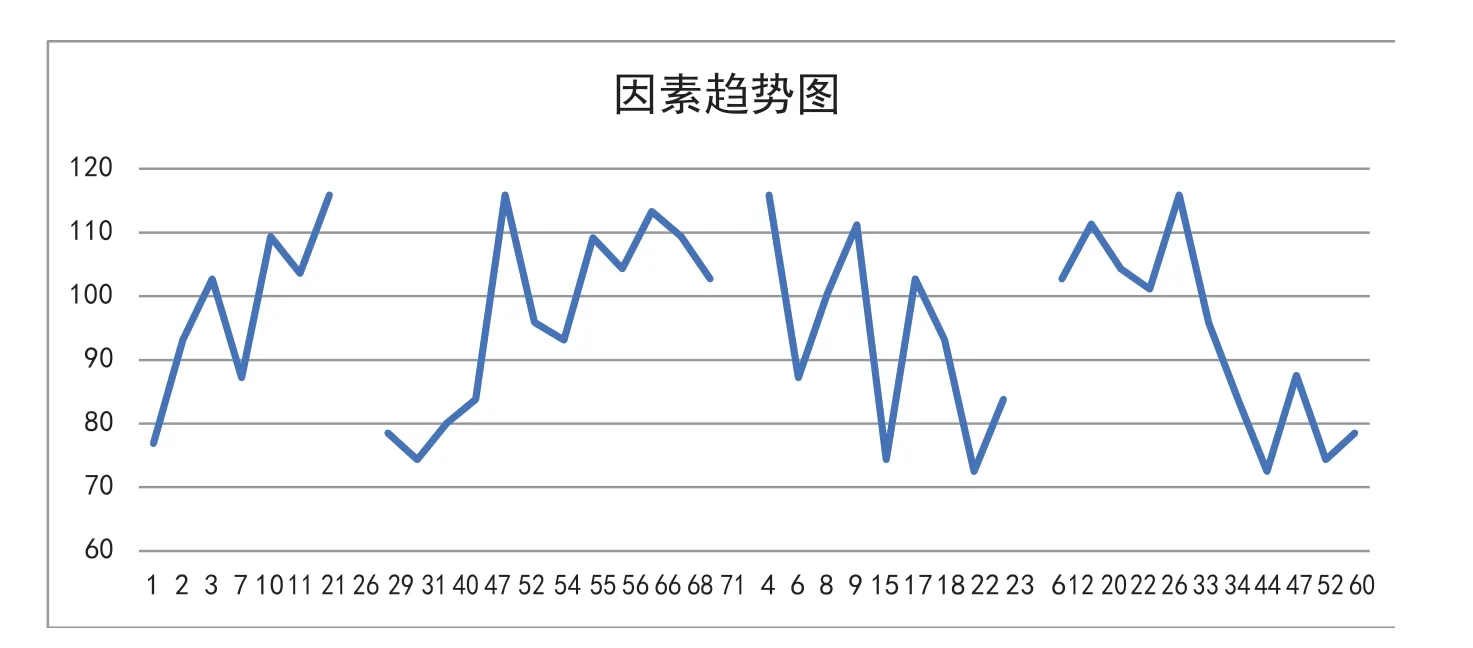
图1 因素趋势图

3.以因素趋势图“导航”做精准回归，这个步骤要有一定的想象力和技巧性。图1给出了4个因素变化趋势的宝贵信息。首先，4个因素（变量）的强度是势均力敌的。而且看到，前两个因素x1和x2有向上的总趋势；后两个因素x3和x4有向下的总趋势。我们知道，趋势向上与趋势向下的两个因素之间容易产生交互作用。此外，x3的因素趋势图颇有三角函数cos的周期变化相貌。所有这些，让我们对表1中数据如何实施“变项”和“插项”的策略有了设想。在excel的电子表格里，可以用“数据分析”中“回归”模块来分析表1中的数据。具体操作时可以分几步做，比如先把表1中x3列数据改为cos(x3)，于是数据第1行的cos(6)=0.96017，等等。然后做回归分析，若发现得到的回归方程性能指标有显著的改进，就证明这步“变项”是正确的。接着又插了两个“交互项”x2*cos(x3)和x2*x4，最后在excel的电子界面上，数据如表2。

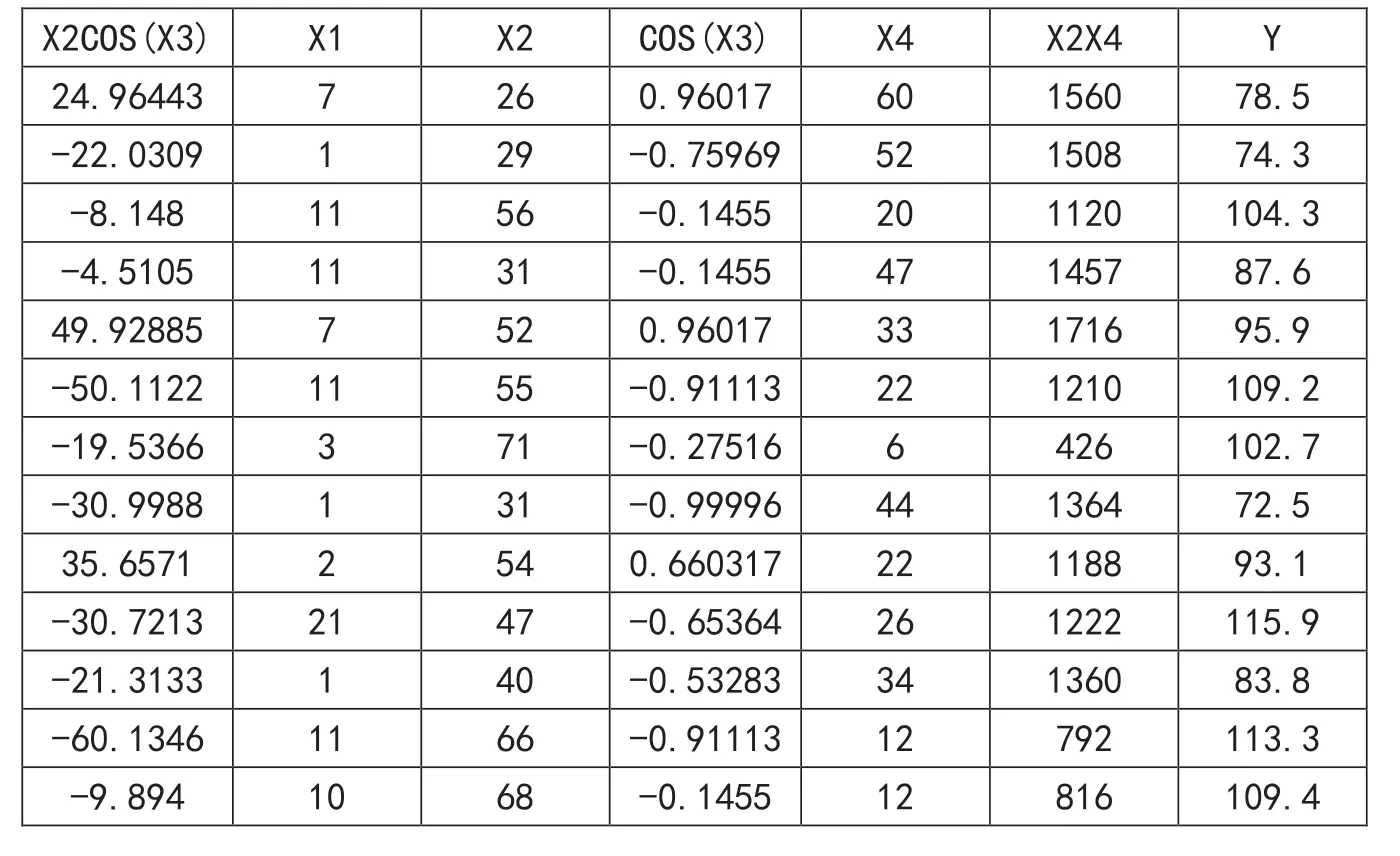
表2 变项、插项后的excel电子表格界面

表2中x2*x4这列第1行的1560，就是x2第1行的26与x4第1行的60的乘积。依次类推。对表2再用excel的“回归”分析，得出结果如图2。

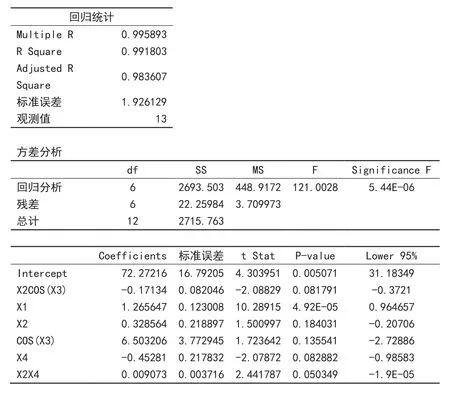
图2 “变项”、“插项”后的回归结果

从上图的Coefficients列里，得知回归方程为：

与用逐步回归得到的方程（1）相比，方程（2）性能指标显著改善了。

因为方程（1）只有2个因素，而方程（2）有6个因素，直接比复相关系数大小并不合理，因此按公式（参见文献4的p56）Ru=1-（1-R）（n+k+1）/(n-k-1)来做比较。上式中，R：复相关系数；n：数据个数；k：excel回归分析的“回归自由度”即“因素个数”。当Ru是正数且数值最大时，回归方程为优。

三、讨论

原例传统经典的变量选取方法，意识到4个自变量间存在较强的相关性，如“当模型中只有x2时，它的最小二乘估计的效力是.789。模型里加进x4后，x2的效力是.311，缩减50%以上。再加入x3、x2的效力改变成-.923”[3]。在画出因素趋势图后，则形象地显示出因素（变量）之间存在的具体的交互作用。又如，“为了得到‘最优’回归方程”，实际采取的方法是“从方程中删除最不重要的自变量，如x3”[1]。但画出因素趋势图后，不但看到x3这个因素并不弱，还看到它呈三角函数的周期性，并且它的向下趋势，与趋势向上的因素还形成交互作用。所以，因素趋势图能给出极有价值的情报，使分析者能通过“变项”、“插项”等技术手段，最后得到拟合优度明显提高的回归方程，如标准误差下降20%、残差平方和下降70%等。方程里有些项的p值超过5%，但根据经验值得保留下来。

表3 回归方程模型有关参数的比较

所谓“精准回归”，就是根据正确画出的因素趋势图，识别各因素的实际态势和交互关系，通过“变项”、“插项”等手段，获得最满意的回归方程。它往往不是原以为的普通线性方程，而是广义的线性方程，更好地勾勒了各变量之间的关系。对这个经典案例，用精准回归优于用逐步回归。即使和其他变量筛选法相比，如向前引入法、向后剔除法及全子集法，精准回归法也是更好的方法。因为它通过正确画出的因素趋势图，可以识别出各因素的真实面貌和相互关系，然后有针对性地搭起数学模型的粗坯，最后用excel的“回归”模块来验证和确认。其它方法，似乎难望其项背。