基于阈值的电动调节阀故障检测方法研究

代希文，周犊，赵桂生，邵浙梁，于新海，周邵萍

（1. 华东理工大学，上海 200237；2. 中广核核电运营有限责任公司，广东 深圳 518000；3. 中广核研究院有限公司，广东 深圳 518000）

阀门在线无故障运行对于系统正常运行至关重要。据统计，一座包含两台百万千瓦机组的核电站每年用于阀门的维护费用高达上亿元，占电站总维护费用的近50%[1]。因此，通过在线监测阀门运行参数，准确及时判别阀门运行状态从而检测出故障，对保障工艺系统安全运行具有非常重要的意义[2]。

故障检测是根据监测参数，通过相关分析判断阀门运行状态好坏的过程[3]。目前有许多学者就阀门故障检测的方法开展研究，并形成了以累计残差法和单指标控制图法等为主的故障检测方法[4-5]。例如，2012 年，黄爱芹等[6]采用累计残差法和3σ残差控制图对气动调节阀的状态进行评估测试，实现了阀门的故障检测。2015 年，张昭[7]通过累计残差法对DAMADICS 阀门仿真平台的故障数据进行检测，并识别出大部分故障。这类方法以单指标参数作为阀门故障检测的标准，具有过程简单、便于解释的优点，然而，单指标评估存在无法对各阀门监测参数做系统分析的缺点，导致实际应用的准确性 差。

随着传感器灵敏度的提高和上位机存储技术的进步，通过传感器对运行状态的阀门进行监测，运用信息融合的方法对多源数据分析和处理成为了新的故障检测的趋势。2019 年，王印松等[8]提出一种基于特征指标信息融合的方法，实现了阀门的故障检测，同年，孙天舒等[9]通过二分类器构建静态特征，相似度表征动态特征的方法，融合静态距离和动态变化等参数，实现了气动调节阀执行机构的故障检测并取得较好的效果。然而，基于多源信息融合的方法需要大量的监测参数与现场数据，并且针对复杂工况下的电动调节阀故障检测的现场实验研究相对较少，通常仅通过仿真模拟信号进行实验验 证。

因此，本文结合统计分析和多源信息融合两种方法的特点，基于阀门专家大量运维经验，提出一种适用于电动调节阀的基于阈值的故障检测方法。为了验证该算法的有效性，搭建电动调节阀的在线监测平台，对填料过紧、润滑条件异常、阀杆弯曲、阀座异物附着、阀芯或阀座损坏等5 类故障原因引起的阀门卡涩故障进行实验。针对测试信号的信噪比低和信号微弱等问题，使用均值滤波和S-G 滤波对原始信号去噪处理，较明显地分辨出阀门信号的有效特征；再使用时域频域分析提取故障特征参数，通过实验验证基于阈值的故障检测方法的有效性。

1 数据处理与故障检测算法

1.1 S-G滤波降噪算法

由于阀门常处于振动、噪声的工作环境，且因工作平台各部件的相互影响，导致采集到的信号存在信噪低、信号微弱的问题，因此，对传感器采集的各类信号实施信号处理和特征提取是极为重要的。

本文采用平滑滤波算法对数据降噪。常见的平滑处理方法有滑动平均法（Mean Average）、指数滑动平均法（Exponential Mean Average）、S-G 滤波法（Savitzky Golay Filter）三种。滑动平均法适用于真实值变化不大或线性变化的场景，且效果受滑动窗口大小影响较大，信号存在滞后观测值的问题；指接近当前时刻的观测值。但实验数据波动较小时，该算法鲁棒性较差；S-G 滤波法具有滤除噪声的同时，可以确保信号的形状、宽度不变的特点，是一种在时域内基于局域多项式最小二乘法拟合的滤波方法，适合于实验数据信号[10]。因此，本文通过S-G 滤波对工况干扰进行滤除。设样本数据为x（p），其中的一组数据为x（i），i=-J，…0，…J， S-G 滤波是用多项式f1来拟合这组数据，如式（1）所示[11]：

式中n——设定的多项式阶数，且n≤2 J。

在拟合的过程中，会存在一定的拟合误差，设总误差的平方和为E，通过式（2）表示为[12]：

为使滤波前后的波形尽可能保留原始特征，需要拟合的误差尽可能小，为此，可令E对各系数的导数为零，由此得到式（3）：

式中，r= 0， 1， …n，令Fr和Sk+r定义为式（4）与式（5）：

则式（3）可改写为：

根据式（6），只需给定拟合的单边数J，多项式的阶数n和原始样本数据x（p），即可确定S-G 滤波的拟合多项式f1，计算得到滤波后的波形信号。

1.2 故障检测检验标准

在对原始样本数据进行降噪处理的基础上，为定性定量地分析故障检测模型的好坏，判断模型的偏差大小，需要引入相关参数评估模型的性能。由于阀门故障检测是检测有无故障，本质也属于分类问题，因此本文引入准确率、召回率、精确率和F1值作为评判阀门故障检测模型的参数[13]。通常以关注的类为正类，其他类为负类，分类器在数据集上的预测或者正确或者不正确，我们有4 种情况：

TP（True Positive）：把正类预测为正类；

FP（False Positive）：把负类预测为正类；

TN（True Negative）：把负类预测为负类；

FN（False Negative）：把正类预测为负类。

以判断阀门故障样本为例，若以发生故障的样本记为正类，则分类模型中发生故障并被正确分类的样本个数记为TP，发生故障但被错误分类为正常状态的样本数量记为FP，正常状态并被正确分类的样本数量记为TN，正常状态但被错误识别为故障状态的样本数量记为FN。

对于给定的测试数据集，准确率是分类器正确分类的样本数与总样本数之比，如式（7）所示：

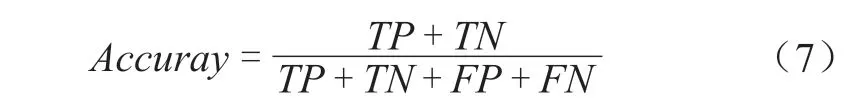
召回率是所有正确分类的样本数占应被判断为正确的样本数之比，如式（8）所示：

精确率是正确预测为正样本数的占全部预测为正的比例，如式（9）所示：

F1值为算数平均数除以几何平均数，如式（10）所示：

1.3 基于阈值的故障检测方法

为判断阀门状态，结合阀门专家大量运维经验，并基于实验阀门参数的基础上，建立了基于阈值的评估方法，其规则逻辑如下：

规则一：若实验阀位处于0% ～ 5%与95% ～ 100%的区间，则进入规则二继续诊断；若实验阀位处于5% ～ 95%，此时测到的推力记为F2，计算得到的与正常状态下在该阀位的阀杆推力F1比较，若F2＜0.85F1或者F2＞1.15F1，则判断阀门出现故障，反之则进入规则二进一步判断。

规则二：通过阀位计算正常状态下阀位波动的幅值，记为X1，实验状态下的阀位波动的幅值记为X2，若X2＞1 + 0.3X1，则判断阀门出现故障，反之进入规则三判断。

规则三：将正常状态的阀位信号做FFT 变换得到阀位的波动频率，记为f1，实验状态下阀位波动的频率记为f2，若f2＞1.1f1或f2＜0.9f1则判断阀门出现故障，反之认为阀门处于正常运行状态。

在确定好规则库的逻辑后，建立的判别流程图如图1 所示。

图1 基于阈值的电动调节阀有无故障的判别流程图Fig.1 The flow chart of the judgment of whether the electric regulating valve has faults based on the threshold

2 实验研究

2.1 在线监测实验平台搭建

为了验证故障检测模型的有效性和准确性，本文进行了故障模拟实验，作为评估模型建模和验证的基础。为模拟阀门在正常和故障的运行状态，获得阀门的实时工作状态并获得在线数据，需搭建在线监测实验平台。实验平台分工作回路模块与数据采集模块两部分，工作回路模拟调节阀的实际工况，并通过数据采集模块得到阀门在不同状态下的运行参数。

（1）工作回路模块

调节阀工作回路用于模拟在不同介质压力阀门的运行工况。为模拟电动调节阀故障状态和正常状态，实验选取ZAZP-16K 型号阀作为试验阀门，依托某企业的的阀门运行回路，完成了电动调节阀的在线监测装置的设计和搭建。故障模拟实验装置工作回路示意图如图2 所示。该装置有主回路和辅助回路两部分组成，主回路是通过试验阀的回路，用于测试不同条件下阀门的工况，并通过进出口压力表和温度计读取阀门前后管道压力和介质温度；辅助回路用于在实验前调试水压状态，保证介质压力的稳定性。

图2 故障模拟实验装置工作回路图Fig.2 Working circuit diagram of fault simulation experimental device

（2）数据采集模块

在完成搭建电动调节阀工作回路的基础上，为了能在线监测阀门的实时状态，还需要搭建在线监测和数据采集模块。如图3 所示为电动调节阀数据采集系统的工作原理示意图，该部分由传感器采集和中间件处理两部分构成。

图3 数据采集模块工作原理示意图Fig.3 Schematic diagram of the working principle of the data acquisition module

其中，传感器采集部分包括以下部件：光栅光纤传感器测量阀杆推力和填料螺栓紧固力；分压传感器测量电动头电压；电流钳测量电动头电流；拉线位移传感器测量阀杆位移；智能电流表结合串口通讯软件测量调节阀输出阀位。中间件处理部分包括光纤解调仪、NI9201 采集卡、cDAQ-9170 卡槽，用于对以上监测参数传输与处理，并输入到上位机中。

2.2 故障模拟

结合阀门卡涩常见的故障原因，实验过程中模拟填料过紧、润滑条件异常、阀杆弯曲（阀杆光柱弯曲、阀杆螺纹处弯曲、阀杆填料处弯曲）、阀座异物附着、阀芯或阀座损坏5 类故障，采集参数包括阀杆推力、阀杆位移、电动头的电流与电压、电动头输出阀位、填料螺栓紧固力共6 个参数。

（1）阀杆弯曲

为模拟该故障，实验使用外力将三根阀杆分别在阀杆光柱处、螺纹处和阀杆填料密封处进行弯曲变形，如图4a、b 所示。弯曲程度及弯曲部位如表1 所示。

表1 实验阀杆加工参数Table 1 Processing parameters of experimental valve stem

（2）填料过紧

试验通过扭矩扳手将两个填料螺栓扭矩调节至40 N·m 来模拟填料过紧故障导致的阀门卡涩现象，如图4c 所示。

（3）润滑恶劣

为模拟该异常工况，试验在断电条件下顺次拆除电动装置，将传递扭矩的蜗轮蜗杆周围的润滑脂用酒精清除，如图4d 所示。

（4）阀芯磨损

实验通过在正常阀杆的阀芯两端对称点焊两个焊点来模拟阀芯磨损故障，如图4e 所示。

（5）异物卡住

实验通过在阀芯底部裹上2 mm 的纤维布并用细铁丝固定来模拟阀芯异物卡住故障，如图4f 所示。

图4 故障模拟图Fig. 4 Analog fault

2.3 实验样本处理

根据上述故障模拟方案进行实验，完成卡涩故障的数据采集和分析。为保证实验数据仅受单一故障原因的影响，实验选择做相同压差下正常状态的工况作为比较，且每种压差条件做3 组实验，尽可能避免偶然条件带来的误差。出于阀门故障检测的需要，对每种故障在常温下阀前阀后压差分别为0.4 MPa、0.8 MPa、1.2 MPa、1.6 MPa 下进行阀位全开行程和全关行程的实验。通过实验得到6 种不同故障状态和正常状态在不同压差下共计96 组实验数据。其中每组数据约有7 000 个样本点，共计约700 000 个数据点。部分实验得到的数据表2 所示。

表2 部分实验样本数据Table 2 Partial experimental sample data

3 结果与讨论

3.1 信号去噪效果

在现场数据采集的过程中，由于380V 工电干扰及管道水流不稳定的情况，导致阀杆位移会出现非正常振动。需要通过均值滤波-S-G 滤波方法对信号采取降噪处理，提取有价值的趋势项。实验采集样本为10 Hz，且大部分样本数据围绕趋势项上下波动，少部分奇异值较大。

考虑到以上数据特点，本文先对信号均值滤波处理，滤波窗口大小设定为5，消除大多数偏离值，再使用平滑滤波算法平滑降噪。经均值滤波和S-G滤波前后得到的结果如图5 所示。从图中可以看出，S-G 滤波算法去噪效果显著，并很好地保留了有用信号的特征。

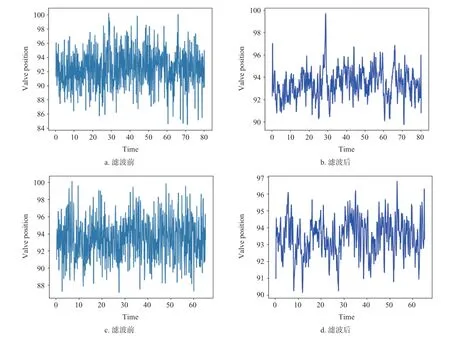
图5 S-G 滤波前后对比图Fig. 5 Comparison S-G filtering

考虑到执行机构电压是奇异样本数据，与其他样本特征相差较大，所以需要对原始数据做归一化处理。由于数据总体样本并不符合正态分布规律，且总体数据比较集中，所以选取最大最小标准化法是非常合适的。归一化方法如式（11）所示：

式中x——样本特征参数；

max （x）——样本中稳定的最大值；

min （x）——样本中稳定的最小值；

x'——归一化后的特征参数。

3.2 阈值法故障检测效果

在对原始数据降噪处理的基础上，为验证模型的可行性，本文选取实验得到的故障数据和正常状态的数据对模型测试。首先选取一组0.4 MPa、0.8 MPa、1.2 MPa、1.6 MPa 压差下正常状态的行程和阀杆推力作为正常样本输入到模型中，并计算得到阀位的平均波动幅值，波动频率及阀杆推力，并将正常状态的阈值保存至模型中。由于阀门阀位信号的直流分量较大，使得信号做傅里叶变换后零频幅值过大而湮没了特征频率，故通过将信号的每个数据减去数据均值来消除零频信号干扰，然后将信号做快速傅里叶变换（FFT 变换）得到阀位的波动频率[16-17]。

随后将实验样本作为测试样本输入到模型中，验证模型的性能。测试样本包括正常状态、阀芯异物、填料过紧等6 种运行状态、并分别含有0.4 MPa、0.8 MPa、1.2 MPa、1.6 MPa 四种压差状态下的数据。每种运行状态含有12 组样本，共计96 组样本，并分别计算得到各个状态下的阀杆推力、阀位振幅、波动频率，部分状态的波动频率频谱图如图6 所示，从图中可以看出，FFT 变换能较好地绘制出各故障的频谱图。正常状态下阀位波动频率在0.2 Hz 左右，螺纹处弯曲的波动频率为0.18 Hz，与正常状态相差不大，阀杆填料处弯曲和阀芯磨损的频率则明显增大。异物卡住波动频率为5 Hz，与正常状态相差巨大。

根据阈值法对所有样本数据进行测试，得到的测试结果如表3 所示。从表中可以看出，评估模型将36 组的阀杆弯曲和12 组阀芯点焊故障全部识别出来，对填料过紧、润滑恶劣和异物卡住也有很好的辨别效 果。

表3 阈值法评估实验结果Table 3 Threshold value method to judge whether there is a fault

将测试样本输入到模型中，将有故障和无故障作为正样本，得到的模型评估结果如表4 所示。从表中可以看出，当有故障作为正样本时，模型的准确率高达92.6%，且精确率、召回率、F1 值均达到85%以上，说明模型对有故障的阀门状态辨别能力高；当将无故障作为正样本时，准确率高达92.6%，测试得到该方法满足电动调节阀的故障检测条件。

表4 阈值法模型评估结果Table 4 Threshold method model evaluation results %

4 结束语

本文基于多年的经验提出一种基于阈值的故障检测方法，搭建电动阀门在线监测平台，以ZAZP-16K 型号的电动调节阀作为实验对象，实验模拟5 类故障原因引起的卡涩故障，通过监测相关参数获得实验数据。针对信号弱和信噪比低等问题，使用了一种基于均值滤波和S-G 滤波的阀门数据处理方法，实验验证了基于阈值的电动调节阀门故障检测方法的可行性，从而实现电动调节阀在不同阀位下判断阀门有无故障的功能。