掺杂石墨烯纳米片对硝酸钠相变特性的影响及机理*

吕浩翔 冯黛丽 冯妍卉 张欣欣

(北京科技大学能源与环境工程学院,冶金工业节能减排北京市重点实验室,北京 100083)

纳米增强剂通常被用来提升相变材料的导热性能,但这种方式通常伴随着复合后材料相变焓的降低.虽然这种降低难以避免,但其微观机理乃至影响规律却始终未能明晰.为深入探究纳米复合相变材料相变焓降低的机理,本文以熔融硝酸钠(太阳盐的重要组成成分)为相变材料,制备了石墨烯纳米片质量分数为0%,0.5%,1%,1.5%,2%的复合相变材料.通过实验测量与分子动力学模拟的方法深入分析了石墨烯纳米片的掺杂导致熔融硝酸钠产生团簇以及复合材料熔点和相变焓非依数性降低的影响机理.结果表明,石墨烯纳米片质量分数为1.5%时,硝酸钠致密层和石墨烯纳米片间的质心等效距离最接近他们相互作用势的势阱位置,此时二者之间相互吸引作用最强,熔盐分子的运动受限最为严重,难以发生熔化,从而导致相变焓降低最为显著.为了最大限度地避免纳米复合相变材料相变焓的损失,应根据相变材料与纳米增强剂的类型及其相互作用类型,合理选择纳米增强剂的质量分数.在实际应用中,恰当的质量分数还将在一定程度上降低复合相变材料的制备成本.

1 引言

熔盐制备成本低,具有良好的热性能和较低的蒸汽压,作为传热流体和热储能介质(TES)被广泛应用于聚光太阳能(CSP)装置中[1].其中熔融硝酸盐由于具有较好的热稳定性和相对更低的成本是最常用的盐类[2].为了提高TES 的热容量,已经提出了一系列方法来改善热特性[3],如降低熔点和提升热导率[4−6].自从Shin 和Banerjee 通过掺杂二氧化硅纳米颗粒使得四元氯化物共晶盐的比热增加15%,二元碳酸共晶盐的比热增加24%以来[7,8],添加纳米颗粒改善熔盐相变热特性的方法就得到了广泛的推广和尝试[2,9−13].相变焓作为熔盐相变热特性的重要指标,在引入纳米颗粒掺杂后的熔盐体系中却表现出增强或减弱的两种相反趋势,且目前文献中对于熔盐相变焓异常变化的原因尚不明确[1,11,14,15].最近的研究指出,纳米颗粒掺杂后熔盐中存在致密的压缩液体层,压缩液体层内熔盐的性质与层外熔盐存在一定的差异[2,10,13].然而,目前的研究对于压缩液体层的形成机理及其对熔盐基复合相变材料相变热特性的影响规律并未进行深入探讨.

因此,本文针对掺杂纳米颗粒的熔盐基复合相变材料相变热特性的变化展开研究,并利用分子动力学模拟方法进一步讨论压缩层的形成机理及其对复合相变材料相变特性的影响规律.从分子间相互作用类型及势阱深度的角度阐释了压缩层的形成机理以及相变热特性的非依数性变化,旨在通过本文的工作对于未来纳米颗粒的种类及掺杂比的选择提供一定的指导.为了更直接地探明纳米颗粒与熔盐之间的相互作用,排除不同盐类之间相互作用的影响,本文选取太阳盐组分中具有较高相变焓(172 J·g–1)[16]的硝酸钠作为单一的相变芯材.具有超高热导率(约5000 W·m–1·K–1)和高比表面积(约2630 m2·g–1)[17]的石墨烯纳米片兼备优异的力学性能以及优良的化学和热学稳定性[18],被认为是最有前途的改善相变材料热性能的纳米颗粒.考虑到单层石墨烯的引入在降低相变材料过冷度方面的表现优于多层石墨烯[19],本文选取单层石墨烯纳米片作为纳米增强剂开展工作.

2 实验制备及测试方法

2.1 样品制备

以纯度为98.5%的硝酸钠作为复合相变材料的基材,厚度为6—8 nm、平均直径为15 µm 的片层状石墨烯纳米片作为纳米增强剂制备了纳米片质量分数为0%,0.5%,1%,1.5%,2%的石墨烯纳米片@硝酸钠(GNS@NaNO3)复合相变材料(Pure NaNO3,0.5%GNS@NaNO3,1%GNS@NaNO3,1.5%GNS@NaNO3,2%GNS@NaNO3).制备流程参照Jo 和Banerjee[9]的方法,并进行了一些调整,具体如图1所示.首先在蒸馏水中加入石墨烯纳米片与阿拉伯树胶,而后将悬浮液置于电磁搅拌器中搅拌10 min以保证石墨烯纳米片的均匀分散(650 r·min–1,常温).完成搅拌后,将悬浮液置于超声发生器中超声处理(40 Hz) 90 min,以使石墨烯均匀分散,并降解阿拉伯树胶.随后将硝酸钠加入经超声处理过的石墨烯纳米片悬浮液中,并将混合后的硝酸钠-石墨烯纳米流体置入超声处理器中超声处理180 min,以使硝酸钠与石墨烯纳米片充分混合形成复合纳米流体.完成超声处理后,将溶液置于培养皿中在热板上快速蒸干,以减少完全蒸发的持续时间,防止石墨烯纳米片的凝聚.最后在培养皿中残余少量水分时将培养皿放入鼓风干燥箱中加速干燥,以保证得到石墨烯纳米片均匀分散的复合相变材料.

图1 石墨烯纳米片@硝酸钠复合相变材料的制备流程Fig.1.Preparation process of GNS@NaNO3.

2.2 表征及蓄热性能测量方法

采用FEI (型号Quanta 450 FEG)扫描电子显微镜(SEM)对GNS@NaNO3复合相变材料的表面形貌进行研究.为更好地观察石墨烯纳米片在熔盐中的分散情况,选取×5 k 的放大倍数.

GNS@NaNO3复合相变材料的熔融和蓄热行为采用带冷却模块的梅特勒-托利多差示扫描量热仪(DSC)进行研究.测试过程由室温升至350 ℃,升温速率设定为5 ℃·min–1.取蒸干后的复合相变材料5—10 mg 置于标准陶瓷坩埚中进行测量.样品熔化后迅速将其冷却至室温以得到热流变化曲线.

3 GNS@NaNO3 复合相变材料表征及蓄热性能测量结果

3.1 GNS@NaNO3 复合相变材料的形貌

纯硝酸钠以及掺杂不同质量分数石墨烯纳米片的复合相变材料的表面形貌如图2 所示.从图2(b)—图2(e)可以看出,石墨烯纳米片在硝酸钠中分散良好.实际上,当纳米片质量分数较小时,纳米片更像是附着在硝酸钠表面.但随着质量分数的增加,纳米片附近的熔盐包裹在石墨烯纳米片表面形成了团簇状的致密结构.

图2 石墨烯纳米片@硝酸钠复合相变材料的扫描电子显微照片 (a)石墨烯纳米片;(b) 纯硝酸钠;(c) 纳米片质量分数为0.5%的石墨烯纳米片@硝酸钠;(d) 纳米片质量分数为1.0%的石墨烯纳米片@硝酸钠;(e) 纳米片质量分数为1.5%的石墨烯纳米片@硝酸钠;(f) 纳米片质量分数为2.0%的石墨烯纳米片@硝酸钠Fig.2.Scanning electron micrograph of GNS@NaNO3:(a) GNS;(b) pure NaNO3;(c) GNS@NaNO3 when GNS weight concentration is 0.5%;(d) GNS@NaNO3 when GNS weight concentration is 1.0%;(e) GNS@NaNO3 when GNS weight concentration is 1.5%;(f) GNS@NaNO3 when GNS weight concentration is 2.0%.

3.2 GNS@NaNO3 复合相变材料的蓄热性能

纯硝酸钠及复合相变材料的热流测量结果如图3 所示.由纯硝酸钠的吸收峰得出其熔点为308 ℃,相应的相变焓约为174 J·g–1[20].有趣的是,掺杂石墨烯纳米片后的复合相变材料熔点略有下降,但相变焓却出现了显著的下降.同时可以观察到,复合相变材料相变焓的下降与石墨烯纳米片的质量分数存在一定的关系但并未呈现出依数性,类似的情况同样出现在Engelmann 和Hentschke[13]的研究中.在石墨烯纳米片质量分数为1.5%时复合相变材料的相变焓下降最为明显,由原本的174 J·g–1降为147.72 J·g–1.

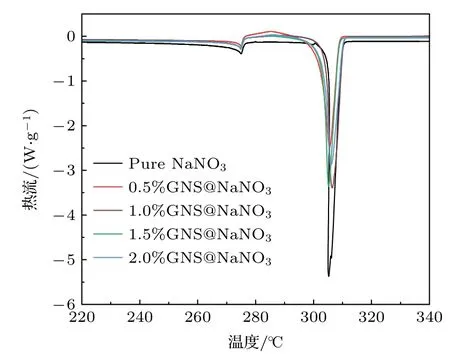
图3 硝酸钠和石墨烯纳米片@硝酸钠复合相变材料的热流曲线Fig.3.Heat flow curves of pure NaNO3 and GNS@NaNO3.

为更好地对比不同样品的相变焓与石墨烯纳米片质量分数之间的关系,计算了表观蓄热效率,定义为复合相变材料的实际相变焓与理论相变焓的比值:

式中,θ表示表观蓄热效率,w表示石墨烯纳米片的质量分数,HS,comp和HS,PCM分别代表复合相变材料和硝酸钠的相变焓.如表1 所列,复合相变材料的表观蓄热效率均低于100%,且在石墨烯纳米片质量分数为1.5%时最低,仅为86.19%.结合复合相变材料的表面形貌不难得出结论,石墨烯片附近团簇的硝酸钠熔盐并未参与熔化,从而导致了复合相变材料相变焓的降低.

表1 硝酸钠和石墨烯纳米片@硝酸钠复合相变材料的相变热性能Table 1.Phase change characteristics of pure NaNO3 and GNS@NaNO3.

4 石墨烯纳米片掺杂对硝酸钠熔盐相变特性的影响机制

上述实验结果表明,石墨烯纳米片的掺杂导致部分硝酸钠熔盐在纳米片附近形成了致密的团簇结构,从而阻碍了熔盐的熔化,体系的熔点与相变焓均有所降低.但相变焓的降低并未呈现出对石墨烯纳米片质量分数的依数性关系,即相变焓并非随纳米片质量分数的增加而线性降低.为进一步探索复合材料相变焓非依数性降低的微观机理,建立了复合相变材料的微观结构模型,利用分子动力学模拟方法从体系内原子位置分布、分子间相互作用的类型及强度等角度进行阐释.

4.1 模型构建及方法

以石墨烯纳米片质量分数为1.0%的复合相变材料为例,其结构模型见图4.石墨的结构参照Materials Studio 结构库中的石墨结构模型进行构建(a=b=2.46 Å,c=6.80 Å).随后在石墨初始构型的基础上建立超胞,并取单层石墨分子作为石墨烯纳米片的结构模型.硝酸钠单胞取自晶体库,随后对其超胞得到硝酸钠结构模型.硝酸钠纳米结构模型的可靠性通过对比硝酸钠熔点的模拟结果与实验结果证实[21].为了模拟石墨烯纳米片在硝酸钠中的均匀弥散,复合材料模型的构建采取将边长为10 Å的石墨烯纳米片随机引入硝酸钠结构模型的方法.在构建掺杂不同质量分数纳米片的复合材料模型时,保持体系的大小为60 Å × 60 Å× 60 Å不变,在模拟盒子中按照特定的质量百分比填充硝酸钠以及石墨烯纳米片.

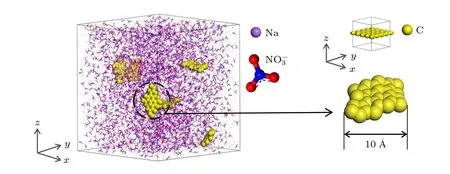
图4 石墨烯纳米片质量分数为1.0%的石墨烯纳米片@硝酸钠复合相变材料结构模型Fig.4.Structural model of GNS@NaNO3 when GNS weight concentration is 1.0%.

本文所有模拟工作均通过LAMMPS 平台开展[22].采用分子动力学模拟探究纯硝酸钠及石墨烯纳米片质量分数为0.5%,1.0%,1.5%,2.0%的复合相变材料相变热特性变化的微观机理.选用周期性边界条件,时间步长设置为0.1 fs,截断半径设置为11 Å.体系首先在热等压系综(NPT)中弛豫100 ps 以达到初始平衡,弛豫温度设定为600 K.相互作用能、分子数密度分布等计算结果的获得通过在微正则系综(NVE)中处理200 ps 实现.

硝酸钠分子间的相互作用以Buckingham 势和Coulombic 势修饰,库仑相互作用的长程修正计算使用PPPM 方法[10],表示为

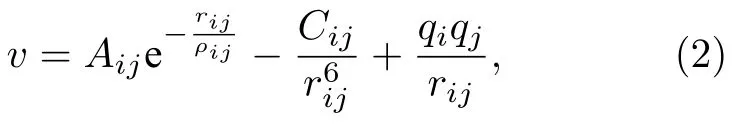
式中,A,ρ,C是长度与能量相关的常数项;v是相互作用能;r是点i和j之间的距离;qi和qj分别是点i和j处的原子电荷量.与此同时,为保持硝酸盐的平面分布,柔性硝酸根分子内部的相互作用(键、角和反常二面体势)以harmonic 势[13]来描述,表示为以(3)式计算的键以及以(4)式计算的角和反常二面体相互作用:

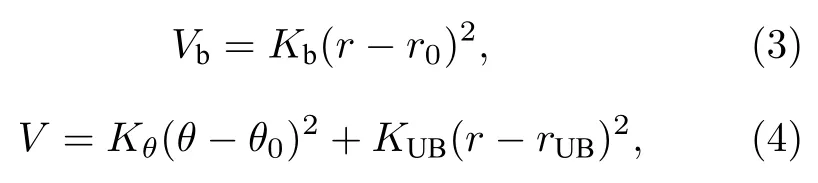
式中,r和θ分别代表键的长度和角度;Kb,Kθ和KUB分别为键长、键角以及Urey Bradley 项的力常数;r0和θ0分别为平衡态下的键长以及键角;rUB代表Urey Bradley 项的平衡距离.采用AIREBO力场[23]来描述石墨烯纳米片内部C—C 之间的相互作用力,硝酸钠与石墨烯之间的相互作用可以用Lennard-Jones (L-J)势函数[24]体现,公式如下:

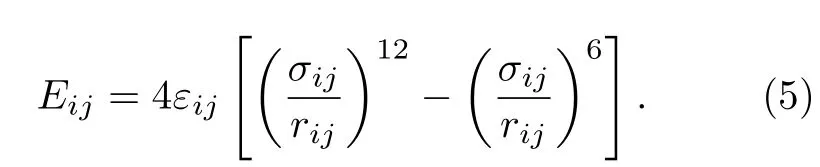
根据标准Lorenz-Bethelot 混合原则,εij采用几何平均值,σij采用算术平均值,表达式如下:

式中,εij代表原子i与j之间的相互作用强度,σij是原子i和j之间的距离[25,26].详细的力场参数列于补充材料(online).

4.2 复合相变材料的均方位移

通过计算复合材料均方位移(MSD)的变化对其熔点下降的现象给出相应机理解释.均方位移可以在一定程度上反映纳米增强剂与相变材料之间的相互作用,可通过下式计算得到:

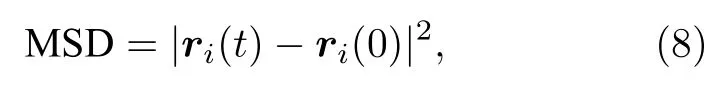
式中,ri(t)和ri(0)分别表示分子i在时刻t和时刻0 的位置向量.

图5 所示为不同纳米片质量分数的复合材料在300 K 下的均方位移随模拟时间的变化.模拟过程在NPT 系综下进行,保持各体系的温度一致,对体系内原子赋予初始速度后弛豫100 ns,期间输出体系的MSD.

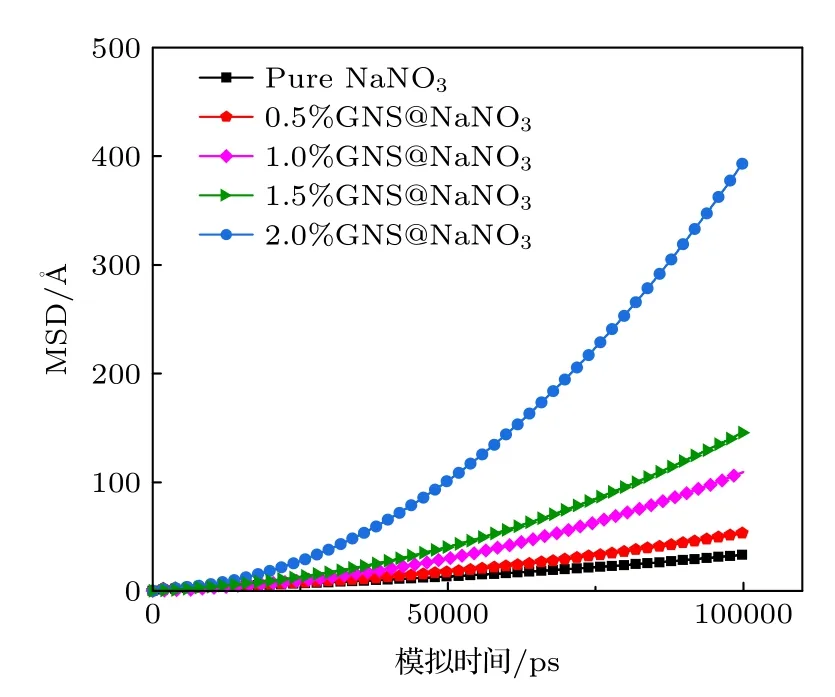
图5 石墨烯纳米片@硝酸钠复合相变材料300 K 下的均方位移Fig.5.MSD of GNS@NaNO3 composites at 300 K.

从图5 可以看出,随着模拟过程的进行,各体系的均方位移逐渐增大.且随着石墨烯纳米片质量分数的增加,体系均方位移的增长速率显著提升.自扩散系数D是随温度T发生变化的函数,该系数的值越大,说明体系内粒子扩散得越快即体系内粒子的流动性越强.考虑到均方位移MSD 计算过程中已对体系内的粒子数做了平均,自扩散系数D可简化为MSD/6.由此可知,均方位移斜率越大意味着自扩散系数越大.这说明纳米片的引入削弱了硝酸钠内部分子间的相互作用,体系内硝酸钠分子无规则运动加剧,平均自由程增大,原子迁移率增高,分子间碰撞频率增大,从而降低了其熔点.

4.3 石墨烯纳米片附近硝酸钠熔盐的分布

首先通过600 K 下体系内的原子位置分布来从微观层面描述硝酸钠熔盐在石墨烯纳米片附近的团簇情况.以石墨烯纳米片作为坐标原点.从图6可以看出,有更多的硝酸钠分子出现在石墨烯纳米片附近,且存在2—4 Å的致密层.这与实验观察到的大量硝酸钠分子团簇在石墨烯纳米片表面的现象一致,表明确实存在部分硝酸钠熔盐未发生熔化行为,从而导致了复合相变材料的实际相变焓低于理论值的现象.

图6 石墨烯纳米片附近的原子分布(纳米片质量分数为1.5%的石墨烯纳米片@硝酸钠)Fig.6.NaNO3 atomic distribution close to GNS (GNS@Na NO3 when GNS weight concentration is 1.5%).

同时可以观察到,在不同质量分数下,石墨烯纳米片附近熔盐致密层的厚度存在一定差异.我们统计了不同纳米片质量分数下复合相变材料内部硝酸钠致密层到石墨烯纳米片的质心等效距离,结果如表2 所列.

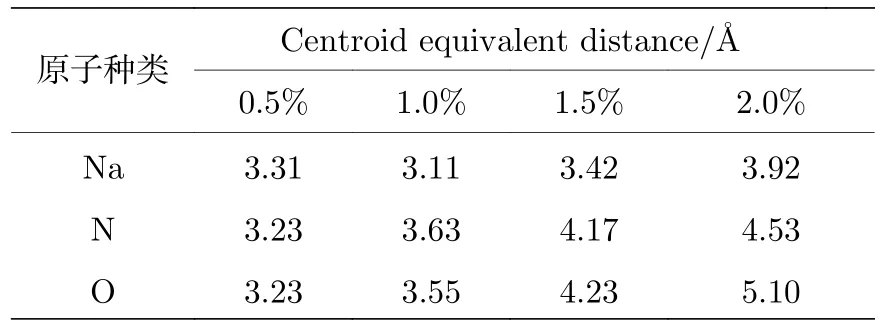
表2 各原子到石墨烯纳米片的质心等效距离Table 2.Centroid equivalent distance of atoms in NaNO3 dense layer to GNS.

考虑到石墨烯纳米片与硝酸钠之间仅存在以L-J 势修饰的范德瓦耳斯相互作用,二者之间的作用力强度与其距离密切相关.硝酸钠熔盐各原子与石墨烯纳米片之间L-J 势的平衡位置分别为r0C-Na=3.071 Å,r0C-N=3.656 Å,r0C-O=3.283 Å,势阱位置re=1.123r0分别为reC-Na=3.45 Å,reC-N=4.11 Å,reC-O=3.68 Å.石墨烯纳米片与硝酸钠之间相互作用的强弱随着二者之间距离的变化而发生变化.图7 为石墨烯纳米片质量分数为1.0%和1.5%的复合相变材料内部原子间L-J 相互作用示意图.通过对比两种掺杂比石墨烯纳米片附近硝酸钠致密层的质心等效距离在L-J 势函数曲线的位置得出结论:当石墨烯纳米片质量分数为1.0%时,C-N 间相互作用为斥力,C-Na 和C-O 间为极弱引力,此时二者之间吸引力最小,石墨烯纳米片对硝酸钠相变潜热的影响最弱;当石墨烯纳米片质量分数为1.5%时,C-N,C-Na 和C-O 间距离均接近势阱位置,存在较强引力,此时二者间吸引力最大,石墨烯纳米片对硝酸钠相变潜热的影响最强.

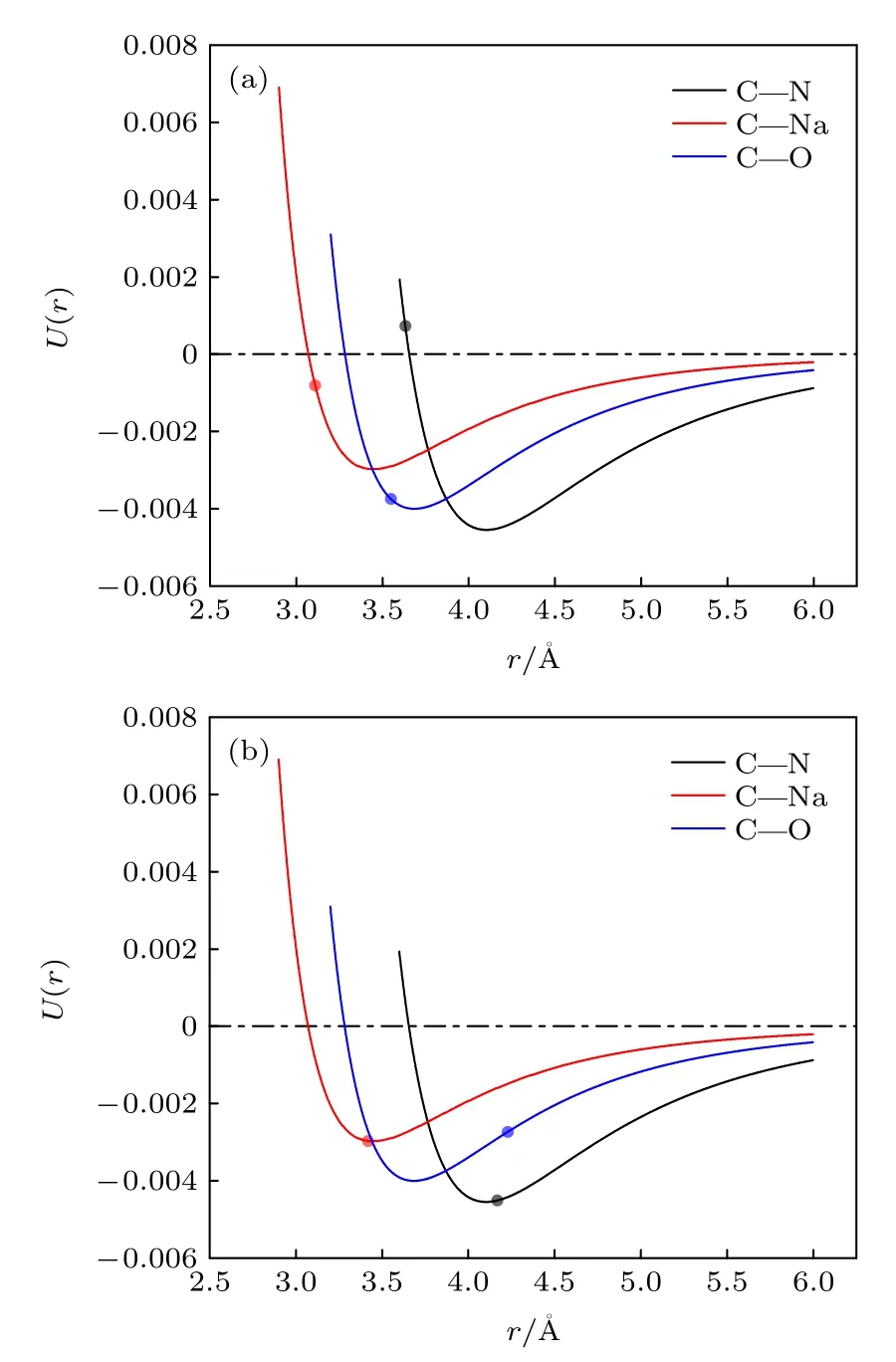
图7 石墨烯纳米片@硝酸钠原子间L-J 相互作用示意(a) 石墨烯纳米片质量分数为1.0% 的石墨烯纳米片@硝酸钠;(b) 石墨烯纳米片质量分数为1.5%的石墨烯纳米片@硝酸钠Fig.7.L-J interaction between atoms in GNS@NaNO3:(a) GNS@NaNO3 when GNS weight concentration is 1.0%;(b) GNS@NaNO3 GNS weight concentration is 1.5%.

也就是说,石墨烯纳米片与硝酸钠熔盐之间存在的相互吸引作用导致了熔盐致密层的形成.而掺杂不同质量分数纳米片的复合材料体系内致密层的厚度不同,这使得二者之间的相互作用强度存在一定的差异,从而导致了复合材料相变焓不同程度的降低.

与此同时,本文计算了复合体系内石墨烯纳米片与硝酸钠之间的相互作用能.相互作用能常用于表征材料间的相互吸引或排斥的强度,仅与材料的本征特性相关.计算公式[27]如下所示:

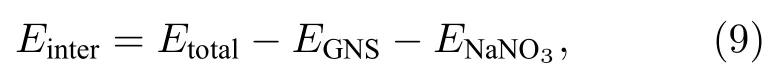
式中Etotal代表模拟体系的总势能,EGNS和ENaNO3分别代表石墨烯纳米片和硝酸钠的势能.从图8 可以看出,石墨烯纳米片与硝酸钠之间存在较强的相互吸引作用且随着石墨烯纳米片质量分数的增加,纳米片与硝酸钠之间相互作用能的变化趋势与相变焓恰恰相反.在纳米片质量分数为1.0%时二者之间的相互吸引作用最弱,质量分数为1.5%时相互吸引作用最强.由此可以推断,纳米片与硝酸钠熔盐之间相互作用能的存在及其强弱是复合相变材料相变焓降低的根本原因.

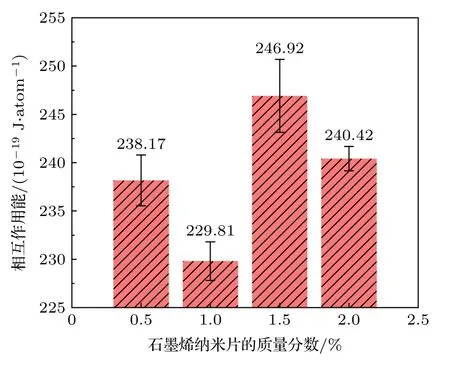
图8 石墨烯纳米片与硝酸钠之间的相互作用能Fig.8.Interaction energy between GNS and NaNO3.

5 结论

本文制备了质量分数分别为0%,0.5%,1%,1.5%,2%的石墨烯纳米片@硝酸钠复合相变材料,采用SEM 对复合材料进行表征,并通过DSC 测试得到了复合材料的熔点及相变焓.开展分子动力学模拟并分析了掺杂石墨烯纳米片对复合相变材料相变热特性的影响机理和作用规律,主要结论如下:

1)石墨烯纳米片附近存在团簇状的硝酸钠熔盐,且随着纳米片质量分数的增加,石墨烯纳米片@硝酸钠复合相变材料的熔点略有下降,相变焓呈现非依数性降低.纳米片质量分数为1.5%时下降最为明显,仅为理论相变焓的86.19%.这说明团簇在纳米片附近的熔盐致密层未发生熔化.

2)石墨烯纳米片的引入削弱了硝酸钠内部分子间的相互作用,体系内硝酸钠分子无规则运动加剧,平均自由程增大,原子迁移率增高,分子间碰撞频率增大,从而降低了其熔点.纳米片与硝酸钠之间较强的范德瓦耳斯吸引作用是纳米片附近2—4 Å的熔盐致密层形成的根本原因.且随着石墨烯纳米片质量分数的增加,熔盐致密层与石墨烯纳米片之间的质心等效距离逐渐增大,二者之间的相互吸引作用呈现先增强后减弱的趋势.在纳米片质量分数为1.5%时二者间的质心等效距离最接近势阱位置,相互吸引作用最强,熔盐分子的运动受限最为严重,因此复合材料的相变焓降低最为明显.

3)基于以上两点结论,熔盐与纳米增强剂之间的相互作用类型及其势阱位置是决定复合后熔盐致密层厚度及相变焓降低程度的根本原因,可借助相互作用能的计算指导纳米增强剂的掺杂比选择,最大程度避免纳米增强剂的引入造成的芯材团簇和相变焓损失,同时一定程度上减少复合相变材料的制备成本.