用于等离子体相干模式自动识别的谱聚类算法实现

赵子博 庄革 谢锦林 渠承明 强子薇

(中国科学技术大学核科学技术学院,合肥 230026)

高约束模式对改善等离子体约束有着重要意义,但目前主要依赖人工进行模式识别,其效率低、成本高,导致核聚变装置中大量的诊断数据没有得到充分分析.为了解决这个问题,本文将机器学习中的谱聚类算法应用到EAST 托卡马克装置上的电子回旋辐射成像、一维诊断系统电子回旋辐射计、磁探针、软X 射线和快辐射等不同诊断系统的数据上,在时域及频域上识别出了锯齿模,验证了谱聚类方法的迁移性及准确性,解决了监督学习在数据处理上迁移性差以及需要依赖大量标签数据的问题.此外,本文实现了特定模式的筛选;最后利用电子回旋辐射成像及磁探针数据发现了一种可能的新模式,为新模式探索提供了一种新思路.

1 引言

自1982 年ASDEX 装置第一次获得了高约束模式[1]以来,托卡马克装置的能量约束时间不断提高.由于高约束模式对等离子体具有良好的约束性能,因此被认为是最有可能实现核聚变的运行模式.但同时在高约束情况下存在各种不稳定模式,比如伴随着台基区等离子体约束性能的周期性下降的边界局域模[2];伴随着等离子体芯部密度和温度的周期性耗散的锯齿模[3].为了优化托卡马克的设计以改善等离子体约束,必须要对等离子体中的模式进行识别.

核聚变装置已经积累了大量的诊断数据,例如EAST 托卡马克装置上的电子回旋辐射成像(ECEI)系统自2012 年以来,已经采集超过7000炮,每一炮的数据大小约为7.6 GB,总数据量已超过40 TB[1].此外,诊断系统繁多,比如一维诊断系统电子回旋辐射计(ECE)[4]和 ECEI[5−9]等,因此总数据量巨大.然而目前主要依赖人工进行模式区分,该方法效率低、成本高,无法满足实际需求,导致大量的诊断数据没有得到充分分析.因此寻找高效模式识别的方法十分重要.

近年来,机器学习在核聚变领域已经有了广泛而深入的应用.机器学习分为监督学习与无监督学习,目前在可控核聚变领域应用最多的是监督学习[10−12].但是监督学习在处理数据方面有很大的缺陷,一方面监督学习需要大量带有标签的数据来进行训练,而目前大多数诊断数据的标签尚未完善;另一方面监督学习的迁移性很差,对于不同装置或者同一装置上的不同诊断系统,甚至同一装置上的同一个诊断系统不同条件下的数据都需要重新训练模型,效率低、适用性差.而无监督学习不存在此缺点,因此本文采用无监督学习的方法.

目前无监督学习以聚类算法为主,传统的聚类算法有K均值算法[13]、层次聚类算法以及密度聚类算法.其中,K均值算法对初值敏感,仅适用于凸形簇[14];密度聚类时间复杂度高、效率低,参数选取缺乏理论性;层次聚类算法不能更正错误的决策且偏好凸形簇,且对簇的大小有一定的要求.相比之下,基于图论的谱聚类算法首先具备迁移性强的特点;其次,该算法对样本分布的适应性强[1],可以用来识别各种形状的簇;最后,谱聚类算法对初值不敏感[15,16],且应用该算法可以高效且准确地处理数据[1].

综上,本文主要以谱聚类算法为基本算法,对EAST 托卡马克装置上不同诊断系统包括ECEI、ECE、磁探针、软X 射线(SXR)和快辐射,密度诊断上的数据进行自动处理,实现自动寻找模式的目的,为新模式探索提供一种新思路.同时还能实现特定模式的筛选,大幅减少研究人员用于数据处理上的时间.

2 谱聚类算法实现

2.1 类别数已知情况下算法原理

聚类算法的任务是基于数据间的关系将不同的样本划分成多个不相交子集.谱聚类算法将样本看成空间的点,每两个点之间用一条被赋予权值的边连接.每条边的权值表示样本之间的相似度,权值越大,相似度越强.通过对该图的划分,使各个子图内部边权的和越大越好,不同子图间边权的和越小越好,进而实现聚类的目的[1].假设N个样本,K个类别,定义损失函数为[9]

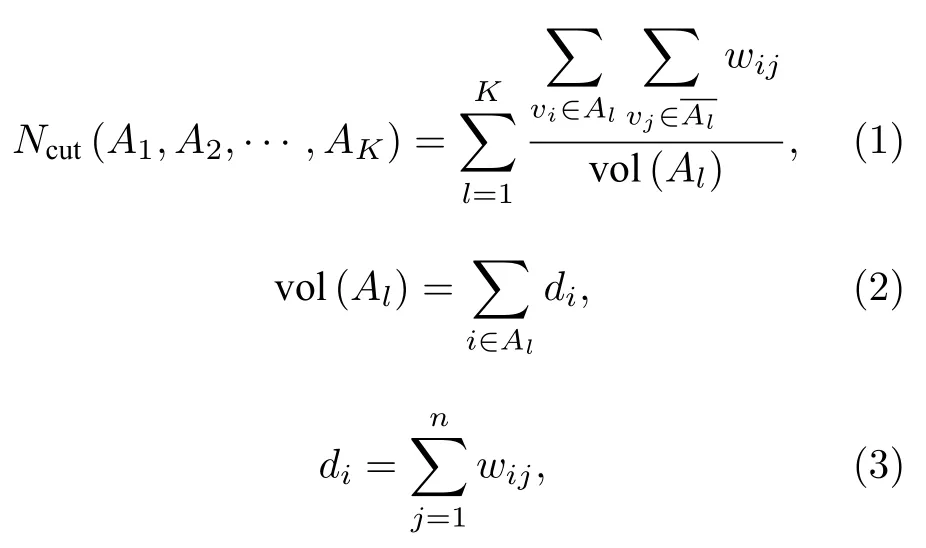
其中wij表示第i个点与第j个点之间的相似度,Aj表示第j个类别,vi表示第i个样本,di表示所有样本与第i个样本之间的相似度的总和,vol(Al) 表示属于该类别的样本与所有样本之间相似度的总和.

损失函数最小对应于最合理的分类标准.但是由于寻找损失函数最小值是一个无法在多项式时间内计算求解的问题(NP 难问题),因此要寻找一种近似算法使其在有限的计算资源和时间下可以求解.首先,将损失函数改写为矩阵形式:

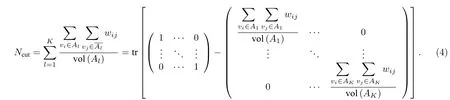
进一步,定义矩阵:

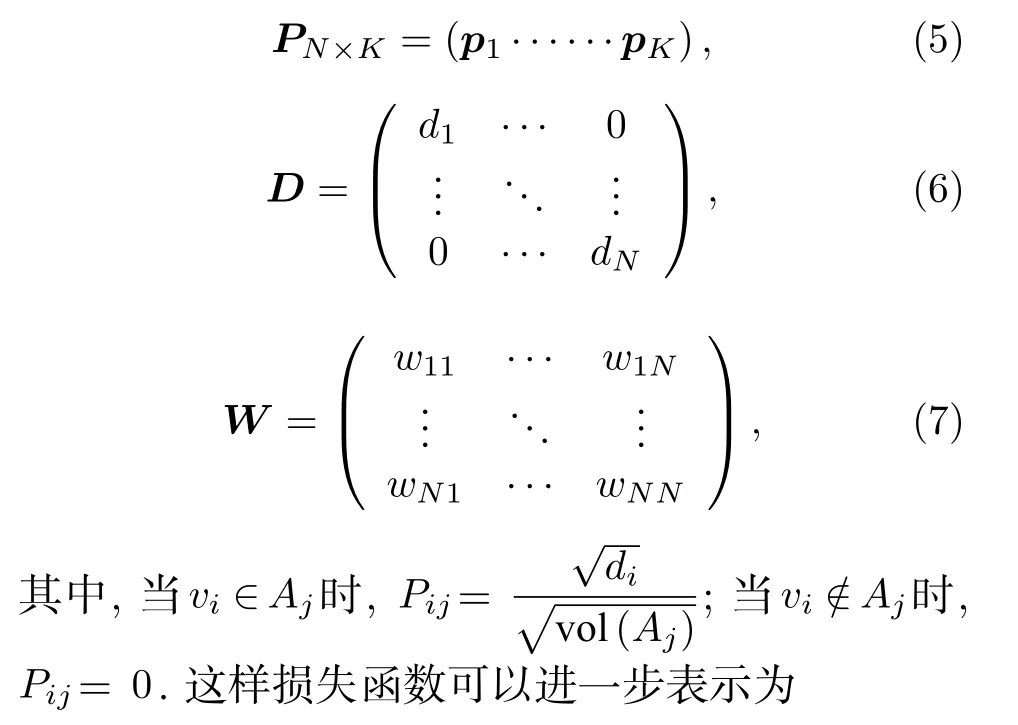
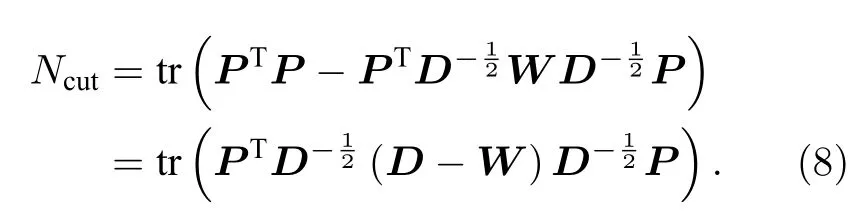
定义

求解损失函数最小值,即为求解 tr(PTV P)在PTP为单位矩阵条件下的最大值.对于这类条件极值问题,类似主成分分析,可以运用拉格朗日乘子法进行求解,即

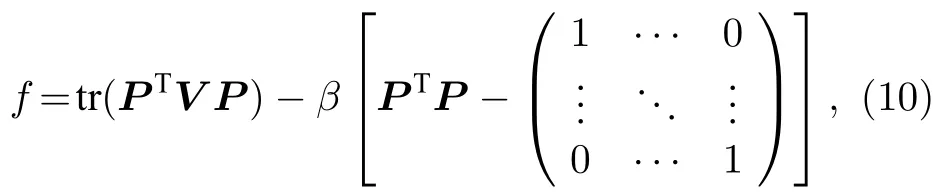
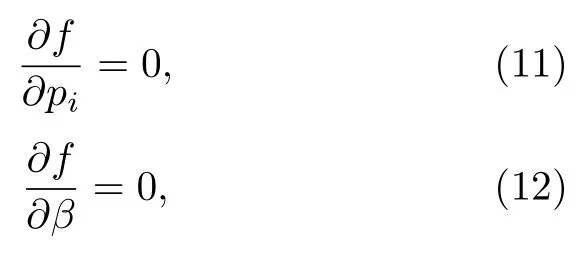
其中β是待定常数.通过(11)式和(12)可以得到

求解该特征方程可以得到N个特征值,即β的N个取值.其中最大的K个特征值的和就是损失函数的最大值,即

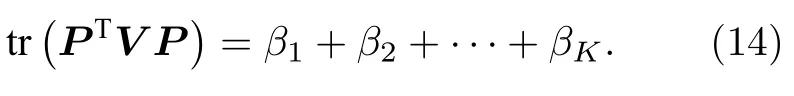
将选取的特征值所对应的特征向量组合构成P矩阵.令P矩阵的K个列向量组成K维子空间.根据P矩阵的定义,P矩阵包含着分类信息,每个行向量与一个样本对应,同类样本趋于K维子空间的一个轴分布,不同类样本会在不同轴上分布.计算每个样本(P矩阵的每个行向量)到每个类别聚类中心的距离,用 (vj,ci)dist来表示第j个样本与第i个聚类中心间的距离,

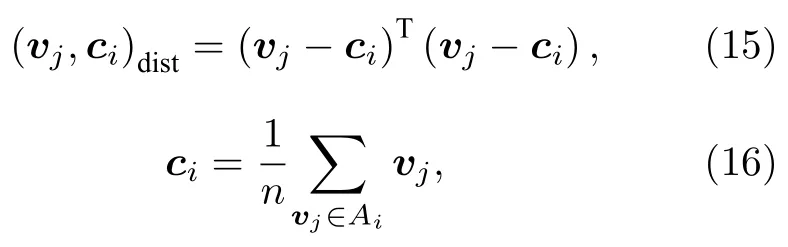
其中,vj表示第j个样本,ci表示第i个类别的聚类中心,n表示属于第i类的样本数.将该样本划分到与它距离最小的聚类中心所代表的类别中,所有样本分配完毕后,重新计算聚类中心.如果聚类中心发生变化,重新分配样本直到聚类中心不再发生变化为止.值得注意的是,以上过程体现了谱聚类算法的两个优势,其中一个优势是将原本复杂的样本结构转换成了简单的分布(同类样本在坐标系中的一条直线上分布,不同类样本在不同直线上分布),便于分类,因此保证了算法的准确性;另一个优势是将原本高维的样本数据进行了降维(P矩阵的每个行向量的维度是类别数),提高了算法的效率.

2.2 类别数未知情况下算法原理

在实际工作中,多数情况下类别数不能事先确定,因此需要一个方法自动确定类别数.定义第j个样本与第i个聚类中心间的距离为

其中

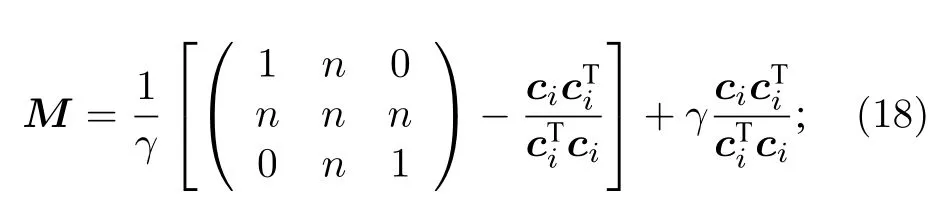
ε为一个很小的数,取为eps,即ε=2.2204×10–16;γ用来控制簇的粗细,γ越小,分类标准越高,通常取0.01.

按上述定义距离的方法,可以使得同种类别(径向分布)样本之间的距离小于样本到坐标原点的距离,不同种类样本之间的距离大于样本到坐标原点的距离[1].因此,在最开始进行分类的时候,可以假定样本会被分成3 类,其中2 个类别的聚类中心分别由样本间相似度最低的2 个样本定义(确保2 个样本不是同一类);第3 个类别的聚类中心为坐标原点.之后,计算每个样本分别到3 个聚类中心的距离,将样本划分到与它距离最小的聚类中心所代表的类别中.所有样本划分完成后,更新聚类中心,循环迭代,直到聚类中心不再变化为止.完成后,如果原点所代表的类别中没有样本,则分类完成,类别数为两类;如果有样本,说明类别数不止两类,需要将类别数调整为4,重复上述过程,直到K+1 类时,原点所代表的类别里无样本,则分类完成,类别数为K.

2.3 算法实现流程

根据2.1 节和2.2 节的分析,谱聚类算法的基本流程为图1 所示.

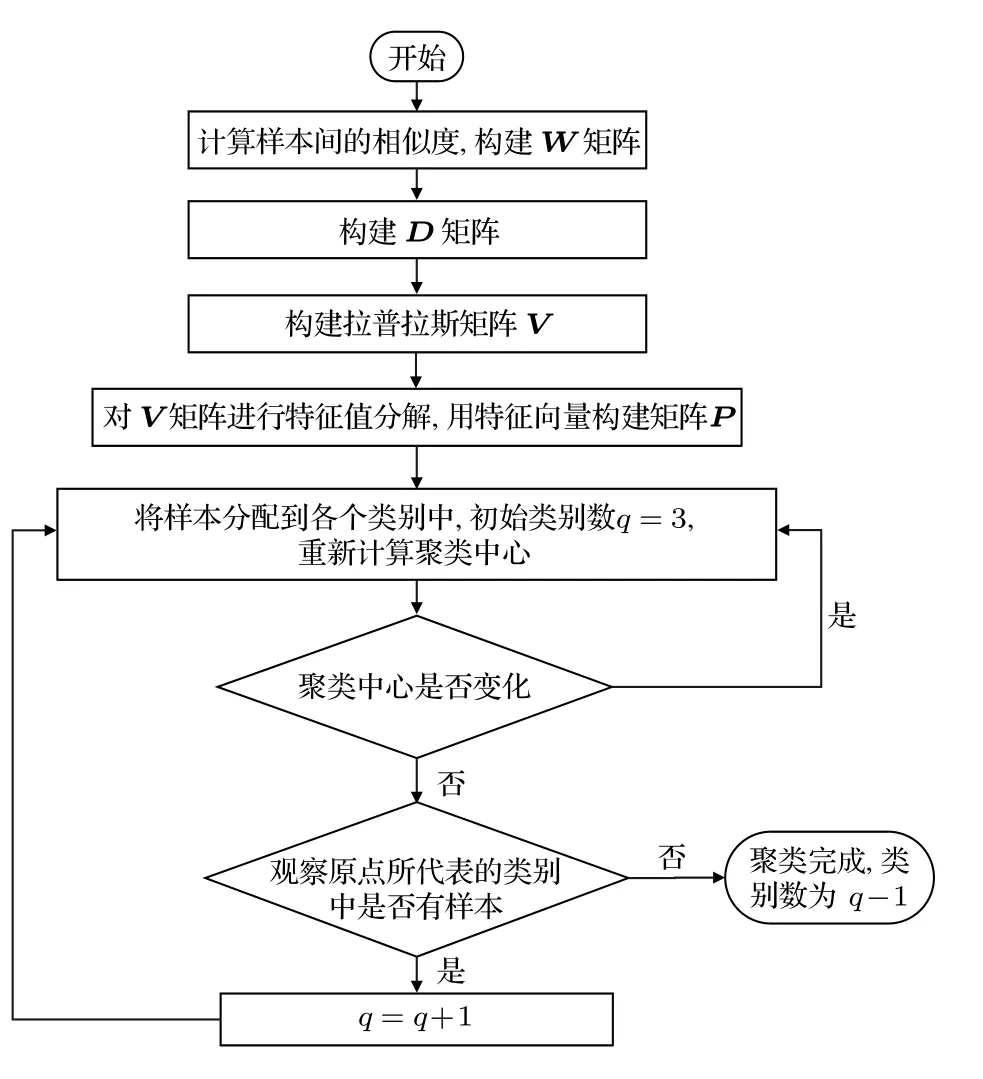
图1 谱聚类算法流程图Fig.1.Flow chart of spectral clustering algorithm.

3 等离子体相干模式识别及特定模式筛选

3.1 多维诊断数据空间聚类

为了对等离子体模式的空间特征进行更好的研究,发展出了大量的多维诊断系统,比如ECEI和SXR 成像阵列等.多维诊断系统可以给出空间各点的信息,因此可以利用空间聚类的方法对空间各点进行分类,每一种类别对应一种模式,以此来寻找其中的模式.本文以ECEI 诊断数据识别为例进行说明.

EAST 托卡马克装置上的ECEI 诊断系统有24 行、16 列独立的数据信道[17−19].每个数据信道对应一个样本,总共有384 个样本.每一个样本是一个时间序列,两个样本之间的相似度为

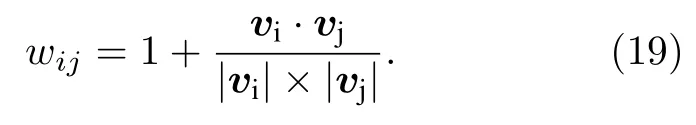
采取这种定义方式是因为同一类别(模式)的表现形式是数据随时间的变化规律相同,但幅值可以不同.余弦距离关注方向上的变化,不关注幅值,采取余弦距离定义相似度正好符合这个表现形式.之后按图1 所示的操作流程对ECEI 数据每隔0.1 s进行一次聚类识别.在42987 炮1.3—9.4 s 内识别出的模式如图2 所示,每个方格对应一个ECEI 的信道,总共384 个;白色与黑色各代表1 种类别.

图2 聚类识别分类结果Fig.2.Cluster recognition classification results.

为了证明所识别出来的确实是一种模式,现在以4.0—4.1 s 为例对其进行物理上的一些分析.首先从白色区域选出一个信道A (第12 行,第9 列),再从黑色区域选出一个信道C (第2 行,第4 列),最后在白色区域与黑色区域交界处选出一个信道B (第20 行,第9 列)画出时序图,如图3 所示,其中,δTe/Te(Te−〈Te〉)/〈Te〉,Te代表对应时刻的电子温度,〈Te〉为4—4.1 s 内电子温度的平均值.可知信道A 与信道C 信号明显分为爬升期、先兆振荡期和快速崩塌期3 个阶段,符合锯齿模[5,20,21]的基本特征,因此可以判断出A 通道信号为正锯齿,C 通道信号为反锯齿;交界处B 通道信号温度保持不变,为反转半径位置.正锯齿和反锯齿的同时存在可以视为判断锯齿不稳定性的简单依据[5].

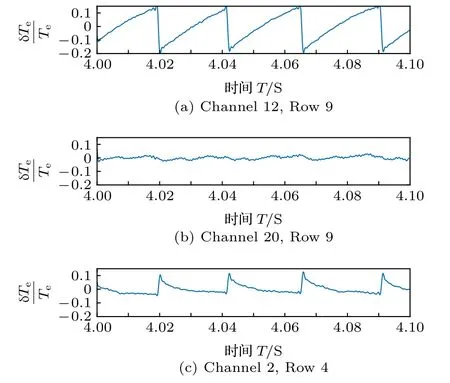
图3 各信道的信号时序图 (a) 信道A;(b) 信道B;(c) 信道CFig.3.Signal timing diagram of the different channel:(a) Channel A;(b) channel B;(c) channel C.

图4 给出了ECEI 观测到的锯齿不稳定性演化过程图,标号(1)—(8) 依次对应8 个时刻点;图4(b)黑色、红色、蓝色曲线分别代表图4(a)各图对应颜色点处的时序图.从图4(b)可以明显看出:最开始锯齿崩塌结束,冷磁岛占据整个q=1 面;随着等离子体加热,锯齿爬升,芯部电子温度缓慢提高,之后重联发生,芯部热量向外输运;最后锯齿崩塌,冷磁岛重新占据整个q=1 面,符合锯齿模的演化过程.从图4(a)可以看出,整个演化图的空间结构与利用谱聚类的方法识别出的模式空间结构基本一致,说明识别出的白色区域对应反转半径以内的区域,为正锯齿;黑色区域对应反转半径与混合半径之间的区域,为反锯齿,证明了谱聚类方法的可靠性.

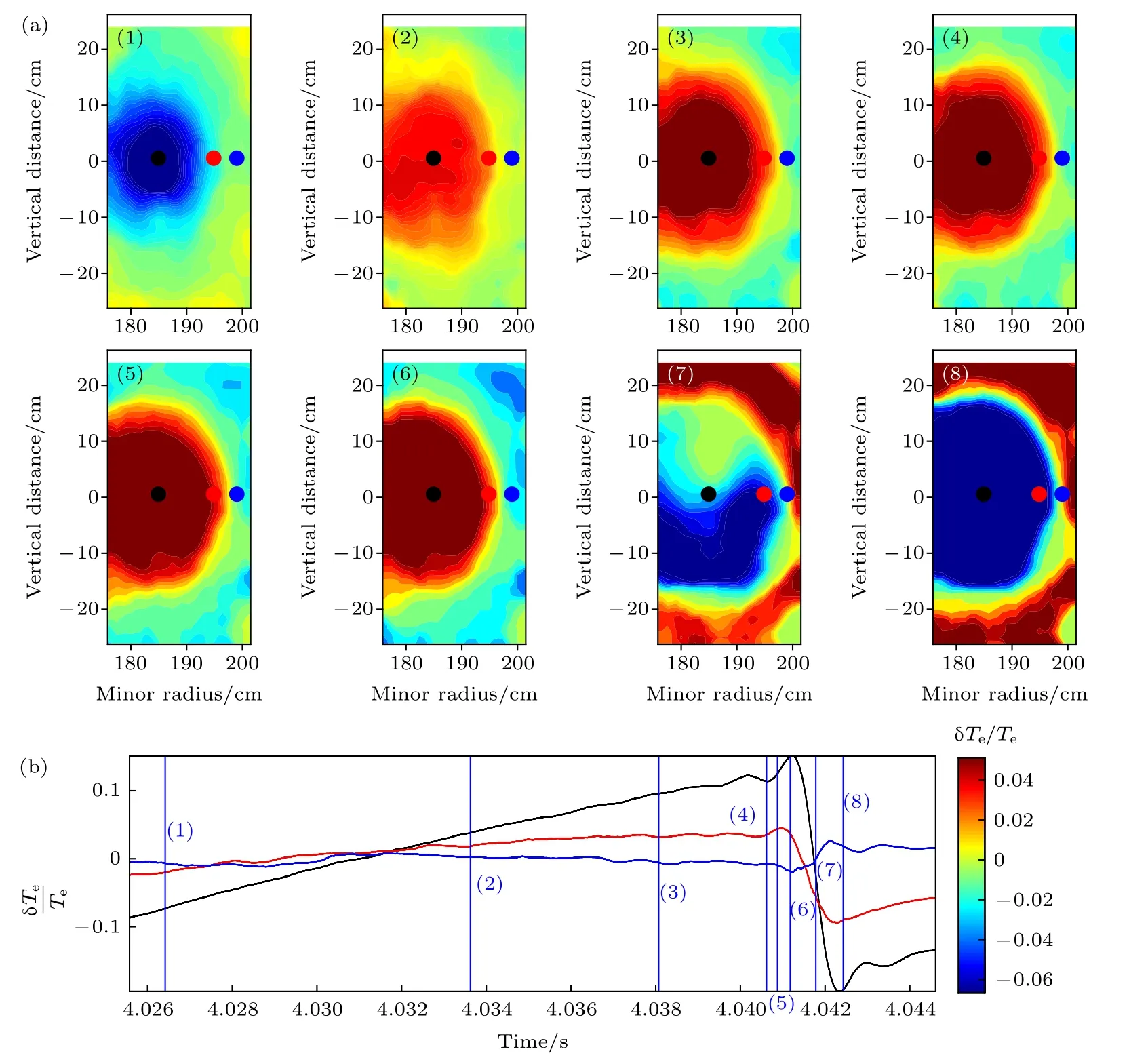
图4 (a)锯齿模空间结构随时间的演化过程;(b) 黑色、红色、蓝色曲线分别代表图4(a)各图对应颜色点处的时序图Fig.4.(a) Evolution of the space structure of sawtooth mode with time;(b) the black,red,and blue curves respectively represent the timing diagrams at the corresponding color points of each panel in Fig.4(a).

用查准率P和查全率R来衡量算法的准确性,定义为

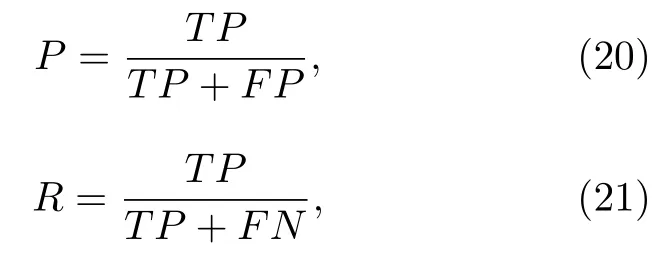
其中,TP表示真正例,FN表示假反例,FP表示假正例.TP指真实情况和识别结果均为正例;FP指识别结果为正例,但真实结果为反例;FN指识别结果为反例,但真实结果为正例.对所有的识别结果进行统计,在42987 炮的38400 个时间片段(384 个信道,每隔0.1 s 聚类一次,数据采集时间10 s)内,聚类的结果显示共有13041 个时间片段被识别为正锯齿,共有9558 个时间片段被识别为反锯齿.通过测量的信号时序图,可以判定实际存在正锯齿的时间片段共有12555 个,实际存在反锯齿的时间片段共有9234 个.此外,可以判定在聚类算法识别判定为正锯齿的13041 个时间片段中共有12150 个片段是真实的正锯齿,在聚类算法识别判定为反锯齿的9558 个时间片段中共有8829个片段是真实的反锯齿.根据查准率与查全率的定义,可以计算得到正锯齿的查全率为96.8%,查准率为93.2%;反锯齿的查全率为95.6%,查准率为92.4%.以上结果表明,谱聚类算法在识别准确性上表现良好.

3.2 一维诊断数据时间聚类

在核聚变装置上除了多维诊断系统,还存在大量一维诊断系统,包括ECE、磁探针、弦积分密度测量、SXR 以及快辐射等.一维诊断数据通常反映空间单点或者单通道的信息,相比多维诊断系统,一维诊断系统可供分类的信息更少,可以利用时间聚类来自动识别其中的相干模式.下面以ECE 诊断系统为例进行具体说明.

对ECE 诊断的时序信号进行傅里叶变换,得到各个时间点的频率信息,每个时间点的频率序列对应一个样本,同种模式的表现特征是频率序列强度相似.各个样本的相似度用样本之间的指数距离表示为

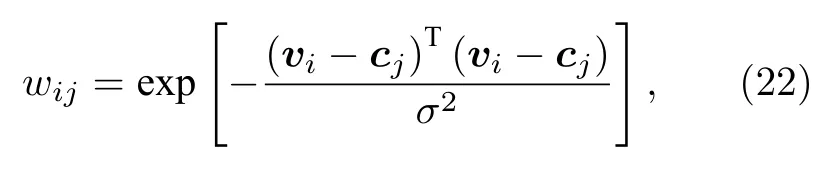
其中σ为人为规定的参数,用来控制样本间的相似度,本文中σ2=1000.

对数据每隔0.1 s 识别一次,在50015 炮的1.8—9.5 s 内发现了一种模式,图5 为该模式的频谱图.通过频谱图,可以发现有展宽非常大的破裂,符合锯齿模的特征,认定识别出的模式为锯齿模.对于SXR、快辐射以及ECE 三种诊断数据仿照前述操作进行时间聚类,对50015—50115 炮的24000 个时间片段的识别结果进行统计,其中6700 个时间片段被识别为锯齿模.根据频谱图,可以判定有6555 个真实存在锯齿模的时间片段.同时,根据频谱图也可以判定出在被聚类算法识别出的6700 个锯齿模片段中,有6057 个是真实的锯齿模片段.因此,根据(20)式和(21)式对查准率和查全率的定义,可以计算得到P=90.4%,R=92.4%.

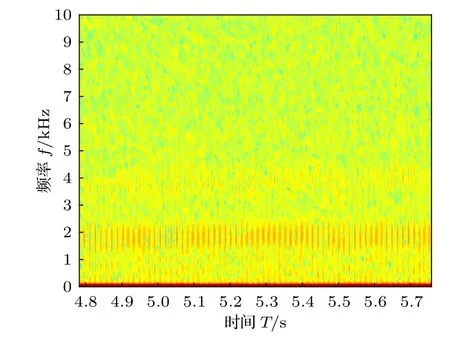
图5 对于50015 炮,模式频率特征Fig.5.Mode frequency characteristics for shot 50015.

为了实现自动筛选模式,将聚类识别找到的在50015 炮1.8—9.5 s 内的锯齿模的典型信号,即聚类中心提取出来加到时间聚类的样本里,并作为初始聚类中心.在识别过程中,与该序列分在一类的便是该种模式,以此达到筛选特定模式的功能.对42987—50180 炮内的480000 个时间片段进行筛选识别,其中10730 个时间片段被识别为锯齿模.根据频谱图,可以判定有10719 个真实存在锯齿模的时间片段;同时,根据频谱图也可以判定出在被聚类算法识别出的10730 个锯齿模片段中有10708 个是真实的锯齿模片段.因此,根据(20)式和(21)式,可以计算得到查准率为99.8%,查全率为99.9%.证明谱聚类算法在模式筛选上的表现非常好,可以实现筛选特定模式的功能,大幅减少研究人员的时间.

3.3 新模式探索

仿照前述锯齿模的识别方法,利用ECEI 数据在64960 炮3.3—3.6 s 内发现了一种模式,见图6.图6(a)中每个方格对应一个信道,总共有384 个;对384 个样本进行空间聚类,识别出了一种模式,用浅蓝色方格表示.图6(b)是通过时域图及频谱图判断出的该模式实际出现的位置,蓝色方格区代表模式出现的地方.两者对比,发现聚类识别出的结果与模式实际出现的位置基本吻合.图6(c)反映该模式在托卡马克装置中的实际位置,其中黑色方格区即为图6(b)在托卡马克装置中的实际位置.EFIT 代表磁面,信号代表模式,本底代表无模式的地方,饱和代表测量的数据超量程的地方,干扰代表噪声.图7 为该模式的频谱图,可以清晰地看到,这种模式的频率范围在80—120 kHz 之间.

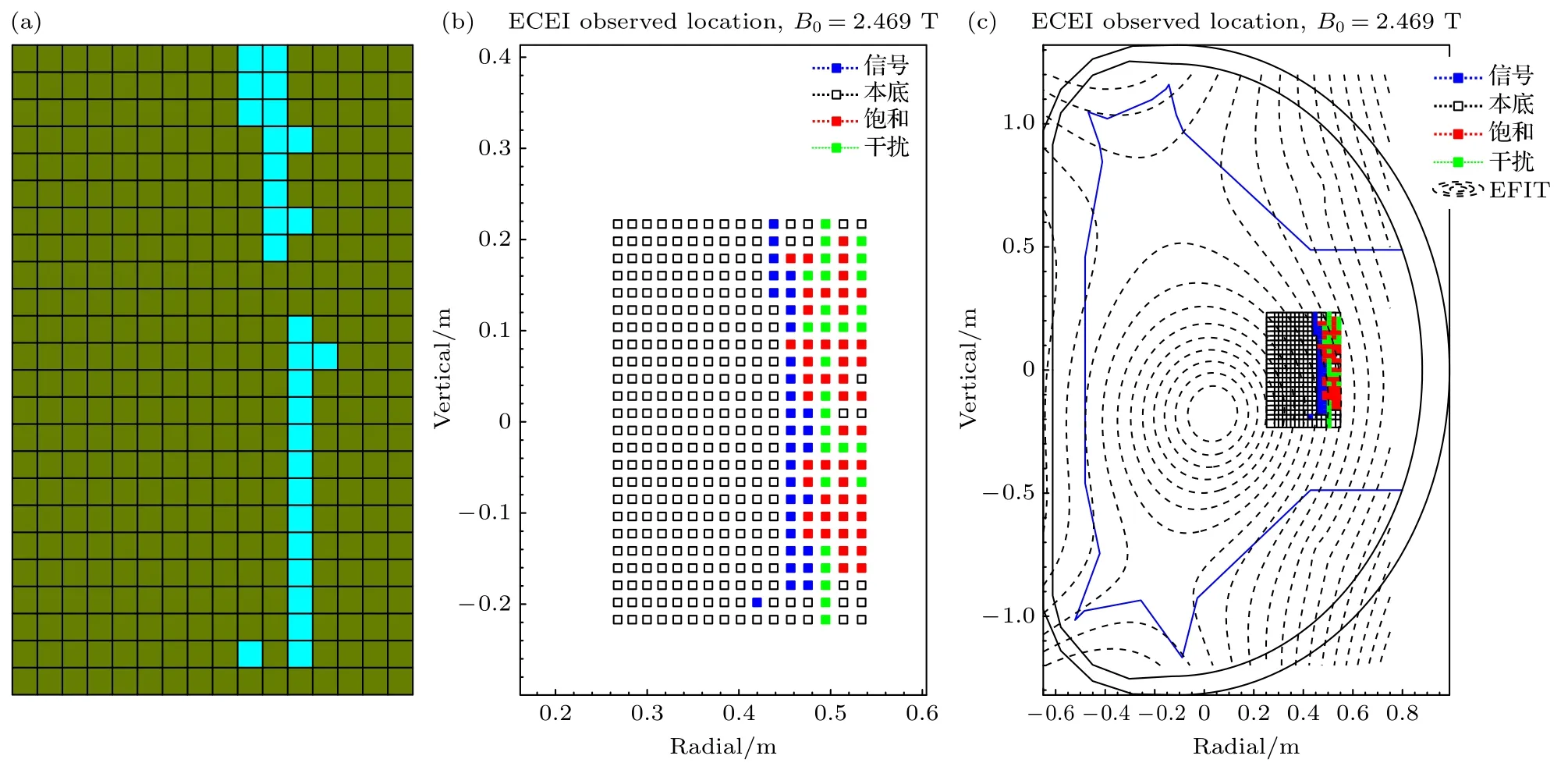
图6 聚类识别结果以及模式实际观测到的位置 (a) 聚类识别结果;(b) 模式实际出现的位置;(c) 模式在托卡马克中的位置Fig.6.Cluster recognition results and the position where the pattern is actually observed:(a) Cluster recognition results;(b) the position where the pattern actually appears;(c) the position of the pattern in the Tokamak.

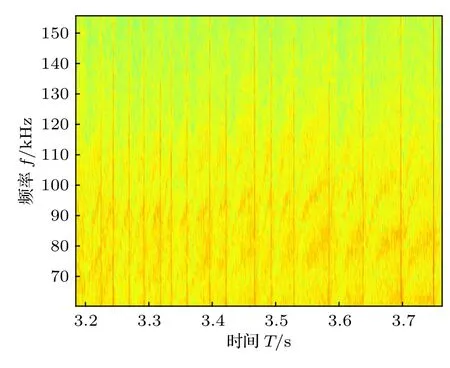
图7 对于64960 炮,模式频率特征Fig.7.Mode frequency characteristics for shot 64960.

利用64960 炮识别出的该模式的典型信号进行模式筛选,在64962,64964,64965,64966,64967,64968,64969 炮也同样发现了该模式.可以发现该模式存在于ECEI 第5 列附近,空间分布有一定特点;在频谱图上也具有一定特点.目前,还没有对此类模式的记载,由此可以推断模式很可能是一种新模式.值得注意的是,对于该模式的判定,以及它是否为新模式,仍需进一步物理上的分析.但谱聚类方法给出了一种寻找潜在的新模式的新思路,这在模式识别上具有很高的应用价值.

4 结论

本文利用谱聚类的方法对EAST 装置上不同诊断系统的数据,包括ECEI、ECE、磁探针、SXR以及快辐射数据进行了分析,在识别精度以及效率方面表现良好.尤其可以对特定模式进行筛选,具有较大的实用性;此外填补了谱聚类算法在单点一维数据识别上的空白.由于在识别不同数据及不同模式时,算法本身不需要进行调整,因此表明其优异的迁移性,为实际工作带来了便利.利用谱聚类算法能为寻找潜在的新模式提供新思路,对等离子体物理的研究有很大的意义.目前定义数据之间的相似度使用的是距离度量方式,为进一步提高识别精度以及效率,下一步将会寻找更适合核聚变装置数据的相似度度量方式.