基于连续近似的轨道共线公交线路优化模型
刘 媛 罗孝羚
(重庆交通大学交通运输学院, 重庆 400074)(重庆交通大学重庆市交通运输工程重点实验室, 重庆 400074)
近年来,轨道交通的发展极大改善了当前城市交通拥堵情况,丰富了乘客的出行方式.然而,轨道交通站点位置选择没有充分考虑公交与轨道交通的衔接关系,导致轨道交通建成后出现原有公交线路布设不合理、部分乘客采用公交接驳轨道交通的换乘时间过长等一系列问题.建成后的轨道交通站点具有不可调整性.因此,对于已经建成的轨道交通线路,如何调整与其共线的公交线路,成为现在城市公交优化尚需探索的新问题.
目前,针对公交线路优化问题的研究中,根据优化变量是否连续可以分为离散模型和连续模型2类.文献[1-6]针对不同需求场景,采用离散决策变量研究公交线路优化方法;文献[7-10]对离散模型的算法进行了探讨;文献[11-12]采用连续变量,分析连续公交线路优化模型;文献[13-17]根据不同场景,对现有的连续模型进行拓展.与离散模型相比,连续模型优化变量较少,故能够获得解析解.然而,上述研究都侧重于探讨公交线路的优化设计方法,没有考虑新建轨道交通对于公交的影响.文献[18]指出,轨道交通的引入会对原有的公交线路产生重要影响,需要有效协调2种交通方式的关联关系,才能使公交系统高效运营.文献[19]结合实际规划设计需要,提出了轨道共线段公交发车班次的优化方法;文献[20]研究了轨道交通共线的公交支线设计方法;文献[21-22]分析了多种交通工具的公交线路设计方法.但这些模型均采用离散变量,导致模型求解困难且解的质量不高.
针对离散模型存在的问题,本文使用连续变量,构建了与轨道交通共线的公交线路优化模型,继而提出相应的求解算法.
1 公交站点优化模型
1.1 连续近似方法
确定公交站点位置的连续近似方法[23-26]是根据微积分的思想,将离散的站点位置用连续的站点密度来表示,从而将离散模型转化为连续模型.获得站点密度解后,采用积分法将公交站点的密度转化为公交站点的具体位置.对公交站点密度进行积分时,若每次积分获得一个整数,则在积分区间布设一个公交站点(见图1).图中,δ(x)*为站点密度;R1和R2为积分整数区间的端点;R为线路区间终端点.积分区间的端点或中点即为所得站点位置,对应方法分别为端点法和中点法.文献[27]指出,采用中点法和端点法所得到的系统总成本相近.
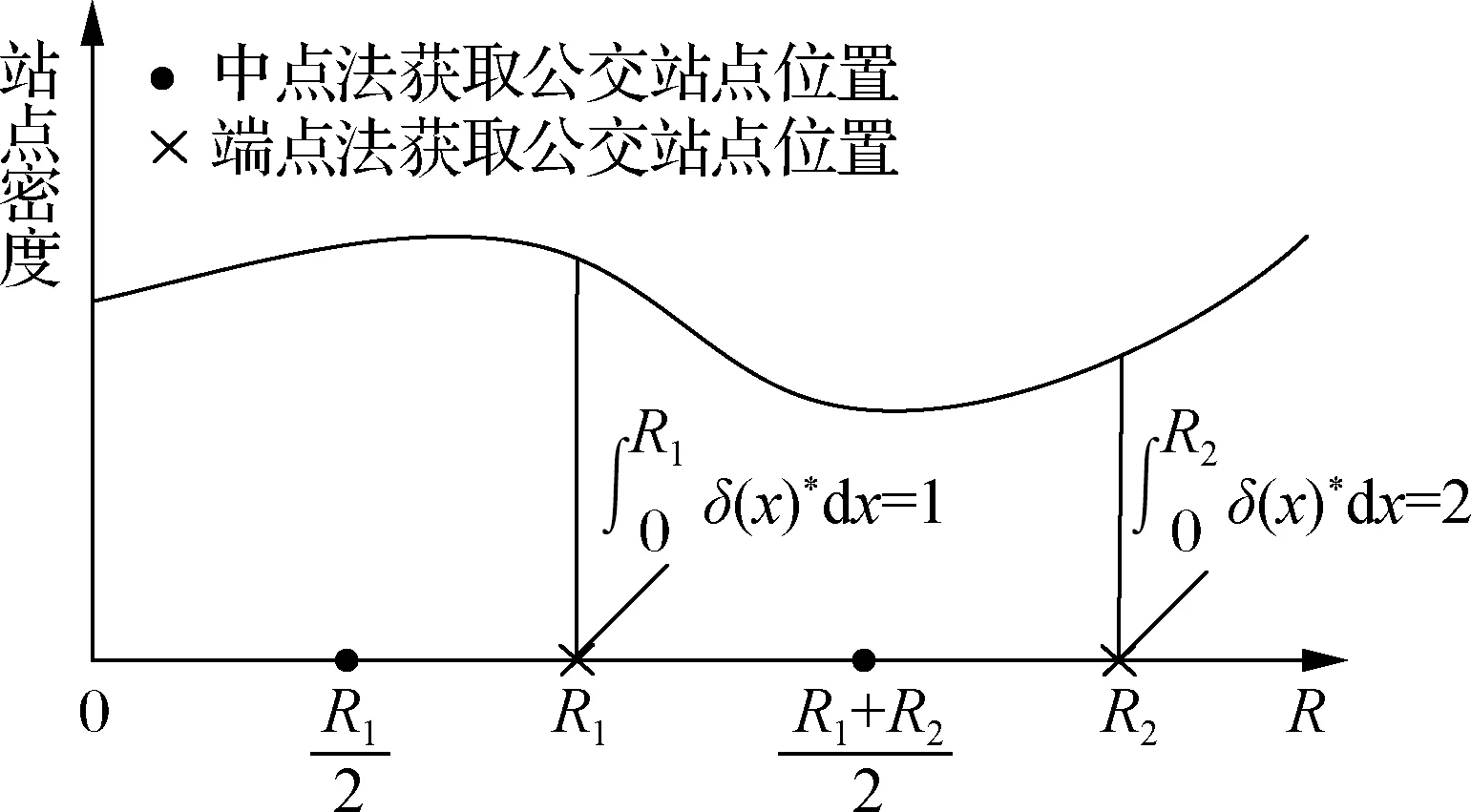
图1 公交站点位置确定方法示意图
1.2 模型假设
为了便于模型的建立,首先进行如下假设:
1) 乘客以出行时间最小化为目标,选择相应的出行路径.乘客在出行过程中,可以选择单一交通方式的路径,也可以选择组合交通方式路径.组合交通方式包括公交换乘轨道、轨道换乘公交以及公交换乘轨道再换乘公交.
2) 优化区域内的公交客流是外生的,即客流不随公交系统设计的变动而变化.
3) 优化区域内均能布设公交站点.但在实际优化中,站点位置可以根据实际需求进行调整[28].
1.3 轨道交通共线公交线路优化模型
1.3.1 目标函数
公交线路的优化目标为系统总成本最小.公交系统总成本包括运营成本和乘客出行时间成本2个部分,其目标函数可表示为
(1)
式中,Z为系统总成本;Co为运营成本;Cp为乘客出行时间成本;μ为时间价值系数,用于将运营成本转化为时间成本.
公交系统的运营成本可细分为基于运营时间的运营成本Ct、基于运营里程的运营成本Cl以及站点设施设备建设和维护成本Cs.以单方向的公交运营为例,各成本项可分别表示为
(2)
(3)
(4)
式中,πt、πl、πs分别为单位时间运营成本系数、单位里程运营成本系数和单个站点建设及维护成本系数;hb和δb(x)分别为发车间隔和位置x处的公交站点密度;L为线路总长度;Vb(x)为位置x处考虑站点延误的公交运行速度,且
(5)
式中,τ0、τb、τa分别为公交车辆的站点固定停靠时间、乘客平均上车和下车时间;vb为公交行驶速度;Bb(x)和Ab(x)分别为位置x处的公交上车密度和下车密度.
乘客出行时间成本可细分为步行时间成本Ca、等待时间成本Cw、在车旅行时间成本Cv以及换乘惩罚时间成本Cf.乘客可以选择公交或轨道出行,定义m为乘客交通方式的选择标识,r和b分别为轨道和公交选择标识,即m∈{r,b},各成本项可分别表示为

(6)
(7)
(8)
(9)
式中,bm(x)和am(x)分别为位置x处不考虑换乘的交通方式m的乘客上车密度和下车密度;λr-b(x)和λb-r(x)分别为位置x处从轨道交通换乘至公交和从公交换乘至轨道交通的客流密度;κm(x)为位置x处交通方式m的到站或离站时间;κζ(x)为位置x处乘客的换乘时间;Bm(x)为位置x处交通方式m的乘客上车密度;hm为交通方式m的发车间隔;om(x)为位置x处交通方式m的在车客流量;Vm(x)为位置x处考虑站点延误的交通方式m的运行速度;ξ为换乘惩罚系数.
根据假设条件,乘客总是选择出行时间最短的路径.定义I为乘客出行路径标识,且I∈{r1,b1,br,rb,brb}.其中,r1、b1分别表示仅采用轨道或公交的出行路径;br、rb、brb分别表示采用公交接驳轨道、轨道接驳公交以及公交接驳轨道再接驳公交的出行路径.
对于采用公交出行的乘客,出行时间包含步行时间、等待时间和在车旅行时间,可表示为
(10)
式中,Tb1(x,y)为从位置x处到位置y处采用公交出行的时间;κb(x)、κb(y)分别为乘客从起点到公交站点的步行时间和从公交站点到最终目的地的步行时间;Vb(u)为位置u处考虑站点延误的公交运行速度.
出行路径除了包含2种交通方式的出行时间外,还包括换乘时间和换乘惩罚时间.如采用公交接驳轨道交通,乘客出行时间可表示为
(11)
式中,Tbr(x,y)为乘客从位置x处到位置y处采用公交换乘轨道交通的出行时间;hr为轨道交通发车间隔;Vr(u) 为位置u处考虑站点延误的轨道交通运行速度.
1.3.2 模型约束条件
模型约束条件包括公交发车间隔约束和车辆载客能力约束,可表示为
(12)
max(ob(x))hb≤Kb
(13)

1.3.3 客流分配
根据假设条件,乘客总是选择出行时间最小的出行方式.因此,不同出行路径的客流可表示为
λI(x,y)∈λ(x,y)
TI(x,y)=min{Tr1(x,y),Tb1(x,y),Tbr(x,y),
Trb(x,y),Tbrb(x,y)}
(14)
式中,λ(x,y)为位置x处到位置y处的客流密度;λI(x,y)、TI(x,y)分别为位置x处到位置y处选择路径I的客流密度和出行时间;Tr1(x,y)、Trb(x,y)、Tbrb(x,y)分别为从位置x处到位置y处选择路径r1、rb和brb的出行时间.
2 模型求解算法
2.1 解析解推导
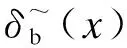

(15)
(16)

考虑约束条件(12)和(13),参考文献[27],可得最优解为
(17)
(18)
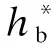
2.2 迭代求解算法
获得解析解的表达式后,设计了一种迭代求解算法,以获得相应的数值解.其中,上层决策优化变量,下层决策客流分配.模型的求解步骤如下:
① 依据约束条件,设置初始解和初始分配的客流.
② 根据式(17),更新站点密度的数值解.
③ 根据式(18),更新发车间隔的数值解.
④ 判断所更新的发车间隔和站点密度是否已经收敛(即发车间隔和站点密度的迭代误差和小于设定值ε),如果已经收敛则转入步骤⑤,否则转步骤②.
⑤ 根据发车间隔和站点密度,更新分配结果.
⑥ 迭代收敛性检查.如果已经达到整个问题的收敛条件,即更新分配结果前后的发车间隔和站点密度的迭代误差和小于设定值ε,则输出结果,否则转步骤②.
3 算例分析
以如图2所示的重庆3#轨道交通线路及与之共线的公交349路所构成的公交走廊为例,对共线的公交站点位置和公交线路的发车频率进行优化.重庆3#轨道线路总长约为67 km,包含45个轨道站点;重庆349路公交线路总长约为17 km,包含26个公交站点;轨道交通和公交线路共线路段约为8 km.案例中共线段公交站点及轨道站点的分布见图2.与轨道交通共线的公交线路可能包含多条,但对于公交走廊而言,多条公交线路服务等价于发车频率增加的单条公交线路服务.因此,案例中仅以一条公交线路为例,对所提方法进行验证.

图2 现有3#轨道交通线路与349路公交站点分布图
根据共线路段的早高峰离散客流,拟合连续客流密度,结果见图3.拟合方法是根据站间距离,将基于站点的客流转化为基于位置的客流密度,然后采用面拟合工具,将离散的客流拟合为连续光滑的密度曲面.
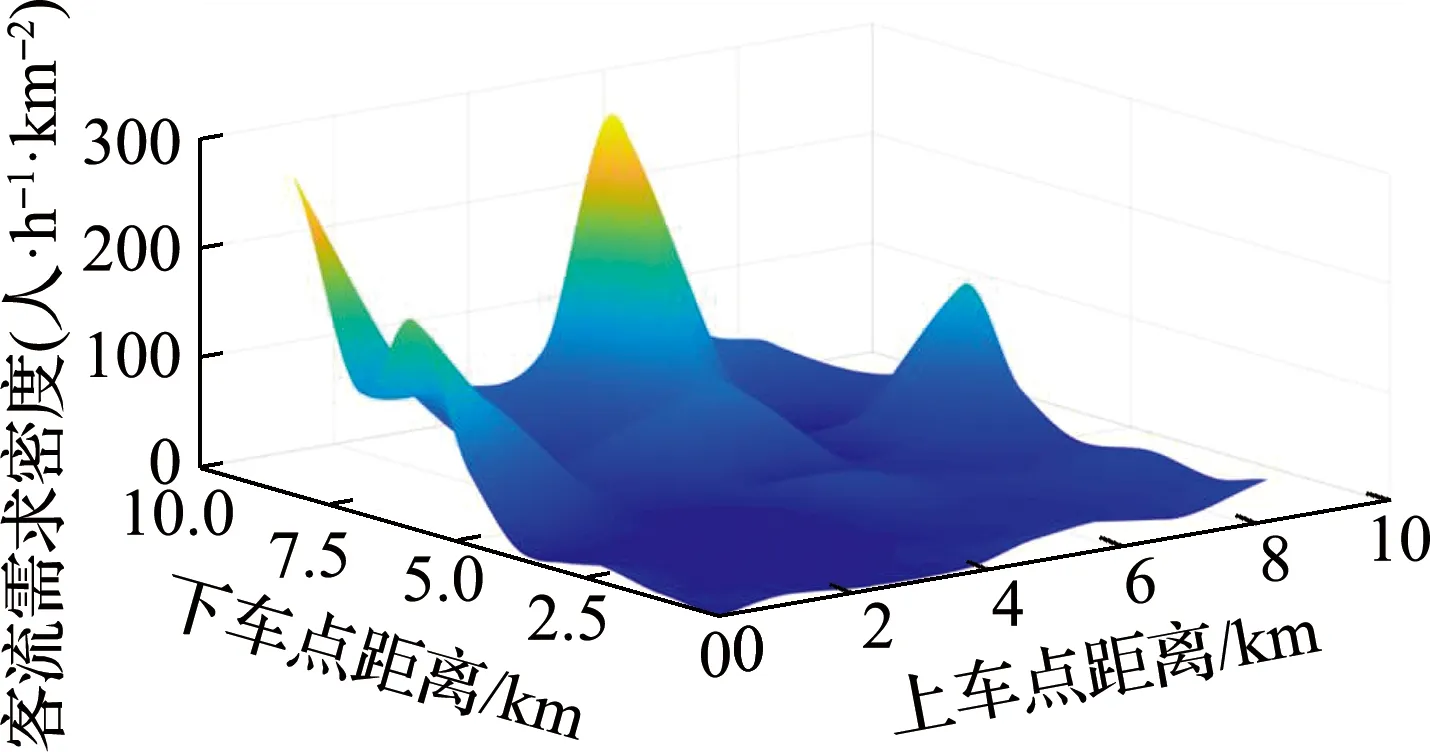
图3 离散公交客流拟合结果
3.1 参数取值
模型参数设置参考文献[22-29].轨道交通平均站点停靠时间为30 s,其余各参数取值为:vw=2 km/h,vb=25 km/h,vr=60 km/h,τ0=30 s,τa=2 s,τb=2 s,hmin=1.5 min,ξ=30 s,Kb=80 人/辆,μ=35 元/h,πt=123 元/(站·h),πl=4.13 元/(辆·km),πs=6.37 元/(站·h),ε=0.01.
3.2 试验结果
图4为现有公交线路与优化后公交线路的站点布局及其拟合密度,其中站点位置由中点法获得.由图可知,优化后的公交站点比当前公交站点数量更多.
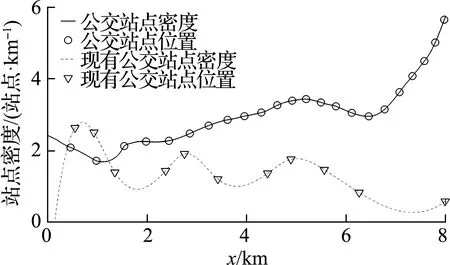
图4 优化前后公交站点及其拟合密度曲线
表1对比了优化前后的运营总成本、乘客出行总成本以及系统总成本.为统一单位,表中的成本项均采用由时间价值系数μ转化成的时间成本.由表可知,优化后虽然运营总成本增加了11.82%,但乘客出行总成本降低了32.54%,故系统总成本降低了27.14%.由此说明,优化后的公交系统运营效率更高.

表1 优化前后的公交服务各指标对比
为证明所提方法的有效性,对比了未考虑和考虑轨道交通条件下公交系统的优化结果(见表2).由表可知,在未考虑轨道交通的情况下,优化后的公交线路运营总成本和乘客出行总成本均更高.由此说明,对于由轨道交通和公交所构成的系统,需要从系统层面进行优化,而不能单独优化其中的某一种服务.

表2 考虑和未考虑轨道交通的优化结果对比
3.3 灵敏度分析
3.3.1 客流倍数
图5给出了不同客流条件下的优化结果.从图中可以看出,随着客流倍数的增加,逐渐形成较大的出行规模,促使平均公交站点距离和发车间隔减小,从而使乘客步行时间以及乘客等待时间减少,人均成本节省率增加.

(a) 人均成本节省率
3.3.2 站点建设和维护成本
图6给出了不同站点建设成本条件下的优化结果.由图可知,随着公交站点建设和维护成本的增加,所提方法的人均成本节省率逐渐降低.究其原因在于,公交站点建设和维护成本增加会导致公交站点数量减少,公交站间距离增大,从而使乘客步行距离增加,还会使公交接驳功能被削弱,越来越多的乘客直接步行前往轨道交通站点,导致公交客流量减少,公交车辆的发车间隔时间增大,人均成本节省率降低.

(a) 人均成本节省率
3.3.3 速度参数
图7为公交车辆不同速度时的优化结果.从图中可以看出,随着速度的增加,人均成本节省率以及平均公交站间距离呈先上升后下降然后缓慢上升的趋势.究其原因在于,速度较小时,公交的接驳优势不明显,乘客采用公交接驳轨道的比例较低;随着速度的增加,接驳优势逐渐明显,人均成本节省率也随之增加;但随着速度的进一步增加,公交车辆的速度与轨道交通的速度差距越来越小,公交的接驳功能逐渐弱化,2种交通工具之间形成客流竞争关系,使得系统的人均成本节省率逐渐下降;公交速度越来越快,即使2种交通工具形成竞争关系乘客也能从速度较快的公交中受益,因此系统的人均成本节省率逐渐增大.结果表明,在由2种不同交通工具形成的系统中,某种交通工具的功能与其速度密切相关,需要进行合理优化,以提高系统的运营效率.

(a) 人均成本节省率
4 结论
1) 相比于传统的离散建模方法,采用连续近似的方法对与轨道交通共线的公交线路进行优化具有能够获得解析解的优点,从而有效解决模型求解困难的问题.
2) 本文构建的轨道交通共线公交线路优化模型考虑了乘客到达站点的时间,克服了离散模型难以考虑乘客站点到离时间的缺点.
3) 不同于单一公交系统的优化方法,本文考虑了当前我国轨道交通和公交共线的实际情况,将两者作为一个系统进行建模,刻画了乘客在该系统中的出行选择行为,实现了系统最优方案的设计.

