安装方向对角接触球轴承保持架动态特性的影响
袁杜娟 ,陈晓阳* ,李清清 ,邱良伟 ,张 涛
(1.上海大学 机电工程与自动化学院,上海 200444;2.上海天安轴承有限公司,上海 201108)
角接触球轴承作为高速旋转动力装备的核心支承部件,其工作性能直接影响机械设备的寿命及精度.目前国内外对角接触球轴承的研究日渐完善[1-3],但仍是研究热点.由于高速工况下保持架的不稳定性会导致轴承的过早失效甚至设备无法正常运行,为了进一步提高轴承的工作性能,对保持架进行动力学建模与动态性能分析必不可少,进而为轴承的设计与应用提供理论指导.
目前理论研究主要集中在保持架的动力学模型、动态性能和失效形式等方面.Walters[4]首次分析了高速球轴承的动力学问题,计算出任意瞬时滚动体和保持架的位置和转速,仿真分析了球轴承中球与保持架的动态性能.随后几年,Gupta等[5]建立了所有零件具有六自由度滚动轴承的完全动力学模型,并开发了动力学分析程序ADORE.Wensing[6]运用ANSYS对球轴承进行模态分析和瞬态分析.Weinzapfel等[7]和Ashtekar等[8]采用离散元法建立了深沟球和角接触球轴承保持架的柔性模型,分析发现,柔性保持架可明显减小球与保持架兜孔的作用力,并可减少轴承达到稳态运转的时间.崔立等[9]运用ANSYS/LS-DYNA建立保持架的有限元模型,从保持架应力分布和动态响应中分析得出影响保持架稳定性和导致其故障的主要原因.姚廷强等[10]在ANSYS/LS-DYNA中建立了角接触球轴承的柔性多体接触动力学模型,进行接触仿真来分析球轴承的运动状态对保持架稳定性的影响.邓四二等[11]考虑保持架柔性变形影响获得保持架的质心轨迹.冯毅杰等[12]基于ABAQUS建立角接触球轴承有限元模型,通过施加不同的转速和载荷进行动力学仿真,从保持架质心运动轨迹和质心涡动速度偏差比两方面对其动态特性进行分析.涂文兵等[13]建立了轴承塑性材料柔性接触的非线性动态有限元模型,采用显式动力学LS-DYNA对其在三种不同转速波动形式下的非线性运行过程进行动态仿真,获得了转速波动工况下的保持架角速度曲线和打滑率曲线.呙如兵等[14]基于圆锥滚子轴承零件受力模型及润滑理论建立适用于冲击工况的轴承保持架动力学模型,考虑联合载荷和冲击载荷的作用,基于ANSYS/LS-DYNA分析了兜孔间隙和引导间隙对保持架动态特性的影响.相较于ADORE等仿真程序,不能考虑零件的柔性且无法分析应力的限制,借助有限元方法可以将保持架柔性化,从而对保持架应力进行精确分析.
试验研究方面,Kingsbury[15]最早通过试验研究发现球与保持架的摩擦引起保持架的涡动,保持架的不稳定涡动导致啸叫.立石佳男等[16]根据试验研究保持架质心轨迹形状,将保持架的运动区分为两种:低速高载时大体上停留在轴承内固定处,高速轻载时沿着外圈引导面做圆形运动,但结果中没有考虑重力因素的影响.国内黄迪山[17]、Wen等[18]和Han等[19]分别研制了适用不同轴承尺寸和工况的保持架动态性能试验机,研究了载荷、转速及保持架偏心质量对质心运动的影响.以上关于保持架动态特性试验的研究均需要对被试轴承做特殊加工处理,降低了试验结果的准确性.
以上文献中的研究成果对轴承的安装、适用工况和保持架的结构优化设计等提供了一定的参考.然而,目前的研究主要集中在使用工况、几何结构和材料等方面,很少考虑轴承安装方向对保持架动力学性能的影响.在有限元仿真方面,现阶段通用的有限元软件中轴承的三维模型建立、网格划分以及边界条件、载荷、接触对和分析参数设置等前处理占用了分析的绝大部分时间,且所得的结果缺乏验证,因此需要更全面的研究来分析保持架的动态特性.
本文中基于保持架动力学研究现状,运用课题组已有的深沟球轴承静力学有限元前处理系统[20],实现角接触球轴承有限元模型的参数化建模,将保持架柔性化,并结合试验验证仿真结果的可靠性,进而研究轴承的水平以及竖直安装方式对保持架动态特性的影响,其结果可为滚动轴承的理论研究以及实际应用中的轴承安装提供参考.
1 有限元模型的建立与求解
1.1 角接触球轴承有限元仿真前处理
针对滚动轴承的运动特点,在建立完整的轴承仿真分析模型中做出如下的假设条件:
(1) 不考虑倒角、圆角及对接触分析没有影响的其他微小几何结构;
(2) 角接触球轴承的仿真模拟过程中忽略游隙和油膜的影响;
(3) 考虑轴承的塑性变形较小,不考虑材料非线性特性,假设轴承的元件(内圈、外圈和滚动体)采用线弹性材料,保持架可采用线弹性或者刚性材料.
运用有限元软件MSC Patran的命令语言PCL,对仿真前处理程序进行二次开发,利用模块化设计思想,将整个角接触球轴承动力学有限元前处理系统划分为4个模块,如图1所示.选择相应的模块进入对话框,只需要输入轴承的几何参数、材料参数和载荷参数,程序就会自动控制生成角接触球轴承的内外圈、球和保持架的三维实体模型以及有限元网格模型,并由程序驱动自动完成材料属性的设置以及转速和载荷等边界条件的施加.
在轴承的动力学特性有限元分析中,关键是网格划分以及接触设置.为了兼顾计算精度和速度,采用了六面体网格划分及等距或者以长度等比递增方式进行布网格划分种子[21],接触区域网格划分细致,非接触区域划分较粗.接触设置为自动面-面接触,通过设置判断循环语句来完成接触设置.设置有3n+1 (n为滚动体个数)对接触对,分别为滚动体与内圈、外圈和保持架兜孔的接触以及保持架与引导套圈的接触.表1列出了摩擦系数值,fs为静摩擦系数,fd为动摩擦系数.摩擦系数的设置虽会影响质心轨迹的形状以及等效应力的大小,但不会改变安装方式对保持架质心轨迹影响的规律趋势,同时也不会改变最大等效应力发生的位置.本文中仿真过程忽略游隙和油膜的影响,考虑到保持架与球及套圈挡边之间的相对滑动速度较大,因此动摩擦系数均设为恒定值0.05[2],本文中所做分析以此为参考,也可根据具体工况作相应的设置.
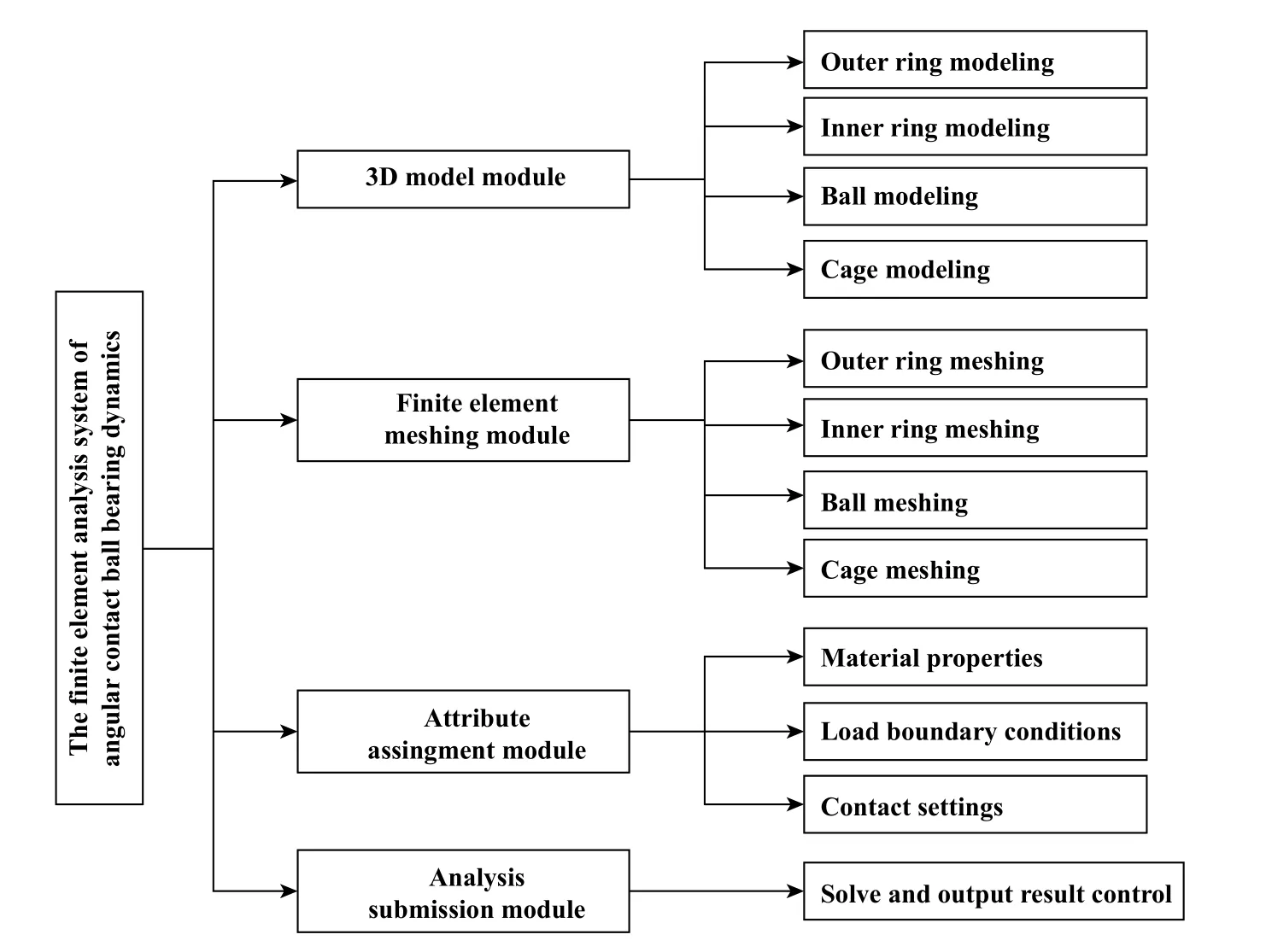
Fig.1 Pre-processing system for simulation analysis图1 仿真分析前处理系统

表1 摩擦系数设置Table 1 Setting of friction coefficient
为便于后续分析,将轴承的安装方向分为水平安装和竖直安装,建模后可获得图2所示的两种安装方向的角接触球轴承的有限元模型,其中g代表重力方向.
1.2 前处理结果文件计算及后处理分析
经过集成自动化的前处理操作后生成求解需要的key文件,前处理模型的信息包括节点信息、单元信息、接触设置和载荷等.在求解提交key文件前对此文件进行关键字修改,例如仿真的时间、步数、轴承的工况(轴承的转速、载荷及摩擦系数等)及重力加速度方向等的设置.
有限元动力学分析一般采用显式算法,本文中采用Ls-Dyna求解器进行求解,主要运用中心差分法,避开了对线性方程组的迭代求解,很大程度上节约了计算的求解时间.在显式动力学有限元分析中,系统的求解方程式为
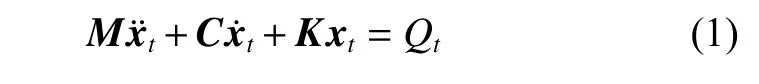
在中心差分法中,加速度和速度可以用位移表示为

其中:Δt为时间步长,由此可得个离散时间点的位移递推公式为

由于模型网格数量较多且为动力学,计算量大,因此借助上海大学集群式高性能计算机“自强4 000”进行求解.计算完成后运用后处理分析软件Ls-prepost提取结果,可以清晰直观地得到整个仿真时间内轴承各零件的动态过程.
2 模型的验证
2.1 试验验证
作者所在课题组使用的配对轴承差动保持架动态特性试验装置在不需要改变试验轴承结构的基础上,能精确测量保持架在不同旋转工况下的运动情况[22].试验装置实物和结构图如图3和图4所示.在被试轴承外圈固定的工况下,电主轴驱动内圈旋转,由高速摄像机清晰地记录保持架的运动情况,通过图像处理得到轴承保持架在径向平面内的位移量,从而绘制出保持架的质心轨迹.
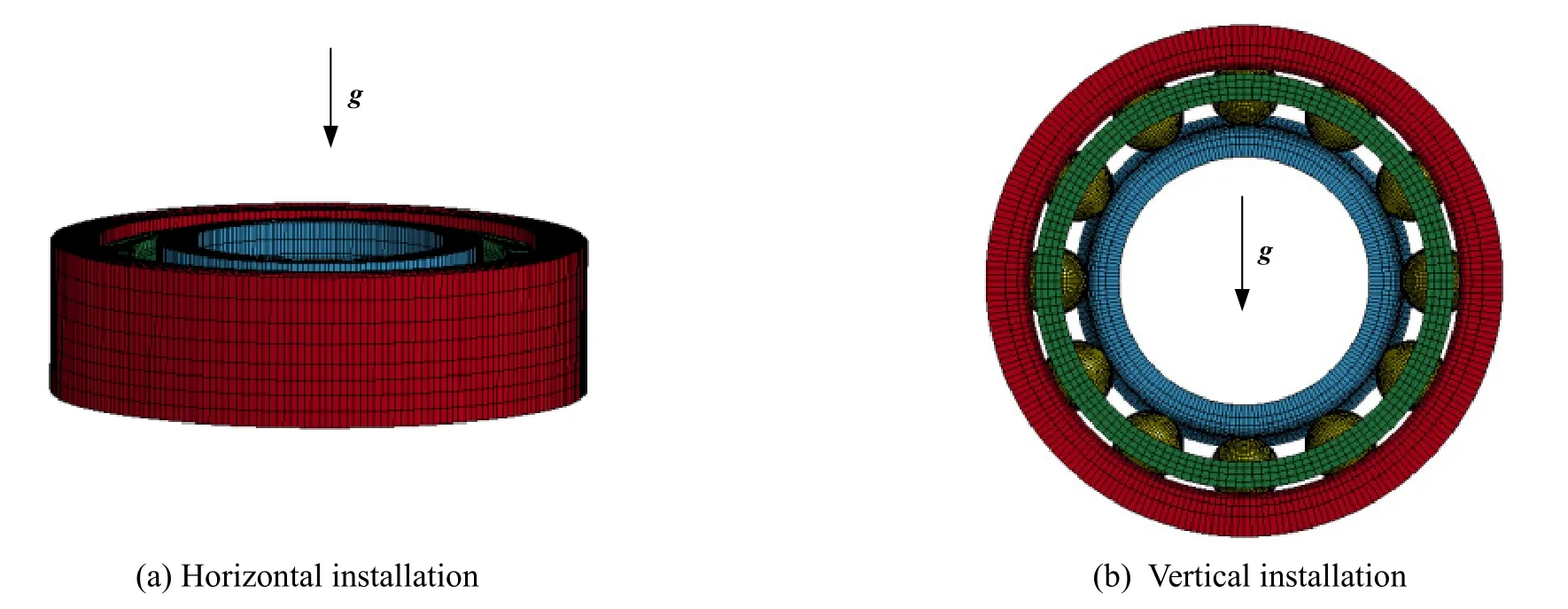
Fig.2 Finite element models of angular contact ball bearings in different installation directions图2 不同安装方向时角接触球轴承的有限元模型

Fig.3 Photograph of test device图3 试验装置实物图
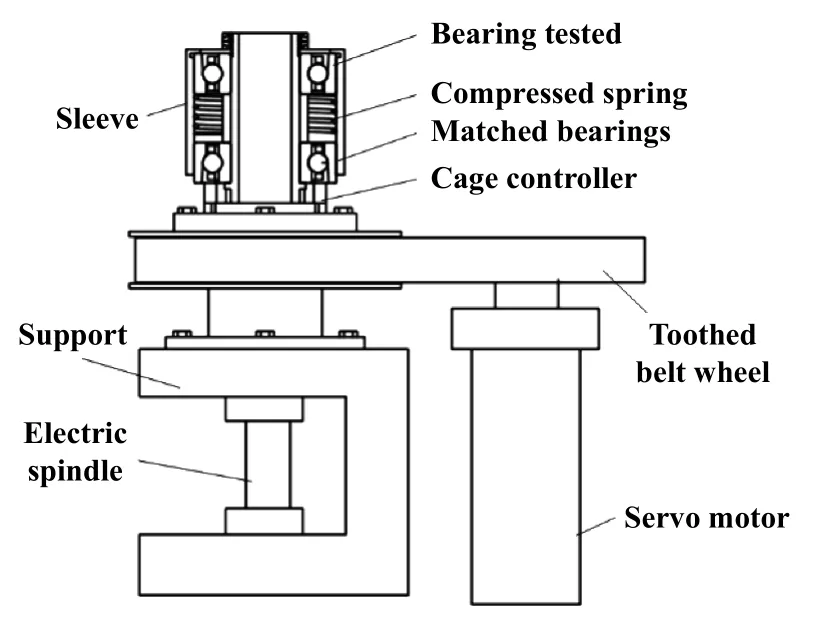
Fig.4 Structure diagram of test device图4 试验装置结构图
为了精准定量分析保持架质心轨迹运动图像,需要对拍摄照片进行图像处理,首先采用边缘检测(Canny算子[23])对图像进行边界提取,再进行Hough变换[24]取圆,对提取出的相应圆的点采用最小二乘法对其进行拟合,最后根据拟合的边界圆得到保持架的质心位置.保持架质心提取的图像处理过程如图5所示,保持架上白点标记可用于在控制转速时辨别保持架是否发生公转.
采用7003C角接触球轴承作为试验与仿真分析对象,其几何参数和材料参数列于表2和表3中.ni表示轴承的内圈转速,设置轴承的工作条件为内圈转速3 000 r/min,轻预紧工况下轴向载荷25 N.将本文中有限元仿真结果与试验得到的质心轨迹进行对比,保证试验工况的一致性,得到稳定状态时的保持架质心轨迹如图6所示,Y和Z分别表示保持架在径向平面内的位移.

表2 7003C角接触球轴承结构参数Table 2 Structural parameters of angular contact ball bearing 7003C

表3 7003C角接触球轴承材料参数Table 3 Material parameters of angular contact ball bearing 7003C
从图6所示的保持架的质心轨迹可以看出,本文中有限元仿真结果与试验中所得到的保持架的质心轨迹形状接近,质心轨迹半径较为一致,从而证明了利用本文中的有限元方法进行轴承动态性能仿真结果的可靠性.
2.2 文献验证
有限元仿真分析7220C角接触球轴承水平安装时保持架的质心运动轨迹,为进一步保证仿真分析结果的可靠性,与文献[25]的结果以及轴承动力学商业分析软件ADORE的结果进行对比.轴承的工作条件如下:外圈固定内圈旋转,内圈转速1 000 r/min,纯轴向载荷为100 N.由于程序运算较为费时,本文中仅仿真轴承运行0.7 s,而文献中试验时间为16.75 s,为便于对比,提取文献中2.28~3.04 s的试验数据,得到图7(b)的结果,可以看出,文献结果、ADORE数值仿真结果以及本文中有限元结果呈现的保持架的质心轨迹基本吻合,其质心轨迹近似呈圆形,且相较于ADORE的结果,利用本文中有限元方法得到的质心轨迹与文献结果更为接近,充分验证了本文中有限元仿真计算结果的正确性.
3 结果与讨论
同样以7003C角接触球轴承为研究对象,仿真分析了水平安装方向以及竖直安装方向对保持架动态特性的影响.轻预紧工况下轴承承受纯轴向预载荷为25 N,保持架有限元模型共有9 216个单元,13 620个节点,轴承有限元模型有217 420个单元,238 296个节点,仿真时间为0.3 s.
3.1 安装方向对保持架质心轨迹的影响
轴承外圈固定,内圈转速分别为3 000、6 000和9 000 r/min,当轴承水平和竖直安装时,保持架的质心轨迹分别如图8(a)和图8(b)所示.

Fig.5 Image processing for extraction of cage centroid图5 保持架质心提取的图像处理过程
从图8可以看出,转速低于6 000 r/min,当轴承水平安装时,保持架的质心轨迹近似圆形;当轴承竖直安装时,保持架质心轨迹在偏离轴承中心的下方某点附近晃动.转速大于6 000 r/min,轴承水平和竖直安装时,保持架稳定之后均可以形成近似圆形的质心轨迹.
在低速工况下,轴承竖直安装时,保持架的重力方向与保持架离心力均在轴承径向平面内,保持架的离心力不足以克服重力作用,易在轴承下方某点形成无规则运动;轴承水平安装时,保持架的重力方向与轴承轴向重合,保持架的重力均匀分配在滚动体上,滚动体的公转速度恒定,保持架与滚动体及套圈的接触碰撞和摩擦作用易使保持架形成圆形的涡动轨迹.

Fig.6 Cage centroid orbit for ni=3 000 r/min图6 ni=3 000 r/min时保持架质心轨迹
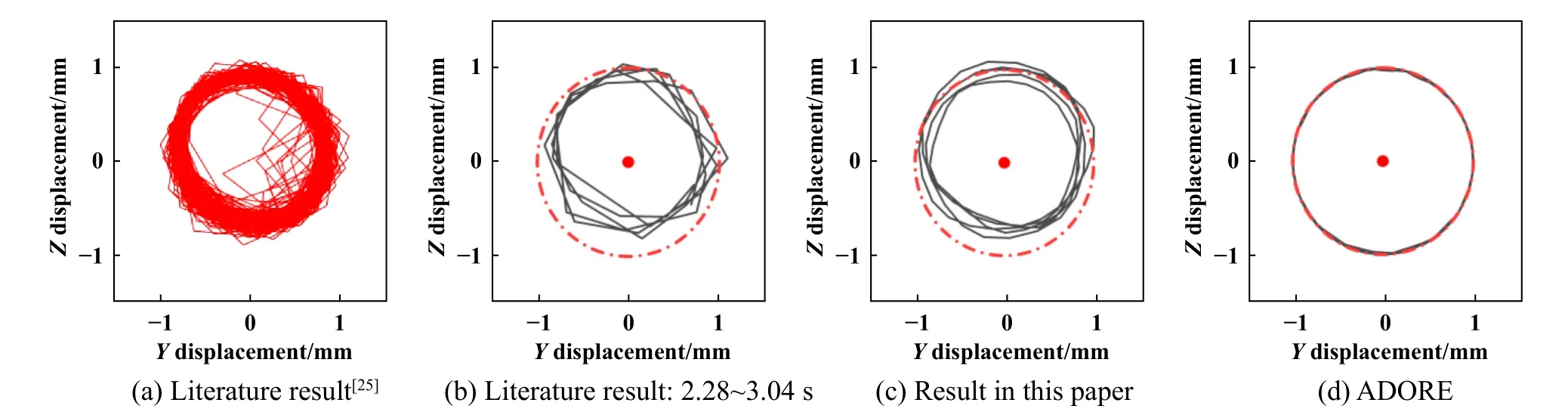
Fig.7 Comparison of cage centroid orbit in three methods图7 三种方法的保持架质心轨迹比较

Fig.8 Comparison on the cage centroid trajectory under different rotation speeds and installation directions图8 不同转速及安装方向工况下保持架质心轨迹比较
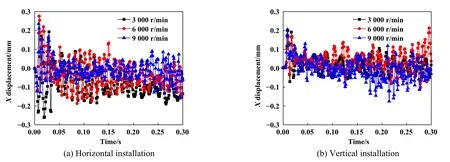
Fig.9 Axial displacement of the cage versus time图9 保持架轴向位移随时间变化曲线
图9所示为不同转速两种安装方式时保持架的轴向位移,对其求标准差后得到的结果列于表4中.内圈转速分别为3 000、6 000和9 000 r/min,水平安装时轴向位移的标准差分别为0.075、0.076和0.088,竖直安装时轴向位移标准差分别为0.045、0.051和0.07.可以看出,轴承水平安装相较于竖直安装,轴向位移的波动幅度较大,此时保持架的重力方向沿轴向,球与保持架的碰撞作用使保持架在轴向的合力增加,轴向的振动增加.随着转速增加,两种安装方向下的轴向位移波动幅度均增加,但两种安装方式的波动性差值有所减小,说明低速时安装方式对保持架的运动影响更大.

表4 保持架轴向位移的波动性比较Table 4 Comparison of volatility of axial displacement of cage
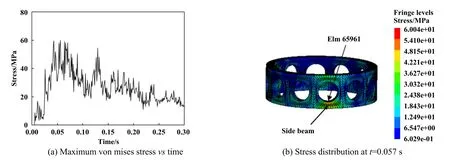
Fig.10 Maximum von mises stress vs time and stress distribution of the cage for bearing with horizontal installation when ni=3 000 r/min图10 ni=3 000 r/min时轴承水平安装时保持架最大等效应力-时间曲线及应力云图
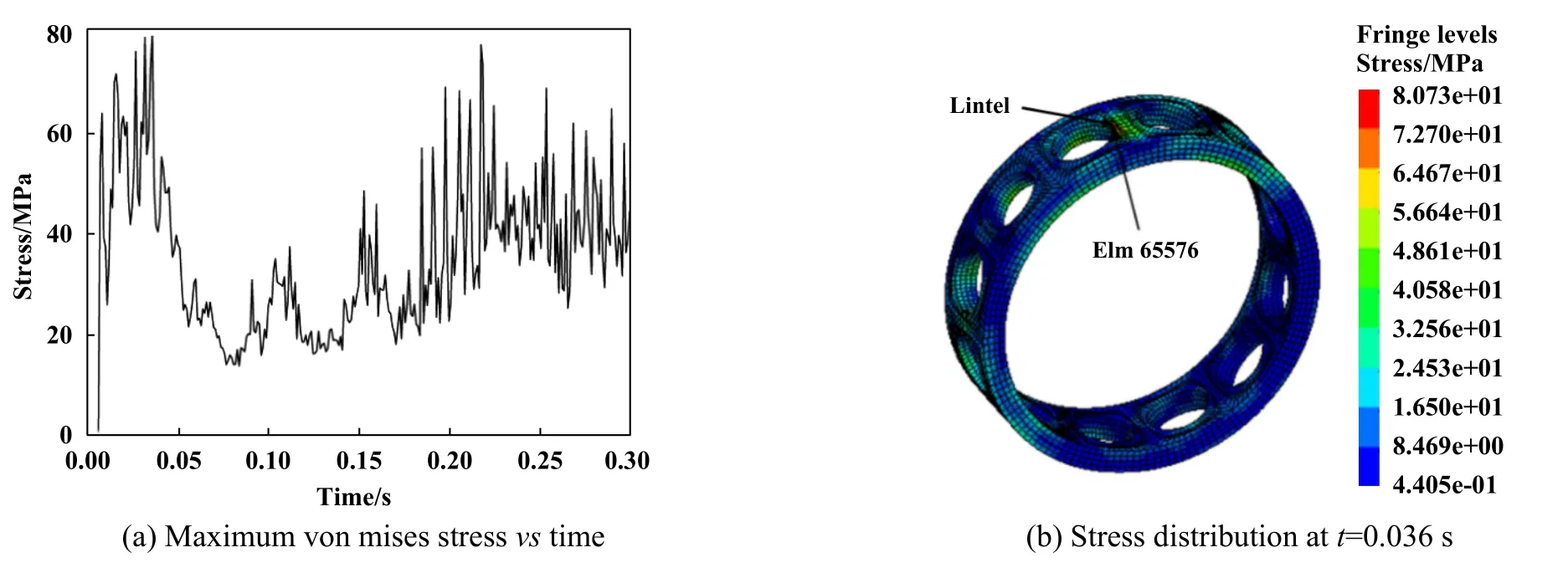
Fig.11 Maximum von mises stress vs time and stress distribution of the cage for bearing with vertical installation when ni=3 000 r/min图11 ni=3 000 r/min时轴承竖直安装时保持架最大等效应力-时间曲线及应力云图
3.2 最大等效应力分析
对保持架上最大等效应力随时间变化仿真分析,得出图10和图11所示的结果,内圈转速为3 000 r/min,轴承水平安装时,最大等效应力平均值为26.03 MPa,0.057 s时在保持架兜孔的侧梁位置(对应单元为65961)出现最大应力值60.04 MPa;竖直安装时最大等效应力平均值为34.62 MPa,0.036 s时保持架兜孔过梁位置(对应单元为65576)出现最大值80.73 MPa.
从表5可以看出,随着转速的增大,保持架上的应力增大,同一转速下竖直安装时保持架上的最大应力值较大.低速工况下,竖直安装时,保持架最大应力发生在过梁位置,水平安装时最大应力发生在侧梁位置;高速工况下,两种安装方向的最大应力均发生在过梁.在重力作用下,竖直安装时,滚动体分布不均,公转速度不恒定,与保持架兜孔的瞬时碰撞作用增大,且在过梁位置发生碰撞时的法向速度分量较大,从而产生较大应力;而水平安装时,滚动体与保持架兜孔在侧梁位置发生碰撞时的法向速度较小,因此接触应力小于竖直安装的应力值.

表5 不同转速下保持架上最大等效应力比较Table 5 Comparison of the maximum equivalent stress on the cage at different speeds
4 结论
本文中利用有限元软件MSC Patran的二次开发模块实现了角接触球轴承的参数化建模与动力学仿真,通过与试验结果对比,验证了本文中所建立的有限元参数化模型的有效性.基于该模型,分析了角接触球轴承水平与竖直安装方向对保持架稳定性以及应力的影响,得到如下结论:
a.轴承竖直安装时,在较低转速下由于重力作用,保持架质心在偏离轴承中心一侧无规则摆动,转速较高时保持架易形成近似圆形的质心轨迹.轴承水平安装时重力方向与球对保持架作用力的轴向分量方向一致,在离心力作用下,不同转速下的保持架质心运动轨迹近似圆形.
b.轴承在不同转速下运转,随着滚动体与保持架碰撞点位置的变化,进而影响保持架上的最大应力值及最大应力位置的变化.同一工况下竖直安装时保持架上的最大应力值较大;低速工况下,竖直安装时保持架最大应力发生在过梁位置,水平安装时最大应力发生在侧梁位置;高速工况下,两种安装方向的最大应力均发生在过梁位置.

