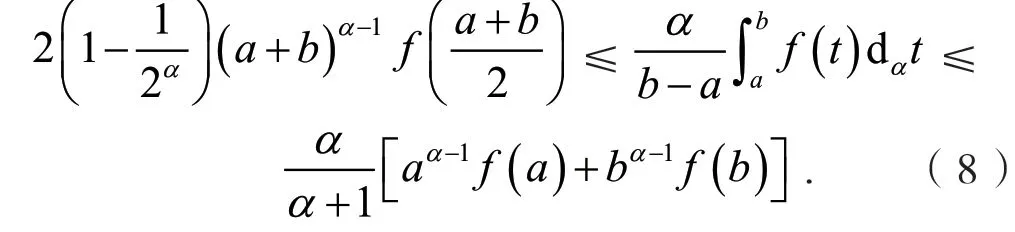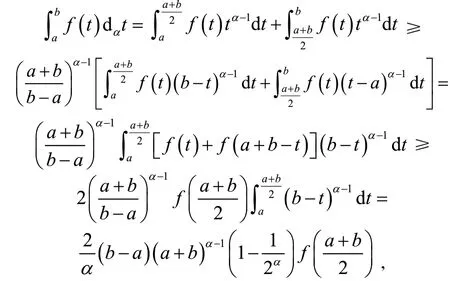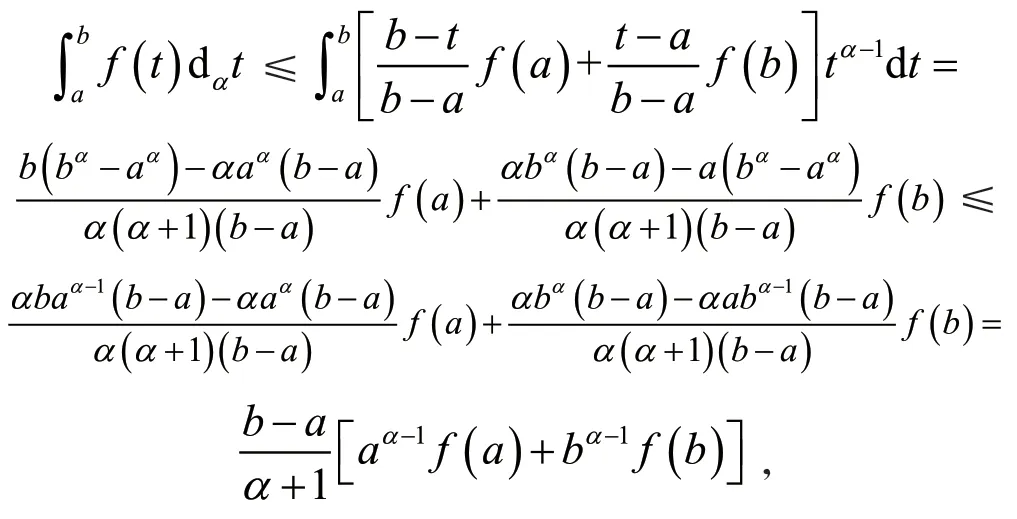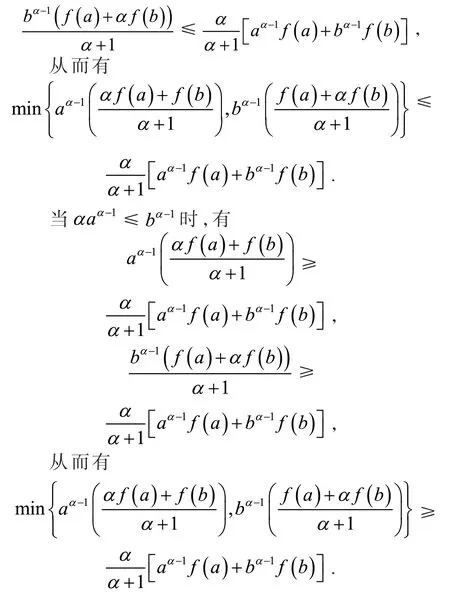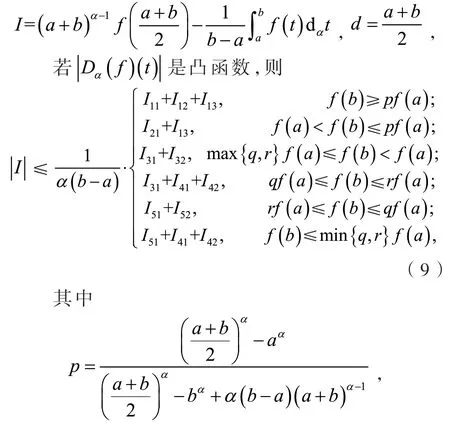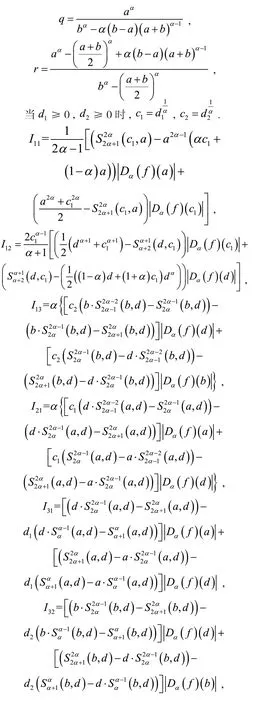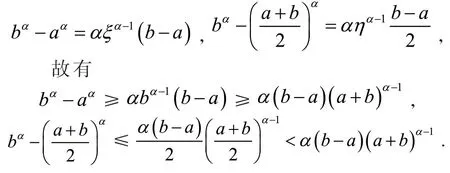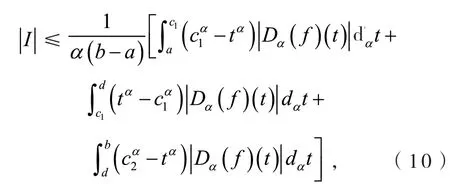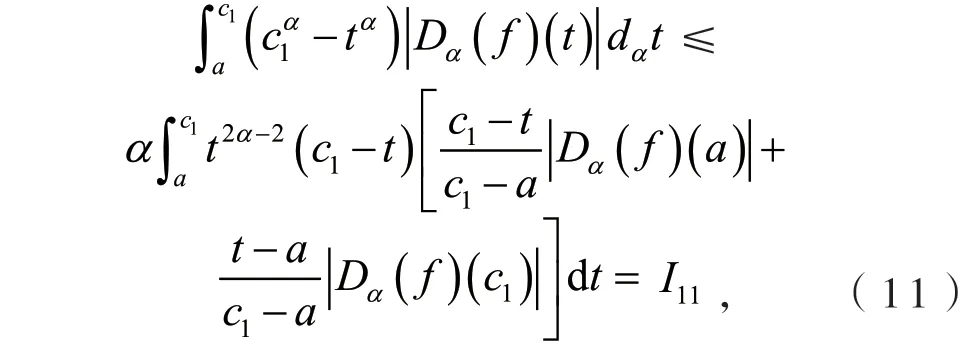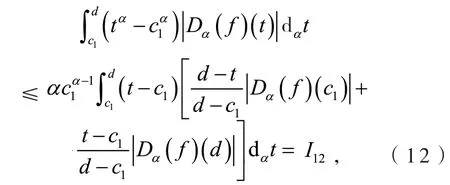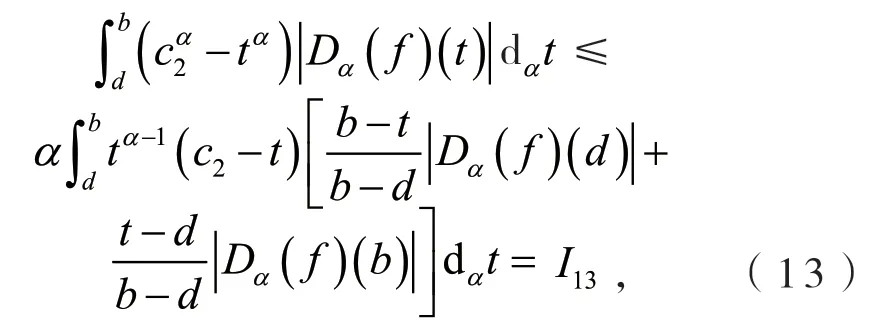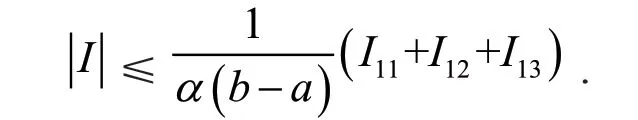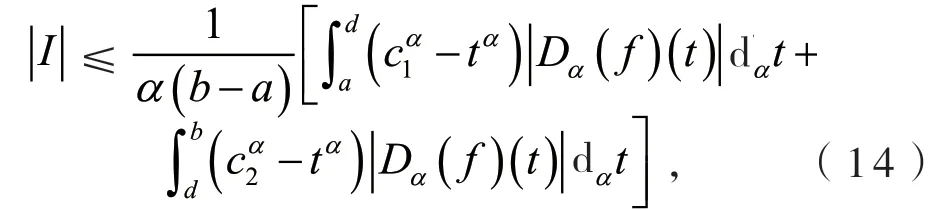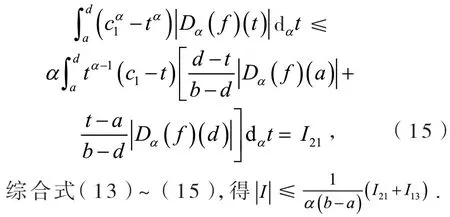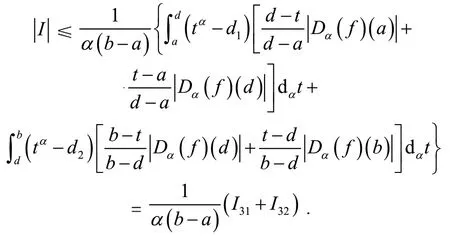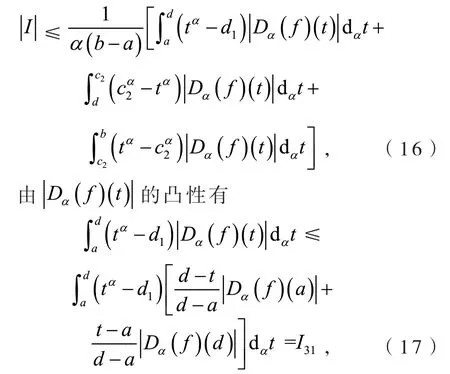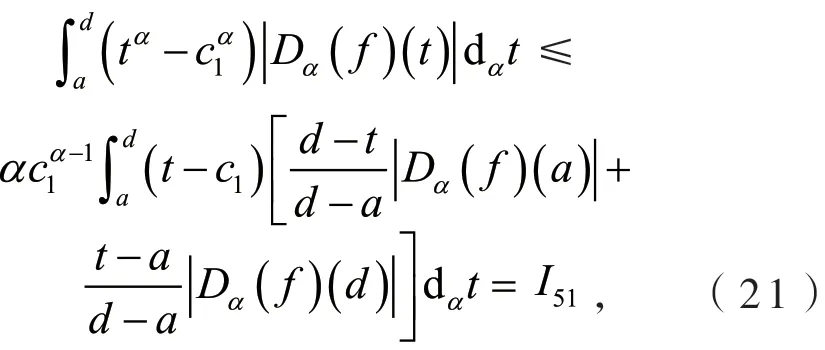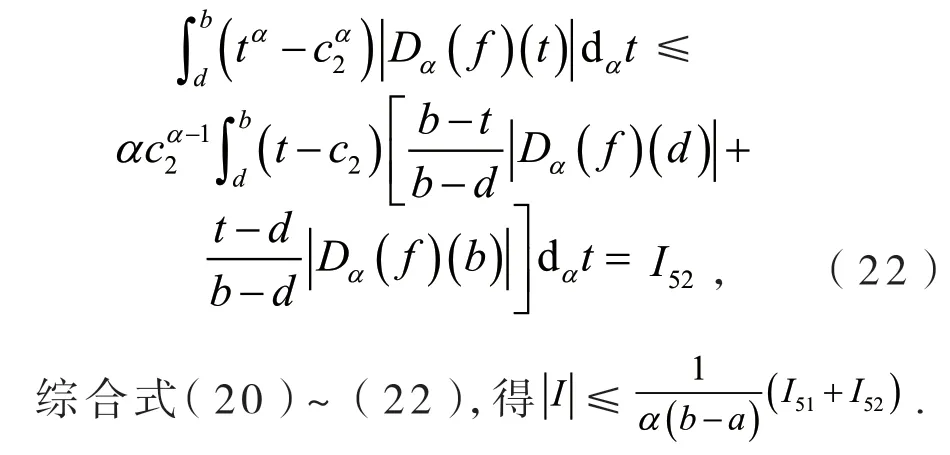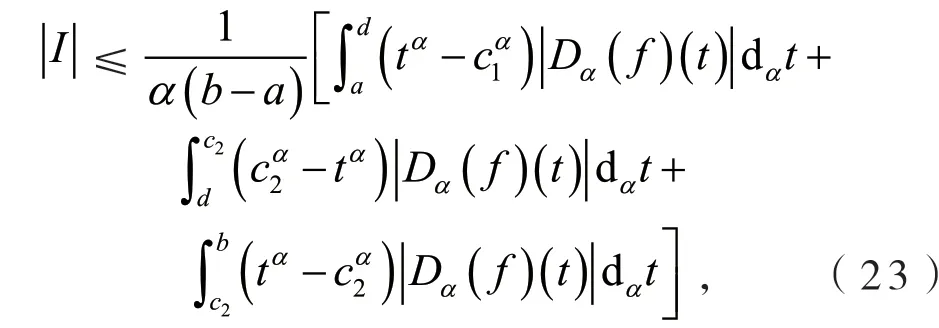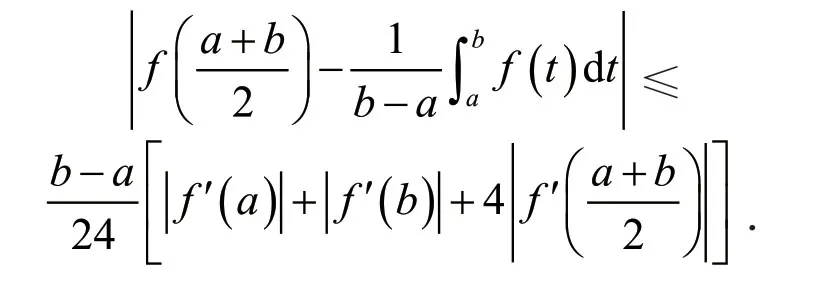一致分数阶积分的Hermite-Hadamard型不等式及差值估计
曾志红,时统业,曹俊飞
(1.广东第二师范学院 学报编辑部,广东 广州 510303;2.海军指挥学院,江苏 南京 211800;3. 广东第二师范学院 数学学院,广东 广州 510303)
1 引言和引理
设f是[a,b]上的凸函数(即对于任意x,y∈[a,b]和任意λ∈[0,1]有f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)),则有著名的Hermite-Hadamard不等式成立:
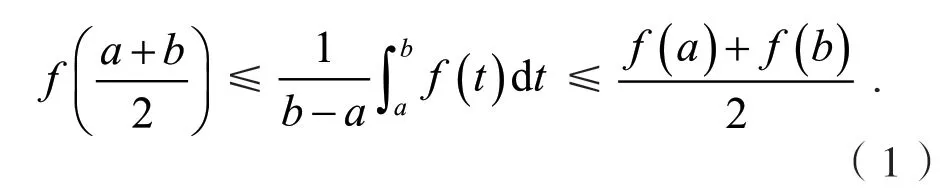
关于Hermite-Hadamard不等式的改进、推广和加细可见文献[1-3].
利用一阶导数可估计由式(1)生成的差值[4-5].
文[6]引入一致分数阶导数和一致分数阶积分的定义.
定 义1[6]设0<α≤1,f:[0,∞)→R在点t>0处的一致α分数阶导数定义为
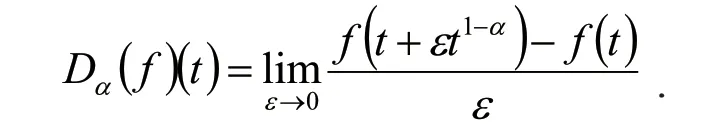
如果f在某个区间(0,a)是一致α分数阶可导的,且存在,则定义
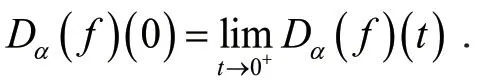
当f在点t处可微时,Dα(f)(t)=f′(t)t1−α.如果f在区间I上每一点处的一致α分数阶导数都存在,则称f在区间I上是一致α分数阶可微的.
定义2[6]设0<α≤1,0≤a 存在,则称f在[a,b]上是一致α分数阶可积的. 引理1[7](一致分数阶积分分部积分法)设0<α≤1,0≤a 定理1[8](一致分数阶Hermite-Hadamard型不等式)设α∈(0,1],f:[a,b]→R一致分数阶可微, (1)若Dα(f)(t)单调增加,则有 (2)若Dα(f)(t)单调增加,f单调减少,则有 定理2[11]设α∈(0,1],0 引理2[11]设α∈(0,1],0 文[11]给出了由式(4)的左边生成的差值的估计,本文将给出这个差值的新的估计. 引理3 设α∈(0,1],0≤a 证明 由引理1有 将式(6)与式(7)相加,则式(5)得证. 定理3 设α∈(0,1],0 证明 利用引理2,有 式(8)的左边不等式得证. 由f的凸性及αbα−1(b−a)≤bα−aα≤αaα−1(b−a),有 式(8)的右边不等式得证. 注1 式(8)的左边不等式是式(4)的左边不等式的加强.事实上,由贝努利不等式,对任意有xα≤1+α(x−1)≤1−αx,故有 注2 式(8)的右边不等式与式(4)的右边不等式各有强弱.事实上,当αaα−1≥bα−1时,有 定理4 设α∈(0,1],0 利用微分中值定理,存在ξ∈(a,b),,使得 (i)当f(b)≥pf(a)时,有a≤c1≤d,c2≥b,由引理3有 对任意t∈[a,c1],有,由的凸性有 对任意t∈[c1,d],有,由的凸性有 对任意t∈[d,b],有,由的凸性有 综合式(10)~(13)得 (ii)当f(a) 对任意t∈[a,d],有,又由的凸性有 (iii)当max{q,r}f(a)≤f(b) (iv)当qf(a)≤f(b)≤rf(a)时,有d1≤0,d≤c2≤b,由引理3有 对任意t∈[d,c2],有,又由的凸性有 对任意t∈[c2,b],有,又由的凸性有 (v)当rf(a)≤f(b)≤qf(a)时,有0≤c1≤a,0≤c2≤d,由引理3有 对任意t∈[a,d],有,又由的凸性有 对任意t∈[d,b],有,又由的凸性有 (vi)当f(b)≤min{q,r}f(a)时,有0≤c1≤α,0,d≤c2≤b,由引理3有 式(9)得证. 推论1 设α∈(0,1],0≤a 证明 在定理4(i)和(iii)中 取α=1即 可得证.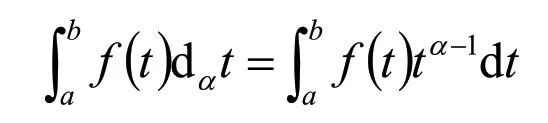
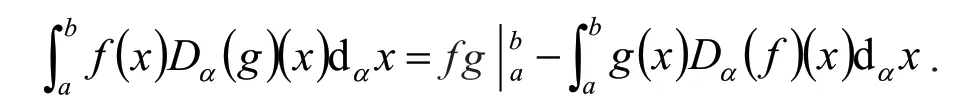
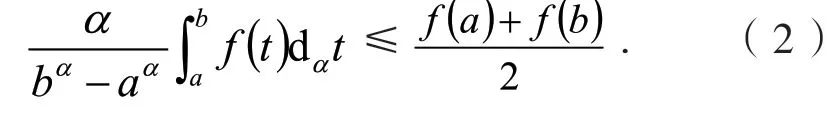
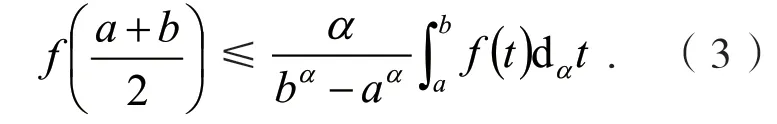
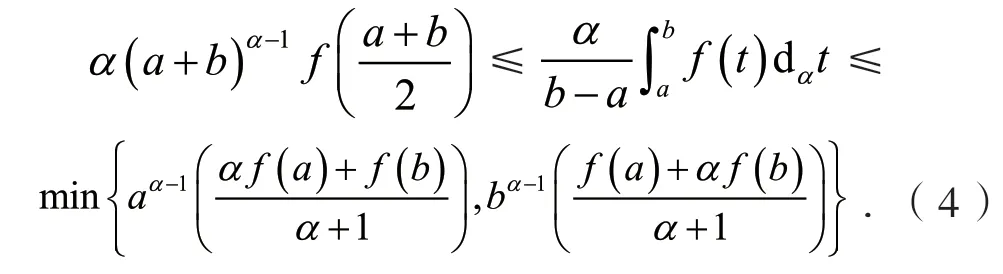
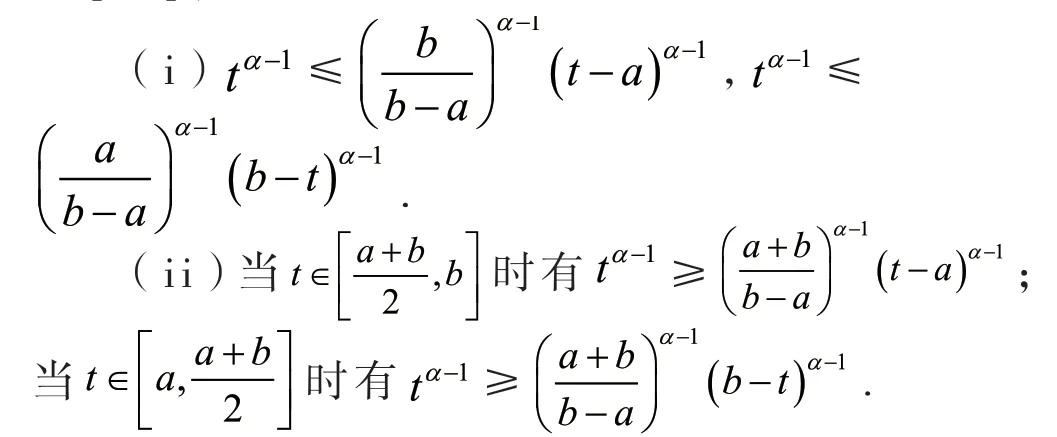

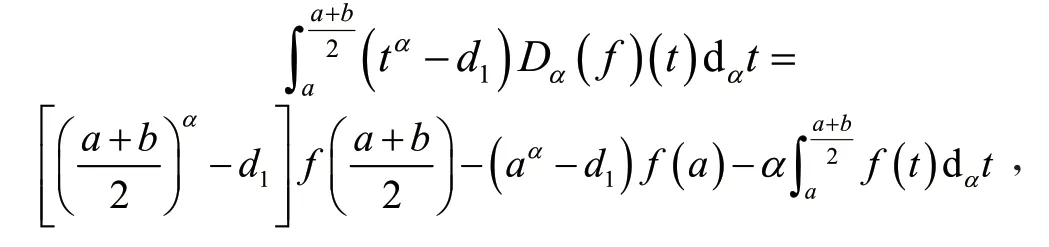
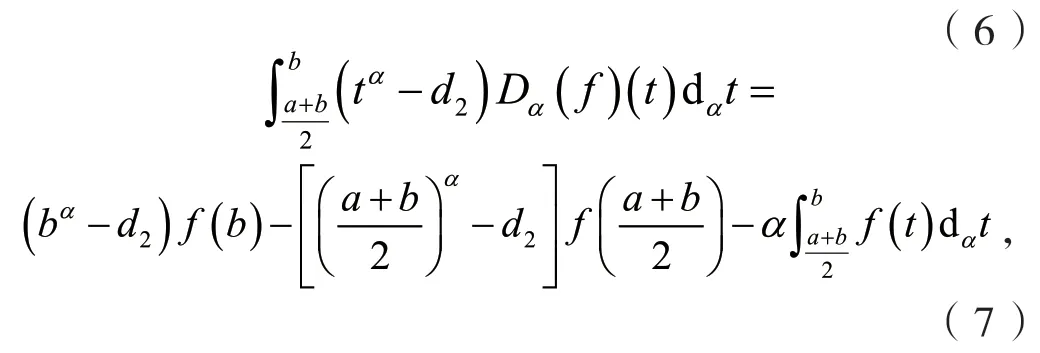
2 主要结果