一种基于聚类与噪声的网络流量分类方法*

庞兴龙，朱国胜，杨少龙，李修远

(湖北大学计算机与信息工程学院，湖北 武汉 430062)

1 引言

网络流量分类离不开数据集的标签，其中监督学习和半监督学习最具有代表性，并且具有较高的准确率。目前大多数研究人员利用现有的公开数据集或者自主采集的数据集，经过人工周密的标记达到分类的目的，但一般都建立在无噪声环境影响的前提下，而现实情况中的网络流量通常携带或多或少的外部噪声。研究人员将外部噪声分为2类：标签噪声和特征噪声。标签噪声是指在分类过程中被用于训练的目标标签与数据集本身对应的标签存在差异，例如，在标签标记时将某条数据归属于其他标签，标签名称拼写错误等情况都会导致出现标签噪声；特征噪声通常指训练集样本的特征与实际样本训练特征的差异，例如人为注入的高斯噪声。以上2种噪声均会对分类性能造成一定的影响，并且许多科研工作者论证得出标签噪声造成的影响会更加显著的结论。Frénay等人[1]对这一类型的噪声进行了充分的描述，Quinlan[2]对2种噪声的影响进行了分析并得出了类似的结论:相对于特征噪声,标签噪声对分类器的影响更大。因此,本文着重分析标签噪声问题对分类性能的影响。

标签噪声在分类问题中对分类性能具有较大的影响，通常直接表现为分类能力大幅度下降、模型的复杂度增加和预测能力下降等。目前对于标签噪声的处理方法大致归为2种：(1)标签修复;(2)标签剔除。二者的目的都是减少错误标签对分类性能的影响，但本质上的区别在于标签剔除仅仅只是删除了被认为错误标记的数据，对于错误标签极少且剔除性能较高的算法，会有较好的分类结果，但通过剔除达到除噪目的的方法在各种网络流量数据集上不一定有较好的适用性能,而标签修复在这种情况下具有更好的通用性。

2 相关研究

目前，对于标签的修复有2种处理方法：(1)对分类算法本身进行提升，如提升算法对噪声的鲁棒性、设计对标签噪声不敏感的算法等。文献[3]提出的自适应投票噪声校正算法，通过考虑潜在标签噪声的数量和概率创建多个弱分类器，来精确识别和校正潜在的噪声标签。Nettleton等人[4]通过对不同分类器在不同噪声比例下的稳定性进行对比，评判各个分类器对噪声的敏感度；Manwani等人[5]探讨了分类器的耐噪音学习，使用有、无噪声数据学习，使得分类器具有耐噪抗噪性能；Abelln等人[6]提出一种袋装信条决策树，来提高带噪数据集的分类性能，并且使用双变量误差分解分析验证了该算法具有较高的性能；Wang等人[7]则提出一种抗噪声统计流量分类方法，将噪声消除和可靠性估计技术引入流量分类中，在构建分类器之前，估计剩余训练数据的可靠性。通过在2个真实流量数据集上的大量分类实验得出，该方法能够有效地解决训练数据的错误标注问题。然而，这类算法对于数据集标签具有一定的依赖性，当标签噪声数目较多时，该算法所训练出的分类模型会受到显著影响。并且由于不同数据集自身特性的差异，该算法在各类数据集上的表现也存在差异。(2)在数据集层面上的修复，这类方法主要作为一种预处理手段来对数据集中带噪标签进行检测。文献[8]利用属性之间以及属性和类之间的相互依赖性，使用其余属性和类值预测该属性的值。通过识别每个实例中可能存在的噪声属性或类，并用更合适的值替换这些值来处理训练数据中的噪声，最终证明了这是一种可行的降噪和矫正方法。Arazo等人[9]提出了一种基于卷积神经网络的标签噪声下的训练方法，将生成的模型用于实现动态自举损失，并将这种动态自举与混合数据增强相结合，实现了一种非常稳健的损失校正方法。

可以发现，与基于算法层面的方法相比，基于数据层面的方法能从根本上改善数据集中的噪声含量，并且在噪声比例较高情况下能实现标签修复和分类，具有较高的挑战性和实用性。本文考虑从噪声根源出发，致力在数据与噪声标签之间挖掘新的联系，对噪声标签进行识别和修复。

3 基于标签噪声修复的网络流量分类方法

本文将K-means聚类算法和随机森林算法相结合, 提出了基于标签噪声修复的网络流量分类方法。K-means聚类算法作为典型的无监督算法，在没有可用标签的情况下，参与数据集预处理过程，为训练集训练出相应标签集。随机森林算法作为少数较优算法，对标签噪声不敏感[10]，能有效提高分类性能，因此本文实验将采用随机森林算法作为最终的分类模型。

本文方法考虑将权重值与聚类相结合，K-means聚类算法作为无监督学习技术，在分类中不会将标签作为分类的依据，因此在进行多次聚类后生成多组聚类的标签,然后调用CalcWeights算法[11]对聚类生成的多组标签计算权重，通过簇内具有优势值的标签来统计权重，原理是具有优势值的标签在簇内会表现出最优的标签类型。然而，CalcWeights算法依赖于训练集样本标签种类数目，因此只能处理正确标签被错误标记情况下的噪声，而无法识别由于错误拼写出现的新标签类型，这给权重值计算带来的影响较大。本文将标签错误拼写同时作为标签噪声产生的又一特殊情况，并改善了CalcWeights算法无法识别“新标签”的不足。首先对输入的训练集数据进行标签类型识别，设定标签数量阈值作为评判该标签类型是否为拼写错误的依据。图1展示了本文提出的带噪标签修复的网络流量分类方法的流程图：本文方法在对训练集进行标签类型和数量的统计后会将标签类型对应的数目与自定义阈值进行比较，并更新训练集中的标签和对应数量，再将K-means算法与CalcWeight算法循环执行a次，根据每次聚类生成的标签分布情况，为标签集赋予权重累加并输出最大权重值对应的标签类型，最后将标签集作为随机森林算法的输入。

Figure 1 Network traffic classification method based on label noise repair图1 基于标签噪声修复的网络流量分类方法

K-means聚类算法是目前应用最为广泛的聚类算法之一，具有算法简单、容易收敛的特性，目的是将未标注的数据集通过计算样本项之间的相似度(也称为样本间的距离)，按照数据内部存在的数据特征将其划分为不同的类别，使类内数据相似，类间数据差异大。

K-means聚类算法的基本流程如算法1所示。

算法1K-means聚类算法

输入：样本集D={x1,x2,…,xn}，聚类的簇数k。

输出：簇划分结果C={C1,C2,…,Ck}。

步骤1从样本集D中随机抽取k个样本作为聚类的质心向量，表示为{μ1,μ2,…,μk}。

步骤2以下步骤迭代n次：

(1)初始化各个簇类：Cm≠∅，m=1,2,…,k；

(4)如果所有的k个质心向量都不再发生变化，则聚类过程结束。

步骤3输出簇划分结果C={C1,C2,…,Ck}。

CalcWeights算法是由Nicholson等人[11]提出的,本文根据该算法原理进行调整，其基本流程如算法2所示。

算法2CalcWeights算法

输入：循环次数N,标签类型对应数量num,更新的标签集y1及聚类后的簇C。

输出：重新调整的标签集yw。

步骤1 forj=0 toNdo//N由数据集行数与设定的聚类次数共同决定

(1)计算第j类标签数numj在总数num中的占比:u=numj/num；

(2)计算缩放因子:multiplier=min (lg(|Cj|),2)；

(3)计算第j簇的标签分布。

步骤2计算每个数据样本xi(i=1,2,…,n)在各类标签中的权重结果,并存放在ins_weights[i]中。

步骤3将每个数据样本经过权重计算之后选取在各类标签中权重最大的作为该样本的标签；

步骤4输出最终的标签集合yw。

4 实验与结果分析

4.1 数据集与特征选取

为了检验本文所提方法适用性，本文选取具有代表性的入侵检测数据集NSL-KDD[12]和MOORE[13]进行实验，下面简单地对2个数据集进行介绍。

(1)NSL-KDD数据集。

NSL-KDD数据集是由Tavallaee等人[12]从KDDCUP99数据集中筛选而得的，作为改进的数据集，NSL-KDD在特征性能上更具有代表性。

该数据集拥有41维特征向量和1个被标记好的样本数据标签,其中有3个特征为字符型特征，分别为：protocol_type、flag和service。表1展示了该数据集的特征。

NSL-KDD数据集包括KDDTrain训练集和KDDTrain测试集，由于测试集与训练集的标签类型不相同，为了分析本文方法在带噪标签下的分类性能，因此只选取测试集作为本文实验的数据集。然而KDDTrain训练集有12种标签类型，每种类型数据差异较大，为了保证在注入不同比例噪声后不影响实验结果，选取实例数大于2 000的标签类型作为本次实验的对象，如表2所示。在对所选数据集进行预处理时，考虑到非数值型特征之间是否存在关联，本文在将其转换为数值型时使用one-hot编码，以保留属性中所携带的数学性质，即映射为(1,0,0),(0,1,0)和(0,0,1)的形式，一共有80个特征，最终41维特征向量转换成118维特征。此外，对剩余的38种数值特征采取标准方法进行等比例缩放，转换的公式为x′=(x-u)/σ,其中，x表示原始数据，u表示均值，σ表示标准差。最后随机选取数据集中70%的数据作为训练集，剩余30%作为测试集。

Table 1 Characteristics of NSL-KDD dataset表1 NSL-KDD数据集特征

Table 2 Six tag types with more than 2 000 instances表2 6个实例超过2 000的标签类型

(2)MOORE数据集。

MOORE数据集是目前应用最为广泛的网络流量分类数据集，它是由Moore等人[13]通过高性能网络监控器采集而得的，采集的数据分为10个数据流文档，一共377 526条数据，如表3所示,是相对较为完善的网络流特征集。

MOORE数据集的每种标签类型的数量比重差异很大，因此为了达到实验要求，同样选取实例数大于2 000的标签类型作为实验对象，如表4所示。由于MOORE数据集定义了248种网络数据流特征，为了避免MOORE数据集存在冗余现象以及分类相关性较小的特征，本文经过分析该数据集的特征，最终选取11种特征属性作为流量分类的特征，如表5所示。在选取分类特征后，仍然对数据集进行标准化处理，最后随机选取70%的数据作为训练集，剩余30%作为测试集。

Table 3 Ten document information of MOORE dataset表3 MOORE数据集10个文档信息

Table 5 Features selected in this paper for classification表5 本文选取的用于分类的特征

4.2 模型评价

本文将带噪标签的修复指标作为评判模型分类性能的关键，修复指标包括标签修复力度、模型输出结果质量和AUC。其中，标签修复力度是根据标签修复后的新标签与真实标签进行相似性对比来判定，本文使用调整兰德系数ARI(Adjusted Rand index)来计算标签修复力度。调整兰德系数是改进了的兰德系数，调整兰德系数假设模型的超分布为随机模型，即类和簇的划分为随机的，那么各类别和各簇的数据点数目是固定的。模型输出结果质量是指在校正的数据集上训练分类器,并在测试集上进行分类预测而获得的分类精度。本文在最终分类环节采用性能较优的随机森林分类模型计算分类的质量；AUC代表ROC曲线下覆盖的面积。由于ROC曲线的取值一般在0.5～1.0，值越接近1.0，检测的真实性就越高。

4.3 实验过程

本文选择Python作为编程语言，使用jupytyer-lab作为模型训练工具。首先对未添加噪声的NSL-KDD数据集和MOORE数据集直接使用随机森林进行分类。为了防止分类过程中出现欠拟合或过拟合现象，因此使用随机森林的学习曲线得到最佳n_estimators值，以降低实验的不合理性。n_estimators是随机森林的重要参数，表示森林中基评估器的数量,即树的数量。当n_estimators为181时，NSL-KDD数据集上的分类达到99.872%的准确率；当n_estimators为44时，MOORE数据集上的分类达到99.573%的准确率。随后在训练集中通过选取10%,20%,30%,40%,50%,55%,60%,65%,70%的数据将正确标签类型错误标注，错误标注的方式采取将正确标签错误分配和标签错误拼写来实现噪声的注入。随后将STC (Self-Training Correction)算法[14]、CC (Cluster-based Correction)算法[14]和ADE(Automatic Data Enhancement)算法[15]与随机森林算法相结合与本文方法进行对比，并使用上文提到的标签修复力度、模型输出结果质量和AUC来评估本本算法的性能。

4.4 实验结果

(1)标签精度。

不同算法的标签修复力度实验结果如图2所示，图中横坐标代表噪声比例，纵坐标代表算法修复力，即标签精度，图2a和图2b分别代表各算法在NSL-KDD数据集和MOORE数据集上的修复情况。将每种噪声比例下的修复值绘制成折线，可直观地看出不同噪声下各个算法的修复情况。

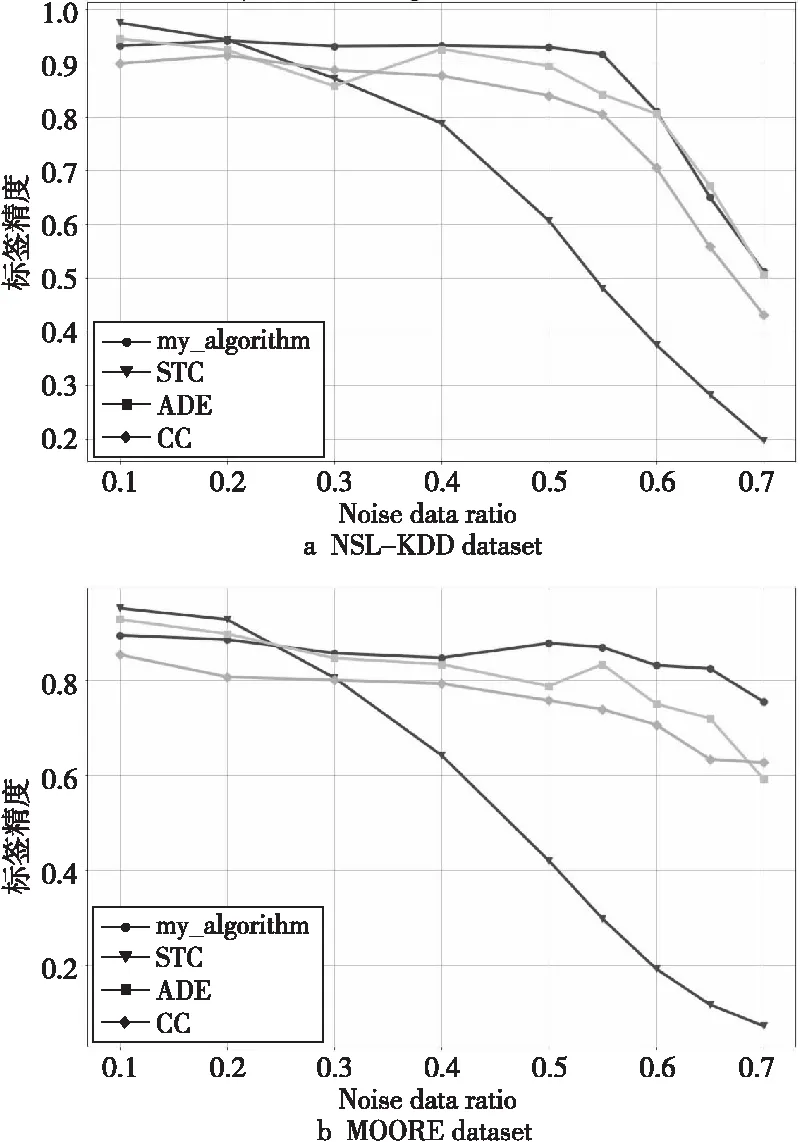
Figure 2 Repair power of each algorithm on NSL-KDD and MOORE with noisy data 图2 各算法在带噪数据集KSL-KDD 和MOORE上的修复力

由图2a可看出，对比修复算法STC在噪声比例不大于20%时具有较强的修复力，在最佳情况下比本文提出的算法、CC算法和ADE算法，分别高出0.043,0.075和0.030;而在MOORE数据集上，则分别高出0.057,0.098和0.023，但当噪声比例大于20%时，噪声修复力呈明显下降趋势,算法稳定性表现较差；当噪声比在20%～55%时，ADE算法、CC算法和本文提出的算法都具有较好的稳定性，并且在标签修复的精确率上本文的算法要比ADE算法和CC算法表现好一些，并在NSL-KDD数据集上表现最明显；当噪声比达到55%时，4种算法的修复力度都呈下降趋势，但整体情况本文算法的修复力度仍然要高于其他3种算法的。

(2) 模型输出结果质量。

模型输出结果质量通过使用经STC、CC、ADE和本文方法中的修复算法修复后的标签作为分类模型的输入，利用分类器对标签质量进行预测。图3展示了在NSL-KDD数据集和MOORE数据集上各算法的分类结果质量，图中横坐标表示当前标签所携带的噪声比例，纵坐标则表示最终分类准确率,即模型输出结果质量。

Figure 3 Classification results of each algorithm on KSL-KDD and MOORE with noisy data 图3 各算法在带噪数据集KSL-KDD 和MOORE上的分类性能

实验使用随机森林分别对带噪数据集与标签被修复的数据集进行分类后对比，可看出带噪数据集随着噪声比例的增加，分类准确率呈明显下降趋势，表明了标签噪声对分类器分类性能的危害是较严重的。前文提到，在有噪声的环境中，随机森林算法对含噪数据集具有一定的容忍性，因此本文选用随机森林算法作为4种修复算法的分类器，从理论上可得到较优的分类准确率。从图3可以看出，当噪声比例不大于20%时，STC算法相比其他3种算法具有更高的分类准确率；同时可观察到在NSL-KDD数据集上，在噪声比例达到15%左右时，本文提出的修复算法在最终的分类效果上要比ADE算法表现好，但在MOORE数据集上,当噪声比例不大于20%时，本文算法的分类性能比ADE算法的要低；当噪声比例大于20%时，STC算法的分类性能呈明显下降趋势，并且随着噪声比例增大，下降幅度也增加。此时本文提出的修复算法、CC算法和ADE算法在噪声比例到达55%之前都能使修复后的标签在分类性能上具有较好的稳定性。除此之外，本文的修复算法在标签修复后的分类准确率上要高于ADE算法的，在NSL-KDD数据集上同样表现最明显。而CC算法虽然也使修复后的标签保持着较好的分类稳定性，但在分类性能上略逊于这2种算法的；当噪声比例不小于55%时，4种算法所修复的标签在最终的分类器性能上都呈下降趋势。而在带噪的MOORE数据集上，本文提出的修复算法的分类性能表现较为稳定。整体上本文提出的修复算法在2个数据集上的总体性能都优于其他3种对比算法。

(3)AUC。

AUC指的是每个类型下的ROC曲线所形成的面积大小，由于网络流量一般属于多类别的数据集，因此将修复后的噪声数据直接训练得到的模型的平均AUC值,作为该模型的AUC性能指标。图4展示了4种算法在不同噪声比例下在2个数据集上的AUC指标情况。由图4a可看出，在噪声比不大于20%时,STC算法的AUC仍然略高于本文算法的AUC，ADE算法的AUC整体低于上述2种算法但高于CC算法的AUC；当噪声比例大于20%时，STC算法的AUC开始呈明显下降趋势，此时本文算法相比ADE算法和CC算法有更高的稳定性；当噪声比例不小于60%时，4种算法的AUC值都呈下降趋势，并且在NSL-KDD数据集上呈现得较为明显。

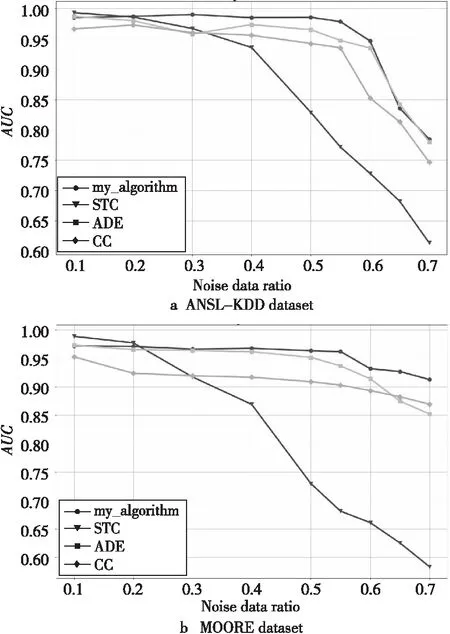
Figure 4 AUC values of each algorithm on KSL-KDD and MOORE with noisy data 图4 各算法在带噪数据集KSL-KDD 和MOORE上的AUC值

(4)运行时间。

图5为修复算法运行的时间对比结果。从图中可以清晰地看出，本文所提算法和CC算法在NSL-KDD数据集和MOORE数据集上所消耗的时间都呈现较好的稳定性，计算时间分别在1 s～4 s和在2 s～7 s。STC算法和ADE算法在2个数据集上所耗费的时间大体随着噪声比例的提升有一定的增加，其中ADE算法在2个数据集上的计算时间都高于其他3种算法的，在NSL-KDD数据集上耗时最高达到了256.49 s左右，在MOORE数据集上计算耗时达到88.06 s左右。

Figure 5 Calculation time of each algorithm on KSL-KDD and MOORE with noisy data 图5 各算法在带噪数据集KSL-KDD 和MOORE上的计算时间

由于本文在预处理阶段从NSL-KDD数据集和MOORE数据集中选取的特征数量不同，NSL-KDD数据集在预处理后得到118维特征，其中有80维是由原特征中的字符特征转换而得的，MOORE则根据实验需求选取11维特征。因此，猜测不同的算法计算耗时可能会受到数据集维度的影响，其中，ADE算法受到维度过高时的影响较大，当维度减小时，其所耗费的时间也明显减少；STC算法的计算时间也会根据维度的减小而减少。但是，无论如何，本文所提出的算法相对其它三者都呈现出更好的稳定性，对不同维度的数据集具有一定的适应性和稳定性。

5 结束语

本文提出的基于标签噪声修复的网络流量分类方法，是根据不同类型噪声对采用的权重算法进行改进，实现对正确标签错误标记和标签的错误拼写2种情况的标签修复。本文在2个网络流量数据集上验证了本文算法的合理性和稳定性，与其他文献中的标签修复算法对比结果表明，本文所提修复算法能更好地对含不同比例噪声的数据集进行修复，并在最终的分类结果上保持较好的性能，有更好的执行效率、稳定性、精确度和适应性。