小信号放大电路任意波形THD全自动测量系统研究*

桂 丹,喻宗杰

(1.华中科技大学武汉光电国家研究中心，湖北 武汉 430074；2.武汉软件工程职业学院电子工程学院，湖北 武汉 430205; 3.烽火通信科技股份有限公司，湖北 武汉 430205)

1 引言

小信号放大电路是模拟电路中常见的设计电路，信号的放大效果直接影响电路的整体性能。因此，小信号经过放大后的信号失真度对于后续信号的采样、数据处理等起着非常关键的作用。目前，小信号放大电路的常见设计包括单管放大电路、集成运算放大器和功率放大电路等。然而，模拟电路由于其信号弱，精度不够，理论与实践差距较大等问题，严重影响着信号的准确提取及应用[1]。尤其对于音频信号，传统的语音质量测量方法相对主观，同时面临成本高、开发周期长和测试过程繁琐等困境。

在微电子与计算机领域，考虑到实用性、开发成本及便携程度等因素，小信号放大电路一般是由放大元器件、模拟开关等基本元件的组合电路来实现,但因小信号的放大受频率、幅值、噪声、增益和阻抗等影响，容易形成性能干扰,造成最终放大后的信号完整性难以保证，导致信号失真程度不易判断。晶体管放大器电路理论设计与仿真结果及实际测试指标常存在误差，与实际电路元件特性非理想和分布参数导致寄生振荡等问题相关[2]。

传统检测信号放大后失真程度的仪器，一方面存在体积较大、机身笨重等问题，在实验室或机房等测试环境下还可以适应，一旦到户外或测试环境受限的场所就困难重重。而且，针对不同的测试方法，还需配备频谱仪、示波器等辅助测量工具，整体测量成本及空间占用问题不可忽略。另一方面繁琐的仪器连接及分析过程，对专业度有一定的要求，那么，对于专业基础相对欠缺的工作人员实用性会大打折扣[3]。因此，开发一种操作简单、调节方便、一键式流程、独立显示、小型化的快速自动计算总谐波失真THD(Total Harmonic Distortion)度的装置及配套软件，实现小信号放大电路任意波形输出的THD值自动识别及测量，对电路设计人员实时观测电路实际状况具有重要意义。

为高精度测量放大信号的失真度，本文采用快速傅里叶变换FFT(Fast Fourier Transform)算法，对放大后的信号进行模数转换ADC(Analog-to-Digital Converter)并采样。对输入信号为1 kHz的小信号，以500 Hz为基准，提取256个离散点，然后利用离散傅里叶变换DFT(Discrete Fourier Transform)的共轭对称性，最终以128个点为采集数据，进行FFT运算，在保证精度的同时，降低单片机的计算量和存储空间，以保证测量系统快速地得出结果[4]。小信号放大电路的失真度测量系统以 stm32f103c6单片机为运算控制核心，实时识别并显示当前输出波形的类型及THD值，以便电路设计人员快速准确地判断放大电路的信号状态。经Multisim电路仿真，由虚拟失真度测试仪测量出当前放大电路的THD值，和小信号放大电路任意波形THD自动测量系统在OLED屏幕上实际显示的结果进行对比，验证了本文设计的小信号放大电路失真度测量系统的实测结果与电路仿真结果接近。

2 测量系统分析与设计

理想情况下，信号经过放大、传输等过程不会发生改变。但是，由于元件非理想、分布参数导致寄生振荡及信道中各种干扰等，信号在实际中不可能理想放大和传输，多少会发生畸变，出现信号失真。信号失真分为线性失真和非线性失真。非线性失真也就是常说的谐波失真，信号经过非线性信道产生的新频率分量，使得输出信号的频率不再是单一的原频率，而是包含了二次、三次及多次谐波分量的频率组合，这些多余出来的谐波成分与实际输入信号的比值，通常被用来计算总谐波失真。对于音频信号，这种失真对最终信号质量的影响非常大，也是衡量音频电子产品设计优劣的重要指标。

从测量失真度的原理来讲，根据测量过程中新频率分量是直接还是间接得到，测量方法分别采用谐波分析法和基波剔除法。谐波分析法需要获得各谐波分量的幅值，该方法利用频谱分析方法选频，可得出基波和各谐波分量，从而计算出失真度。基波剔除法则通过选频网络(比如电桥、陷波网络等)抑制基波，将其从整个信号中剔除，由原信号和基波抑制后的信号功率来计算出失真度。由于其测量过程中需提供无失真信号，测量范围为1 Hz～1 MHz。而剔除基波的过程中还有噪声存在，计算结果因此也会受到影响。对于低频信号测量误差达5%～30%，对于音频信号来讲，这种方法就不适用了[5]。而谐波分析法一般借助数字或模拟的方式选频得到基波和各谐波的能量，利用离散傅里叶变换、谐波计算公式近似等方法，可快速计算出总谐波失真值。测量系统的性能主要取决于模拟信号到数字信号转换的精度及数据处理算法的可靠程度。因此，谐波分析法的测量系统在设计时需综合考虑以上指标来选择合适的硬件及软件。同时，谐波分析法由于其测量系统的硬件结构相对简单，且计算速度快和精度高等优势，已成为常用的信号失真度检测方法。

小信号放大电路任意输出波形全自动THD测量系统，以谐波分析法为理论基础，结构上分为晶体管放大电路和单片机采样计算2部分，如图1所示。

Figure 1 Structure of the THD measurement system图1 总谐波失真测量系统结构图

理论上，任何连续测量的时域信号都可以表示为不同频率的正弦波信号的无限叠加，以累加的方式来计算该信号中不同信号的频率、振幅和相位。总谐波失真的定义：输入为正弦信号时，其非线性失真表现为输出信号中出现谐波分量，如果输入电压如式(1)所示：

ui=Uimcosωt

(1)

其中，ui为输入瞬时电压，Uim为输入电压最大值，ω为角频率。

含有非线性失真的输出交流电压如式(2)所示：

uo=Uo1cos(ωt+φ1)+Uo2cos(2ωt+φ2)+

Uo3cos(3ωt+φ3)+…+Uoncos(nωt+φn)+L

(2)

其中，n为谐波分量的个数，Uo1～Uon为各谐波分量的电压最大值，φ1～φ2为各谐波分量的初相，L为直流分量。

则有式(3)：

(3)

为了方便计算，取前5次谐波，可得式(4)：

(4)

因此，本文设计的全自动THD测量系统使用FFT算法来得到各谐波分量有效值，然后由二次、三次、四次和五次谐波分量均方根与基波的比值自动计算出放大电路的总谐波失真(THD)值[6]。

由于音频放大器放大了人类听到的信号，考虑到人类听觉的心理声学，人类通常无法检测到失真度低于1%的信号，而失真度超过10%的信号又会有明显的失真。人类的灵敏度取决于频率，对高阶失真也更敏感。通过训练某些类型的失真，可以听到一些低至0.3%的失真效应。也就是说，总谐波失真(THD)值越小，信道的非线性失真越小，信号就越纯净。同时，在设计音频放大器时还需考虑成本，信号频率是否低于人类听觉阈值，权衡成本与收益。因此，一般设计音频电子产品时THD值需小于或在1%附近，这个数值越小，表明该电子产品的品质越高。THD值在电子产品信号检测方面具有非常重要的意义[7]。

理论分析和电路仿真表明，对于信号源输出的1 kHz的正弦信号，总谐波失真的近似值越小，表示放大电路的信号失真测量越精准，THD基本在1%以内。对于信号源输出的1 kHz的方波信号，总谐波失真的近似值大约是38.87%(前5次谐波计算的近似值)。现实中，被测信号是一个包含基波和各次谐波分量的周期失真正弦波，其表达式如式(5)所示：

(5)

其中，ω0为角频率，A0～An为傅里叶系数，其傅里叶级数展开如式(6)所示：

(6)

(7)

将式(6)和式(7)代入式(4)可得：

(8)

从式(8)可知，通过对信号进行离散傅里叶变换 DFT，求各级傅里叶级数，得出信号在各阶的谐波有效值，可计算出总谐波失真。本文进一步对离散傅里叶级数进行抽样，利用快速傅里叶变换，在保证精度的前提下，加快计算速度。基于此理论，设计单片机的波形失真度测量程序，自动计算出多次谐波分量均方根与基波分量的比值，最终得出THD值。

测量放大电路失真度的系统主要包括2大部分：(1)由多级晶体管放大器、模拟开关和阻容元件组成的放大电路。为实现多种不同失真波形的识别与读取，该部分包括了二级放大、三级放大等多级级联电路，还包括推挽电路以形成无明显失真、消底失真、消顶失真、双向失真和交越失真5种常见输出波形。(2)以stm32f103c6单片机为核心的测量部分。将小信号放大电路的输出连接到stm32f103c6单片机的高频ADC采样进行FFT运算，准确提取离散点的有效值，并将计算后的结果在线显示到OLED屏上。将信号输出端引到示波器，实时显示当前波形状态。总谐波失真(THD)测量系统框图如图1所示。

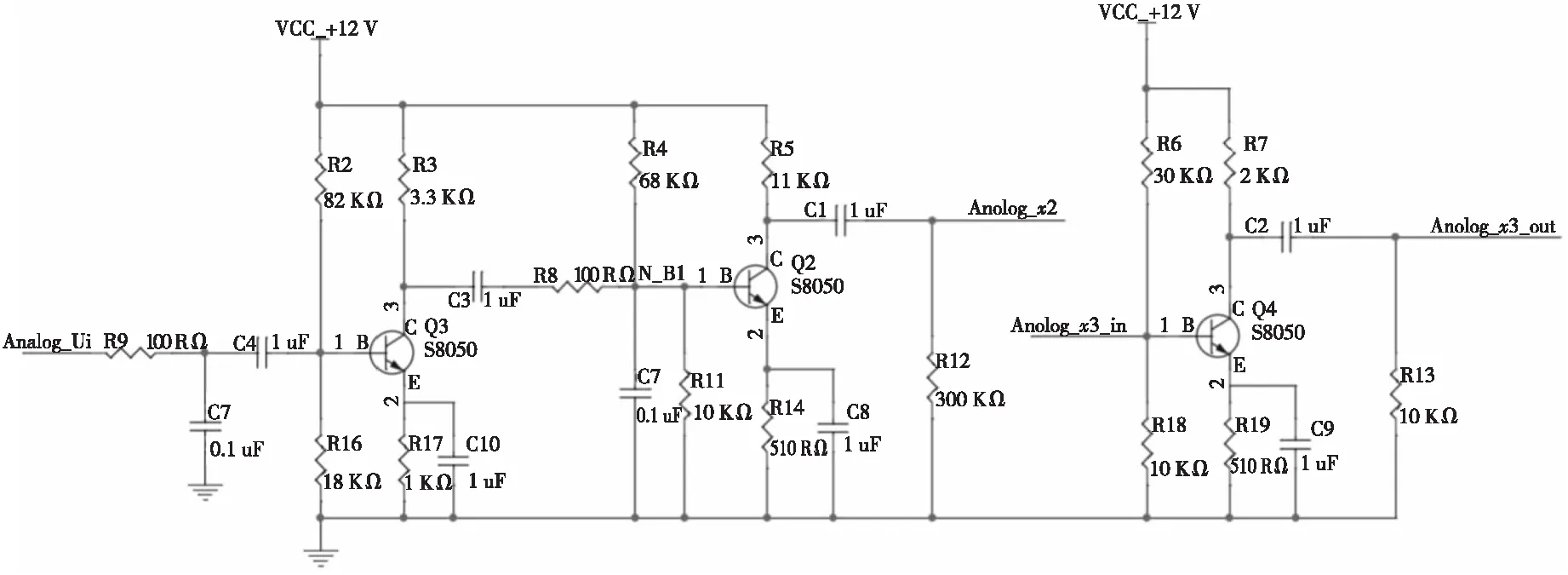
Figure 2 Part circuit schematic diagram in transistor amplifier circuit图2 晶体管放大电路部分电路原理图

2.1 小信号放大电路

晶体管放大电路由模拟开关、晶体管和阻容元件等元件组合而成，通过合理设计电路，尤其是针对单管放大电路静态工作点的设置，经过一级放大、二级放大和三级放大，实现输入小信号(20 mV)到输出峰峰值在2 V以上的输出波形，满足单片机ADC采样基本需求。针对不同原因造成的失真，单片机进行高频采样并识别波形，在满足精度要求的同时，减少了需要存储的离散点数，提高了失真度测量系统的工作效率。部分电路原理图如图2所示。

晶体管放大电路的波形失真与静态工作点设置、输入信号幅值等因素相关，需要针对不同波形输出需求进行相应设置。常见波形有5种，分别是无明显失真、底部失真、顶部失真、双向失真和交越失真。

(1) 无明显失真。

无明显失真的状态为：静态工作点设置合理，三极管工作在放大状态。设置步骤为：调节二级放大三极管基极与地之间的电阻大小，使发射结正向偏置，集电结反向偏置三极管处于放大工作状态，出现无明显失真波形。

(2) 底部失真。

底部失真的状态为：静态工作点偏高，三极管工作在饱和状态，输入信号负半周正常放大，正半周畸变。设置步骤为：调节二级放大三极管基极与地之间的电阻大小，使发射结正向偏置，集电结正向偏置三极管处于饱和工作状态。输出波形负半周畸变，正半周正常放大，出现底部失真波形，

(3) 顶部失真。

顶部失真的状态为：静态工作点偏低，三极管工作在截止状态，输入信号负半周畸变，正半周正常放大。设置步骤为：调节二级放大三极管基极与地之间的电阻大小，使发射结反向偏置。三极管处于截止状态。输出波形出现负半周正常放大，正半周畸变，出现顶部失真波形。

(4) 双向失真。

双向失真的状态为：静态工作点设置合理，但输入信号幅值较大，三极管既有饱和状态也有截止状态。设置步骤为：调节放大器处于二级放大或三级放大，达到较高的放大倍数，出现双向失真。

(5) 交越失真。

交越失真的状态为：交越失真与三极管的导通电压相关，输入电压较小，低于晶体管门限电压，导致三极管截止。设置合适的静态工作点，三极管处于微导通。利用二极管和电阻的压降产生偏执电压是解决交越失真较为常用的方法。设置步骤为：通过调节继电器短接功率放大器2个三极管基极，出现交越失真。

2.2 总谐波失真计算

总谐波失真THD是衡量线性放大器非线性失真程度的常用手段，其非线性失真表现为输出信号中出现谐波分量。现实中有硬件和软件2种方式实现THD值的自动测量。

从硬件角度来实现时，输出波形的一路信号经陷波电路滤除基波分量，有效值检波后送入单片机内部的ADC采样得有效波X1，另一路信号直接通过有效值检波送入单片机内部的ADC采样，所得有效波为X2，采样得到的2个有效值比值即为谐波失真率，即THD=X1/X2。

Figure 3 Matlab simulation diagram of FFT operation图3 FFT运算的Matlab仿真图

Figure 4 Simulation waveform of a circuit without significant distortion图4 无明显失真电路仿真波形

从软件角度来实现时，单片机对采集到的波形进行ADC采样和FFT运算，取每阶的有效值，共取5阶，对第2阶到第5阶的有效值即Uo2～Uo5进行均方根运算，其结果与基波谐波分量Uo1的比值即为总谐波失真值。本文采用软件实现的方法，不仅电路简洁，方便调试，而且成本也低。

本文利用单片机stm32f103c6进行信号采集及运算，放大后的波形经ADC高频采样，此时的采样点数可以是1 024，512和256等，出于对系统成本、单片机运算量、存储空间及效率等多方考虑，本文以1 kHz为基准，提取256个离散点，利用离散傅里叶变换的共轭对称特性，最终采样128个点，进行快速傅里叶运算，得到各谐波分量有效值。提取前5次谐波分量值Uo2～Uo5的有效值进行均方根运算，并以该结果与Uo1的比值作为THD值[8]。在终端配合OLED屏幕，在线显示当前计算结果，实时读出当前状态下波形的失真度并告知失真波形类型，便于电路设计人员准确判断信号状态。

在进行仿真测量之前，先以Matlab仿真验证FFT运算的正确性。在0～1 200 Hz内，拟提取0 Hz，200 Hz，800 Hz和1 000 Hz的谐波分量，如果结果在对应位置提取，则FFT运算程序设计正确，如果不在或偏差较大，则表示程序设计有误，Matlab仿真结果如图3所示。由图3可知，提取位置准确，可依此进行谐波分量的均方根运算，并由该结果与基波的比值计算出THD值。

3 仿真信号测试及分析

将虚拟仿真测试仪器连接到小信号放大电路的各级，设置输入正弦波的峰峰值为20 mV，频率为1 kHz，虚拟示波器接信号输出端，并同时引出失真度测试仪，实时读取THD值。与实际设计的小信号放大电路THD自动测量系统的显示结果进行对比，得出信号失真度测量的准确程度，以判断小信号放大电路的设计合理性和单片机FFT运算的准确度。虚拟仿真测量的所有波形如图4～图8所示。

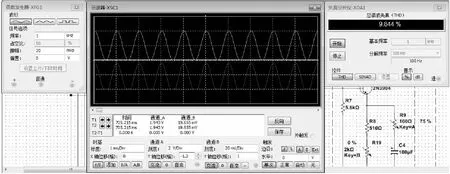
Figure 5 Simulation waveform of a circuit with bottom distortion图5 底部失真电路仿真波形

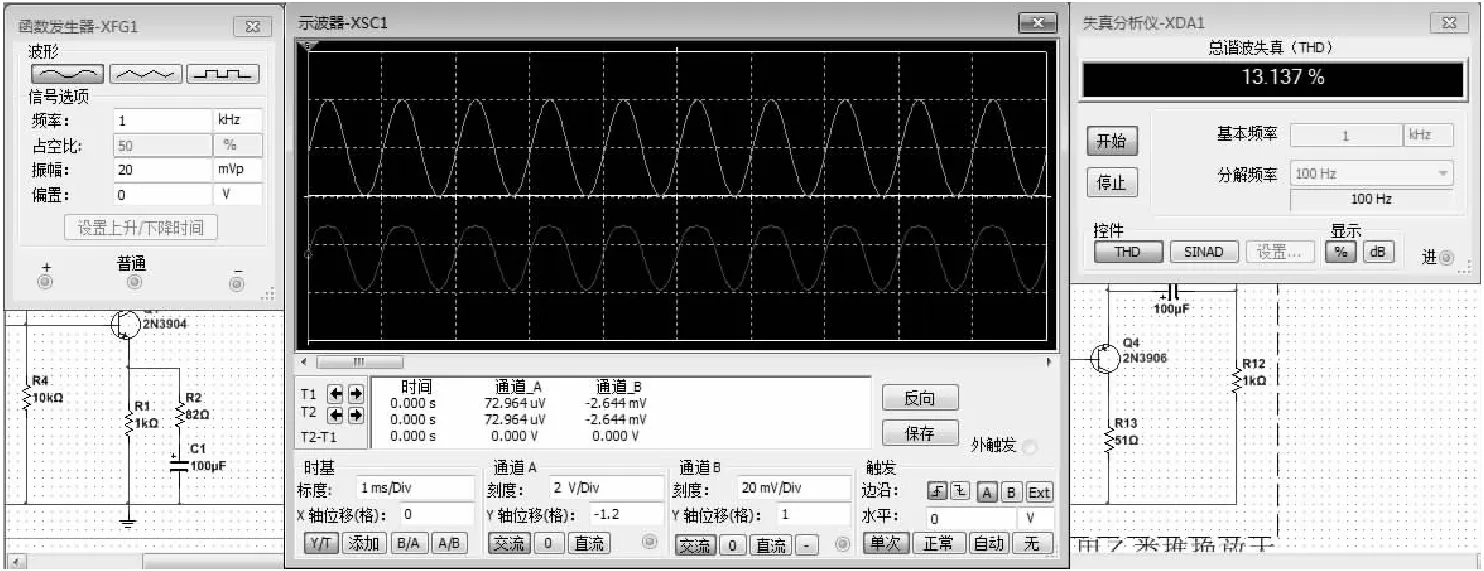
Figure 6 Simulation waveform of a circuit with top distortion图6 顶部失真电路仿真波形

Figure 7 Simulation waveform of a circuit with bidirectional distortion图7 双向失真电路仿真波形

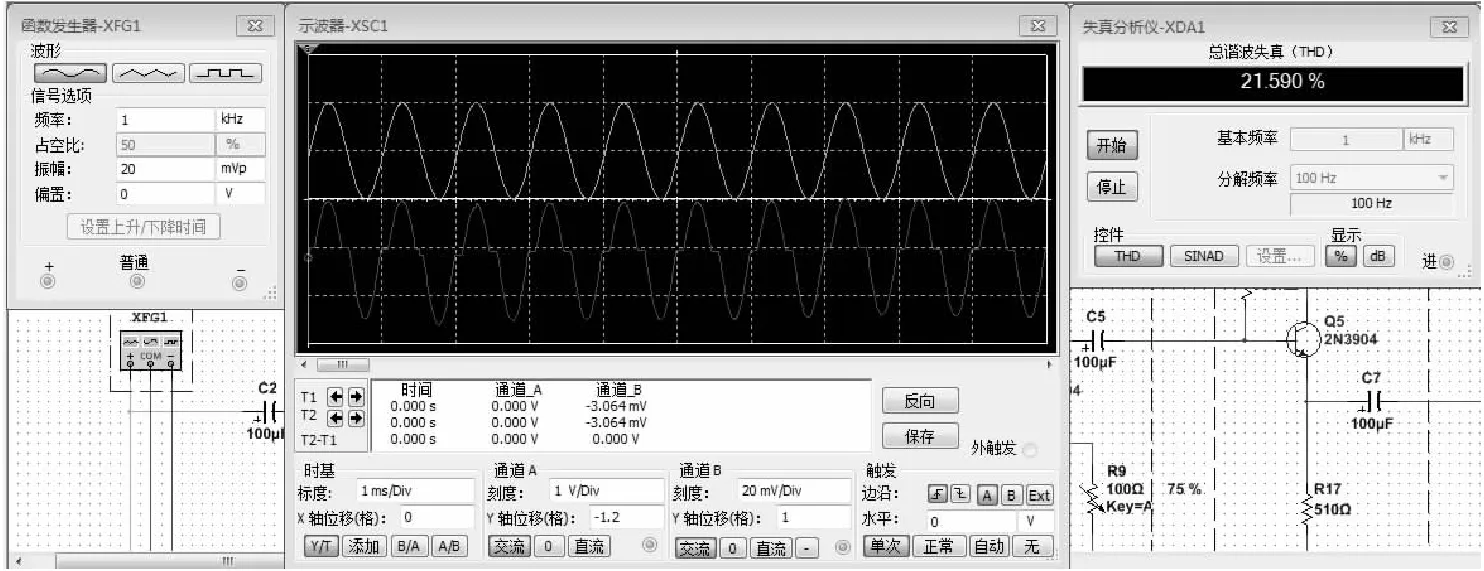
Figure 8 Simulation waveform of a circuit with crossover distortion图8 交越失真电路仿真波形

从图4～图8可以看出，无明显失真波形，也就是常说的正常波形，其理想情况下的THD值在1%附近，顶部失真波形和底部失真波形的THD值约为10%，交越失真波形的THD值在20%左右，而双向失真波形的失真度受输入信号影响较大，其THD值的范围也较大。

4 电路测试与分析

4.1 实物测试

本节以正常波形(无失真波形)为例，给出实物测试结果，如图9所示。信号发生器输入频率为1 kHz，峰峰值为20 mVpp的正弦波至小信号放大电路，测量系统的按键切换到1号位置(图9板卡左侧位置)，单片机自动计算出THD值并显示到OLED屏上。

Figure 9 Physical test diagram of normal waveform THD value图9 正常波形THD值实物测试图

4.2 环路测试

将开关拨至2，输入信号设置为2Vpp，改变电路结构。原电路结构为：输入小信号经过放大电路，得到的结果输入单片机进行采样及计算。改变后的电路结构为：输入信号直接输入到单片机进行采样及计算。环路测试的目的是为了验证小信号放大电路THD测量系统的准确性。测量系统正常工作情况，开关直接拨至1即可。经正弦波、三角波和方波测试，小信号放大电路实测的THD值分别为1.351%，10.899%和42.902%，如图10所示。与仿真电路测试结果接近，方波情况稍有差异，将在误差分析部分具体描述[9，10]。

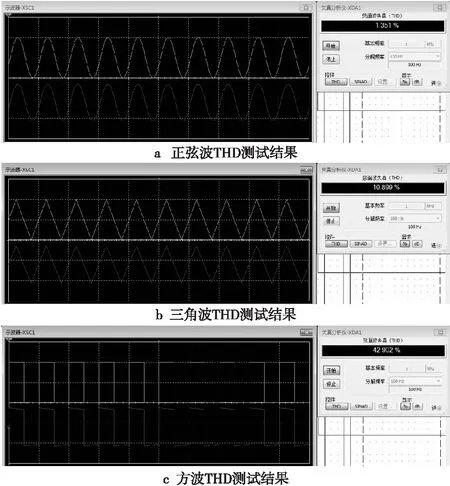
Figure 10 THD test results of three waveforms图10 3种波形的THD测试结果

4.3 误差分析

电路经过晶体管放大电路和直接接入单片机2种情况下，下面分别进行FFT运算的结果对比：

正弦波的失真度分别为1.351% 和0.739%；三角波的失真度分别为10.406%和11.201%；方波的失真度分别为42.002%和38.412%。此结果表明，晶体管放大电路放大小信号过程中，存在一定程度误差，但是误差范围在0.1%左右，可满足普通电子产品关于信号失真度测量的基本要求，能够作为测试仪器提供商业应用。需要说明的是，对于方波，由于方波是取前5次谐波分量的计算结果，为38.412%。如果是取前7次计算结果，THD值约为42%，与小信号放大电路失真度测量结果的42.002%几乎无差。此结果与FFT运算取的阶数越多，精度越高，结果越接近理论值。可见，此测量系统可高精度地自动计算出任意输出波形的总谐波失真。操作简便，显示清晰,误差可控,系统性能指标良好[11,12]。

5 结束语

小信号放大电路任意波形THD全自动测量系统，通过对低频小信号进行电压放大、高频ADC采样和FFT运算提取各谐波分量的有效值等操作，实现高精度快速波形识别和THD值测量。经Multisim仿真及实物测试表明，以晶体管、模拟开关等放大电路组成的小信号放大电路，电路理论设计完整，放大倍数可控，精确度高，较集成运算放大器组成的放大电路具有更好的可调控性；以stm32f103c6单片机为核心的全自动波形识别及THD测量系统，高效实时，利用离散傅里叶变换的共轭对称性，以快速傅里叶变换将信号采集量从1 024降低到128，在几乎不影响波形检测精度的情况下，有效减少了存储压力和计算量。测量系统识别准确，总谐波失真计算值与环路测试结果接近，误差在1%以内，满足高精度失真度测试仪器标准。体积小便携，一键式设计使操作简单，显示清晰，具备良好的实用价值。