全阴影卫星信道高效硬件数字孪生方法

房 晨，赵子坤，张 宁，柳 涛，朱秋明，毛通宝，毛 开

(1.南京航空航天大学 电磁频谱空间认知动态系统工业与信息化部重点实验室，南京 210016； 2.国家无线电监测中心乌鲁木齐监测站，乌鲁木齐 831400)

0 引 言

卫星通信具有组网灵活、可实现全球覆盖的优点，是未来空天地一体化通信网络的重要组成部分[1]。卫星信道作为卫星通信的传输媒介，由于同时存在传播损耗和时延、多径效应以及阴影衰落，严重影响了数字信号传输的可靠性，已成为当前通信领域的研究热点之一。利用实际卫星链路进行试验成本昂贵，并且测试环境单一，测试结果不全面且准确度低。相比之下，采用数字孪生技术将卫星通信的物理信道映射到数字空间，是在实验室环境下进行卫星通信系统物理级或链路级的性能评估的一种有效方法[2-3]。

在卫星通信系统中，由于卫星应答器与地面终端之间的距离较远，多径衰落和阴影效应严重影响了卫星通信的通信质量和系统的频谱效率。常用的卫星衰落信道模型包括Suzuki，Corazza，NLN以及Lutz等[4-7]。其中，Suzuki，Corazza和NLN模型在软硬件仿真实现时比Lutz模型更加简单。由于这三种信道衰落模型都与阴影衰落有关，又统称为全阴影卫星信道衰落模型[8]。

全阴影卫星信道模型的硬件孪生复现的关键在于复高斯序列的模拟。最传统的方法是基于查找表(Look Up Table, LUT)方法，其实现原理简单，但需要大量的随机存储器(Random Access Memory, RAM)资源[9]； 坐标旋转数字计算(Coordinate Rotation Digital Computer, CORDIC)算法是另一种低成本的硬件实现方案[10]。文献[10-12]提出了基于传统CORDIC算法的信道模拟方法，但需要较多的迭代运算，存在很长的延迟，影响系统的实时性。为了减少迭代次数，文献[13-14]提出了一种高基数算法，但其硬件电路复杂，不易实现。

本文提出了一种基于现场可编程门阵列(Field Programmable Gate Array, FPGA)的全阴影卫星信道衰落的通用硬件架构，该方案基于调频信号叠加(Sum of Frequency Modulation, SoFM)原理[15]，采用迭代算法实现复高斯序列，通过CORDIC算法[16]实现信道衰落中初等函数的硬件实时计算。此外，本文还分析了硬件输出信道衰落的实测结果，包括幅值分布、定点化增益以及频谱形状等，与仿真结果进行对比分析，验证了本文方法的正确性。

1 全阴影卫星信道模型

电磁波在传播过程中，到达接收端的信号通常由多条具有不同时延和入射角度的路径叠加而成，包括直射路径分量和受到反射、折射以及障碍物衍射等影响的散射路径分量。由于受到山脉、楼宇等遮挡导致的阴影衰落，在不考虑信道噪声时，全阴影卫星信道冲激响应可以表示为

(1)

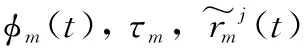
(2)

(3)

2 基于FPGA的卫星信道数字孪生

2.1 基于迭代算法的复高斯变量模拟

基于随机变量分解思想，上述三种全阴影卫星信道衰落的离散化表达式可由相互独立的复高斯序列组合或非线性变换表示。Suzuki衰落可表示为[10]

(4)

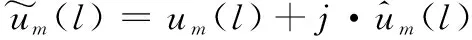
Corazza衰落可表示为[2]

(5)

式中：ρm,fm,θm分别为直射径的幅值、多普勒频率和随机初始相位。

NLN衰落可表示为[6]

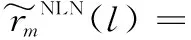
(6)

式中：2q为相互独立的同相分量数目。

全阴影卫星信道模拟的关键在于复高斯变量的产生，本文采用改进的调频谐波叠加方法实现连续相位的离散复高斯序列，为了便于FPGA定点化实现，复高斯序列离散化模型可表示为[15]

(7)

模拟复高斯序列的关键在于产生大量的复指数信号，目前大多采用LUT方法或CORDIC算法。其中，LUT方法需要把频率值以及正余弦信号的幅值表存于RAM中，再通过相位累加得到查找表地址，利用地址和幅值映射关系产生。LUT方法易于硬件实现，但是随着模拟的路径数以及衰落类型复杂度的提高，会受限于硬件中的RAM资源。CORDIC算法消耗RAM资源较少，但需要对相位值迭代运算，影响系统的实时性。为解决该问题，本文提出了一种基于迭代思想的产生算法，利用复指数信号前一时刻值，便可以通过迭代得到下一时刻的值，可大大减小硬件存储资源[17]：

(8)

图1给出了基于迭代算法的复指数信号硬件实现框图，选择器读取ROM表中预存的迭代因子，通过复数乘法器实时计算出下一时刻的迭代值。此外，该方案还结合时分复用思想，采用串行架构，进一步减少系统资源需求。

图1 基于迭代方法的复指数硬件实现Fig.1 Hardware implementation of complex exponent based on iterative method

2.2 基于CORDIC的非线性变换实现

经典CORDIC算法的核心思想是将所需的角度划分为一组固定角度的集合，通过有限数目的旋转，实现时变相位映射为一组角度集合的线性组合过程。CORDIC算法有旋转和向量两个模式，图2给出了旋转模式的双曲坐标系示意图。

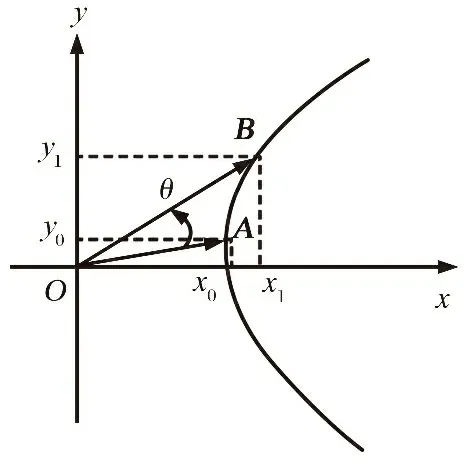
图2 双曲坐标系旋转模式Fig.2 Rotation mode of hyperbolic coordinate system

在双曲坐标系下，将初始二维向量A(x0,y0)逆时针旋转角度θ得到B(x1,y1)。其变换关系可用矩阵表示为

(9)

提取公因子coshθ，式(9)改写为

(10)

双曲坐标系旋转过程，旋转角度θ可表示为满足近似关系为tanhθi≈2-i的一组角度集合{1≤i≤L-1∣θi=artanh(2-i)}，其中:L为定点化数据位宽长度；i为当前迭代的次数。同样的，可以通过移位和加减操作完成双曲正余弦函数值的计算，旋转过程可以表示为

(11)

式中：zi为剩余的旋转角度；di为旋转方向因子，为±1。需要注意的是，对于双曲坐标旋转过程，迭代次数i需要满足kn(kn=3kn-1+1,k1=4,n∈Z+)才可以保证迭代具有收敛性，即从第四次迭代开始，重复迭代的位置分别为：i=4, 13, …, 3k+1, …。当zn→0时，双曲坐标旋转模式下最后迭代的输出xn,yn可表示为

(12)

图3给出了基于CORDIC算法的幂指数和平方根函数的硬件实现框图，第一级流水线首先对系统设定x,y,z的初始值，系统复位之后，对x,y,z寄存器进行初始化。在幂指数函数生成模块中，初始值分别为1，0，θ； 在平方根函数生成模块中，初始值分别为θ+1，θ-1，0。然后，利用移位寄存器实现乘以2-i运算。从第二级流水线中，通过判决器判断剩余角度的极性从而得到本级流水线中迭代旋转因子的符号，进而完成第n级流水线的运算。最终针对两种不同的函数，对xn,yn分别进行相加和乘以补偿因子Kn，得到输入角度的e指数与平方根函数值。

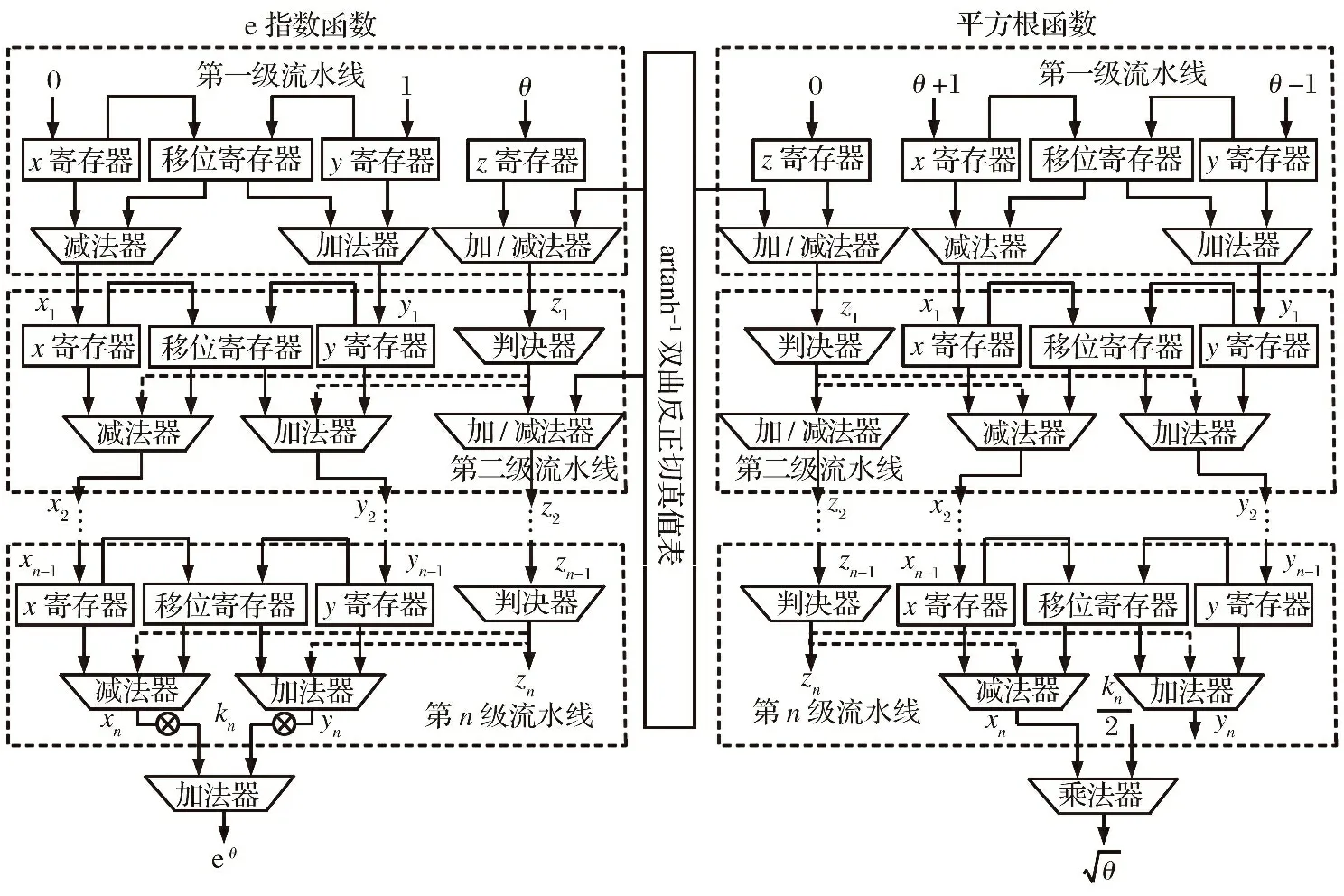
图3 幂指数/平方根函数硬件实现框图Fig.3 Exponential and square root function hardware implementation block diagram

2.3 全阴影卫星信道硬件数字孪生

图4给出了本文全阴影卫星信道衰落模拟的实现方案，每条多径的参数可由用户配置，并通过PCIE总线由PC端下发到FPGA中。根据各个全阴影卫星信道衰落的表达式，上述信道衰落可由复高斯序列经过非线性变换组合而成，本文复高斯衰落序列的产生基于时分复用思想，采取串行架构的设计，通过基于迭代的复指数信号产生模块在低速率Fs1=100/NMHz下生成N根复指数信号，采用N=64根射线叠加，再通过累加器与内插滤波器把叠加生成的复高斯序列内插到系统时钟100 MHz，最终得到系统时钟下的复高斯序列。

图4 全阴影卫星信道衰落产生框图Fig.4 Block diagram of full-shadow satellite channel fading generation

在此基础上，利用每个衰落对应的非线性变换公式，通过采用一些乘法器、累加器、加法器和基于CORDIC算法实现的幂指数函数和平方根函数产生模块, 可以实现全阴影卫星信道衰落的模拟。本文还扩展了生成全阴影卫星信道衰落过程中所需要的Rayleigh，Rice，Nakagami衰落以及阴影衰落。最后通过数据选择器输出，根据用户输入的信道衰落类型，从而生成相应的信道衰落。

3 硬件实测及分析

3.1 硬件资源消耗

为了验证提出的基于迭代算法与CORDIC算法的全阴影卫星信道衰落硬件生成方法的效率，基于Xilinx XC7K325tffg900 FPGA芯片对信道衰落进行了硬件实现。表1总结了针对复高斯序列产生模块各个方法的硬件资源消耗以及与FPGA上可配置资源对应的比率，其中，系统时钟为100 MHz，定点化数据位宽为16位。与LUT方法相比，本文算法的块存储器的使用率从3.82%降低到了0.22%，性能提升显著。相较于CORDIC算法，LUT和寄存器的消耗率则分别减少了2.46%和2.32%。整体资源使用率与两种方法相比，分别降低了6.21%和5.23%，硬件资源利用率大幅提升。同时，通过硬件仿真比较了各个方法的运算延迟，即系统下发参数到复高斯序列输出所经过的时间延迟，本文算法仅为7个时钟周期，因而更适合卫星信道的实时模拟。

表1 复高斯序列产生模块的硬件资源消耗Table1 Hardware resource consumption of complex Gaussian sequence generation module

3.2 实测结果分析

为验证全阴影卫星信道数字孪生方法的正确性，对硬件模拟输出的各种信道衰落分别进行了测试，设定4条具有不同多普勒频移的多径信道。图5给出了阴影衰落(Lognormal), Suzuki, Corazza和NLN四种全阴影信道衰落的理论仿真和硬件实测结果的频谱图，其中多普勒扩展为2 kHz，对应的频移分别为5 960 Hz, 13 100 Hz, 19 000 Hz和26 800 Hz。由图可以看到硬件输出频谱与仿真结果基本吻合，验证了本文模拟方法的有效性。

图5 全阴影卫星信道衰落多普勒功率谱Fig.5 DPSDs of full-shadow satellite channel fading

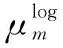
图6 全阴影卫星信道衰落概率密度函数Fig.6 PDFs of full-shadow satellite channel fading

表2进一步比较几种全阴影信道衰落输出的均值和方差，包括浮点计算的理论均值和方差、16位定点硬件模拟的实测均值和方差。其中，理论与去除定点化数据影响的实测均值和方差的平均相对误差为2.54%，最大误差为5.81%，最小误差为0.58%，进一步验证了信道模拟方法以及全阴影卫星信道模拟复现的正确性与有效性。

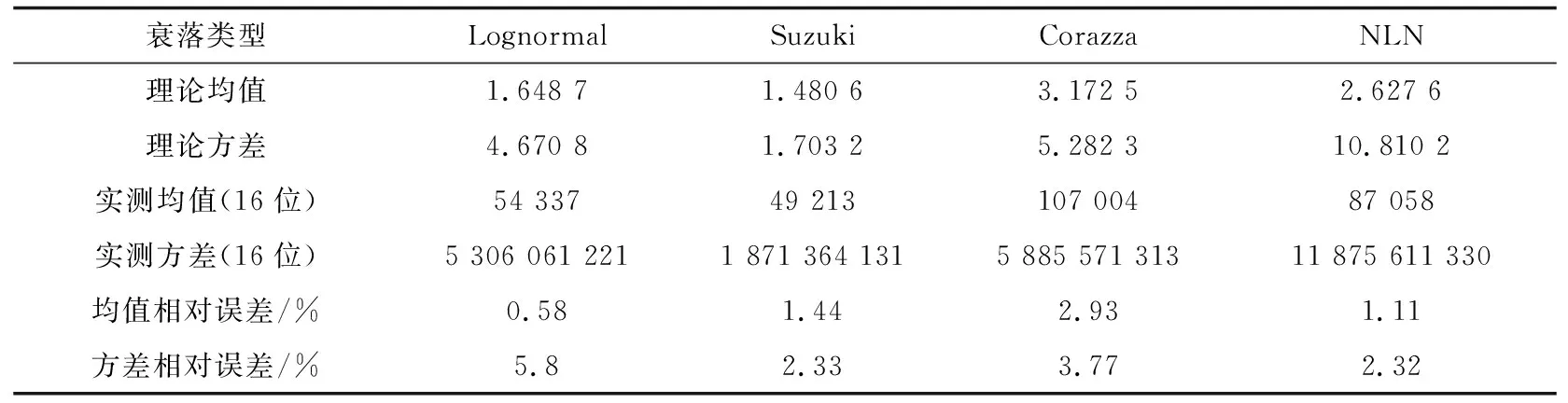
表2 输出衰落分布的均值和方差比较

4 结 论

全阴影卫星衰落信道的硬件模拟传统方法存在硬件资源消耗大与实时性差的问题，本文基于调频谐波叠加结构，提出了一种基于迭代算法与CORDIC算法相结合的卫星信道高效孪生方案。同时，结合时分复用思想，大大减少了硬件资源消耗的同时提高了系统的实时性，并支持大规模多支路卫星通信网络信道的硬件实时模拟。实测结果表明，本文算法模拟输出的信道衰落统计特性包括包络分布和多普勒频谱形状均与理论值吻合。未来将外场实测卫星数据，对本文模型参数取值进行优化校正，以更好地应用于卫星通信信道的实验室高精度硬件孪生。