一类分数阶四点边值问题正解的存在性*
潘欣媛,何小飞
(1.吉首大学数学与统计学院,湖南 吉首 416000;2.吉首大学张家界学院,湖南 张家界 427000)
1 问题的提出
近年来,分数阶微分方程边值问题引起了许多学者的关注[1-10].分数阶微分方程边值问题解的存在性的研究方法,主要有不动点理论、上下解法、单调迭代法和变分法等[3-10].Tian等[7]利用格林函数和单调迭代法研究了如下分数阶微分方程边值问题正解的存在性:

(1)

2 预备知识
定义1[1]函数y:[0,+∞)→R的α(α>0)阶Riemann-Liouville分数阶积分定义为
定义2[1]∀t>0,连续函数y:[0,+∞)→R的α(α>0)阶Caputo分数导数定义为
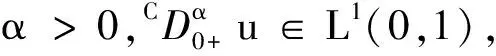
其中N是大于或等于α的最小正整数.
引理2[1]设y∈L(0,1):
(1)若ρ>σ>0,则DσIρy(t)=Iρ-σy(t),DσIσy(t)=y(t);

引理3[1](Arzela-Ascoli定理) 集合G⊂PC([0,T],Rn)相对紧当且仅当G一致有界且等度连续.
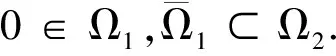
定理1若h∈C[0,1],3 (2) 证明由引理1及u(j)(0)=0,可得 (3) 由(3)式及引理2,可得 由此可知,边值问题(2)有唯一解 证毕. 定理2若h∈C[0,1],3 (4) 由此可知, 于是 证毕. 定理3函数G(t,s),H(t,s)∈C([0,1]×[0,1])有以下性质: (1)对于∀t,s∈[0,1],有G(t,s)≥g(t,s)≥0,H(t,s)≥h(t,s)≥0,其中 证明由G(t,s),H(t,s)的定义可知G(t,s),H(t,s)∈C([0,1]×[0,1]). 当0≤s≤t≤1,s≤ξ时, 那么对于∀t,s∈[0,1],有G(t,s)≥g(t,s)≥0. 当0≤s≤t≤1,s≤η时, 那么对于∀t,s∈[0,1],有H(t,s)≥h(t,s)≥0. 显然,对于∀t,s∈[0,1],有 证毕. (5) 定理4T:P→P是全连续算子. 证明对于∀u∈P,由f的定义、(5)式及定理3,有 于是T:P→P.又由f,G(t,s),H(t,s)的连续性可知T:P→P是连续的. 其中B(p,q)为Beta函数,从而T(Ω)一致有界. 当t2→t1时,|Tu(t1)-Tu(t2)|→0,即T(Ω)等度连续.由引理3可知T:P→P是全连续算子.证毕. 定理5设f∈C([0,1]×[0,+∞),[0,+∞)),存在正常数r1,r2(r1≠r2)使得以下假设成立: (H1)对于∀(t,u)∈(0,1)×[0,r1],有f(t,u)≤φp(Mr1); (H2)对于∀(t,u)∈(0,1)×[r1,r2],有f(t,u)≥φp(Nr2). 那么,边值问题(1)至少存在1个正解u,使得min{r1,r2}≤‖u‖≤max{r1,r2}. 证明由定理4可知T:P→P全连续.设Ω1={u∈P:‖u‖ 对于∀u∈∂Ω1,有0≤u(t)≤r1,t∈[0,1].由(H1),可得 于是‖Tu‖≤‖u‖. 对于∀u∈∂Ω2,有0≤u(t)≤r2,t∈[0,1].由(H2),可得 于是‖Tu‖≥‖u‖.
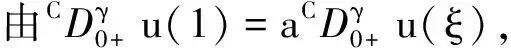


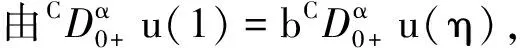
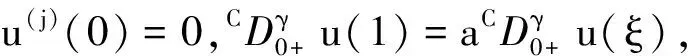

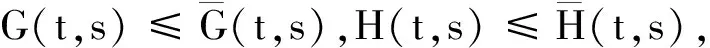
3 主要结果及其证明






