基于混合式特征选择的高分五号影像农田识别

陈珠琳，贾坤，李强子，肖晨超，魏丹丹，赵祥，魏香琴，姚云军，李娟

1.北京师范大学 地理科学学部 遥感科学国家重点实验室,北京 100875;2.北京师范大学 北京市陆表遥感数据产品工程技术研究中心,北京 100875;3.中国科学院空天信息创新研究院,北京 100101;4.自然资源部国土卫星遥感应用中心,北京 100048

1 引 言

在全球极端气候、自然灾害肆虐的环境下，粮食安全成为影响社会稳定和可持续发展的重要因素（Yu等，2019）。中国因受退耕还林还草、城市扩张等因素的影响，耕地数量逐年减少，使得粮食生产面临严峻挑战（Han 和Song，2019）。农田面积统计是作物估产的基础，因此快速、准确的农作物种植面积监测成为国家粮食宏观决策的重要支持（李强子，2018；樊东东等，2019）。

遥感技术具有动态、快速且大面积观测的特点，在农田识别中发挥着重要作用（Liu 等，2011；Xu等，2019）。目前，各类遥感数据已广泛应用于农田分类研究（Yin 等，2018；Hao 等，2019）。例如，Kussul 等（2017）基于Landsat 8 和Sentinel-1A 遥感数据，使用卷积神经网络算法实现了土地利用类型分类，其中农田识别精度高于90%。 Ghorbanian 等（2020） 基 于Google Earth Engine（GEE）平台实现了伊朗地区10 m 空间分辨率的农田识别研究，生产精度和用户精度分别为91%和90.2%。尽管如此，多光谱遥感影像的波段较少，无法避免地物间“异物同谱”的现象，从而影响了农田识别精度。相比之下，高光谱遥感数据可提供可见光到短波红外范围内的上百个窄波段信息，有潜力提高相似地物的分类精度，在农田识别方面有着巨大的研究价值（贾坤和李强子，2013；Yuan等，2020）。目前，高光谱遥感也越来越多的应用于农业遥感分类，例如，Aneece 和Thenkabail（2018） 利用EO-1 Hyperion高光谱数据，基于GEE 平台实现了5 种主要作物（玉米、大豆、冬小麦、水稻和棉花）的分类，各类型识别精度到达75%—95%。刘晓双等（2018）使用河南省平镇地区的Hyperion 高光谱数据，提出了一种结合光谱、纹理和空间信息的多特征地类提取方法，该方法将农田分类精度提高到了90%。

虽然高光谱数据可以获取更详细的地物波谱特征，但连续波段间的高相关性造成了不可避免的维数灾难。所以，在构建分类模型之前需要对数据进行降维处理，从而降低模型的复杂度，提高计算效率，并减小过拟合的风险（Ding 等，2020）。降维方法通常分为两类，一类是特征提取FE（Feature Extraction），即将原始数据进行空间变化，使生成的低维数据包含大多数原始信息，比如主成分分析法（Alvarez-Meza 等，2017）。但该类算法所得到的变量解释性较差，并且筛选结果仍需要所有变量参与运算。第二类称为特征选择FS（Feature Selection），即在原始数据中按照某种原则选取最具代表性的变量（Sylvester 等，2018），该类方法保留了数据的原始特性，使变量更具解释性。

从选择策略的角度，FS 算法可分为过滤法（Filter）、包装法（Wrapper）和嵌入式法（Embedded）（Li 等，2017）。其中，过滤法仅依赖于数据的特征来评估其重要性，尽管更加高效，但最终结果不一定对目标是最优的（Sánchez-Maroño 等，2007）。包装法依赖于学习算法的预测性，能评估所选特征的质量，虽然精度高，但效率低，不适合处理高维数据（González 等，2019）。嵌入式法是过滤法和包装法的一种权衡，它将特征选择嵌入到了模型学习中，包含了与学习算法的交互，又比包装法更有效。因此，嵌入式法也是目前研究中最常用的方法（Bolón-Canedo 和Alonso-Betanzos，2019）。然而，虽然嵌入式方法依据某种特定的算法对变量的重要性进行排序，但是这种排序并不能代表目标的最优特征子集。另外，由于嵌入式法基于特定的分类算法，所以大部分研究选择同时使用该特定的算法进行降维和分类处理（如同时使用随机森林算法的变量排序和分类功能）。但目前尚未有研究证明使用同种算法进行降维和分类处理为最佳选择。

针对上述问题，本研究提出了一种混合式特征选择算法，综合过滤法、包装法和嵌入式法的特点，改善特征选择和分类效果。本文对比了3种特征选择方法（随机森林，互信息和基于L1 正则化的方法）和3种分类算法（随机森林，支持向量机和K 近邻）的组合，并通过序列后向选择方法优选特征子集，确定最佳分类模型，以期为高光谱数据的农田分类研究提供参考。

2 材料与方法

2.1 研究区概况

研究区坐落于吉林省长春市（43°05′N—45°15′N；124°18′E—127°05′E）。该地区位于中国东北平原中部，地势平坦，海拔为137—160 m。气候类型属于温带季风气候，年降水量为600—700 mm，水热条件适合农作物生长。该地区的主要农作物为玉米，根据GF-5 影像（图1）以及同期Google Earth 高清图像，将研究区分为5 种类别：农田、森林、裸土、水体和不透水面。本研究采用目视解译选取样本点，其中农田、森林、裸土和不透水面各选取了4000 个像元，水体选择了1500个像元。在总样本中随机选取2/3的样本点作为训练数据，剩余样本则为验证数据，其中各类型样本点的个数如表1所示。

表1 训练集和验证集中样本的类型及个数Table 1 Sample type and sample number in training dataset and validation dataset/个

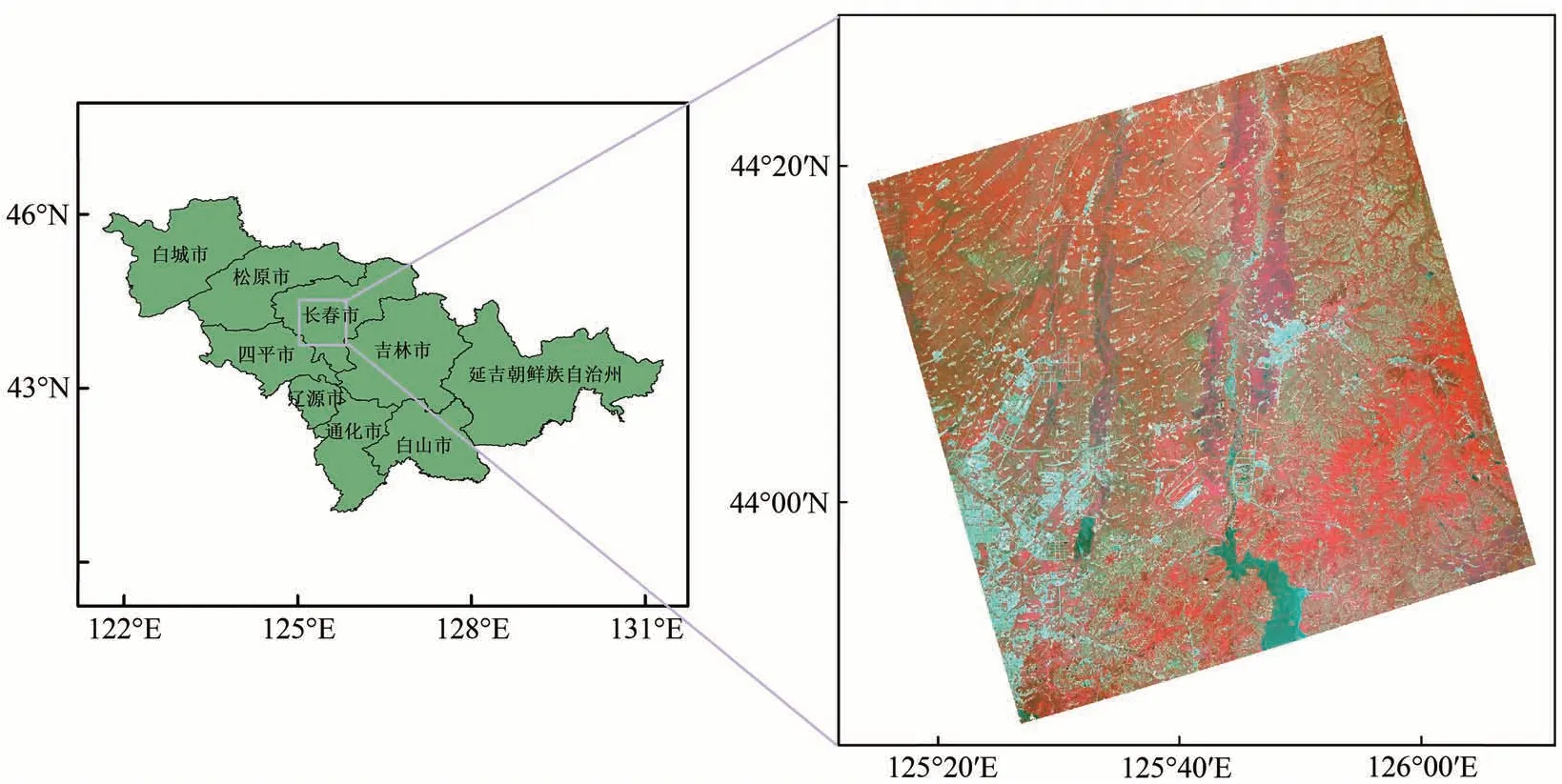
图1 研究区地理位置及高分五号伪彩色合成影像图（R：Band 107（843.768 nm）；G：Band 65（664.115 nm）；B：Band 41（561.461 nm））Fig.1 Location of study area and false color image of GF-5 hyperspectral data（R：Band 107（843.768 nm）；G：Band 65（664.115 nm）；B：Band 41（561.461 nm）

2.2 高光谱数据及预处理

GF-5 卫星是中国高分重大专项中唯一一颗高光谱卫星，其空间分辨率为30 m，幅宽为60 km，共有330 个波段（400—2500 nm），其中可见光和短波红外部分的光谱分辨率分别为5 nm 和10 nm（董新丰等，2020）。与Hyperion（224 个波段，光谱分辨率为10 nm）相比，GF-5高光谱数据不仅提供了更详细的谱段信息，同时具有更高的信噪比（刘银年等，2020）。本研究获取的GF-5高光谱数据成像于2019年7月4日，覆盖面积为3760 km2。数据获取后，首先根据同一区域的Sentinel-2 影像对其进行几何校正，然后根据每个波段的辐射定标系数进行辐射定标，最后进行FLAASH 大气校正，得到地表反射率数据。由于影像存在无效波段，经剔除后共保留295个有效波段。

2.3 研究方法

图2为本研究技术路线图。首先，对高光谱数据进行预处理，得到地表反射率数据，然后采用目视解译法选择训练和验证样本。结合不同的分类算法，分别使用随机森林RF（Random Forest）、互信息MI（Multi-Information）和基于L1 正则化（L1 regularization）的方法进行第一次降维，得到3 个特征子集。然后，再结合分类算法与序列后向选择法SBS（Sequential Backward Selection）进行第二次降维，得到9种分类模型，通过比较其验证集的分类精度，优选出最佳分类模型。

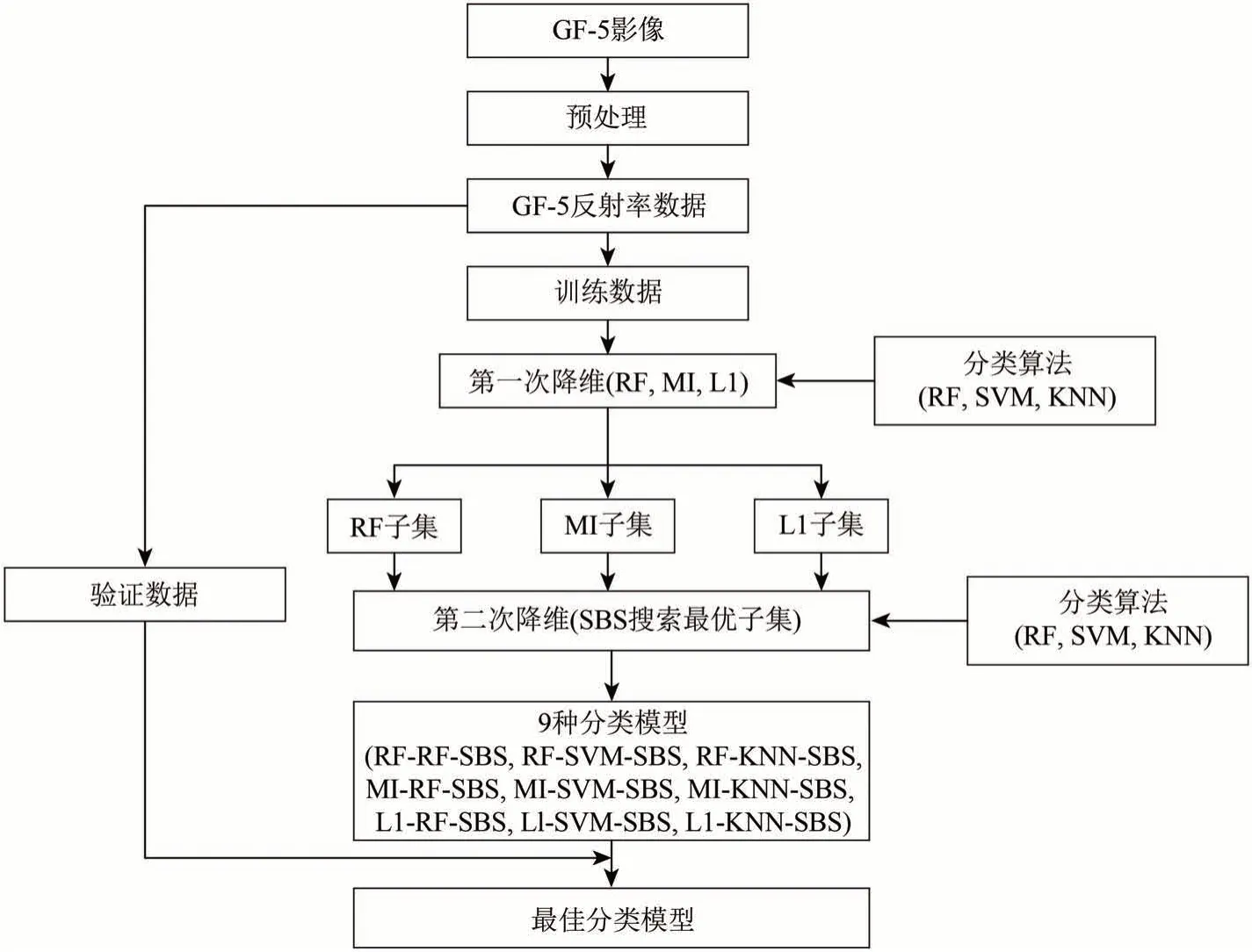
图2 本研究技术路线图Fig.2 Flow chart of this study

2.4 混合式特征选择算法

本文提出的混合式特征选择方法结合两类算法，既弥补了过滤法或嵌入式算法无法搜索最优解的缺陷，又解决了包装法处理高维数据时表现出的低效率特征。该算法首先使用具有特征排序功能或约束功能的算法（过滤法或嵌入式法），得到变量的重要性排序或约束后的特征子集。然后从特征全集开始，并按照一定的步长减小特征个数（即去除相关性较小的变量），绘制分类精度变化曲线。寻找该曲线中分类精度急剧降低的突变点，将该点所对应的特征作为特征子集。最后，使用后向序列选择算法搜索最佳特征子集，得到最终分类结果。

在混合式特征选择算法中，特征排序以及使用的分类方法是影响分类精度的两大因素。因此本研究讨论了3种具有排序或约束功能的特征选择方法和3种分类算法。

2.4.1 特征选择方法

本研究选择随机森林、互信息和L1 正则化方法对原始数据进行降维处理。其中互信息法是一种过滤式特征选择算法，随机森林和L1 正则化法均属于嵌入式算法，但二者所基于的原理不同（随机森林根据每个特征变化后对结果的影响程度判断其重要性；而L1 正则化方法则通过向成本函数中添加L1 范数，将系数矩阵稀疏化，从而达到降维目的），因此，3 种不同原理的算法被选用比较特征选择的效果。

（1）随机森林。随机森林是一种基于集成思想的机器学习算法，集成了多棵决策树的分类结果，具有精度高、稳定性强、不受高维空间影响的特点，被广泛应用于分类问题（Htitiou 等，2019；Yoo 等，2019）。在随机森林算法中，每棵决策树的袋外数据OOB（Out Of Bag）可以计算得到一个误差率，用来评价预测因子的重要性，具体步骤如下（Liu 和Sun，2019；Wang 等，2019）：首先，选择相应的袋外数据，计算每棵决策树的袋外数据误差errOOB1；其次，随机对袋外数据所有的样本特征X加入噪声进行干扰，再次计算袋外数据误差，记为errOOB2；最后，若随机森林中共有N棵决策树，则特征X的重要性值为：

（2）互信息法。互信息法属于一种过滤算法，此类算法独立于任何模型，仅依赖于数据的统计学特征来评估变量的重要性，主要包括两步（Li等，2019；Radley 等，2020）：首先，根据特征评价标准对重要性进行排序，然后选择合适的阈值或者变量个数，剔除低阶特征。互信息是一种信息度量，代表了一个变量中包含另一个变量的信息量，用于判断变量之间的相关性。假设两个随机变量X和Y的联合分布为p(x，y)，边缘分布分别为p(x) 和p(y)，则互信息I(X，Y) 是联合分布p(x，y)与边缘分布p(x)、p(y)的相对熵：

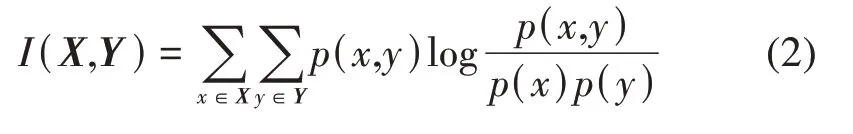
（3）L1 正则化法。高维输入不仅增加了模型的复杂度和不稳定程度，也增加了过拟合的风险。而正则化作为一种回归形式，通过约束模型的权重来产生稀疏权值矩阵，降低多项式的阶数，最终模型中系数不为0的变量则为重要变量。对于给定数据集D={(x1，y1)，(x2，y2)，…，(xm，ym)}，基于L1 正则化的嵌入式特征选择模型可以表示为（Park和Hastie，2007；Zhou等，2017）：

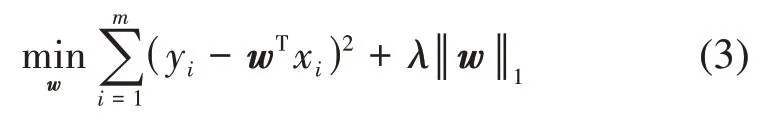
式中，w为线性拟合的系数向量，λ为正则化参数，‖w‖1为系数向量的一阶范数。

本研究使用线性SVM 作为基础模型，通过添加L1 惩罚项进行特征选择，其中惩罚系数C的搜索范围为［0.01，0.1］，步长为0.01。

（4）序列后向选择法。序列后向选择法是一种贪心算法，属于包装式特征选择法。该算法首先需要确定分类算法，然后从总特征（个数为n）开始，遍历所有n-1个特征组合，选择分类精度最高的组合进行下一步遍历，直到将变量个数缩减到最小（即n=1）。最后对比每次遍历得到的结果，找到分类精度最高的组合，即得到最佳特征子集。当面对高维数据时，序列后向选择算法的运算量大，因此有必要先用滤波法或嵌入法来寻找一个低维度的特征集合，然后利用序列后向选择算法得到最优特征子集。

2.4.2 分类方法

本研究选择了3 种常用的机器学习分类算法，包括随机森林分类、支持向量机分类和K 近邻分类算法。其中随机森林分类算法和支持向量机分类算法分别为两种嵌入式特征选择算法的基础模型，而K 近邻分类算法则独立于3种降维方法。本研究选择上述3种分类算法的目的是为了检验基于同种算法进行降维和分类是否为最优策略。

（1）随机森林分类算法。随机森林分类器是由多棵决策树分类器的投票结果所决定，基本流程为（董超和赵庚星，2020；刘杰 等，2020）：1）在训练样本中，通过boosttrap 方式有放回的抽取N个训练样本集；2）使用N个样本集构建N棵决策树模型，在每棵决策树中，从M个特征向量中随机选择m（m＜M）个特征用于内部节点划分，节点分裂标准采用基尼指数（Gini）；3）对N棵决策树的分类结果进行集成，采用投票的方式确定最终分类结果。在随机森林算法中，决策树的个数N以及节点分裂时输入的特征个数m影响着模型的分类精度和运算速度。本研究使用网络搜索交叉验证进行参数寻优，最终N和m取值分别为300和0.75。

（2）支持向量机分类算法。支持向量机是由Vapnik 提出的一种基于核的机器学习模型，由于其严格的数学理论支持、良好的泛化以及最优数值求解能力，在遥感分类领域具有广泛的应用（Maldonado 和López，2018；魏友华 等，2020）。支持向量机直接从训练数据中确定决策函数，用于寻找一个超平面对样本进行分割。在非线性情况下，支持向量机通过核函数将样本映射到高维空间，构建一个最优分类超平面，最终转化为一个凸二次规划问题进行求解。支持向量机可以在高维小样本情况下凸显其卓越的泛化能力，得到高精度的分类结果（Sukawattanavijit 等，2017；Yan 和Jia，2018）。支持向量机的核函数选用径向基核函数，其中的参数gamma 和C 使用网络搜索交叉验证进行参数寻优。

（3）K 近邻分类算法。K 近邻是一种经典的机器学习分类方法。该算法简单高效，分类性能显著，常用于数据挖掘和统计学领域（Zhang，2020）。与其他监督分类算法不同，K 近邻法不需要样本进行训练，通过将已知类别的样本作为参照，根据未知样本与所有已知样本之间的距离对其进行归类。具体流程如下：首先，对数据进行归一化处理，计算未知样本与所有已知样本之间的距离或相似度，找到与未知样本最近的K个已知样本；其次，根据已知样本所属的类别判断未知样本的归属，若K个已知样本均属于类别A，则未知样本也将被归为A类；若K个已知样本不属于同一类别，则根据少数服从多数的原则，将未知样本归为占比例最高的类别。该算法关键参数K采用网络搜索交叉验证进行参数寻优，搜索空间设置为［2，20］。

2.5 精度验证方法

本研究使用总体分类精度和召回率进行分类精度验证与评价。总体分类精度表示所有正确预测样本占总样本的比重，召回率代表某一类别里，所有样本中被正确预测的比重。其中总体分类精度作为降维的评价标准，总体分类精度和召回率作为农田分类模型的评价标准。

3 结果与分析

3.1 不同模型随维度降低的总体分类精度变化

在3种特征选择算法中，随机森林和互信息法可以得到所有变量的重要性值，并以此作为基准对变量进行排序。所以，对于随机森林和互信息法，本研究采用维度逐步递减的方式，以10 维为步长，分析不同分类算法处理下总体分类精度的变化趋势，并确定特征子集（图3和图4）。而基于L1 正则化的特征选择方法通过定义惩罚系数C 的大小得到筛选结果，变量的个数并不固定。所以本研究根据惩罚系数C的搜索范围与步长分析其总体分类精度变化趋势，从而确定特征子集（图5）。

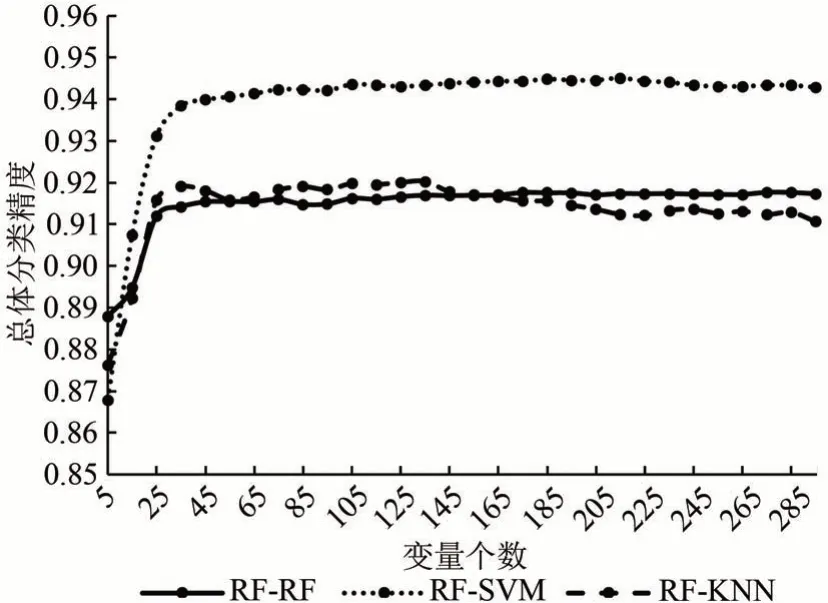
图3 随机森林排序下的不同模型的总体分类精度变化趋势Fig.3 Trend of overall accuracy of different models under random forest sorting

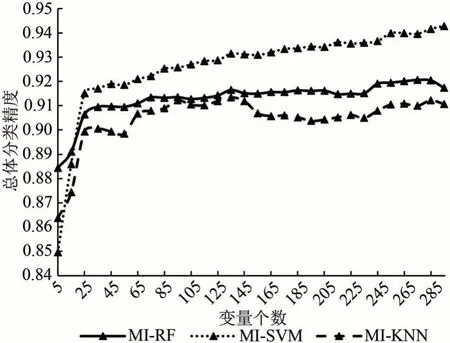
图4 互信息排序下的不同模型的总体分类精度变化趋势Fig.4 Trend of overall accuracy of different models under multi-information sorting

图5 L1正则化约束条件下的不同模型的总体分类精度随惩罚系数的变化趋势Fig.5 Trend of overall accuracy of different models under L1 regularization sorting

在随机森林特征重要性排序（图3）中，变量超过15 维的情形下，RF-SVM 模型得到的分类精度始终保持最高，而RF-RF 和RF-KNN 表现出较为复杂的现象：（1）当输入变量的维度大于155维时，RF-RF的总体分类精度大于RF-KNN；（2）而当维度低于155 维但高于15 维时，则出现相反的趋势。当输入变量个数仅为5 维时，RF-RF 在3 种模型中表现出最高的精度，而RF-SVM 则表现出较低的精度。根据上述精度变化可以得出，RF 的泛化能力较强，在较少的输入变量条件下仍可以保持较高的分类精度，而SVM 在处理高维数据时更有优势。当变量个数大于35 维时，KNN 的分类精度随维度的降低出现升高，则说明该算法对冗余数据的鲁棒性较差。

根据图3 表现的整体趋势可以看出，维度在295—25 的区间内，3 种分类方法的总体分类精度变化较小；当变量个数小于25 维时，总体分类精度出现大幅度的降低。所以，本研究将随机森林排序中重要性排名为前25 的变量作为特征子集。

在互信息排序（图4）中，变量维度从295 降低到5 的过程中，MI-RF、MI-KNN 和MI-SVM 模型的总分类精度分别降低了3.29%，4.68% 和9.32%。当变量维度大于25 时，MI-SVM 的精度均高于MI-RF 和MI-KNN，而随着维度持续降低，MI-SVM 的总体分类精度出现大幅度下降。当输入变量个数为5 维时，MI-SVM 得到的总体分类精度低于MI-RF 和MI-KNN。相比之下，MI-RF 的总体分类精度变化最小，并且在输入变量个数较少的情况下仍然保持较高的精度。虽然MI-KNN 在维度降低过程中表现出的变化趋势并不稳定（先降低后升高再降低），但在维度降至25维之前，总体分类精度仅降低1%，说明其变化幅度较小。因此，本研究将互信息排序下重要性值最高的前25个变量作为MI-RF、MI-SVM 和MI-KNN 的特征子集。

在正则化约束条件（图5）中，惩罚系数的变化对总体分类精度的影响很小，每种模型的精度最大差值分别为0.30% （L1-RF），0.35% （L1-KNN）和0.27%（L1-SVM）。当惩罚系数取值为0.01 时所对应的变量个数为27，此时模型的总体分类精度分别为92.03%（L1-RF），94.54%（L1-SVM）和92.70%（L1-KNN）。与降维前得到的结果相比，精度分别提高了0.30%，0.25%和1.64%。因此，本研究将惩罚系数取值为0.01 时得到的特征变量作为特征子集。

3.2 不同模型的特征子集及其自相关性

表2为降维前以及第一次降维处理后不同模型所对应的总体分类精度。从中可以看出，使用L1正则化方法处理后的模型（L1-RF、L1-SVM 和L1-KNN），分类精度均有提高，而MI 在降维后的模型精度均出现下降。RF 仅在使用KNN 分类模型支持下精度有所提高（提高0.52%）。分类精度提高的模型分别为RF-KNN、L1-RF、L1-SVM 和L1-KNN，其中L1-KNN 模型精度提升最大，为1.64%，而L1-SVM 模型的精度提升最小，为0.25%。尽管如此，L1-SVM 模型总分类精度仍然是所有模型中最高的，达到94.54%。

表2 降维前及第1次降维后各模型的总体分类精度比较Table 2 Comparison of overall accuracy of each model before and after the first feature selection process

为了分析不同特征选择方法造成的精度变化差异，本研究对3个特征子集的自相关性进行了分析（图6）。从图6 可以看出，MI 特征子集中包含的大部分变量集中在蓝波段和短波红外区间的连续波段，其极高的自相关性对分类精度产生了影响。因此，过滤法并不适合高维且自相关性很强的数据集。相比之下，RF 和L1特征子集中的变量不仅具有较强的代表性，而且变量波谱分布范围较为广泛。

图6 RF、MI和L1特征子集的自相关性Fig.6 Autocorrelation of RF，MI and L1 feature subsets

RF 和L1 两种方法获得的特征子集在分类过程中仍然具有明显的分类效果差异。使用RF 特征子集时，仅RF-KNN 模型的分类精度得到了提高，而L1 特征子集更具代表性，3 种模型均有不同程度的精度提升。这是由于L1 正则化在模型中添加惩罚项的方式防止出现过拟合现象，过滤了影响模型整体精度的特征。RF 通过比较每个特征变化后对结果的影响程度得到其重要性值及排序。但使用重要性值较大的变量所组成的集合进行分类，并未从整体的角度考虑到变量之间的互补或互斥特性，因此得到的分类精度低于L1正则化。

根据图6 波段分布可以发现，RF 和L1 子集中分别有11 和10 个波段分布在短波红外。不同的是，RF 子集中剩余的波段大部分集中在蓝波段和红波段，红边波段和近红外波段均仅有一个变量。而L1子集中，分别有7个和8个变量分布在红边和近红外波段，蓝波段中有2个变量，而红波段无分布。为讨论两种子集的分类精度差异，本研究对基于L1 和RF 子集模型的分类结果进行了分析（表3）。在使用RF、SVM 和KNN 分类算法的情况下，L1子集对农田的召回率较RF 子集分别提高了1.63%，3.45%和1.73%。该结果表明，与RF 子集中的蓝波段和红波段相比，L1 子集中的红边和近红外波段更有利于提高模型对农田的识别能力。

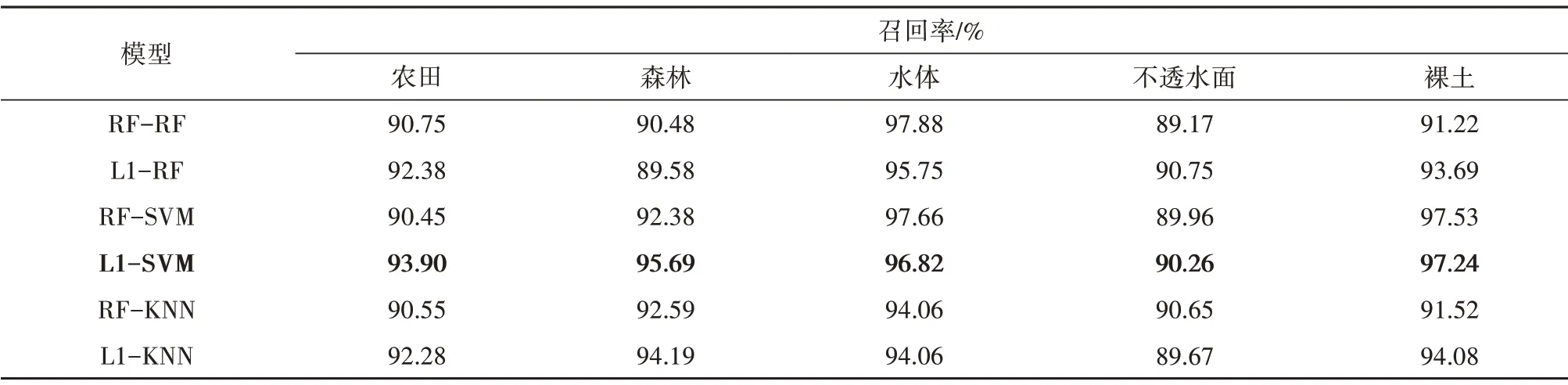
表3 基于RF和L1特征子集的分类模型对不同地物类型的召回率Table 3 Recall rate of classification model based on RF and L1 feature subset for different feature types

3.3 基于后向序列选择的降维结果及分析

在后向序列选择方法搜索最佳特征子集后，各模型的总体分类精度均有不同程度的提升（表4）。其中精度提升最大的为MI-KNN-SBS 模型（提高1.64%），精度提升最小的为L1-SVM-SBS模型（提高0.1%）。尽管L1-SVM-SBS 模型的精度提升最小，其总体分类精度（94.64%）仍然优于其他模型。表4也展示了使用后向序列选择处理后，各模型的农田召回率。与第一次降维后得到的农田召回率相比，混合特征选择算法提高了所有模型的农田识别精度。除了L1-RF-SBS 模型外，其他所有模型的农田召回率均提高了1%以上，其中RF-SVMSBS 模型的农田召回率提高最明显（增加3.86%）。这说明与单一特征选择方法相比，混合式特征选择方法不仅提升了总体分类精度，还剔除了影响农田识别度的波段，有效提高了农田识别精度。在所有模型中，L1-SVM-SBS 模型的农田召回率最高（95.83%），其次是RF-SVM-SBS 模型（94.31%）。本研究提出的方法在常规特征选择处理后，又通过使用后向序列选择法再次降维，得到最佳子集。该方法既减小了模型的输入维度，又一定程度上提高了分类精度。与单一特征选择方法相比，该方法从理论上用最优方式解决降维问题，以遍历的形式，简单、迅速的给出特定模型下的最优子集。

表4 中3 种基于L1 子集的模型（L1-RF-SBS，L1-SVM-SBS，L1-KNN-SBS）也具有较高维度的输入，这说明了L1 子集中有更多的变量对模型精度提升具有贡献性。此外，基于SVM 分类算法的模型在使用SBS 方法降维后得到的精度提升均较低，同时与其他方法相比，最优子集仍保持较高的维度。这说明SVM 分类器更适用于高维空间，对具有较高自相关性的特征子集仍然保持较好的分类精度。本研究最终选择L1-SVM-SBS 模型对GF-5 高光谱数据进行分类，分类结果和验证数据的混淆矩阵分别如图7 和表5 所示。农田的召回率为95.83%，说明该模型适用于农田识别。验证数据中分别有5.02%和7.78%的裸土像元被误分为农田和不透水面，这是由于混合像元的影响，导致裸土的识别精度相对较低。

表5 基于L1-SVM-SBS模型的分类结果混淆矩阵Table 5 Confusion matrix of classification results based on L1-SVM-SBS model

图7 L1-SVM-SBS模型分类结果图Fig.7 Classification map using L1-SVM-SBS model

表4 第2次降维后各模型的总分类精度以及所对应的输入维度Table 4 Overall accuracy of each model and the corresponding input variable dimension after the second feature selection process

4 结 论

高光谱数据在地物识别方面具有独特的优势，但其丰富的波谱信息同时也为数据处理带来了挑战。本研究提出了一种混合式特征选择方法用于高光谱数据农田分类，主要研究结论如下：

（1）使用高光谱数据进行农田分类时，L1 正则化方法能够得到最优的特征选择结果，从而得到较高的分类精度。RF 和L1正则化得到的特征子集具有较强的代表性，而基于MI 方法得到的特征子集具有较高的自相关性，严重影响了分类精度。使用同种分类算法情况下，L1子集比RF 子集得到的精度更高，说明L1 子集中的红边、近红外波段比RF子集中的蓝、红波段更适用于农田分类。

（2）3 种分类算法在高分五号高光谱数据降维和农田分类中表现出明显的差异。SVM 在高维空间中更容易实现较高的分类精度，对冗余数据有较强的抗噪性。而RF 在低维空间中表现出更强的泛化能力，可以在有限的输入特征中学习到更强的数据规律。

（3）本研究提出的混合式特征选择方法有效的将嵌入式（或过滤式）和包装法的优点相结合，即借助了机器学习算法强大的泛化能力，又结合了包装法的搜索能力，通过使用较少但更具代表性的波段，实现更精确的分类。在后续的研究中，将会通过加入纹理、植被指数等特征进一步丰富原始数据特征空间，发挥该算法的优势，从而选出更有价值的信息。