顾及空间异质性的大范围地面沉降时空预测

刘青豪，刘慧敏，张永红，吴宏安，邓敏

1.中南大学 地球科学与信息物理学院,长沙 410083;2.中国测绘科学研究院,北京 100830

1 引 言

为了满足经济发展的需要，煤、石油、天然气、地下水等多种地下自然资源被不断开采，由此产生了大范围的地面沉降（张梁等，1998）。据统计，在2009年以前，全国累计发生沉降超过200 mm 的区域面积就超过了79000 km2，仅长三角地区，在2005年以前因地面沉降造成的经济损失就已超过3000亿元（周飞飞，2012）。为了减少地面沉降的发生，营造一个安全的生活环境，地面沉降防治工作刻不容缓。

自20 世纪80年代以来，各地政府采取了多项措施来降低地面沉降的潜在危害，虽然部分城市的地面沉降问题得到了有效缓解，然而，仅通过机械地“限采”、“封井”、“回灌”等措施并不能从根本上消除地面沉降与资源开采之间的矛盾，反而造成了人力、物力、财力的被动式投入（李丽，2014）。为了避免地面沉降防治工作中社会资源的浪费，实现自然资源的可持续开发，有必要提前掌握地面沉降的时空演化规律，进而为防灾减灾、空间规划、资源开采等工作提供及时有效的指导（朱菊艳，2014），因此，开展高精度的地面沉降预测工作势在必行。

目前，大多数地面沉降预测方法都依赖于传统测绘手段（如水准测量、GPS测量等）获取的现场数据，尽管相关技术具有较高的观测精度，然而，这些数据也具有某些缺陷，例如空间代表性低、获取成本高、观测周期长等，这严重限制了开展大区域、高精度的沉降预测（朱建军等，2017）。随着InSAR 技术的发展，连续的大面积对地观测已经成为现实（廖明生和林珲，2003；张永红等，2018），在这种背景下，利用InSAR 数据和深度学习技术实现大范围地面沉降的高精度预测成为一个重要的研究方向。

实际上，现有的地面沉降预测方法可以被分为3类：数理统计方法、物理机制方法和机器学习方法。数理统计方法旨在构造明确的数学表达式来拟合沉降变化曲线。通常将地面沉降构建为关于时间/空间/时空的经验函数，李丽（2014）、范泽琳和张永红（2019）已经综述了一些经典的数理统计方法。该类方法简单易行，然而，由于未考虑地层岩性与水文介质之间的影响机制，这些方法通常仅适用于形变趋势较为简单的情况。随着研究范围的扩大，空间统计特性逐渐受到了学者们的关注，时空自回归差分移动平均（STARIMA），时空地理加权回归（GTWR）以及空间面板数据模型（SPDM）等方法也得到了广泛的应用（李世鹏，2014；Murakami 等，2006；Ali等，2020；Pesaran，2015）。区别于数理统计方法，物理机制方法需要满足复杂的固结理论假设条件，通过实测的物理参数来模拟地面沉降的物理演化过程，该类研究主要集中于地下资源开采或浅层空间开发所引起的沉降（王正帅和邓喀中，2011；张子文，2017）。然而，尽管它们可以解释地面沉降的演化过程，但是过多的参数设置及模型假设限制了该类方法的实用性。机器学习方法是通过构建特征工程、模型训练、回归预测等过程来学习沉降模式并拟合沉降，通常，他们不需要在自变量和因变量之间建立可解释的数学公式，并且免受研究区域复杂物理参数的约束。支持向量回归、人工神经网络、贝叶斯网络以及循环神经网络等方法在沉降预测领域均受到了认可（Shahin 等2003；Cao 等，2012；Ocak 和Seker，2013；Zhou 等，2019）。然而，由于特征提取困难以及样本数据粒度不同，现有的机器学习方法仍然难以得到较高的预测精度。此外，为全局所训练的机器学习模型忽略了自变量与因变量间关系会随着空间位置发生变化的事实，这导致预测结果缺乏可解释性成为了普遍问题。

综合研究背景及现状，虽然在地面沉降预测领域发展了许多研究成果，但是，已有的尝试大多是为解决小区域或独立观测站所反映的地面沉降问题。一方面，智慧城市的建设对大区域地面沉降的精准防治提出了更高要求；另一方面，基于线性假设的数理统计方法本质上难以准确模拟地面沉降的复杂非线性过程，物理机制方法因模型参数或相关数据不易获取也难以在大区域得到应用。相比来说，机器学习方法可以建模复杂的非线性时序关系，通常具有更好的预测效果，然而，该类方法并没有很好地处理空间异质现象，这导致预测误差存在空间自相关问题，因此，有必要考虑更合理的策略来预测沉降。

本文从数据驱动的角度出发，提出一种顾及空间异质性的InSAR 地面沉降时空预测方法，着重对空间异质性以及时间非线性进行研究，并利用真实沉降数据分析了模型参数对预测效果的影响，以期为大范围地面沉降提供时空预测新思路。

2 研究思路及方法

作为一种新的机器学习分支，深度学习是目前国内外人工智能领域的重点研究内容之一（Deng 等，2009；Zhou 等，2013；Sun 等，2014）。其中，循环神经网络在对序列的非线性特征进行学习时具有一定优势，已经在沉降预测领域得到了应用（Zhou 等，2019；刘青豪 等，2021）。然而，当涉及到大区域时，复杂多样的驱动因素导致沉降观测结果出现结构性异质（空间分异）以及局域异质（空间自相关）现象。如果忽略这种空间异质特征，构建的预测模型在局部区域可能会缺乏解释能力。针对这一问题，本文首先采取空间分区与局域建模相结合的策略来弱化空间异质性的影响，进而，利用循环神经网络在时间序列建模方面的优势，提出一种顾及空间异质性的InSAR地面沉降时空预测方法。

2.1 空间异质性建模

聚类分析可以根据时间序列之间的相似性和分离度将数据集划分为不同的簇，进而描述相似的特征映射，因此可用于确定空间分区（邓敏，2011）。在这项研究中，基于K-means（Wu 等，2008）和Delaunay边长约束（Estivill-Castro和Lee，2002）的组合策略（以下简称KDP）被用来处理空间分异问题。该方法不仅考虑点目标与子区中心的专题属性距离，同时保证了子区的空间独立性，因而能够得到合理的分区结果。实际上，相关关系的变异不存在明显的空间边界，尽管空间分区可以弱化全局异质性造成的影响，但是邻近点目标之间仍然存在依赖关系。为此，本文采用反距离加权的方法获取每个点目标处的时空特征矩阵，从而在训练样本中以空间特征的形式表达局域异质信息。下面具体介绍空间分区与局域建模策略。

首先，对点目标的沉降属性进行K-means 聚类。选择平均沉降速率之间的差异作为相似性度量指标，聚类结果的有效性通过经典的DB 指数（Davies 和Bouldin，1979） 和Dunn 指 数（Dunn，1974）协同确定。如式（1）—（2）所示，Si和Sj表示簇样本点到簇质心距离的均值，dij表示两簇质心间的距离，k表示簇的数量。dmin(Ci，Cj)表示两簇内任意点目标之间距离的最小值，diam(Cp)表示簇的直径。一般的，DB指数越小或者Dunn指数越大，聚类效果越好。

然后，对K-means 聚类结果中每个簇构建Delaunay 三角网并划分子区。利用边长约束参数α识别空间邻接距离较大的边，如式（3）所示，如果某边长超过所在三角网中边长均值α倍标准差，则该边被标记为弱邻接，通过删除此类长边对每个聚类簇进行二次划分，进而确定空间分区。其中，Const_Li表示簇i中构网边长约束阈值，Li表示簇i中所有边。

最后，利用反距离加权对任意点目标进行局域建模。主要步骤包括：（1）利用Delaunay三角网构建子区内点目标之间的空间邻接关系；（2）基于反距离加权分别计算0—p阶邻近处点目标产生的异质影响；（3）将局域异质信息与中心点处沉降序列融合为时空特征矩阵，作为预测模型在当前点目标处的样本源。在反距离加权过程中，权重表示为：

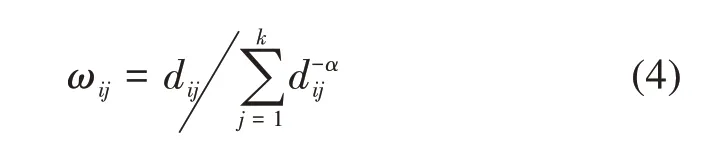
式中，ωij表示第j个点目标对第i个点目标的异质影响权重；d ij表示第i个点目标与第j个点目标之间的距离；每阶权重之和为1；幂指数α为实测值对建模位置的影响级别，α越小，权重随距离增大衰减得越慢，本文将α设置为默认值1。图1 表示局域建模示意图。

图1 局域建模示意图Fig.1 Schematic diagram of local modeling

2.2 STLSTM 预测框架

如图2 所示，STLSTM 预测框架可以分为3 层网络和3个模块：输入层、隐藏层、输出层、异质模块、训练模块和预测模块。其中，异质模块负责对时空数据进行均质化处理，隐藏层通过LSTM模型进行建模，学习每个样本中的关联信息，输出层是不同点目标预测结果的集合。STLSTM 的输入数据为经过地理编码的沉降时空序列。在异质模块，原始数据被划分为一组均质子区，每个点目标经过局域建模被处理为时空特征矩阵，局域异质信息以空间特征的形式表达在样本中。

图2 STLSTM预测框架Fig.2 STLSTM prediction framework

总体来说，STLSTM 模型的预测流程包括以下3步，首先，将标准化后的沉降数据划分为一组子区；然后，利用局域建模获取每个点目标处的时空特征矩阵；最后，构建一组LSTM 模型学习每个子区下的沉降模式。

2.3 样本划分

在本研究中，假设一些固定长度的沉降序列中包含重要的形变模式。首先，为了准确学习这些变形模式，将每个点目标对应的沉降序列标记为Sm={s1，s2，…，sm}，m表示沉降序列的总长度。其中，每个沉降时序可提取出一个长度为可控参数l的训练样本，样本的后y个值作为样本标签，前(l-y)个数值用作样本输入，且满足约束条件2 ≤l＜m、1 ≤y＜l。然后，依据局域建模的思想，将1—p阶邻近信息建模为p维空间特征并与原始沉降序列融合。最后，对每个样本进行zscore 标准化以消除沉降时序数量级对训练效果的影响，标准化后的训练样本可以表示为

式中，数据标准化的具体方法如式（6）—（8）所示，mean(Strain)和STD(Strain)分别表示任意样本序列差分沉降值的均值和标准差，st表示标准化前任意序列中某时刻的差分沉降值。

样本划分方式如图3所示。此外，样本标签长度y也可以根据预测步长进行调整。为了便于理解，图3采用单步预测方式划分样本，即样本标签长度y为1。按照这种划分方法，每个点目标可提取一个样本用于训练或测试。随机选取研究区域70%的点目标作为训练点，其余30%作为测试点，经过训练及测试调整，获取预训练的模型对未来时刻进行预测。

图3 样本划分示意图Fig.3 Schematic diagram of sample division

2.4 参数优化及模型更新

空间异质性建模和网络训练是运行STLSTM模型的主要内容。K-means 聚类可以根据沉降特征将研究区划分为若干形变区，AMOEBA 方法（Estivill-Castro 和LEE，2002）进一步将每级形变区划分为一系列均质子区，每个子区用于构建局部LSTM 模型。网络训练是一个调整权重和偏差的过程，直到满足用户定义的停止标准。在本研究中，当训练集和测试集的“误差—迭代次数”曲线都收敛时，预训练模型被认为达到训练要求。通常，满足上述条件需迭代训练20 次，该过程主要依赖于调整网络内部神经元间的连接权重及偏置。

在训练STLSTM 模型时，l、K、S、p是最为关键的网络参数，分别代表样本序列长度、网络层数、隐藏层神经元数和局域建模阶数。一般采用网格搜索策略来优化上述模型参数。在本研究中，以降低平均预测误差作为参数优化的目标，具体表示为

式中，stepl、stepK、stepS、stepp分别表示相关参数的搜索步长。通常，网络层数和隐藏层神经元数的最大搜索范围i和Smax需要根据训练效果设定经验值。在本研究中，Adam（Kingma 和Ba，2014）优化算法被用作网络训练优化器。

在网络训练达到收敛要求后，进行网络预测。首先，从每个点目标的沉降序列中截取待预测样本Spred={sm-l+1，sm-l+2，…，sm}。模型训练和预测的准确率可以定量表达为式（11）

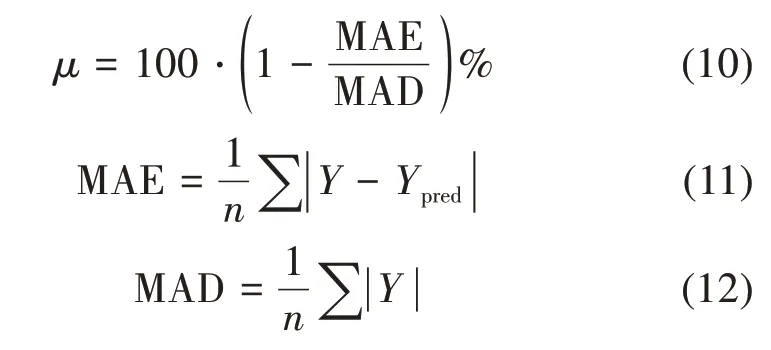
式中，μ表示模型的平均预测精度，MAE表示平均绝对误差，MAD表示平均真实形变。

总的来说，STLSTM 是一个由InSAR 数据驱动的预测器。其中，训练集和测试集仅用于训练或调整预训练模型，时间成本远低于SAR 影像更新周期（通常为12 d）。此外，预训练的模型可以预测第m时刻的沉降，当第m时刻的真实沉降数据得到更新后，预测样本Spred被立即提交给预训练的模型，从而更新模型参数。这意味着我们可以利用最新的观测结果在短时间内预测未来时刻的沉降。

3 数据概况及实验

3.1 数据概况

沧州地区是华北平原沉降最为严重的区域之一（Zhou 等，2018），该地区地面沉降具有速度快、范围广、不均匀、危害重的特点。相关研究（秦同春 等，2018；Zhou 等，2018；刘青豪 等，2021）表明，自1970年以来，该地区最大累计沉降已超过3 m，并仍处于缓慢发展阶段。为此，本研究将该地区作为研究区域，实验数据来自于Sentinel-1A 卫 星2017年1月—2019年12月采集的80 幅SAR 影像。此外，利用多主影像相干目标小基线技术（Zhang 等，2018）反演形变信息，并基于430476 个高相干点生成了累计形变时空序列（图4）。采用局部线性插值填充失相干所引起的数据缺失时段，最终，每个点目标得到89 个相等时间间隔的沉降记录。基于国家二等水准数据的精度验证结果表明，控制点与形变反演结果间的中误差为7.2 mm。

图4 沧州地区沉降空间分布Fig.4 Spatial distribution of subsidence in Cangzhou area

3.2 空间分区

为了减少空间异质性的影响，借助Matlab 2016软件环境，采用KDP 算法将研究区域划分为若干均质子区。组合策略仅需设置边长约束常数α（本文实验α=3）即可获得均质的子区。实验表明，当K-means 聚类数目为2 时（通常小于10），可以得到较小的DB 指数和较大的Dunn 指数（图5）。应该说，边长约束常数α对于最终分区数目有直接的影响，α取值越低，邻接关系的认定越严，最终的分区数目越多。

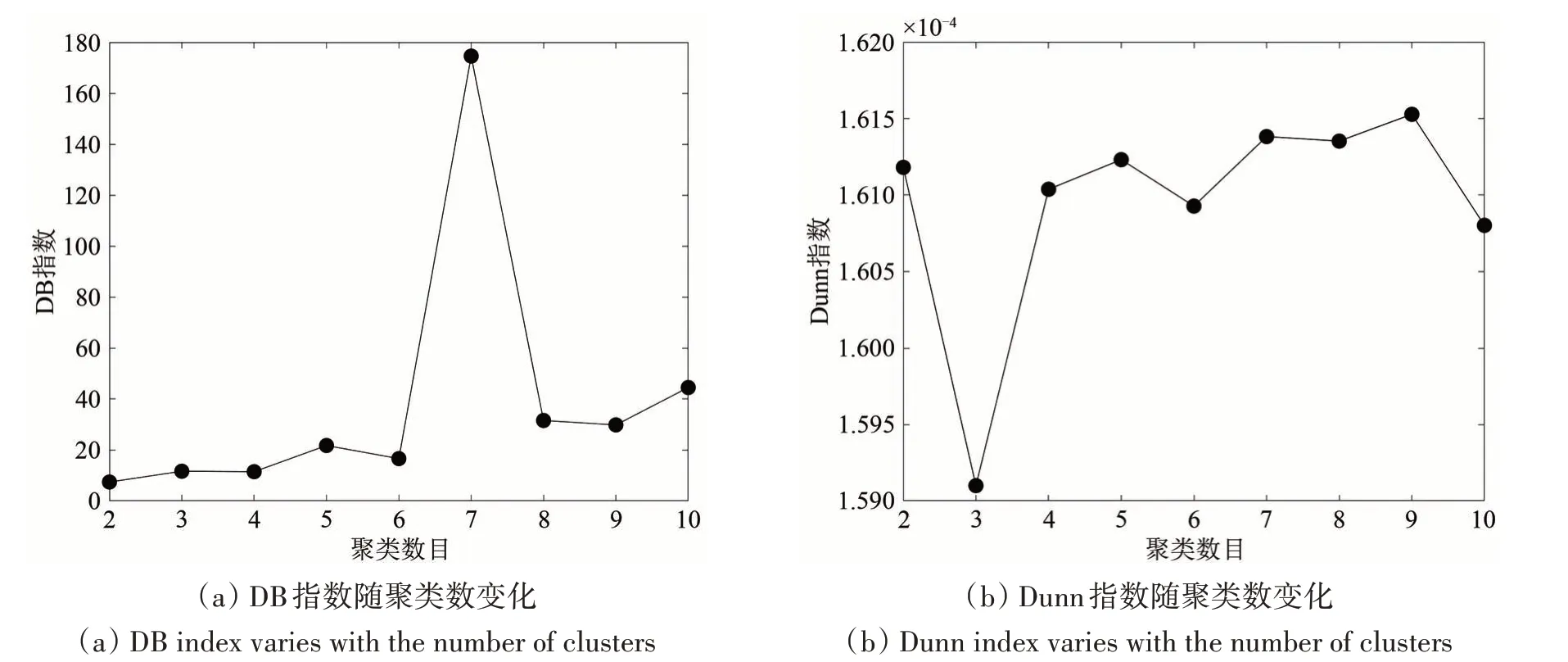
图5 不同聚类数目下的DB指数与Dunn指数分布Fig.5 Distribution of DB index and Dunn index under different number of clusters

本研究借鉴杨学习等（2016）的参数设定，进一步划分出子区2、3、5（图6）。其中，每个均质子区表示具有相似沉降特征和相邻空间位置的高相干点集合。该策略不仅描述了沉降序列间的相似性，而且与沉降漏斗的空间分布高度吻合（图6 和图4）。此外，表1 显示了基于q-统计（Wang 等，2016）的度量，结果表明，空间分区有效地削弱了研究区域的分层异质性，因此，KDP 算法可以较好地弱化地面沉降的空间异质性。

表1 分区前后分层异质性变化Table 1 Changes in hierarchical heterogeneity before and after partitioning

图6 KDP空间分区结果Fig.6 KDP space partition result

3.3 网络参数分析

首先，利用图7分析了样本标签长度对预测效果的影响。在MAE 热力图中，颜色条表示网格中MAE 取值的范围。可以发现，随着样本标签长度（SLL）的增加，不同样本输入长度（SIL）下的平均绝对误差也会提高，这条规律启发用户将SLL优先设置为1。此外，虽然误差间的差异很小，但在垂直方向上SIL 并不是一直呈现线性趋势，这表明存在一个不确定的SIL值来优化预测性能。

图7 MAE网格搜索结果（K=30，S=2）Fig.7 MAE grid search results（K=30，S=2）

然后，利用图8分析了不同网络参数下的预测效果。不同参数设置下的误差表明，模型预测精度并不总是与模型复杂度呈正相关，而是在局部形成出色的组合。当网格边界确定后，最优网络参数的分布趋于一致。例如，当“SIL=60，SLL=1”时，最优参数始终位于“网络层数为3，神经元数为10”。

图8 最优网络参数组合（SIL=60，SLL=1）Fig.8 Optimal network parameter combination（SIL=60，SLL=1）

此外，本文进一步分析了各子区不同样本输入长度下的预测结果。如图9 所示，子区1—3 被蓝色的一级形变区划分，子区4—5 被红色的二级形变区划分，黑色噪声点表示孤立点和较小簇的集合。图9 表明，当SIL 增加至一定范围后，不同子区的最小预测误差反而逐渐增加。这意味着预测效果并不总是随着SIL 的增加而改善。另一方面，虽然一些子区处于相同级别的形变区，但地理环境的差异使其产生不同的沉降模式（例如，前3个子区均由一级形变区划分得到，但是具有不同的最优SIL），这进一步说明了划分子区时需要考虑空间约束。应该说，STLSTM 的性能会受到数据量的影响，当子区点目标的数据体量较小时，训练一个拟合良好的神经网络会变得困难。在本实验中，数据体量小于1000 的子区点目标数目总占比仅为1.9%，且子区合并训练所产生的误差在大区域下并不显著（图9 中黑色折线），因此，本文将点目标数目较少的子区与孤立点合并为噪声集。

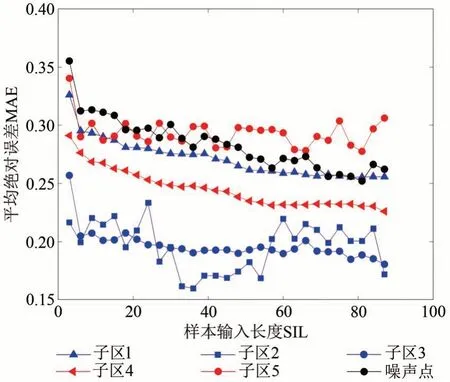
图9 不同子区SIL与MAE关系比较（p=0）Fig.9 Comparison of the relationship between SIL and MAE in different subregions（p=0）

3.4 预测方法对比

为了分析STLSTM 模型的预测性能，本文将STLSTM与二次指数平滑等其他8种方法进行比较，选取建模时间（包括预处理）和预测误差作为评价指标，所有方法使用相同的数据源。

表2 表示本文方法最终的参数优选结果。从表3可以看出，与其他算法相比，LSTM和STLSTM具有更好的性能。需要注意的是，差分自回归移动平均（ARIMA）模型和时空差分自回归移动平均（STARIMA）模型需要在每个点目标处重复建模，从而消耗大量的时间成本，因此，它们不适合应用在大区域沉降预测中。在表2中，这两种方法的建模时间为系统抽样估计值。实验结果反映：（1）在预测沉降时，为时间序列预测所设计的深度学习网络优于典型的统计方法和机器学习方法。（2）长期依赖确实对地面沉降预测有影响（比较RNN 和LSTM）。（3）新提出的空间异质性处理策略使LSTM的预测精度提高了0.6%，得到了更连续的绝对误差分布（比较STLSTM 和LSTM）。图10表明，对于相同点目标，红色预测值（STLSTM）比蓝色预测值（LSTM）更接近Y=X等值线。显然，STLSTM 对点目标预测结果的整体方法有一定的抑制作用，特别是随着真实形变量的增加，这种改进更加明显。（4）所提出的STLSTM 获得了最低的MAE和MSE，证明了所提出方法的有效性。

图10 STLSTM与LSTM方法的误差分布对比Fig.10 Comparison of error distribution between STLSTM and LSTM methods

表2 各子区的网络超参数设置Table 2 Network hyperparameter settings of each subregion

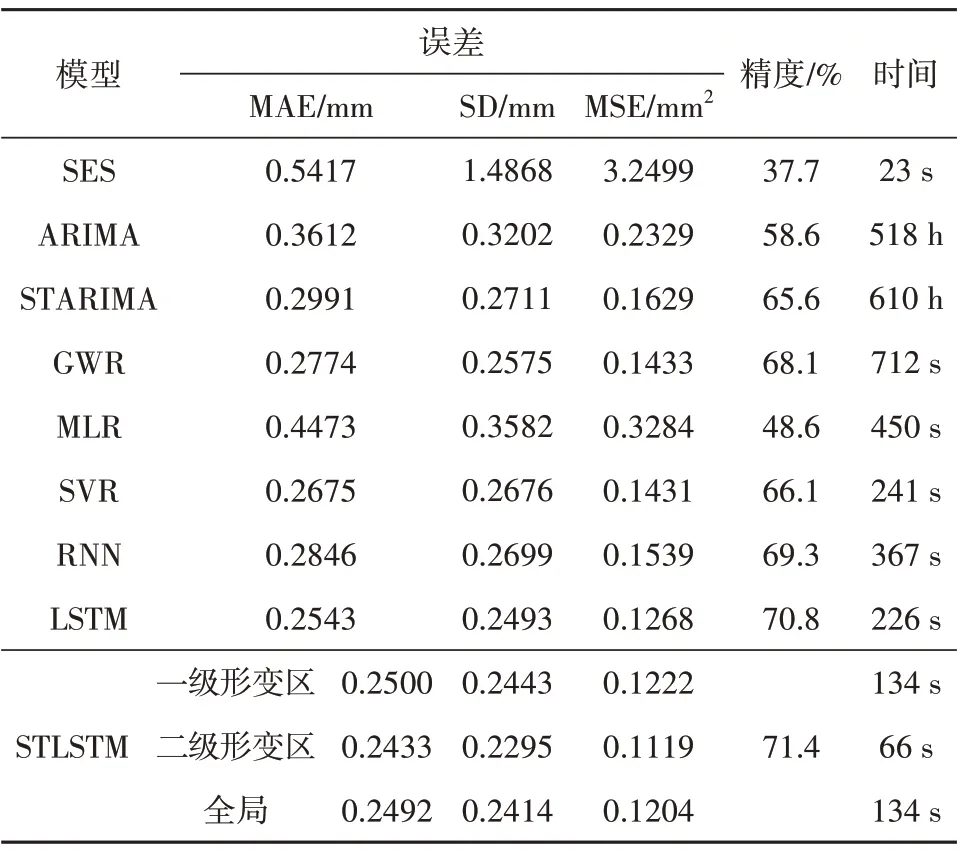
表3 不同预测方法之间的性能对比Table 3 Comparison of performance between different prediction methods

3.5 空间分析

为分析沧州地区沉降预测结果的整体效果，利用图11进行了预测值与误差值的大尺度表达。结果表明，预测值与真实沉降高度一致，沉降漏斗显示清晰，88.43%的点目标预测误差在±0.5 mm 以内。此外，在430476 个点目标中，平均预测精度达到71.4%。由于STLSTM独立训练每个子区，主要的建模时间消耗在异质模块（18 s）和子区4（134 s）。

图11 沧州地区沉降预测结果Fig.11 Prediction results of subsidence in Cangzhou area

InSAR时间序列分析为揭示地面沉降的宏观模式和演化规律提供了重要参考（朱建军等，2017）。为验证预测模型的有效性，进一步利用ArcGIS 等工具对预测结果和真实值的空间统计特征进行对比分析。如表4所示，借助不同空间分析指标对空间自相关、分层异质性、空间点格局等特性进行度量，结果表明，STLSTM 模型的预测结果并未显著改变真实沉降的空间统计特征。也就是说，大尺度的预测结果仍然保持了原始InSAR 反演结果的沉降模式，这在空间上验证了深度学习方法在沉降预测任务中的可行性。

表4 预测值与真值的空间统计特性对比Table 4 Comparison of the spatial statistical characteristics of the predicted value and the real value

4 结 论

本研究通过构建STLSTM 网络模型，将空间异质性融入地面沉降预测方法中，实现了高精度、高时效的大范围地面沉降时空预测。实验结果表明：

（1）与经典的深度学习方法（RNN 和LSTM）相比，准确性和处理时间略有提高。

（2）基于STLSTM 的沉降预测方法可以有效保持地面沉降的空间格局。通过对比预测前后的空间度量指标验证了该方法的有效性。

（3）与其他物理方法和机器学习方法相比，STLSTM 在没有水文、地质等相关资料的条件下具有更高的参考价值，然而，在实际监测应用中，仍需结合降水、开采方式等多种因素来分析地面沉降。

虽然本研究获取的预训练模型仅适用于沧州地区的时空预测任务，但STLSTM 方法对于其他区域的沉降案例同样具有可行性。需要指出的是，这项预测分析工作是由InSAR 形变数据所驱动，因此，InSAR反演过程中的一些误差源会不可避免地影响实际预测精度。此外，地面沉降的空间异质性会随时间发生变化，如何准确捕捉地理相似性是一个值得研究的问题。在进一步的工作中，将考虑更多驱动因素来实现大区域的地面沉降预测。