基于LSTM的导弹拦截点预测研究

张 露，苏 雨*，张 科，郭正玉

(1. 西北工业大学 航天学院，西安 710072； 2. 中国空空导弹研究院，河南 洛阳 471009；3. 航空制导武器航空科技重点实验室，河南 洛阳 471009)

0 引 言

近年来，随着科学技术的迅猛发展，现代战场上的战争已经变为高新技术的战争，战争模式从原来以地面机械化战争为主的模式转变成由高新技术支持的空战为主。巡航导弹因为体积小、重量轻、便于隐蔽和发射等特点在战场上得到广泛应用，其大部分飞行时间处于巡航状态，靠发动机克服前进阻力在大气层内飞行，具有突防能力强、机动性能好、命中精度高、摧毁力强等优点，能够有效地对敌方目标进行打击。但随着各类反导系统的发展，巡航导弹的生存能力受到了极大的威胁，导弹的突防打击能力面临严峻的考验，传统的导弹进攻方式难以实现现代化战争中的打击目的。因此，针对导弹突防工作进行研究已经成为当前战场上迫切需要解决的问题。

在导弹突防工作研究中，第一步就是对于拦截弹拦截点的预测，预测拦截点(Predicted Interception Point，PIP) 对于巡航导弹有效躲避拦截弹攻击、成功攻击目标地点有着重要意义，而只有准确预测了敌方的拦截点，才能确定我方利用什么方法，在何时何地进行突防并将其摧毁。

因此，国内外研究人员针对导弹拦截点预测问题开展了研究工作。目前，拦截点预测方法主要有基于弹目运动方程建立拦截几何的数值模型求解、加入导引方法利用迭代方式进行求解等。田宪科等以在空空导弹中广泛使用的破片式战斗部为例，建立了弹目相对运动模型求解拦截点，通过控制变量法，利用MATLAB进行仿真，分析了导弹拦截点的影响因素。Zarchan对于采用脉冲机动方式的导弹提出基于Lambert问题求解预测拦截点的方法。谢经纬等基于跨大气层反导拦截的背景，建立了某种拦截弹的动力学模型，对于给出的“脉冲”拦截弹模型，利用Lambert问题数值求解来获得预测拦截点，并利用拦截弹射表不断更新预测拦截点。Song等设计了一种类似于用于根部定位的Newton-Raphson方法，通过简单的迭代来实现拦截点的预测。Ann等通过轨迹优化技术获得了可实现的预测拦截点范围，并提出适当的PIP选择方案以拦截目标。但上述对于PIP的研究工作存在作战假设场景过多、适用性不强、鲁棒性较差、拦截点预测精度较低等问题。

深度学习最早可以追溯到1958年Rosenblatt提出的感知机。近些年由于计算机性能的大幅度提升，深度学习更是迎来了蓬勃的发展。深度学习具有自适应性强、鲁棒性好、容错性高、适用于非线性问题以及训练后的网络有毫秒级响应等特点。其在导弹作战领域，包括导弹参数预测、导弹发射条件优化、导弹轨迹预测等方向都有很多应用。相对于传统预测方法，基于深度学习的PIP方法更适用于现代战场高动态、强干扰的环境对导弹突防带来的挑战。因此，国内外学者开展了基于深度学习方法的导弹突防方法研究。南英等利用深度强化学习，提出一种弹道导弹突防控制方法，训练结果表明此方法能够有效地对弹道导弹终端最优突防模型进行逼近。杨子成等利用DNN网络，以拦截弹主动段关机时参数作为输入，建立预测模型，实现对拦截点和拦截时间的预测。Lee等以神经网络为基础，提出一种高速计算反弹道导弹系统的预测拦截点算法，大大减少了目标轨迹实时预测所需要的计算时间。Wang等建立了两层的深度神经网络，用于预测导弹飞行轨迹。上述基于深度学习的方法要比传统方法鲁棒性更强，限制条件较少。但从实验结果可以看出，使用简单DNN网络在面对复杂的导弹飞行时序数据时，效果并不是特别理想，且可能出现梯度爆炸或梯度消失等问题。

为了克服上述问题，本文提出了一种基于长短时记忆 (Long Short-Term Memory, LSTM)神经网络的导弹拦截点预测方法。在对导弹机动轨迹关键参数进行遍历的基础上，利用LSTM网络研究导弹机动轨迹数据中的规律性变化特点。随后，基于LSTM神经网络强大的时间序列分类与预测能力，设计智能化的方法实现对轨迹簇的分类，其更适用于时序轨迹序列，并且解决了DNN和RNN中存在的梯度爆炸问题； 利用神经网络预测方法实现对特定飞行轨迹的预测与评估，从而实现提前掌握空战战场态势变化，根据拦截弹的前一段时间运动状态来求解拦截点时刻以及拦截点位置，获得攻击主动权。

1 模型建立

1.1 导弹-目标相对运动模型

本文采用比例导引法来描述导弹-目标相对运动。比例导引法是指导导弹飞行速度矢量转动角速度和目标视线角变化率成比例的导引方法。其结合了追踪法和平行接近法的优点，也消除了这两种方法原有的一些缺点，是自动制导中目前最常用的方法。相比于其他导引方法，比例导引法可以得到较为平滑的弹道，并且导弹拥有足够的机动能力。只要参数调节合适，就可以实现对目标的准确打击。因此，使用比例导引法生成神经网络所需要的弹道库。

弹目相对运动关系示意图如图1所示。

图1 弹目相对运动关系Fig.1 Missile-target relative motion relationship

导弹-目标的相对运动关系如下：

(1)

式中：为导弹速度矢量；为目标的速度矢量；为弹目相对距离；为视线角；为比例系数，又称导航比；和分别为导弹速度向量、目标速度向量与目标线之间的夹角，亦称为前置角；和分别为导弹速度向量、目标速度向量与基准线之间的夹角。

研究中，定义拦截朝向目标方向运动为“正方向”，巡航弹飞行方向运动为“负方向”。

拦截弹的运动学模型如下：

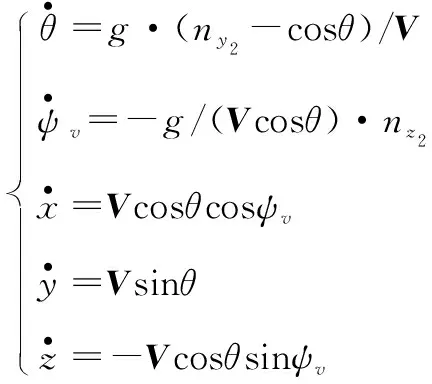
(2)

式中：为重力加速度；，，为拦截弹的三维空间位置；为弹道倾角；为弹道偏角；和分别为导弹纵向和侧向平面的过载，根据式(2)可以获得拦截巡航弹的弹道。

1.2 数据集的建立

在有监督深度学习中，最重要的部分就是数据集。因为目前对于导弹攻防对抗系统还没有公开的数据集，所以通过仿真计算多种拦截弹弹道数据，并将其作为数据集用以训练神经网络模型。

以某型号巡航导弹作为进攻弹，某型号防空导弹作为拦截弹，拦截弹发射点为原点固定点，并随机生成服从均匀分布的不同弹道倾角(∈(40°，51°))和不同发射速度下的拦截弹道。巡航导弹沿预设弹道匀速直线飞行。拦截弹每一组不同的倾角和速度初始设定值作为初始发射条件，对每条弹道分别进行攻防仿真，一共生成960条标准弹道。

拦截弹在不同速度、不同倾角情况下发射时所生成的弹道如图2所示。数据集中的全部弹道如图3所示。

图2 不同初始条件下的弹道图Fig.2 Ballistic diagram under different initial conditions

图3 基础数据集Fig.3 Basic data set

2 拦截点预测模型

2.1 模型输入参数分析

在敌我对抗双方作战流程中，拦截弹需要在导引头给出的引导信息下对姿态和发动机进行控制，从而实现对来袭导弹的精准打击。对于进攻弹来说，只要在对方拦截弹的末制导阶段，准确预测其拦截点和拦截时刻，就能提前对导弹未来弹道进行规划，从而躲避拦截弹的探测范围或机动打击范围，实现突防。

为了准确预测拦截弹的拦截时间和拦截点信息，需要进攻方探测设备对拦截弹进行准确的探测跟踪，获取拦截弹的位置、速度等信息。目前常用的导弹导引头能够获取敌方导弹的视线角、视线角速度、弹目相对距离、弹目相对速度信息，通过这些信息就可以计算出敌我对抗双方的相对位置等信息。本文利用LSTM神经网络对导弹拦截点进行预测。

2.2 LSTM神经网络结构

LSTM神经网络是一种改进的循环神经网络(Recurrent Neural Network，RNN)，最初由Hochreiter和Schemidhuber于1997年提出，主要是为了解决RNN对长序列样本训练过程中的梯度消失和梯度爆炸问题。LSTM模型是RNN模型的一个变种，主要用于解决RNN对长期依赖信息学习能力缺乏的问题。与RNN不同，LSTM在每个神经元中引入了3个“门”结构：输入门、遗忘门和输出门，通过对3个门的控制来实现对历史信息的记录，从而在更长的序列中有更好的表现。图4所示为LSTM模型的结构示意图，其中：-1和分别代表-1时刻和时刻的细胞状态；-1和分别代表-1时刻和时刻的隐藏层状态。

图4 LSTM模型结构示意图Fig.4 LSTM model structure diagram

LSTM的关键是Cell的状态。在整个网络中，各Cell之间只存在少量的线性交互过程，时序序列的历史信息在整个网络结构中传递时很容易被保存。

2.3 拦截点预测网络

所提出的拦截点预测模型如前文所述。模型输入为拦截弹3个位置参数，，的时序序列，模型的输出值为拦截点的类型，通过此输出得到拦截点的坐标(，，)和拦截时刻。设计的网络输入层节点为3，输出层节点为1，表示输出此时轨迹的类别。拦截点预测模型示意图如图5所示。

图5 拦截点预测模型示意图Fig.5 Schematic diagram of interception point prediction model

此外，为了提高网络对非线性时序序列预测问题的拟合能力，在各隐藏层后加入了激活函数，以解决线性模型中表达能力不足的问题。

常用的激活函数有sigmoid函数、线性整流函数 (Rectified Linear Unit，ReLU)、双曲正切函数(tanh) 等。相比于其他两种函数，线性整流函数更符合本文所提神经网络的需求，能够更加有效地解决梯度下降和反向传播问题，同时也避免了梯度爆炸和梯度消失问题。

本文提出了一个两层LSTM模型，网络结构如图6所示，具体参数如表1所示。

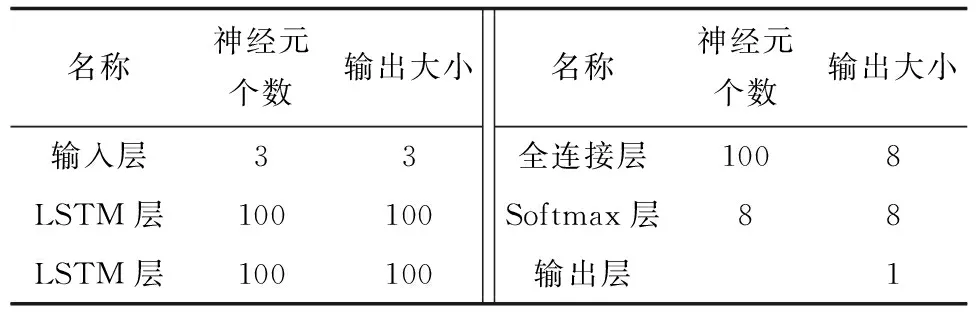
表1 拦截点预测网络结构

图6 拦截点预测网络结构Fig.6 Interception point prediction network structure

在网络结构都确定之后，需要选择恰当的损失函数和优化器对网络进行训练。损失函数表示预测值和标签值之间的误差大小，优化器是用于加速神经网络训练的加速方法。

(1) 损失函数的选择

采用交叉熵(Cross Entropy)函数作为损失函数，用来判断预测值与真实值之间的误差：

(3)

式中：()为真实分布；()为非真实分布。

(2) 优化器的选择

神经网络的基本训练方法是梯度下降法，即让损失函数按梯度搜索方法找到最小值。目前常用的方法有SGD，Adagrad，RMSProp和Adam等。本文选择SGD作为优化器，相对于其他的优化方法，该方法更适用于大数据集的训练。

3 网络的训练

3.1 数据库建立

根据前文所得到的弹道数据集，记录每条弹道轨迹的数据点，共960条弹道。在弹目相对运动刚开始时，敌我双方距离过远，我方探测器很难探测到敌方拦截弹。因此，取拦截弹的轨迹坐标从第900个点开始，第1 600个点作为结束。将轨迹的前900～1 600个点作为神经网络模型的时序输入，将拦截点坐标分为8类。对得到的样本数据进行预处理，用其中720条弹道，占总数75%的数据作为神经网络的训练集，另外240条弹道，占总数25%的数据作为测试集。

数据的预处理首先是野值剔除，即在实验之前剔除样本中某些测量的异常数据值，以减少实验成本。第二步是数据的归一化处理。本文数据集中的数据值往往都比较大，这会给计算造成较大的负担，因此，需要对目标的位置信息进行归一化处理，通过恰当的变化使得神经网络的输入、输出限制在[-1，1]之间，从而减少数据中极大值和极小值对神经网络预测的影响，同时还能够提高神经网络的运算速度。

弹道数据归一化的数学描述如下：

(4)

式中：为样本值；为样本值最小值；为样本值最大值；为归一化之后的样本值。

3.2 LSTM神经网络的训练

网络结构、训练数据、损失函数都已经设定，接下来要开始对网络进行训练。针对所提出的网络，采用以下设置进行训练：训练次数为400轮，每一轮训练迭代1次，初始学习率设置为0.1，在100轮训练之后变为0.01，最小批次为128，在单CPU上进行训练。

整个预测网络训练流程图如图7所示。

图7 训练流程示意图Fig.7 Training process diagram

4 仿真结果

4.1 实验结果

将神经网络预测输出与原测试数据集的标签进行对比，可得到拦截时间与拦截点的误差，如表2～3所示。

表2 测试集上拦截时间误差

表3 测试集上拦截点距离误差

图8～9分别为测试集中拦截时间误差分布概率和时间误差分布。从图中可以看出，测试集的时间误差分布在0.1～0.5 s，均值为0.3 s。

图8 测试集时间误差分布概率Fig.8 Distribution probability of time errors in test set

图10～11分别为测试集中拦截点距离误差分布概率和距离误差分布。从图中可以看出，拦截点距离误差分布在20～180 m，均值为102 m，距离误差在合理范围内。从结果分析可知，数据集上拦截点预测误差与拦截时间误差分布比较均匀，而且相对于弹目距离来说较小，对于后续的突防工作几乎没有影响，在精度上符合预期。

图9 测试集时间误差具体分布Fig.9 Specific distribution of time errors in test set

图10 测试集距离误差分布概率Fig.10 Distribution probability of distance errors in test set

图11 测试集距离误差具体分布Fig 11 Specific distribution of distance errors in test set

4.2 模型对比

将所提出的基于LSTM的拦截弹预测模型与其他方法进行对比，结果如表4所示。图12为3个不同网络训练过程中测试集loss的变化曲线； 图13为3个网络训练过程中测试集准确率变化曲线。从图中可以看出，DNN网络和RNN网络对本文的数据集训练结果并不理想，分类精度不够高，训练过程中loss变化趋势也比较乱，甚至出现梯度消失或梯度爆炸问题。与之相反，本文所提出的LSTM网络在处理导弹轨迹时序数据时效果很好，能够在极少的迭代次数下收敛，并且准确率和loss的变化趋势要更加理想。从测试集的结果可以看出，本文提出的网络结构预测精度要高，对时序序列处理效果更好。这是因为相比于DNN和RNN，LSTM有3个门(输入门、遗忘门、输出门)结构，其中遗忘门能够对历史信息进行处理、保存或者丢弃，从而能够找到数据中的时序相关信息并避免可能出现的梯度消失和梯度爆炸的问题。

表4 实验结果对比

图12 测试集loss变化对比Fig.12 Comparison of loss accuracy changes in test set

图13 测试集准确率变化对比Fig.13 Comparison of accuracy changes in test set

4.3 模型适用性分析

为进一步分析所设计的网络模型的适用性，增加了样本集以外的文本数据集进行分析。在此，使用了IMDB数据集。此数据集包含50 000条偏向明显的影评，其中25 000条作为训练集，25 000条作为测试集，标签为积极(pos)和消极(neg)两种。使用LSTM模型与两种对比算法对此数据集进行分类。

对IMDB数据集测试集分类结果如表 5所示。图14为3个不同网络训练过程中训练集准确率变化曲线； 图15为3个网络训练过程中训练集loss的变化曲线； 图16为3个不同网络测试集准确率变化曲线； 图17为3个网络测试集loss的变化曲线。从实验可以看出，DNN网络在训练时正确率和loss的变化相比于本文方法都十分理想，收敛也很快。但是在测试集上的准确率比本文模型低了近20%。很容易就能看出，DNN在处理复杂文本数据时出现了严重的过拟合现象，而LSTM则没有。RNN网络没有明显的过拟合现象，但观察训练过程，其效果没有LSTM好，而且分类精度也没有LSTM高。这是因为DNN中不存在对时序信息处理的结构，因而其效果最差。而RNN可以存储时序序列历史信息，能在一定程度上改善时序序列处理效果，但对于长时间依赖序列，其仍存在一定缺陷。LSTM提出的网络使用了LSTM网络结构，其门结构能够选择性地对数据进行处理，所以更适用于存在时间依赖性数据的处理任务。从上述分析可知，本文模型相比于其他两个网络，在文本分类数据集上也能有一定的应用。

图17 测试集loss变化对比Fig.17 Comparison of loss changes in test set

表5 测试集分类精度对比

图14 训练集准确率变化对比Fig.14 Comparison of accuracy changes in train set

图15 训练集loss变化对比Fig.15 Comparison of loss changes in train set

图16 测试集准确率变化对比Fig.16 Comparison of accuracy changes in test set

5 结 论

本文主要研究了巡航导弹突防过程中针对拦截弹的拦截时间和拦截点预测问题。相比于传统的建模方法，神经网络具有自学习与自适应性强、鲁棒性强和容错率高、适用于非线性问题等特点，而其中LSTM网络又能很好地解决神经网络中对于长时间依赖序列容易出现的梯度消失或梯度爆炸问题。因此，本文采用基于LSTM网络的有监督学习方法，实现对于拦截弹拦截点和拦截时间的预测。将本文方法与现有方法对比可以看出，本文方法更加适用于长时序序列的预测问题，且能够在更少的迭代次数下得到较高的预测精度。

从实验结果可以看出，本文所提出的拦截点预测模型，无论是从预测精度还是适用性都要优于已有的模型，能够更好地实现对拦截点和拦截时间的预测。这为后续的导弹突防工作提供了良好的理论和技术基础。