考研数学中关于“大数定律与中心极限定理”的解题研究
陈贝宁 张莹婕 曹钰涵
1.河海大学商学院 江苏常州 213022;2.河海大学里尔学院 江苏南京 201198
大数定律和中心极限定理作为概率论与数理统计知识中的重要板块,多次出现在考研数学真题中,题型较为灵活多变,如果考生只是简单地了解定理内容,而不能在解题中灵活运用,则很容易失分。因此,备战考生们应秉持着耐心的态度去认真复习这一板块。首先,需要熟悉切比雪夫不等式的内容,重点理解其应用;其次,必须把大数定律的结论理解透彻;最后,需要掌握中心极限定理的结论及其应用。
大数定律和中心极限定理作为重点内容,不仅会通过选择题或填空题的方式来呈现,还会作为知识点出现在综合题中。考点比较固定,主要考察大数定律和中心极限定理的结论如辛钦大数定律、独立同分布的中心极限定理等。
接下来通过梳理历年考研真题,探讨解题思路,归纳常见考点,有利于考生提高复习效率。
1 大数定律
人们在长期实践中发现,随机进行某种试验时,若试验次数很少,结果往往是无规律可循的,不具有确定性,但是在一定条件下,当试验次数逐渐增多,其结果往往会趋向稳定,呈现出一定的规律性,即大量重复的随机现象的总体性规律一般是以算术平均值的形式表现出来。大数定律就是由上述概率论命题衍生出的重要理论之一。
定理一(切比雪夫Chebyshew定理)[1]
若{Xn}为一列两两不相关的随机变量序列,若每个Xi的方差存在,且有共同的上界,即Var(Xi)≤c,i=1,2,…,则{Xn}服从大数定律,即对任意的ε>0,下式成立。
定理二(贝努里Bernoulli定理)[2]
设fA是n次独立重复试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意正数ε>0,有:
定理三(辛钦Kinchin定理)[2]
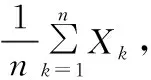
2 大数定律和中心极限定理的关系的探讨
上述简要介绍了大数定律的几个重要定理,尽管它们在表达方式上有所不同,但是它们都表达同一个原理,即在大量重复的样本条件下,样本平均值可以近似看成是总体平均值(数学期望)。而中心极限定理在大数定律的基础上进一步发展,以数量形式从随机变量的分布律方面揭示了分布律的极限问题[3],其核心思想是大量独立同分布的变量和的极限分布服从于正态分布。
大数定律重点阐述的原理是:
可见,中心极限定理和大数定律的关系是密不可分,前后衔接的。
3 中心极限定理的结论和应用
定理四(独立同分布的中心极限定理)[5]
设X1,X2,…,Xn,…独立同分布随机变量序列,且E(Xk)=μ,Var(Xk)=σ2,则对任给x∈(-∞,+∞),均有:
其中φ(x)是标准正态分布N(0,1)的分布函数。
定理五(李雅普诺夫Liapunov定理)[6]
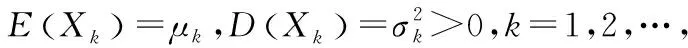
的分布函数Fn(x)对于任意x,满足:
定理六(德莫佛—拉普拉斯De Moivre-Laplace定理)[6]
设随机变量ηn(n=1,2,…)服从参数为n,p(0 中心极限定理作为概率论与数理统计的重要理论之一,描述了独立同分布随机序列的和以及算数平均的分布性质,广泛应用于实际生活,为解决实际问题提供了有力的理论支撑。下文从几个例子来具体说明其运用。 例1 一公司有50张签约保险单,各张保险单的索赔金额为Xi,i=1,2,…,50(以千美元计)服从韦布尔分布,均值E(Xi)=5,方差D(Xi)=6,求50张保险单索赔的合计金额大于300的概率(设各保险单索赔金额是相互独立的)。 则50张保险单索赔的合计金额大于300的概率为0.19%。 例2 某药厂断言,该厂生产的某种药品对于医治一种疑难血液病的治愈率为0.8,医院任意抽查100个服用此药品的病人,若其中多于75人治愈,就接受此断言,否则就拒绝此断言。若实际上此药品对这种疾病的治愈率为0.7,问接受这一断言的概率是多少? 解析:若实际上治疗率为0.7,即X∽N(100×0.7,100×0.7×0.3)。 所求概率: P1=P(X>75) =1-φ(1.09) =1-0.8621 =0.1379 例2 (2014数学一)设总体X的分布函数为: 其中θ是未知参数且大于零。X1,X2,…,Xn为来自总体X的简单随机样本。 答案:存在α=θ,使得对任意的ε>0,有: 例1 (2001数学三)一生产线生产的产品成箱包装,每箱的重量是随机的,假设每箱平均重50千克,标准差为5千克,若用最大载重量为5吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少箱,才能保障不超载的概率大于0.977(φ(2)=0.977,φ(x)是标准正态分布函数) 答案:每辆车最多可以装98箱。 解析:设Xi(i=1,2,…,n)是装运的第i箱的重量(单位:千克),n是所求箱数。由题设可以将X1,Xi,…,Xn视为独立同分布的随机变量,而n箱的总重量Sn=X1+X2+…+Xn是独立同分布随机变量之和。 由题设,有: 所以: E(Sn)=E(X1+X2+…+Xn) =E(X1)+E(X2)+…+E(Xn) =50n D(Sn)=D(X1+X2+…+Xn) =D(X1)+D(X2)+…+D(Xn) =25n 则根据列维-林德伯格中心极限定理,知Sn近似服从正态分布N(50n,25n),箱数n根据下述条件确定: =φ(2) A.1-φ(1) B.φ(1) C.1-φ(2) D.φ(2) 答案:B 即N(50,25)。 =φ(1) 大数定律和中心极限定理作为考研数学中的考查内容之一,其重要性不容忽视。考生不仅需要理解定理内容,更应在此基础上把它和其他知识点有机结合起来,灵活运用。本文详细介绍了概率论与数理统计中的重要内容——大数定律和中心极限定理,从对定理内容的逐步说明到考研真题的思路解析,深刻剖析了大数定律和中心极限定理的本质,有助于考生不再局限于课本定理内容,达到了快速抓住问题本质,选取最佳解题路径的效果。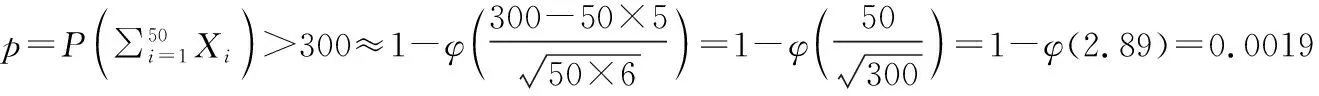
4 历年考研题中大数定律的应用

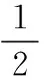
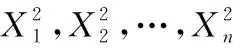

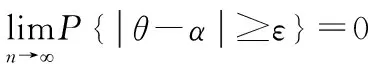
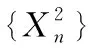
5 历年考研题中中心极限定理的应用
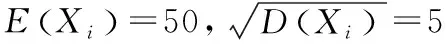


结语

