顾及约束条件的Dijkstra算法的正射影像接缝线生成与优化方法研究

李茂森

(1.核工业航测遥感中心,河北 石家庄 050000; 2.中核三维地理信息工程技术研究中心,河北 石家庄 050000)

当前,由无人机航空摄影的影像数据生产出的大比例尺数字正射影像容易获取地理信息数据,为我国的相关部门提供数据支持,特别是在城区规划、土地规划等方面发挥了巨大作用。另外,数字正射影像图可以预测我国经济社会的发展趋势,为相关部门未来几年、几十年提供规划依据[1]。无人机航空摄影获取影像数据生产数字正射影像图的关键步骤就是影像镶嵌[2],影像镶嵌技术是对有重叠区域的航空影像数据根据接缝线多边形进行拼接生成数字正射影像图。

诸多学者已对此进行了深入研究,如潘俊[3]提出了一种基于全局的接缝线自动生成方法,此方法为提高生产影像的效率进行了并行计算,但是,此方法只能在重叠区域是凸多边形的情景下使用,并且两张影像重叠多边形仅有两个交点;袁修孝等[4]在极小化极大算法改进的基础上,利用贪心式算法生产接缝线;沈佳洁等[5]提出了一种基于均值漂移分割的接缝线生成方法,该方法的优点是能够让生成的接缝线出现在最优的穿越区域中,但是该方法的局限性是在时间上相对比较耗时;袁胜古等[6]提出了一种基于自适应分水岭分割航空影像接缝线优化方法,这种方法也可以将接缝线绕开高程较大的建筑物和独立地物等,但是此方法受分割参数的影响较大。

研究在数字表面模型(DSM,digital surface model)上提取候选点构建三角网并赋权值,利用计算几何算法库(CGAL,computational geometry algorithms library)查找出搜索最短路径的起始点和终止点。然后根据影像外方位元素对Dijkstra搜索最短路径算法进行矩形搜索约束,再将搜索出的最短路径追踪出接缝线多边形,并对多边形中极大与极小多边形进行基于定位影像与影像外轮廓的优化,最后进行单张正射影像拼接,并与voronoi方法拼接的正射影像进行主观视觉与客观数据对比分析。

1 候选点Delaunary算法构网

由于DSM上地面点数量可观,所以选取哪些地面点作为候选点至关重要。在整个测区的DSM上计算每一个像素高程点在一定大小窗口内的密度,将密度大的像素点作为候选点提取出来,这样提取出的候选点是离散点,再对候选点进一步处理得到初始的接缝线线段。最后利用Delaunay算法将提取出的候选点构成三角网(见图1),并对三角网中的边赋权值。

图1 候选点构成的三角网Fig.1 Triangulation mesh of candidate points

2 顾及约束的Dijkstra搜索最短路径

2.1 Dijkstra经典算法

Dijkstra(迪杰斯特拉)算法是典型的寻找两点之间最短路径算法[7]。目前最短路径算法已有几十种,包括Bellman-Ford算法[8]、Floyd算法[9]、蚁群算法[10]、动态规划方法[11]、神经网络[12]、遗传算法[13]以及进化算法[14]等,Dijkstra以极强的抗差性能在软件应用中被广泛采用。

Dijkstra算法一般将网络定义为有向图G=(N,E),N表示网络的节点集,共有n个节点,E⊆N×N表示网络的边,共有m个边。为了描述方便,定义S表示起始点,D表示目标节点,W(i)表示从起始点S到节点i的实际距离,DR(i,j)为节点i到节点j的直线距离,C(i,j)为节点i到j的实际距离,Q表示可选的临时节点集合,P(j)表示节点j的状态。

Dijkstra算法详细步骤如下:

(1) 初始化:Seti=S,W(i)=0,W(j)=∞∨j≠i,P(i)=NULL,Q=N;

(2) 节点选择:从Q中去除W值最小的节点k,W(k)=min [W(j),j∈Q];Q(k)=permaently labeled;

(3) 节点扩展:对于和k相连的每个节点j,j∈Q,如果W(j)>W(k)+C(k,j),则W(j)←W(k)+C(k,j);Q(j)=temporarily labeled;Q←Q-{k};

(4) 停止判断:如果k=D,则算法结束;否则转第(2)步。

2.2 顾及约束条件的Dijkstra算法

Dijkstra算法需要遍历所有点来搜索起始点和终止点的接缝线最短路径,因此在解算的时间效率上比较耗时。为了提高搜索接缝线最短路径的时间效率,给起始点和终止点之间搜索最短路径增加约束条件,这种约束条件是首先计算影像每个外方位元素到其他外方位元素的距离,并计算出最小距离,将所有最近的外方位元素的距离累加求出平均值(m_eoAveragelen),再计算出起始点与终止点的最小外接矩形,并将最小外接矩形扩充m_eoAveragelen的距离,将起始点和终止点的搜索范围限制在矩形区域内,从而提高搜索的时间效率。

Dijkstra约束搜索最短路径的基本步骤如下:

步骤1查找需要搜索最短路径的起始点和终止点。利用计算几何算法库CGAL将初始接缝线构建拓扑关系,这样就形成了点线面的拓扑关系,并且拓扑关系中的边为双边结构。访问每个非边界面上的线,从拓扑关系中的一条线的起始点开始,如果这条线的起始点和终止点是两度(这个点至少被三条边共有)以上的点,并且这条线的对边所属的面不是边界面,那么这两个点就是需要Dijkstra算法查找最短路径的起始点和终止点,并将起始点和终止点连接组成线段,如图2(a)所示。

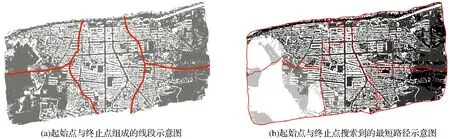
图2 Dijkstra算法搜索最短路径前后对比Fig.2 Comparison diagram of Dijkstra algorithm resolving the shortest path problem before and after

步骤2Dijkstra算法约束。首先计算航空影像每个外方位元素到其他外方位元素的距离,并计算出最小距离。将所有最近的外方位元素的距离累加求出平均值(m_eoAveragelen)。再将需要调整的起始点和终止点计算出最小外接矩形,将最小外接矩形向外扩充,扩充大小为m_eoAveragelen。扩充出的外接矩形就作为Dijkstra搜索最短路径的约束条件,继而搜索起始点和终止点的最短路径,如图2(b)所示。

3 接缝线多边形的生成与优化

3.1 生成接缝线多边形

Dijkstra算法在约束条件下搜索结果为多组线段,并非多边形,所以需要将Dijkstra算法搜索最短路径结果组成多边形。研究通过线段追踪的方法将搜索的最短路径结果组成接缝线多边形,具体操作如下:

(1) 从Dijkstra算法查找出最短路径中所有线段的一条线段开始,线段的起始点到终止点的方向定义为正方向,终止点到起始点的方向定义为负方向。

(2) 从节点出发查找线段,若这条线段的方向为正方向,找到这条线的最后一个点;若这条线的方向为负方向,找到这条线的第一个点。如果当前的节点(startLineId)连接了两条或三条线段,将当前线段的上一条线段作为新的curLineId,当前线段的上一条线段的方向作为新的方向,若startLineId等于curLineId,就停止查找,并将查找到的线段做标记,防止重复查找。再从下一个节点出发,生成新的多边形。

(3) 将面积最大的多边形删除,此面积最大的多边形是所有多边形的外轮廓。

(4) 将生成的接缝线多边形以可视化图形输出,如图3所示。

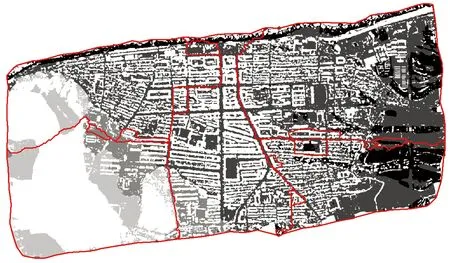
图3 接缝线多边形Fig.3 Seam line polygon

接缝线多边形的局部放大结果如图4所示。从图4中可以观察出生成的不规则接缝线多边形中形状大小各不相同,并且面积极大与极小的多边形是邻接关系。这种面积大小不同的多边形对单张正射影像的拼接会产生两种直接影响。这两种直接影响是指:

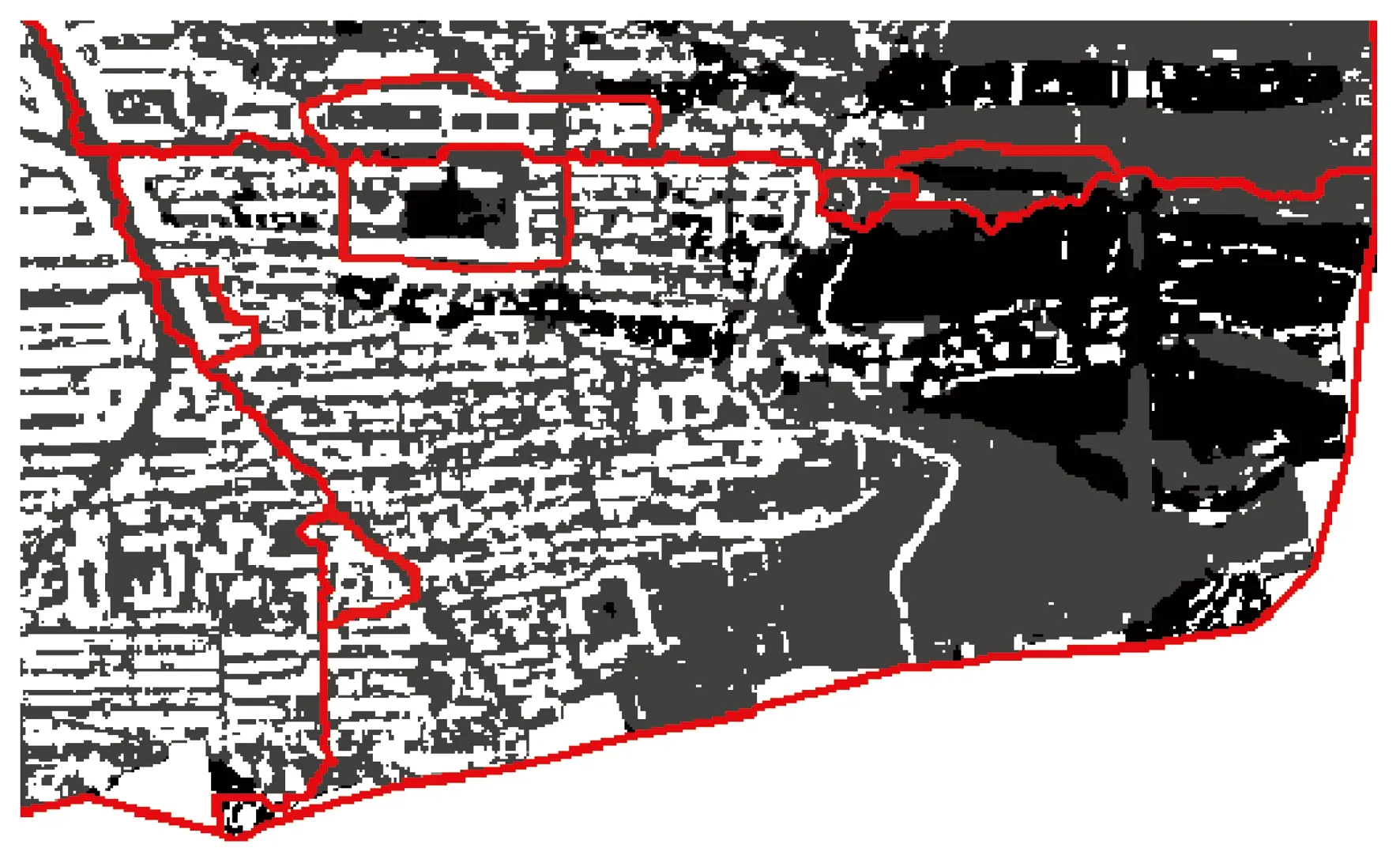
图4 接缝线多边形的局部放大结果Fig.4 Partial magnification of the seam line polygon

(1) 若两个相邻的接缝线多边形中,其中一个接缝线多边形是面积极大的多边形,而另一个相较而言是面积极小的多边形。若这两个接缝线多边形定位的单张正射影像相同,则在拼接数字正射影像图的过程中,由于这两个接缝线多边形选择同一张单张正射影像,在时间效率上就会多花一倍的时间进行数字正射影像图的拼接。因此,生成正射影像的效率就会大幅度降低。

(2) 若面积极大的接缝线多边形轮廓比定位的单张正射影像的面积大,那么在拼接后的数字正射影像图中就会出现空洞,直接影响生产的数字正射影像图的质量。

3.2 优化生成的接缝线多边形

(1) 基于定位影像的接缝线多边形优化 针对生成的接缝线多边形中出现面积极大或极小问题,根据接缝线多边形定位的单张正射影像Id对问题现象进行处理。整体思路是:首先将接缝线多边形定位到单张正射影像上;然后自定义面积为1 000(经验值)的接缝线多边形,将面积小于1 000的接缝线多边形查找出来。遍历小多边形数组,在大多边形数组中查找与小多边形有公共点的多边形,最后判断面积极小的接缝线多边形与相邻的大多边形公共点个数,若公共点个数大于2则合并,否则继续在大多边形数组中查找。基于定位影像的接缝线多边形优化流程如图5所示。

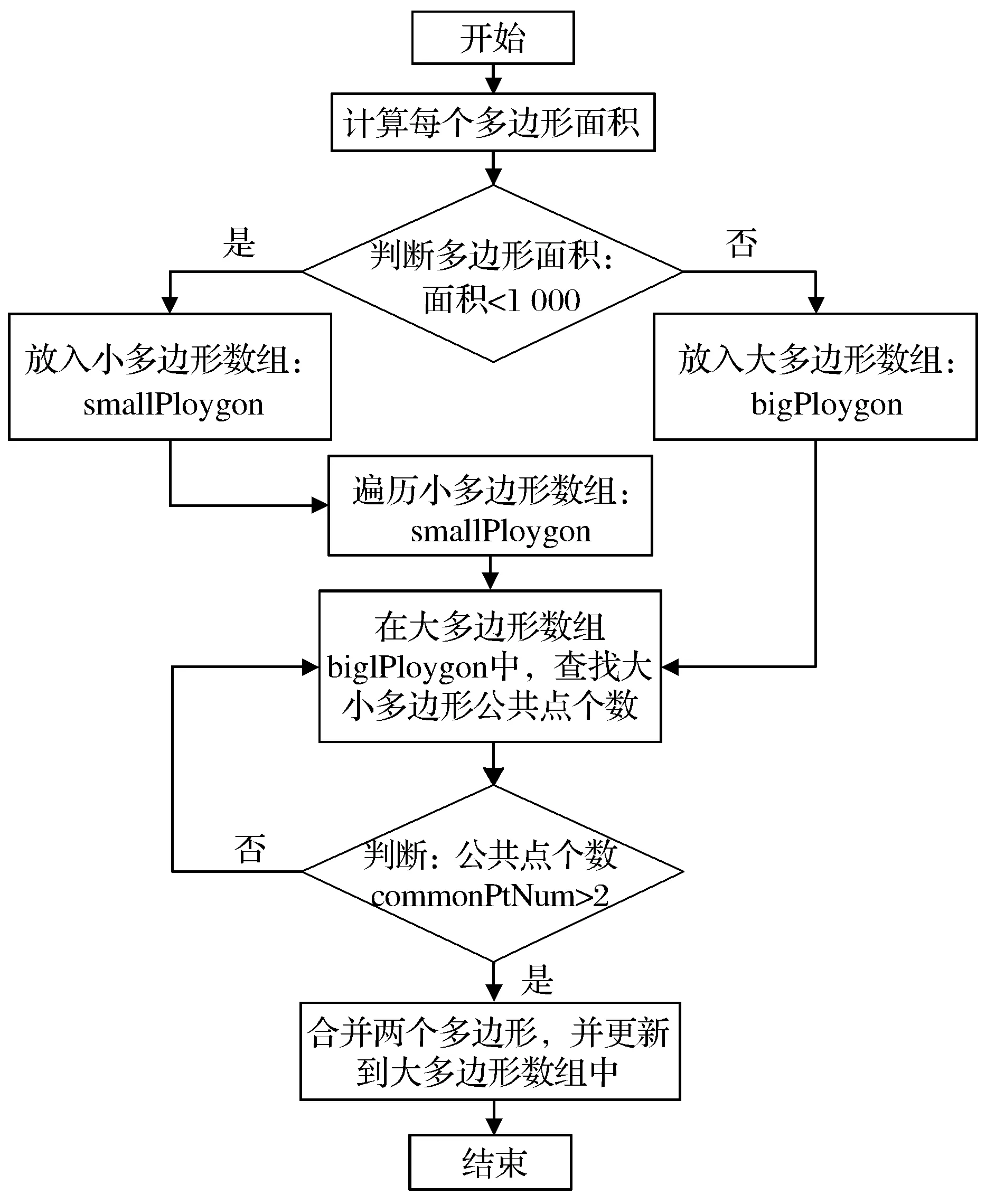
图5 基于定位影像的接缝线多边形优化流程Fig.5 Optimization flow chart of seam line polygonbased on positioning image

基于定位影像的接缝线多边形优化的详细步骤如下:

步骤1给每个接缝线多边形赋影像Id进行定位。赋值影像Id的方法是根据接缝线多边形与单张正射影像外轮廓求交,计算每个接缝线多边形的面积与所有单张正射影像外轮廓面积,若其中的一张影像与接缝线多边形相交的面积最大,将这张单张正射影像的Id赋值给此接缝线多边形。

步骤2自定义接缝线多边形阈值。计算每个接缝线多边形的面积,若此接缝线多边形的面积大于自定义的阈值,则将此接缝线多边形放入bigPolygon数组中。若此接缝线多边形的面积小于自定义的阈值,则将此接缝线多边形放入smallPolygon数组中。

步骤3将所有面积小的接缝线多边形逐一进行遍历,在面积大的接缝线多边形数组中查找出与面积小的多边形有两个以上公共交点的大多边形,如果这两个多边形所属的影像Id相同,可将面积大的多边形与面积小的多边形进行合并。

(2) 基于影像外轮廓的接缝线多边形优化 针对面积较大的接缝线多边形轮廓大于单张正射影像的外轮廓导致生成的数字正射影像图出现空洞现象,可根据三角网与定位的影像外轮廓解决此问题。整体思路是:将接缝线多边形定位的影像Id同时赋给三角网内属于接缝线多边形范围内的三角形。将没有赋值影像Id的三角形扩散生成一个多边形,此多边形作为一个新的接缝线多边形重新定位单张正射影像,并加入接缝线多边形数组。基于影像外轮廓的接缝线多边形优化流程如图6所示。

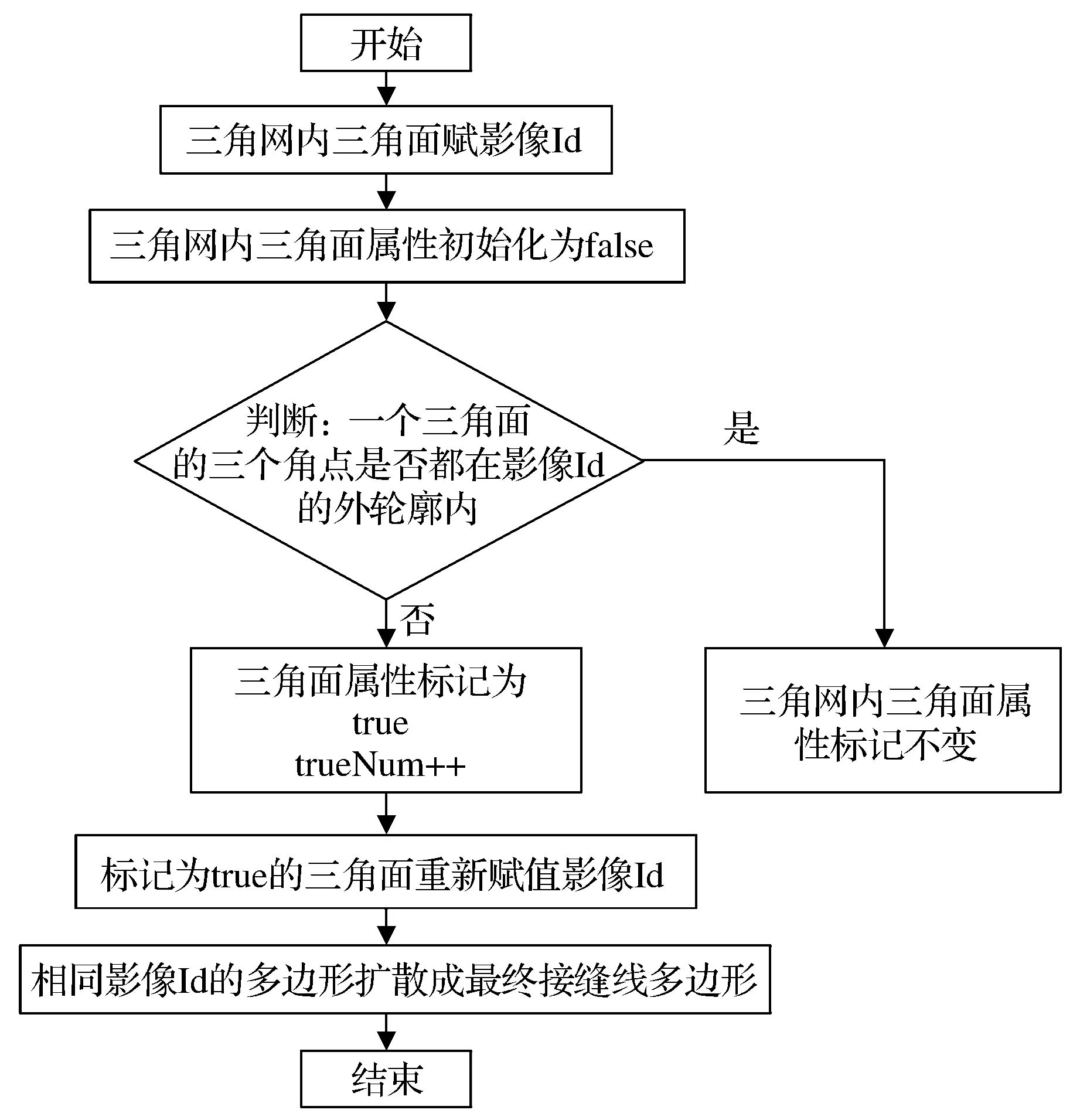
图6 基于影像外轮廓的接缝线多边形优化流程Fig.6 Optimization flow chart of seam line polygonbased on image outer contour

基于影像外轮廓的接缝线多边形优化的详细步骤如下:

步骤1利用可视化与计算机图形学库VCG Libary(visulization and computer graphics libary)计算出每个三角形的重心坐标。判断三角网中每个三角形的重心坐标位于哪个接缝线多边形,将接缝线多边形定位的影像Id赋值给三角形。

步骤2判断每个三角形是否处于所属的影像外轮廓范围内。首先将三角网中的面属性初始化为false。判断三角网中的每个三角面的面属性是否为false,若三角形的面属性为false,则判断三角形的三个角点坐标是否全部处于定位影像Id的轮廓范围内。若是,则将影像的Id赋值给此三角形。若否,则将三角形的面属性标记为true。迭代的终止条件是三角形属性为true的个数不再增加。

步骤3将三角网中三角形的面属性为true的三角形扩散成一个或多个多边形,放入临时的多边形数组中,并给临时数组中的所有多边形定位单张正射影像Id。

步骤4将临时数组中定位单张正射影像Id后的多边形添加到接缝线多边形数组中,此时接缝线多边形数组就是最终生成的接缝线多边形。

优化前与优化后的接缝线多边形局部放大结果对比如图7所示。

图7 优化前与优化后的接缝线多边形局部放大结果对比Fig.7 Comparison diagram of partial enlargement result of seam line polygon before and after optimization

基于定位影像的接缝线多边形优化和基于影像外轮廓的接缝线多边形优化后最终生成的接缝线多边形如图8 所示。

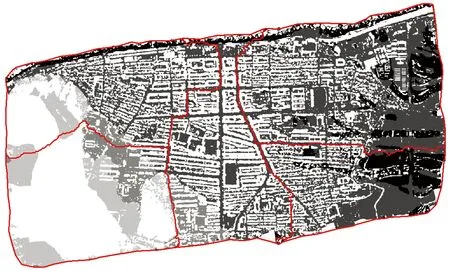
图8 最终生成的接缝线多边形Fig.8 The final result of seam line polygon

4 实验结果及分析

为验证本次算法在方法上的优越性以及可以获得高质量的实验结果,选取基于voronoi图生成的接缝线多边形和本次研究基于Dijkstra算法生成接缝线多边形进行对比。首先在主观视觉上对本次研究生成的接缝线进行直观判断和分析,然后通过客观的计算方法验证本次研究生成接缝线的结果。

4.1 实验数据

(1) 江西某测区 第一次实验选择的是丘陵地带,选取江西某测区进行无人机航空影像数据获取,并利用本次算法进行数据处理。江西某测区根据本次算法生成的接缝线生产出的数字正射影像图如图9所示。在测区范围内无人机拍摄的影像张数是4 712张,旁向重叠度和航向重叠度都符合测绘行业的要求。无人机在江西测区范围内的航拍数据如表1所列。

图9 江西影像数据生成的数字正射影像图Fig.9 Digital orthophoto map generated fromJiangxi image data

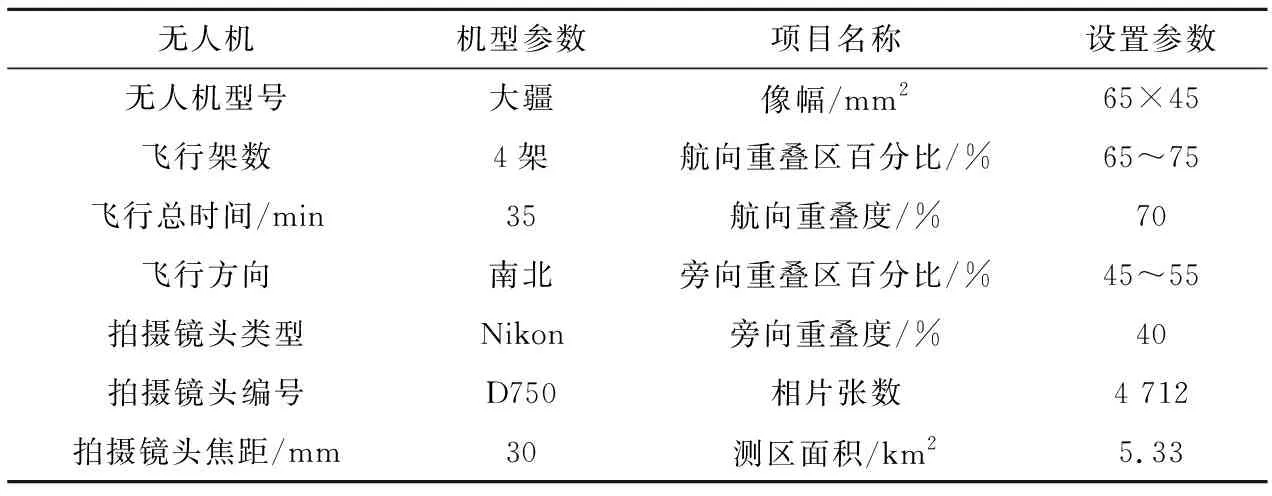
表1 江西某测区无人机航拍数据

(2) 武汉某测区 第二次实验选择了拥有密集建筑物的武汉某测区作为实验区进行本次算法的验证。武汉测区根据本次算法生成接缝线后生产出的数字正射影像图如图10所示。在测区范围内无人机拍摄的影像张数是10 531张,旁向重叠度和航向重叠度在很大程度上高于我国测绘行业的要求。无人机在武汉测区范围内的航拍数据如表2所列。

图10 武汉影像数据生成的数字正射影像图Fig.10 Digital orthophoto map generated fromWuhan image data

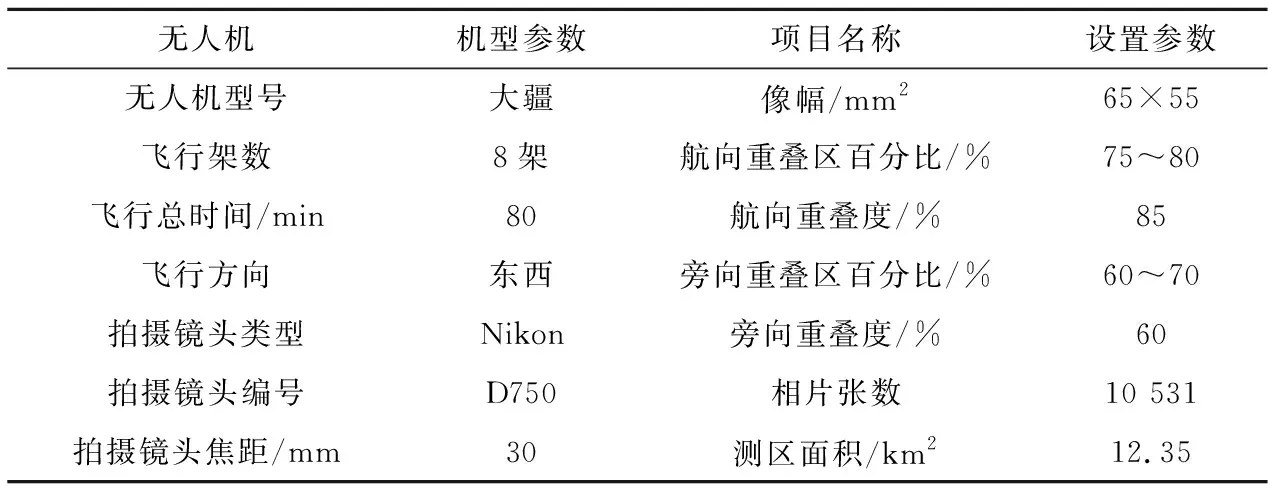
表2 武汉某测区无人机航拍数据

4.2 主观视觉评价

以主观评价方法对本次算法生成接缝线后生产的数字正射影像图的判断是一种简单、快捷、直观且有效的评价方法,可以快速判断出影像在质量上的效果。通过该评价方法可以直接判断出拼接后的数字正射影像图效果。江西和武汉某测区根据voronoi图算法及本次算法生成接缝线后生产的数字正射影像图局部放大处理结果如图11和图12所示。

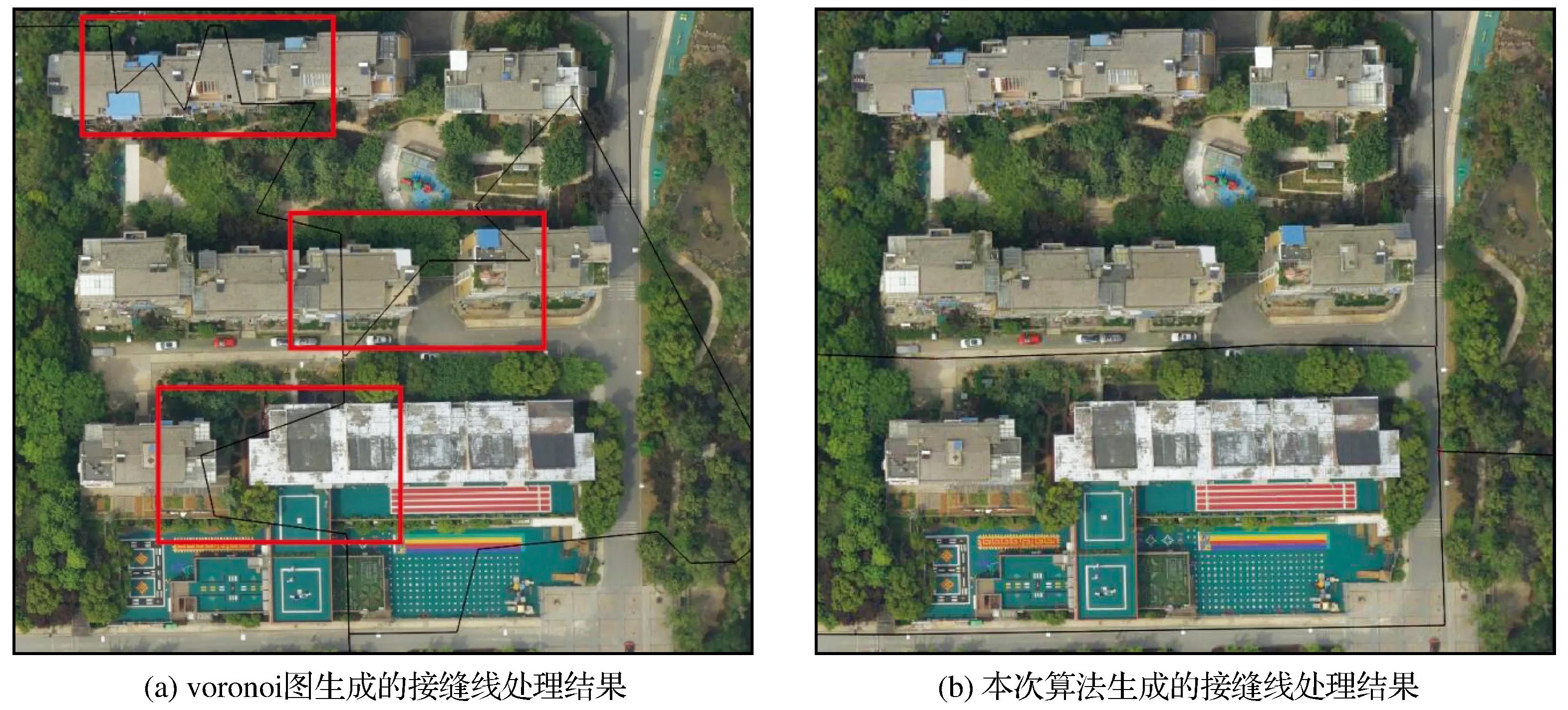
图11 江西某测区数字正射影像图局部处理结果Fig.11 Local processing results of digital orthophoto images in a certain area of Jiangxi

图12 武汉某测区数字正射影像图局部处理结果Fig.12 Local processing results of digital orthophoto images in a survey area in Wuhan

由图11和图12可以直观发现基于voronoi图算法生成的航空影像接缝线多边形比较杂乱,而本次算法生成的航空影像接缝线多边形较为规则。综上所述,通过主观视觉观察数字正射影像图的效果发现,本次算法生成的接缝线多边形最终生产的数字正射影像图效果优于voronoi图算法生产的数字正射影像图效果。

4.3 客观数据评价

为了从更严谨的角度证明由本次算法生成的接缝线多边形生产的数字正射影像图效果,分别计算本次算法和voronoi图算法生成的数字正射影像图中的像素灰度的平均值、像素灰度与均值的标准偏差、平均梯度,并对计算结果进行对比分析。

(1) 计算生成的数字正射影像图的像素灰度的平均值 通过这种方法分别计算出基于voronoi图算法和本次算法生成的数字正射影像图结果,可以客观说明拼接后的数字正射影像上整体视觉和成图质量效果,均值越大说明拼接效果越好。其计算公式为

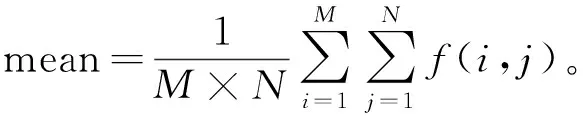
(1)

数字正射影像图灰度平均值如表3所列。由表3可知,江西测区和武汉测区拼接生成的数字正射影像图结果中本次算法效果最佳,其次是voronoi图算法生成的数字正射影像图结果。因此,相比voronoi图算法接缝线拼接的数字正射影像图,本次算法 生成的接缝线拼接的数字正射影像图的成图质量较好。

表3 生成的数字正射影像图灰度平均值比较

(2) 计算生成的数字正射影像图的平均梯度 计算数字正射影像图的平均梯度可以反映出影像上信息量与纹理变化特征。通过判断计算结果可知,计算的结果值越大,说明拼接生成的数字正射影像质量越好,并且可以证明数字正射影像图上纹理清晰,可得到的地理信息数据越多,平均梯度值越大说明拼接效果越好。其计算公式为

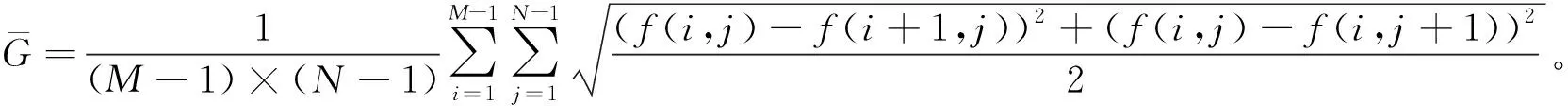
(2)

数字正射影像图平均梯度如表4所列。对比表4发现,江西测区和武汉测区拼接生成的数字正射影像图结果中本次算法最优,其次是voronoi图算法生成的数字正射影像图结果。与voronoi图算法结果相比,本次算法拼接的数字正射影像图纹理特征更加清晰,包含的信息量更加丰富。

表4 生成的数字正射影像图平均梯度比较

(3) voronoi算法和本次算法生成的数字正射影像图的时间效率比较 生成接缝线多边形的时间效率如表5所列。由表5可知,在时间上效率上本次算法大大优于voronoi图算法,实验数据证明了本次算法在时间效率上的优越性。

表5 生成接缝线多边形的时间效率比较

综上所述,对比两种方法得出的结果发现,在Dijkstra算法的基础上对三角网进行约束搜索,将搜索结果追踪生成接缝线多边形的方法生成的数字正射影像图,比voronoi图算法生成的数字正射影像图纹理更清晰,信息量更丰富,时间效率更快,完全满足成图质量要求。

5 结论

(1) 为了快速生产数字正射影像,研究提出一种顾及约束条件的Dijkstra算法生成接缝线多边形,并对接缝线多边形进行基于定位影像与影像外轮廓的优化,对DSM提取出的候选点利用Delaunary算法构建三角网并赋权值,对Dijkstra算法搜索最短路径的范围进行约束,提高了最短路径搜索效率。

(2) 针对生成的多边形出现的极大极小问题,提出基于定位影像的接缝线多边形优化与基于影像外轮廓的接缝线多边形优化方法。优化方法进一步提高了数字正射影像的生产效率,避免了拼接后的数字正射影像出现空洞。

(3) 将本次算法与voronoi图算法生成的接缝线多边形分别拼接生成数字正射影像图,通过主观视觉和客观数据对比分析发现,本次算法生成的接缝线多边形较为规则,影像质量较好,且在生成接缝线的时间效率上优于voronoi图算法。